一类广义非线性似变分不等式的辅助问题研究

高海燕

(1. 大连财经学院 基础教育学院，辽宁 大连 116622;2. 东北财经大学 数学与数量经济学院，辽宁 大连 116025)

0 引言

变分不等式理论是应用数学学科中一个非常重要的研究领域．它被广泛的应用于海洋学、弹性力学、控制论、非线性最优化、经济平衡理论、物理和工程科学等多种学科．变分不等式理论中最重要的问题之一是构造有效的迭代算法找出变分不等式的逼近解．文献[3-16]中介绍了多种逼近解的迭代算法．Glowinski, Lions和Tremolieres[8]引入了辅助原理技术，此后，Ding[3,4]，Ding和Tan[5]，Ding和Yao[6]，Gao等[7]， Liu等[9-12]，Zhang等[14]，Zeng 等[15]，Zeng等[16]，高[17]，以及很多学者都研究了不同的求解广义非线性变分不等式的逼近解的迭代算法．

受上述工作[3-16]的启发，本文研究了一类广义非线性似变分不等式，证明了此类广义非线性似变分不等式解的存在性，并利用Chang[1,2]的结论和辅助原理技术构造了一种新的逼近解的迭代算法，同时证明了这种算法的收敛性．文中的结果推广和改进了Ding[3]，Gao等[7]，Liu等[9]，Liu等[11]，Yao[13]，高[17]以及其他学者的相关结论．

1 预备知识

设H为实Hilbert空间，H*为其对偶空间，表示元素u∈H与v∈H之间的偶对．设K为H的非空闭凸子集．假设a:K×K→(-∞,+∞)为强制连续双线性型，即存在系数c,d>0满足：

(i)a(u,v)≥c‖v‖2,∀v∈K;

(ii)|a(u,v)|≤d‖u‖‖v‖,∀u.v∈K.

由(ⅰ)和(ⅱ)可以推知c≤d.

设b:K×K→(-∞,+∞)是不可微的并且满足以下条件：

(ⅲ)b(·,·)在第一变元是线性的;

(ⅳ)b(·,·)在第二变元是凸的;

(V)b(·,·)是有界的, 即存在系数l>0使得|b(u,v)|≤l‖u‖‖v‖,∀u.v∈K.

(ⅵ)b(u,v)→b(u,w)≤b(u,v-w),

∀u.v∈K.

考虑如下广义非线性似变分不等式(以下简称GNVLI):

对于给定的g∈H，求u∈K满足

〈N(Au,Bu,Cu)-g,η(v,u)〉+a(u,v-u)-b(u,u)+b(u,v)≥0,∀v∈K,

(1)

特殊情况

如果N(Au，Bu,Cu)=Au-Bu,g=0,

b(u,v)=f(v),∀u,v∈K,

其中f:H→(-∞,+∞)是一个函数, 那么GNVLI等价于求u∈K满足

〈Au-Bu,η(v,u)〉≥f(u)-f(v),∀v∈K.

(2)

详见 Ding[3]．

定义1 设映射A，B：K→H,N:H×H×H→H,η：K×K→H*.

(1) 称A为r-Lipschitz连续, 如果存在常数r>0满足

‖Au-Av‖≤r‖u-v‖,∀u,v∈K.

(3)

(2) 称N关于第一元A为s-η-强单调，如果存在常数s>0满足

〈N(Ax,u,v)-N(Ay,u,v),η(x,y)〉≥s‖x-y‖2,∀x,y∈K,∀u,v∈H.

(4)

(3) 称N关于第二元A为η-强单调，如果满足

〈N(u,Ax,v)-N(u,Ay,v),η(x,y)〉≥0,∀x,y∈K,∀u,v∈H.

(5)

(4) 称N关于第三元A为t-Lipschitz连续，如果存在常数t>0满足

‖N(u,v,x)-N(u,v,y)‖≤t‖x-y‖,∀x,y,u,v∈H.

(6)

(5) 称N关于第一元A和第二元B为η-半连续，如果满足对任意给定的x,y,z∈K映射g:[0,1]→(-∞,+∞)在0+连续，其中

g(t)=〈N(A(tx+(1-t)y),B(tx+(1-t)y,z),η(x,y)〉

(6) 称η为s-Lipschitz连续，如果存在常数s>0满足

‖η(u,v)‖≤s‖u-v‖,∀u,v∈K.

(7)

(7) 称η为t-强单调，如果存在常数t>0满足

≥t‖u-v‖2,∀u,v∈K.

(8)

引理1[1,2]设X是Hausdorff线性拓扑空间E的一个非空闭凸子集，如果两个映射φ,ψ:X×X→(-∞,+∞)满足如下条件：

(Ⅰ)ψ(x,y)≤φ(x,y),∀x,y∈X,并且ψ(x,x)≥0,∀x∈X；

(Ⅱ) 对每个x∈X,ψ(x,·)在X上是上半连续的；

(Ⅲ) 对每个y∈X,集合{x∈X:ψ(x,y)<0}是凸的；

(Ⅳ) 存在一个非空紧集K⊂X和元素x0∈K使得ψ(x0,y)<0,∀y∈XK,

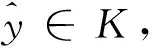
2 主要内容

首先考虑 GNVLI (1)的辅助问题．

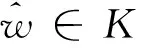
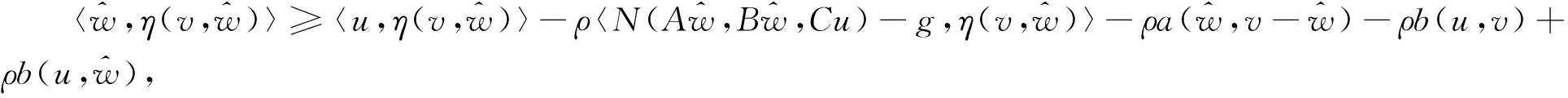
(9)

其中ρ>0是个常数．

定理1 设K是H的非空闭凸子集，并且g∈H．设a:K×K→(-∞,+∞)满足(ⅰ)，(ⅱ)，b:K×K→(-∞,+∞)满足(ⅲ)- (ⅵ) ，映射A,B,C:K→H，及N:H×H×H→H满足N关于第一元A和第二元B为η-半连续．设η:K×K→H*为δ-Lipschitz连续和τ-强单调的，对每个y∈K，η(·,K)连续且满足η(y,x)=-η(x,y),∀x,y∈K．假设N关于第一元A为α-η-强单调, 关于第二元B为η-强单调．如果对于给定的x,y,z∈H及v∈K，映射〈N(x,y,z),η(v,·)〉是凹的和上半连续的，则辅助问题(9)在K中有唯一解．

证明设u∈K．定义函数φ,Ψ：K×K→R如下：

φ(v,w)=〈v,η(v,w)〉-〈u,η(v,w)〉+ρ〈N(Av,Bv,Cu)-g,η(v,w)〉+ρa(v,v-w)-ρb(u,w)+ρb(u,v),∀v,w∈K

(10)

ψ(v,w)=〈w,η(v,w)〉-〈u,η(v,w)〉+ρ〈N(Aw,Bw,Cu)-g,η(v,w)〉+ρa(w,v-w)-ρb(u,w)+ρb(u,v),∀v,w∈K

(11)

先证明映射φ,ψ满足引理 1的条件．易证对任意的v,w∈K，有

φ(v,w)-ψ(v,w)=〈v-w,η(v,w)〉+ρ〈N(Av,Bv,Cu)-N(Aw,Bw,Cu),η(v,w)〉+ρ〈N(Aw,Bv,Cu)-N(Aw,Bw,Cu),η(v,w)〉+ρa(v-w,v-w)≥[τ+ρ(α+c)]‖v-w‖2≥0

(12)

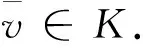
(13)

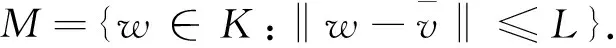
(14)

显然，M是K的弱紧子集，对任意的w∈KM，

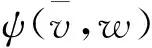
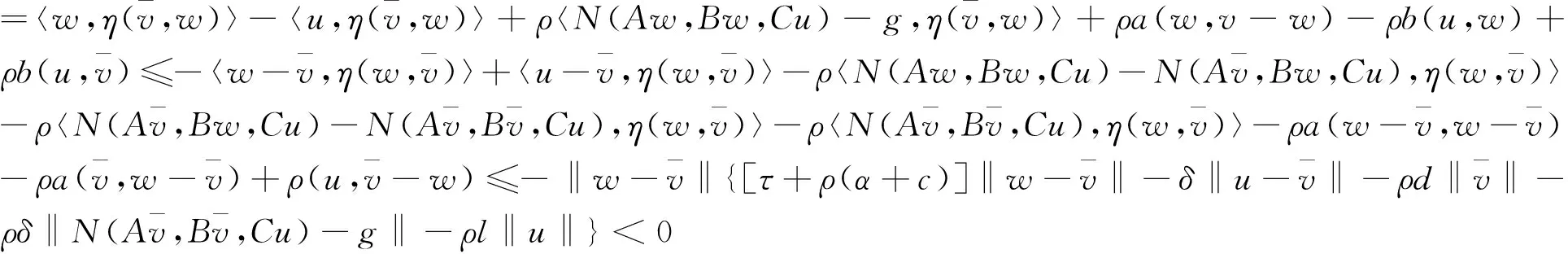
(15)

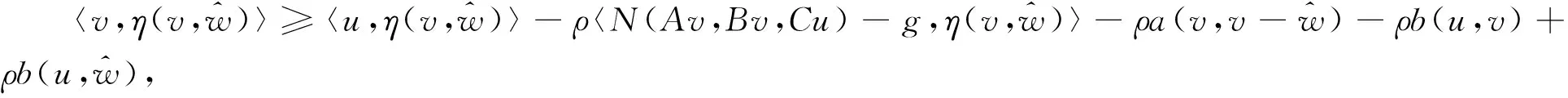
(16)

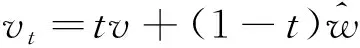
(17)

注意到b在第二变元是凸的，〈N(x,y,z),η(v,·)〉是凹的和上半连续的．由(ⅵ)和(17)推知

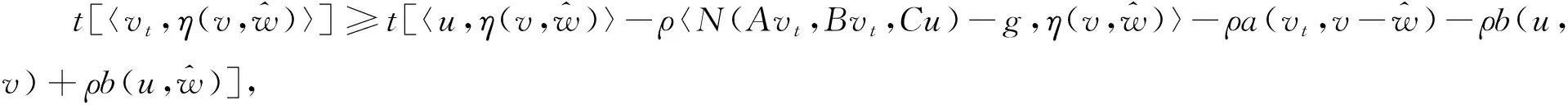
(18)

因此

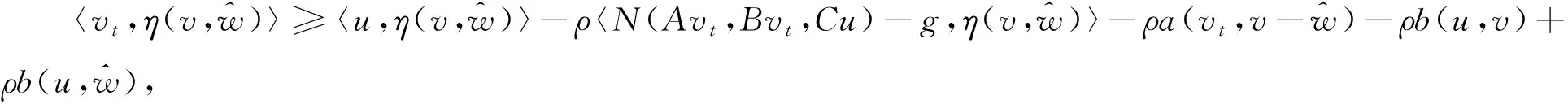
(19)

在以上不等式中令t→0+，可得

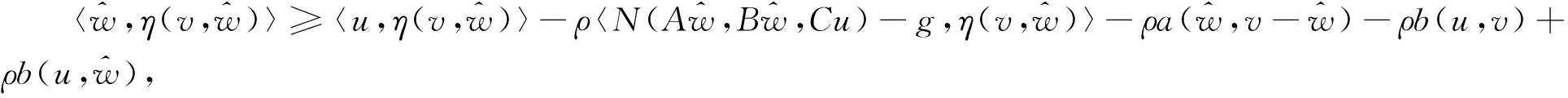
(20)

以下证明唯一性．设w1,w2∈K是(9)的两个解，则对任意的∀v∈K有

〈w1,η(v,w1)〉≥〈u,η(v,w1)〉-ρ〈N(Aw1,Bw1,Cu)-g,η(v,w1)〉-ρa(w1,v-w1)-ρb(u,v)+ρb(u,w1),

(21)

〈w2,η(v,w2)〉≥〈u,η(v,w2)〉-ρ〈N(Aw2,Bw2,Cu)-g,η(v,w2)〉-ρa(w2,v-w2)-ρb(u,v)+ρb(u,w2),(22)

分别取(21)中v=w2，(22)中v=w1，并将两个不等式相加可得

τ‖w1-w2‖2≤-ρ〈N(Aw1,Bw1,Cu)-N(Aw2,Bw1,Cu),η(w1,w2)〉-ρ〈N(Aw2,Bw1,Cu)-N(Aw2,Bw2,Cu),η(w1,w2)〉-ρα(w1-w2,w1-w2)≤-ρ(α+c)‖w1-w2‖2,

(23)

根据定理1, 构造以下逼近 GNVLI 的解的迭代算法．

迭代算法假设a:K×K→(-∞,+∞)满足(ⅰ)，(ⅱ)，b:K×K→(-∞,+∞)满足(ⅲ)- (ⅵ)，A,B,C:K→H,N:H×H×H→H，η:K×K→H*为映射．对给定的u0∈K，按如下算法计算序列{un}n≥0⊂K：

〈un+1,η(v,un+1)〉≥〈un,η(v,un+1)〉-ρ〈N(Aun+1,Bun+1,Cun)-g,η(v,un+1)〉-ρa(un+1,v-un+1)-ρb(un,un+1)+〈en,η(v,un+1)〉,∀v∈K,n≥0,

(24)

其中{en}n≥0⊂H，且ρ>0是常数．

其次, 考虑GNVLI解的存在唯一性, 以及由迭代算法产生的迭代序列的收敛性．

定理2 设a,b,A,B,N,η与定理1中相同，设C:K→H为ξ-Lipschitz连续，N关于第三元为σ-Lipschitz连续及关于第三元C为β-η-强单调，并且满足

(25)

如果存在一个常数ρ满足

(26)

和下列条件之一：

(27)

(28)

则GNVLI存在解u∈K，并且由迭代算法定义的迭代序列{un}n≥0强收敛到u．

证明根据定理 3.1的证明可知存在映射G:K→K满足G(u)=w,∀u∈K其中w是(9)的唯一解．下面证明G是一个压缩映射．设x1,x2,y是K中的任意元. 由(9)可得

〈Gx1,η(y,Gx1)〉≥〈x1,η(y,Gx1)〉-ρ〈N(A(Gx1),B(Gx1),Cx1)-g,η(y,Gx1)〉-ρa(Gx1,y-Gx1)-ρb(x1,y)+ρb(x1,Gx1),

(29)

〈Gx2,η(y,Gx2)〉≥〈x2,η(y,Gx2)〉-ρ〈N(A(Gx2),B(Gx2),Cx2)-g,η(y,Gx2)〉-ρa(Gx2,y-Gx2)-ρb(x2,y)+ρb(x2,Gx2),

(30)

分别取(29)中y=Gx2，(30)中y=Gx1，并将两个不等式相加可得

(31)

亦即

‖Gx1-Gx2‖≤θ‖x1-x2‖

(32)

其中

(33)

结合(26)和(27) (28)之一，得θ<1．故此，G:K→K是一个压缩映射且有唯一的不动点u∈K．根据(9)知

〈u,η(v,u)〉≥〈u,η(v,u)〉-ρ〈N(Au,Bu,Cu)-g,η(v,u)〉-ρa(u,v-u)-ρb(u,v)+ρb(u,u),∀v∈K.

(34)

即有

〈N(Au,Bu,Cu)-g,η(v,u)〉+a(u,v-u)-b(u,u)+b(u,v)≥0,∀v∈K,

(35)

由此证明了u是GNVLI的解．

下面证明由上述迭代算法产生的迭代序列的收敛性．分别取(34)中v=un+1，(24)中v=u，并将两个不等式相加可得

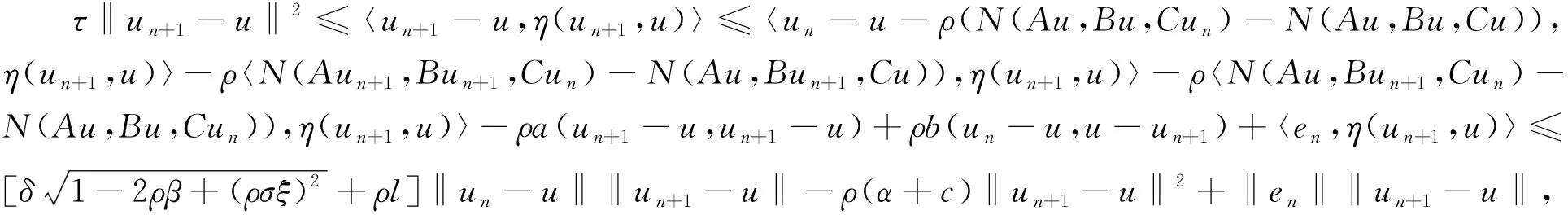
(36)

因此，

‖un+1-u‖≤θ‖un-u‖+‖en‖→0,n→∞

(37)

其中θ与(33)中相同．结合(25)和(37)可以推知，由上述迭代算法产生的迭代序列{un}n≥0强收敛到u．证毕．

注记 定理1和定理2推广和改进了文献[3,7,9,11,13]，和文献[17]中的相关结果．