正五边形尺规作图方法赏析
江苏省扬州市田家炳实验中学 谢俊峰
尺规作图是起源于古希腊的数学课题。历史上最先明确提出尺规限制的是希腊天文学家、数学家伊诺皮迪斯。由于对尺规作图的限制,使得一些貌似简单的几何作图问题无法解决。最著名的是古希腊最有影响力的四大数学学派之一——巧辨学派提出的三大著名尺规作图问题:倍立方问题、化圆为方问题、三等分角,当然,这三个问题都已被证明不可能用尺规作图来解决。
尺规作图中有许多有趣的问题,其中作正多边形就是其中一种。大家认为这是一个简单的问题,但在操作中我们知道,正四边形、正五边形、正六边形都比较简单,但到正七边形、正九边形却遇到了很大的困难,最终解决这个问题的是伟大的数学家高斯,他给出了可用尺规作图的正多边形的条件:尺规作图正多边形的边数目必须是2的非负整数次方和不同的费马素数的积。本文提供正五边形的几种作图方法,供大家赏析。
一、已知圆的半径为r,求作圆的内接正五边形
作法1:如图1,作圆O的任意半径OA1,A1B⊥OA1,并使得连接BO,以B为圆心,BA1为半径作弧截BO于点C,以O为圆心、OC为半径作弧截OA1于点M,以点A1起顺次截取等于OM的弦A1A2,A2A3,…,A10A1,将A2、A4、A6、A8、A10顺次连接,即为圆的内接正五边形。

图1
作法2:如图2,作互相垂直的直径AM,BN,作ON的垂直平分线交ON于点E,以E为圆心、EA为半径作弧交OB于点F,从点A起顺次在圆上截取等于AF的弦,AA1、A1A2、A2A3、A3A4、A4A,顺次连接A、A1、A2、A3、A4、A,即得到正五边形。

图2

图3
作法3:如图3,任作圆O的半径OA1,过O点作OA1的垂线OB交圆O于点B,取OB的中点C,作∠OCA1的角平分线CD交于点D,过D点作DA2⊥OA1交圆O于点A2,从点A2起顺次在圆上截取等于 A1A2的弦 A2A3、A3A4、A4A5,顺次连接 A1、A2、A3、A4、A5、A,即得到正五边形。
二、已知正五边形边长为a,求作正五边形
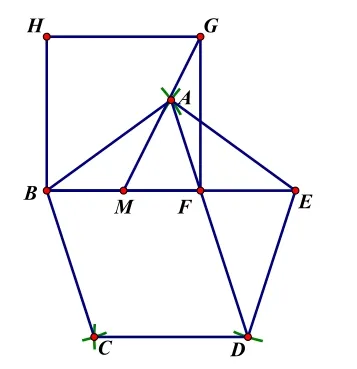
图4
作法2:作边长为a的正方形BFGH,取底边的中点M,然后与右上角顶点G连线;延长底边BF到E,使BE=BM+MG;分别以B、E为圆心,a为半径画弧,两弧在BE上方交于点A;连接AF并延长与以E为圆心,a为半径的圆交于点D;以D、B为圆心,a为半径画弧,两弧交于点C。依次连接A、B、C、D、E,即为所求的边长为a的正五边形。
三、已知正五边形对角线为m,求作正五边形
作法1:如图5,作任意圆O的内接正五边形A1A2A3A4A5,连接A1A4,在A1A4延长线上截取A1A'4=m,过点A'4作A'4A'3∥A4A3,A'4A'5∥A4A5,过点A'3作A'3A'2∥A3A2,则 A1A'2A'3A'4A'5为所作正五边形。
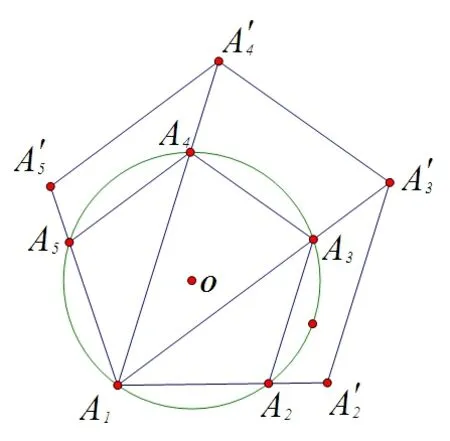
图5
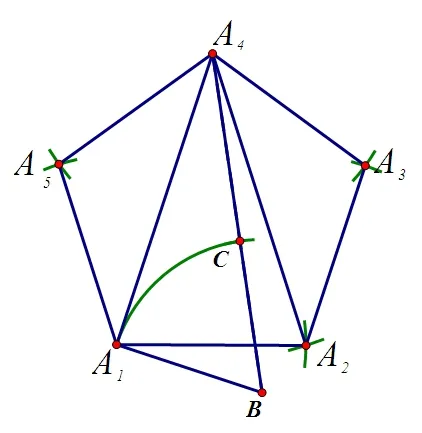
图6
作法2:如图6,作线段A1A4=m,作,使得连接A4B,以B为圆心,BA1为半径作圆,交A4B于点C,以A1为圆心,A4C为半径作弧,与以A4为圆心,A1A4为半径的弧交于点A2,分别以A1A4为圆心,A4C为半径作弧,交于点A5,以A2、A4为圆心,A4C为半径作弧,交于点A3,依次连接A1、A2、A3、A4、A5,则A1A2A3A4A5为所求正五边形。
上面介绍了正五边形的几种作图方法,大家可以继续去探究其他的作图方法并进行证明。正五边形还有一些近似作法,大家也可以去进一步探索。

