数学理解的基础:了解“是什么”
刘开来


似乎从懂事起,数学就伴随在我们的左右.虽然,很多人不太喜欢数学,只觉得它抽象难懂、枯燥乏味,但是,不论大家再怎么不喜欢,它都会一直忠心地陪伴我们成长.在学校里,我们学习数学的时间最多,并且如果课上讲的内容理解不够,课后还得花大量时间去苦思冥想、艰难探索;回到家里,家长关心我们时也总会问“老师讲的数学理解吗?”“理解数学”成为我们数学学习首要任务.笔者作为一名高三学生,正经历着高考的一轮复习,深感核心概念的理解的重要性:我们要理解数学,首先要了解其中核心概念“是什么”.本文拟以《解三角形》《数列》中三组核心概念为例,分别探索其本质.
一、正弦定理和余弦定理的本质
新课时,我们先通过对直角三角形边角关系的归纳,得出直角三角形边长与角度的一种关系,进而经历探索、猜想、发现并证明了正弦定理;通过向量的数量积将向量等式化为数量等式,得到余弦定理.
老师这样处理促进了我们对正弦定理和余弦定理的“数学理解”,有利于提升我们的归纳、猜想能力,体会向量方法在解三角形中的作用,学习完这部分内容后,我们对这两个定理的本质还可以认识得更深刻些:
两个定理均是关于边角的等式.
本题其实还是一类典型问题:已知两边和其中一边的对角,如何判断三角形解的个数?
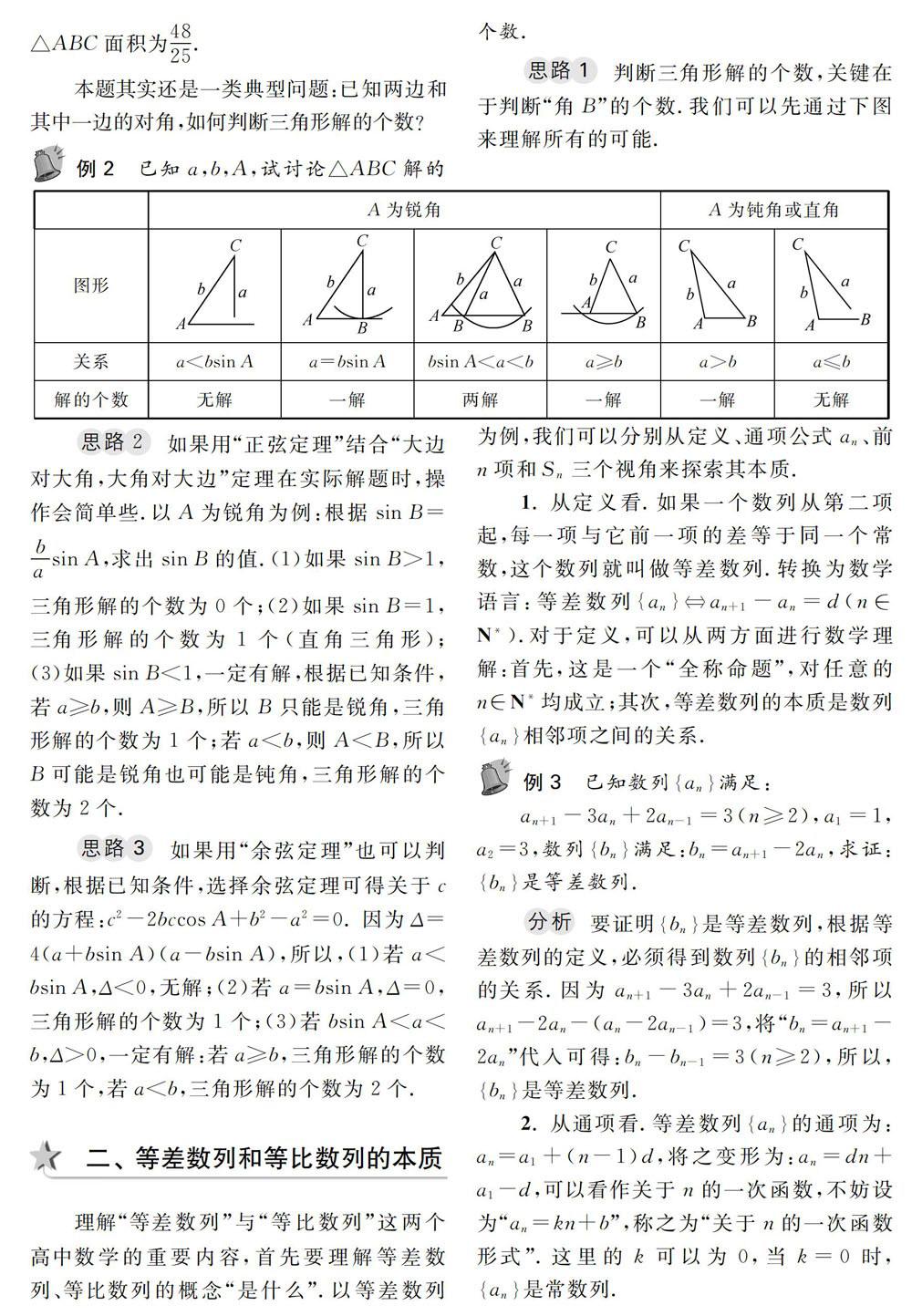
例2 已知a,b,A,试讨论△ABC解的个数.
思路1 判断三角形解的个数,关键在于判断“角B”的个数.我们可以先通过下图来理解所有的可能.
思路2 如果用“正弦定理”結合“大边对大角,大角对大边”定理在实际解题时,操作会简单些.以A为锐角为例:根据sin B=b/asin A,求出: sin B的值.(1)如果sin B>l,三角形解的个数为0个;(2)如果sin B=l,三角形解的个数为1个(直角三角形);(3)如果sin B 二、等差数列和等比数列的本质 理解“等差数列”与“等比数列”这两个高中数学的重要内容,首先要理解等差数列、等比数列的概念“是什么”.以等差数列为例,我们可以分别从定义、通项公式an、前n项和Sn

