对称性在数学教学中的应用

宁夏中卫市第一中学 李 伟

在数学教学中利用数学问题的对称性不仅有助于找到简洁优美的解法，也有利于学生思维水平的提高。更重要的是可以在学习数学的同时欣赏数学美，正如古代哲学家普洛克拉斯曾说：“哪里有数学，哪里就有美。”而对称美是数学美的基本内容和重要体现，因此在数学教学中，教师要有意识地揭示数学中的对称美，培养学生的美感，利用对称性提高学生解决问题的能力。

本文以例题为主，主要论述对称性在函数，几何等方面的应用，让学生充分认识对称性的作用，认识对称美。运用对称性可以锻炼学生的思维，拓展学生的视野，丰富学生的想象，提高学习效果。

一、对称的概念

“对称”一词，译自希腊语，其含义是“和谐”“美观”，原义指“在一些物品的布置时出现的般配与和谐”。我国老一辈数学家段学复教授也说过：“对称，照字面来讲，就是两个东西相对而又相称(或者说相仿、相等)。因此，把这两个东西互换一下，好像没动一样。”在现实世界中，形式上和内容上的对称性，广泛地存在于客观事物之中，既有轴对称、中心对称、镜面对称等等的空间对称，又有周期、节奏和旋律的时间对称。对称美，作为数学美的主要表现形式之一，其数学的实质就是自然物的和谐性在量和量的关系上最直观的表现，是组元的一个构形在其自同构变换群作用下具有的不变性。从狭义上说，对称是指通常意义下的几何对称和代数对称；从广义上讲，对称还包含对偶、匀称等方面的内容，及各种数学概念、公式、定理间的对称思想。

二、函数中的对称性问题

1.函数自身的对称性。

（1）利用奇偶函数的对称性解题。

众所周知，奇函数的图像关于原点对称，偶函数的图像关于y轴对称，只要掌握这些知识的内涵，就能得到处理这些问题的思路把看似复杂的问题简单化。

例1设（fx）是R上的奇函数，且（fx+3）=-（fx），当0≤时 （fx）=x，求（f2008）。

解：因为y=（fx）是定义在R上的奇函数，所以点（0，0）是其对称中心，又（fx+3）=-（fx）=（f-x）=（f0-x），所以直线是y=（fx）的对称轴，故y=（fx）是周期为6的周期函数，所以 （f2008）=（f6×335-2）=f（-2）=-（f3-1）=（f-1）=-（f1）=-1。

此题的关键是利用奇函数的重要性质（f-x）=-（fx）以及关于原点（0，0）对称，及函数（fx）的对称轴

（2）利用点的对称性解题。

例2（fx）是定义在R上的增函数，记F（x）=（fx）-（fk-x），求证：y=F（x）的图像关于点（a，0）对称的充要条件是k=2a。

证明充分性，只须证 F（2a-x）=-F（x），因为k=2a，所以F（2a-x）=（f2a-x）-（fx）=-[f（x）-f（2a-x）]=-F（x），所 以 y=F（x）关于点（a，0）对称。

必要性，因为 y=F（x）关于点（a，0）对称，所以 F（2a-x）=-F（x），即 f（2a-x）-f（k-2a+x）=（fk-x）-f（x），下面对k进行讨论。

① 当 k＞2a 时 f（2a-x）-f（k-2a+x）＜（fk-x）-（fx）。

②当k＜2a时 （f2a-x）-（fk-2a+x）＞（fk-x）-（fx）。

③当k=2a时等式成立。

（3）不同函数及图像之间的对称性。

例3设定义域为R的函数y=（fx）与 y=g（x）都有反函数并且 f（x-1）和g-（1x-2）函数的图像关于直线y=x对称，若g（5）=2007，求 （f4）。

解：因为函数y=（fx-1）和y=g-（1x-2）的图像关于直线y=x对称，所以y=g-1（x-2）的反函数是 y=f（x-1），而 y=g-1（x-2）的反函数是y=2+g（x），所以 （fx-1）=2+g（x），所以 （f5-1）=2+g（5）=2009，即（f4）=2009。

三、轮换对称式的应用

所谓轮换对称式即为：对于一个n元多项式 p（x1，x2…，xn）把它的 n 个变元顺次进行调换。如果这样得到的结果仍与原式相同，即 p（x1，x2…，xn）=p（x2，x3…xn，x1）那么这个多项式叫做关于这些变元的轮换对称式，简称轮换对称式，利用轮换对称式可使解题简洁优美。举例如下：

例 4 已知 α，β，γ，θ均为锐角，且α+β+γ+θ=π，求函数 y=sinαsinβsinγsinθ的最大值。

解：y=sinαsinβsinγsinθ

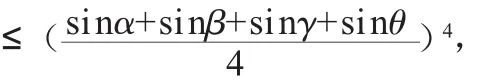
当且仅当 sinα=sinβ=sinγ=sinθ，

不论在自然界里还是建筑中，不论在艺术还是科学中，甚至最普通的生活用品中，中学数学中对称的形式随处可见。人类在漫长的岁月里，体验着对称，享受着对称。所以对称思想方法应该在《初中课标》和《高中课标》中给予提出，因为这一思想是贯穿小学数学、中学数学直到整个数学学科的一个永恒的概念。其实不仅在数学中，在宇宙万物中对称都是一个至简至深的概念，它是美的基本元素之一。但我相信数学是最能理解对称本质的一门学科。因此，在日常的数学教学中，要循序渐进地引导学生欣赏数学中的对称美，掌握数学中的对称思想，从而创新性地去应用数学中的对称思想[5]。通过对数学对称美的揭示，加强数学审美教育，使学生对数学产生一种积极而强烈的认识情绪，激发和增强学生的数学学习兴趣，使学生的情感受到陶冶，意志得到锻炼，从而对学习动机起到强化作用。