数学核心素养视角下问题情境的实验研究
——从“将军饮马”说开去
☉山东省高青县实验中学 王彩霞
数学中的“问题情境”,是一种以激发学生问题意识为价值取向的数据材料和情境信息,是从事数学活动、产生数学行为的条件.核心素养的数学教学理念不仅关注知识本身,还关注知识的文化背景和学生的应用迁移能力.在这种要求下,教师要善于设置问题情境,从生活实际入手,引导学生动手实践,提高学生的实际运用和思考能力,使学生的数学能力得到有效提升.下面笔者以“将军饮马”为问题情境,结合求线段和的最小值的教学,谈谈如何从问题情境出发,由问题情境展开,让问题情境贯穿始终,一个背景,一气呵成,一根主线,一以贯之,直抵教学的全部目标.
一、创设情境
著名的“将军饮马”问题:如图1,有一位将军骑着马要从A地走到B地,但途中要到河边饮马,则将军怎样走才能使总路程最短?

图1
二、建立模型
我们把河岸看成一条直线,转化成数学问题就是:如图2,点A、点B是直线l同旁的两个定点,在直线l上确定一点C,使CA+CB的值最小.联系前面学过的线段公理思考这个数学问题怎样解决.
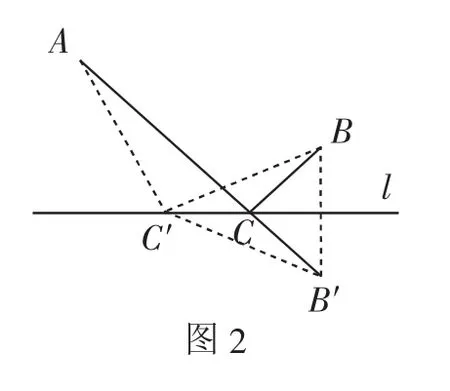
如果A、B两点在直线l的两旁,就可以直接利用两点之间线段最短来解决.怎样把A、B两点转化到直线l的两旁呢?利用轴对称的知识,点B关于直线l的对称点是B′,连接AB′交直线l于点C.连接BC.线段AC、BC就是将军走的最短路线.这样两点在直线同侧的问题就转化成了两点在直线异侧的问题.为什么说这个点C就使CA+CB的值最小呢?
为了证明这个问题,我们不妨在直线l上另外任取一点C′,连接AC′、BC′.
由直线l是线段BB′的对称轴,得CB=CB′,C′B=C′B′.
则AC+CB=AC+CB′=AB′.
在△AC′B′中,AB′<AC′+C′B′,则AC+CB<AC′+C′B.
即AC+CB最小.
所以AC、BC就是将军行走的路线,这时所走路程最短.
由此可见,求线段和的最小值的方法就是,找到两点一线模型,然后通过轴对称把在直线同侧的两点转化到直线的两侧,然后利用“两点之间,线段最短”,使问题迎刃而解.这就是“两定一动型”的最值问题.
三、拓展模型
数学来源于生活,又服务于生活.数学课程标准把培养和发展学生的应用意识作为基本的理念之一.两点一线模型还可以进行以下拓展,帮助我们解决生活中的实际问题.
1.一定两动型
如图3,将军骑马从军营A出发,先骑马去草地OX边吃草,再牵马去河边OY处饮水,最后回到军营,问:这位将军怎样走路程最短?

解析:如图3,利用轴对称的知识把点A转化到直线OX、OY的两侧,类比两点一线模型用线段公理就可以解决了.图中PA+PQ+QA就是将军所走的最短路线.
变式:如图4,将军骑马从军营A出发,先骑马去草地OM边吃草,再牵马去河边ON外饮水,最后将马送入河边上的马厩C,试确定马厩C的位置,使将军行走的路程最短.
解析:该问题即为:在∠MON的内部有一点A,在OM上找一点B,在ON上找一点C,使得AB+BC最短.先“化折为直”,作点A关于OM的对称点A′,然后解决如何使A′C最短的问题,即问题转化为确定射线ON外一点A′到ON的距离的最小值.显然,可根据“垂线段最短”的性质,确定马厩C的位置.
两题的理论依据是不同的,前者利用两点之间线段最短来求解的,而后者则依据垂线段最短.
2.两定两动型
(1)两线相交
如图5,A为马厩,B为帐篷,将军要从马厩牵出马,先到草地边的某一处牧马,再到河边饮水,然后回到帐篷,请你帮他确定出最短路线.
解析:作出点A关于草地的对称点A′,点B关于河的的对称点B′,类比两点一线模型用线段公理求解.如图5所示,AC—CD—DB即为最短路线.

(2)两线平行
如图6,将军从军营A出发去河边l处饮马,之后牵马沿河岸散步200米,再回军营B,问:从河边何处开始散步,可使整个行程最短?
解析:军营A与军营B是两个定点,问题即为:在直线l上找两个点C、D,CD=200米,使得AC+BD最短.若作点A关于l的对称点A′,连接A′C和BD,会出现两线段不共线的问题,怎么办?我们能不能把BD进行相应的平移,使得与A′C共线?
完全可以把BD沿着DC方向向左平移200米,问题迎刃而解.如图6,作点A关于l的对称点A′,将点B向左平移CD的长度到点B′(实际上为200米),连接A′B′,交直线l于点C,将点C向右平移CD的长度到点D,则点C、点D即为所求.
变式1:如图7,将军每日骑马从军营出发,去河岸对侧的 望台观察敌情,已知河两岸a、b平行,河流的宽度为30米,请问:在何地修浮桥,可使得将军每日的行程最短?
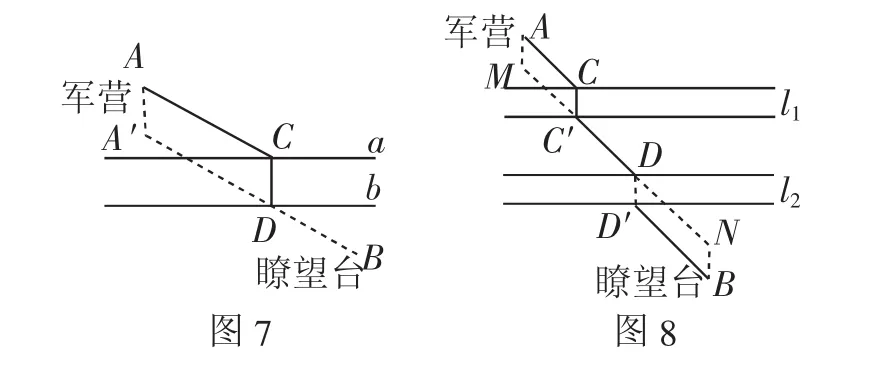
解析:这是著名的造桥选址问题.如图7,由于桥长CD是一个定值,故我们不妨将桥CD平移转化成两点一线的模型.无论桥架在何处,桥CD是必经路线,要使从A到B的折线最短,只需AC+BD最短即可.于是作AA′⊥直线a,且使AA′的长度等于河宽,连接A′B,交河岸b于点D,作DC⊥河岸a于点C,则建桥CD,可使得将军每日的行程最短.
这个造桥选址问题在教材中的原题是:“村庄A、B位于一条小河的两侧,若河岸a、b彼此平行,现在要建设一座与河岸垂直的桥,问:桥址应如何选择,才能使A村到B村的路程最近?”实际上两题是一样的,何不对教材进行重组与创新,使之处于一个情境之下?
变式2:如图8,军营A与瞭望台B之间隔着两条河,假定两条河互相平行并且河的两岸笔直,现在要在每条河上垂直于河岸分别建一座桥.应把桥建在什么位置,才能使将军走的路程最短?
解析:如图8所示,分别作AM垂直l1的河岸,BN垂直l2的河岸,且使AM的长度等于河l1的宽度,BN的长度等于河l2的宽度,连接MN,分别交两条河一侧于点C′、D,建桥CC′和DD′,连接AC、BD′,那么AC、CC′、C′D、DD′、D′B就是从军营A经过这两座桥到瞭望台的路程,此时路程最短.
这里无论涉及沿河边散步还是造桥选址问题,都用到了一个平移的思想方法,有的是“水平平移”,有的是“垂直平移”,当然还有“斜平移”,关键是抓住定长线段提供的平移方向与平移距离,进行相应的平移之后,即可转化为“两定一动型”常规最值问题,然后结合“两点之间,线段最短”的性质求解.显而易见,求线段和的最小值的教学,建立两点一线模型,可使问题得以解决.以“将军饮马”为问题情境,不是可以实现“从问题情境出发,由问题情境展开,让问题情境贯穿始终”的效果吗?反思一下,相比以“将军饮马”为主线,而用平面图形(比如:正方形、圆中求线段和的最小值)、立体图形、平面直角坐标系、二次函数或打台球等材料背景烘托,用一个背景,一气呵成,一根主线,一以贯之,直抵教学的全部目标,不是更有深意吗?相比将比较零散、看似不关联的几个材料进行不同的变式,用一个材料更能很好地体现它们密切相关,是一个模型的不同侧面,从而找到它们的异同点,不人为割裂,从而回归自然.结合以上两点一线模型的建构过程,把用数学模型解决实际问题的一般步骤概括如下,供大家参考.

图9

