靠船下篙，顺水推舟，船行千里——对2018年南通市中考数学第28题的分析与思考

☉江苏省如皋经济技术开发区实验初中 章小健

今年我有幸参加了2018年南通市中考数学试卷的评阅工作.今年数学试卷以“课标”为依据，以“教材”为题源，充分体现了“遵循课标，紧扣课本，重视能力，贴近生活，控制难度”五大命题原则.第28题（压轴题）以教材“最短路径模型”构造新定义，考查对定义的理解、运用和探究，试题入口熟悉又宽敞，解法多样，探索性强，是课本经典题目和题型的升华，让经典题有了新意，更有活力.

本文拟对第28题进行深入分析，并结合试卷中所反馈的信息，谈谈对数学教学的启示与思考.

一、试题呈现

【定义】如图1，A、B为直线l同侧的两点，过点A作直线l的对称点A′，连接A′B交直线l于点P.连接AP，则称点P为点A、B关于直线l的“等角点”.

（2）若直线l垂直于x轴，点P（m，n）是点A、B关于直线l的等角点，其中m＞2，∠APB=α，求证：tan

（3）若点P是点A、B关于直线y=ax+b（a≠0）的等角点，且点P位于直线AB的右下方，当∠APB=60°时，求b的取值范围（直接写出结果）.

二、参考答案

（1）C.

（2）如图3，因为点P（m，n）是点A、B关于直线l（直线x=m）的等角点，由定义可知A、A′关于直线x=m对称，所以PA=PA′，∠APG=∠BPH.

所以∠A=∠A′.又∠APB=∠A+∠A′=α，所以∠A=

作BH⊥直线x=m，垂足为H.

可得∠AGP=∠BHP=90°，所以△AGP △BHP，则

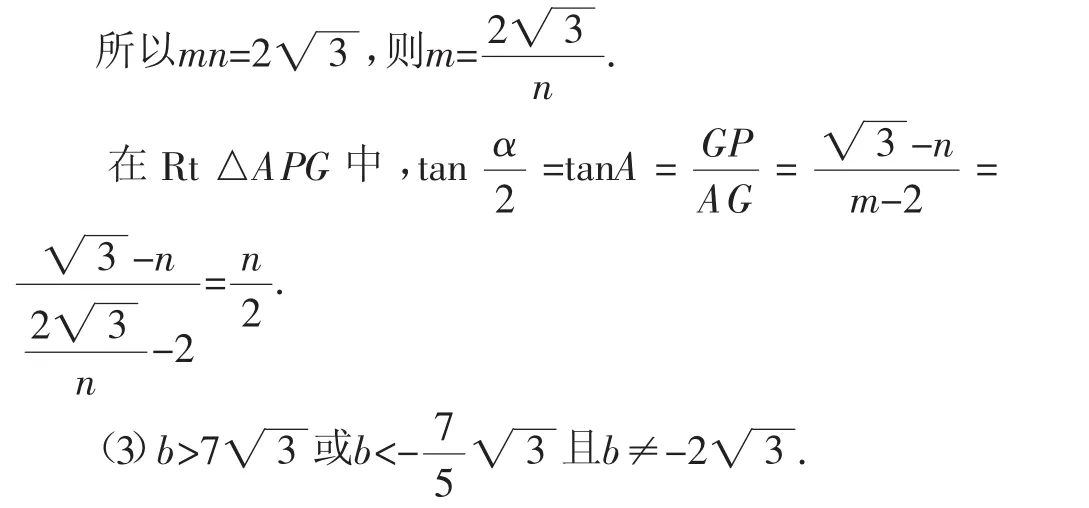
三、优秀解法

本题第（2）问，叙述简约，呈现简洁，解法灵活多样，现给出不同于参考答案的一些解法，供参考.

解法1：如图4，延长A′A交y轴于点G.设A′B交y轴于点H，连接GH.

因为点P（m，n）是点A、B关于直线（l直线x=m）的等角点，由定义可知A、A′关于直线x=m对称，可求得A（′2m-2，），PA=PA′，所以∠PAA′=∠A′.又∠APB=∠PAA′+∠A′=α，所以∠A

设直线A′B的解析式为y=kx+b（k≠0）.把A（′2m-2，）、B（-2，-）代入，得：

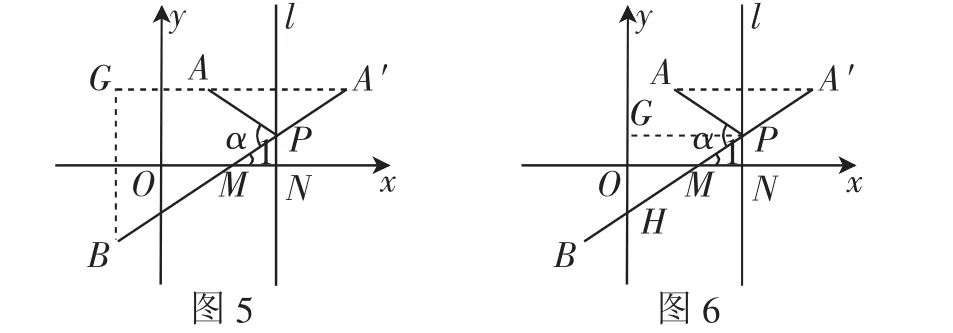
解法2：如图6，作PG⊥y轴于点G.设直线A′B交y轴于点H，则∠GPH=∠A′.

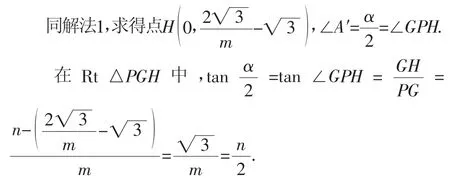
分析：解法1和解法2中，学生利用点的坐标求出了带参数的直线解析式，再利用直线的解析式求出与坐标轴的交点的坐标，利用坐标表示出线段的长度（用含m或n的代数式表示），从而在直角三角形中，利用三角函数的定义求解.此方法学生易下手，贴近学生思维.

解法3：如图7，设A′B交x轴于点M，直线x=m交x轴于点N，连接MN.

yA′+yB=0，所以A′、B关于点M对称.

由中点坐标公式，求得xM=m-2，所以MN=2.

分析：学生紧靠定义实现条件的转化，求出点A′的坐标，发现B、A′关于点M对称，从而求出M点的坐标，进而求出MN的长，根据要证结论，考虑包含的直角三角形，直接利用定义转化成线段的比值，问题得证.解法独特，颇具新意.

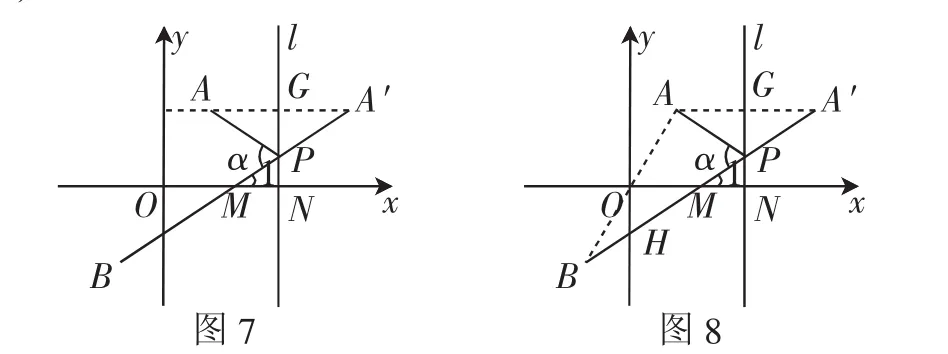
解法4：如图8，连接AB.

yA′+yB=0，所以A′、B关于点M对称.

O、M分别是BA、BA′的中点，所以OM是△BAA′的中位线.

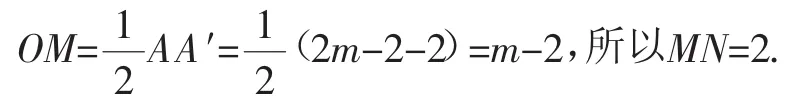
解法5：如图9，过A′、B分别作x轴和y轴的垂线，交于点H，A′H交x轴于点N.

yA′+yB=0，所以A′、B关于点M对称，M是BA′的中点.又N为AH的中点，所以MN是△A′BH的中位线.

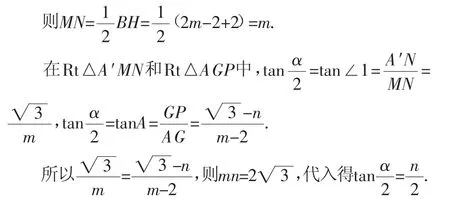
分析：解法4和解法5中，学生从定义出发，求出点的坐标，再由点的坐标发现对称，进而构造出三角形的中位线，利用中位线求出OM或MN的长，使问题得证.

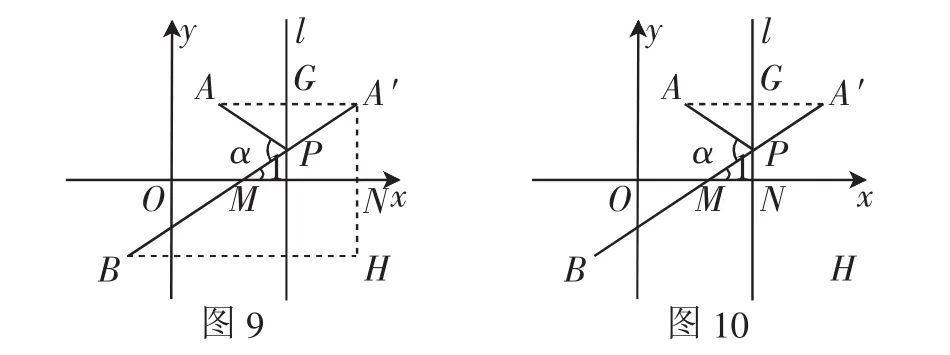
解法6：如图10，因为点P（m，n）是点A、B关于直线l（直线x=m）的等角点，由定义可知A、A′关于直线x=m对称，可求得点A（′2m-2，

分析：解法6和解法7思路简洁，但两种解法中都应用到直线的斜率k的计算公式解法7中还用到了直线的夹角公式和正切倍角公式.学生需要对公式有清晰的认识和理解，并会运用公式，解法7运用了归纳推理和演绎推理相结合的探究方法，这可能得益于创新班学生之笔.

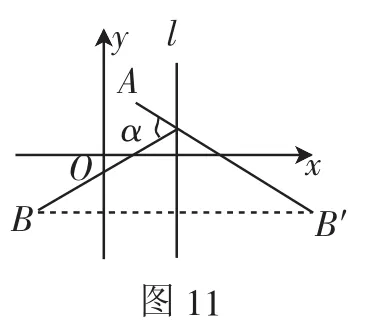
在众多考生中也有不少考生考虑作点B的对称点，构造“等角点”（如图11），其他解法同上文.

四、试题评析

本题以课本例题“最短路径模型”构造新定义.学生感觉模型熟悉，定义简单，其实就是旧知的一个创新.这与近几年南通中考最后一题相比有了很大的变化，本题不再是以抛物线或双曲线为载体，而是根据学生熟知的模型，重新定义，考查学生自主学习、知识迁移与探究的能力.

第（1）问是第（2）问的具体情境.第（1）问的解法为第（2）问提供了解题的思路和方法，意在引导学生由浅入深向第（2）问和第（3）问过渡，安排合理，为学生探究铺路.第（2）问难度不大，但方法灵活，主要是帮助学生克服畏难的心理障碍，为第（3）问探究和创新树立信心.第（3）问紧扣定义，确定P点的轨迹，从而确定直线的位置.

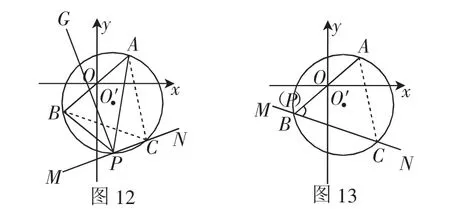
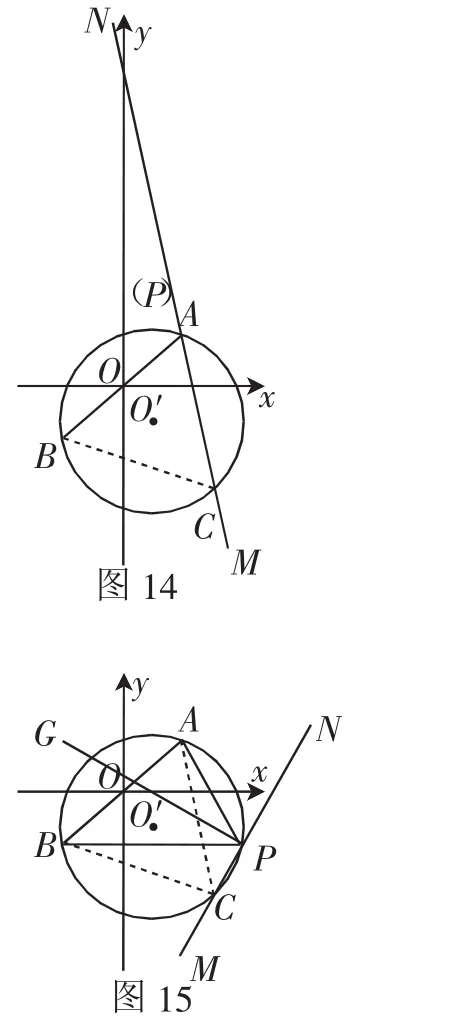
如图12，因为AB长为定值，且∠APB=60°也是定值，所以点P始终在以AB为边的等边三角形的外接圆上.故可在直线AB的右侧以AB为边作等边△ABC，再作△ABC的外接圆⊙O′.根据“等角点”的定义，P是点A、B关于直线y=ax+b（a≠0）的等角点.故直线y=kx+b与直线PA、PB所成锐角相等，即∠BPM=∠APN.又∠APB=60°，所以∠BPM=∠CPN=60°.故可作∠APB的角平分线PG，过P点再作PG的垂线MN即为直线y=ax+b.在⊙O′中，∠APN=∠ABC=60°，所以MN必过点C，即直线y=ax+b必过点C.考虑点P在直线AB的右下方，且点P在⊙O′上，我们可以把直线MN绕着点C旋转寻找点P的可能位置，可以发现经过点B和点A时（如图13和图14），即为第（3）问问题探究的极端情况.当直线y=ax+b平行于x轴时（如图15），a=0，与题意不符，故排除.

当点P、A重合时，直线y=ax+b（a≠0）过点A、C，求得（如图14）.

第（3）问要求学生结合图形探究点和直线的运动变化，观察、分析、归纳、推理，发现结论.优秀学生能展示自己的数学智慧和创新能力，使该题起到了选拔的作用.

五、教学启示

从考生卷面及得分看，对于第（1）问，多数考生可得全分，第（2）问和第（3）问问题较多，一些学生不能把定义的内涵应用于新的情境，如本题中“等角点”的定义，学生未能把等角的条件转化利用，构建相似，一些学生不能利用基本模型，如过B点作直线x=m的垂线，构造“X型”等数学模型构造相似，建立边长关系，不会求解含字母系数的直线的解析式，不会计算与坐标轴的交点的坐标及用含字母m或n的代数式表示线段的长.因此，对数学教学有以下启示.

1.关注基础，理解定义的内涵，实现知识迁移

本题第（1）问和第（2）问难度不大，但许多考生不能把新定义的知识迁移.我们在平时教学中，必须加强定义的理解，掌握定义的内涵，夯实基础.对于新定义的教学，我们首先要深刻理解概念，然后提炼问题结构，再从数形结合的角度揭示问题结构.像上文中找出P点在以AB为边的等边三角形的外接圆上，借助圆研究.课堂教学中，积极引导学生独立思考、反思质疑，加强互动.关注“知识与技能”的发生和发展过程，在应用中不断巩固和深化“双基”，从而让学生真正理解定义的内涵，实现知识的迁移.

2.立足教材，重视基本模型，提升解题能力

教材与教材中的一些数学模型，是中考命题的蓝本，同时是天然的好素材.每年都有大量的新颖试题直接源于教材，或以教材中提供的一些数学模型为基础，经过改造整编、移植借鉴.因此，在平时的教学中，立足教材，重视基本模型，要理解基本图形的关键特征，找准基本图形的核心要素.试题中有的基本图形处于潜伏状态，有时需要通过补充尝试激活基本模型.如上文中作垂直构造“类似K型或X型或A型”模型.我们要让教材成为学生巩固知识、观察、分析、思考、探究问题、发展能力、掌握思想方法的重要渠道，真正实现从“教教材”到“用教材教”的飞跃，以提升解题能力.

3.注重发散，加强思维拓展，培养创新能力

创新思维是时代发展的需要，没有创造性思维的培养就造就不了创新型人才.在平时教学中，鼓励学生再次发现，重新组合，让学生在知识的自主建构中，张开思维和想象的翅膀，寻找问题解决的策略，应尽可能地发散学生的思维.发展学生的求异思维，使其学会从多角度、全方位考虑问题，培养其创新能力.在新定义考题解题教学中，遇到一些直接写结果的设问时，要充分展开思维过程，通过数形结合、动画展示的方式，让学生对解题思路的理解有更直观的认识.

在试卷评阅中发现，有部分考生解题不规范，格式不简明，抓不住得分点.如有学生用P（m，n）、B（-2，-）求直线的解析式，解析式中含两个参数字母，为后续解题设置了障碍.还有考生把表示成，导致错误.还有代数式的变形、化简、计算错误较多.所以平时教学中，一定要严格要求学生，规范解题格式和书写格式，养成正确的解题习惯，提高学业水平，提升数学素养.