正确获取数据信息 培养学生的数学素养
——关于统计与概率中考题给出数据信息的基本方式
☉山东省沂南县第四中学 李树臣
☉山东省荣成第二实验中学 王 华
《义务教育数学课程标准(2011年版)》(以下简称《课标(2011年版)》)指出“数学素养是现代社会每一个公民应该具备的基本素养”,十大“核心概念”是数学素养的重要组成因素.统计与概率方面的内容主要承载着形成与发展学生的数据分析观念、运算能力、推理能力、应用意识等“核心概念”的任务,这对于培养和提高学生的数学素养具有重要的作用.
解答统计与概率方面的问题,首先就是通过阅读题目,获取尽可能多的信息,然后利用这些信息进行解答.学生获取数据信息的能力是学习统计与概率方面的知识、解答与之相关问题的重要基础.
在各地的中考试卷中,有关统计与概率的考题都占有一定的比例,各种题型都有,给出信息的方式众多.仔细阅读、分析2018年各地关于统计与概率部分的中考题发现,考题中给出信息的方式主要有以下八种类型,我们结合具体题目加以分析(所选题目均为2018年各地中考数学试题):
一、用文字语言给出
案例1:(湖南娄底)从2018年高中一年级学生开始,湖南省全面启动高考综合改革,学生学习完必修课程后,可以根据高校相关专业的选课要求和自身兴趣、志向、优势,从思想政治、历史、地理、物理、化学、生物6个科目中,自主选择3个科目参加等级考试.学生A已选物理,还从思想政治、历史、地理3个文科科目中选1科,再从化学、生物2个理科科目中选1科.若他选思想政治、历史、地理的可能性相等,选化学、生物的可能性相等,则选修地理和生物的概率为______.
解:画树状图,如图1所示:
由图1可知,学生A从政治、历史、地理中先选1科,再从化学、生物中选1科,共有6种等可能的结果,其中选修地理和生物的只有1种结果,所以选修地理和生物的概率为
点评:本题以学生选课为背景,与学生的学习现实密切相关,主要考查学生用列表或画树状图的方法求概率的能力,解答的关键是阅读题目,理解题意,正确找出先“从政治、历史、地理中选1科”,再“从化学、生物中选1科”的所有可能情况,并找出选修地理和生物学科的情况数.用列表法或画树状图法求概率适合于两步完成的事件.解答的关键是,首先通过列表或画树状图不重复、不遗漏地列出所有可能的结果,找到总数量及欲求情况的数量,然后根据概率=所求情况数与总情况数之比求出答案.
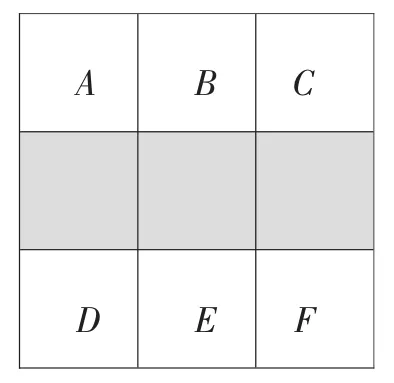
图2
二、用平面图形给出
案例2:(甘肃白银)如图2,在正方形方格中,阴影部分是涂黑3个小正方形所形成的图案.
(1)如果将一粒米随机地抛在这个正方形方格上,那么米粒落在阴影部分的概率是多少?
(2)现从方格内空白的小正方形(A、B、C、D、E、F)中任取2个涂黑,得到新图案,请用列表或画树状图的方法求新图案是轴对称图形的概率.
解:(1)观察图2,发现正方形网格被分成9等份,其中阴影部分面积占其中的3份,所以米粒落在阴影部分的概率是
(2)把从A、B、C、D、E、F中任取2个涂黑的情况列表(如表1):
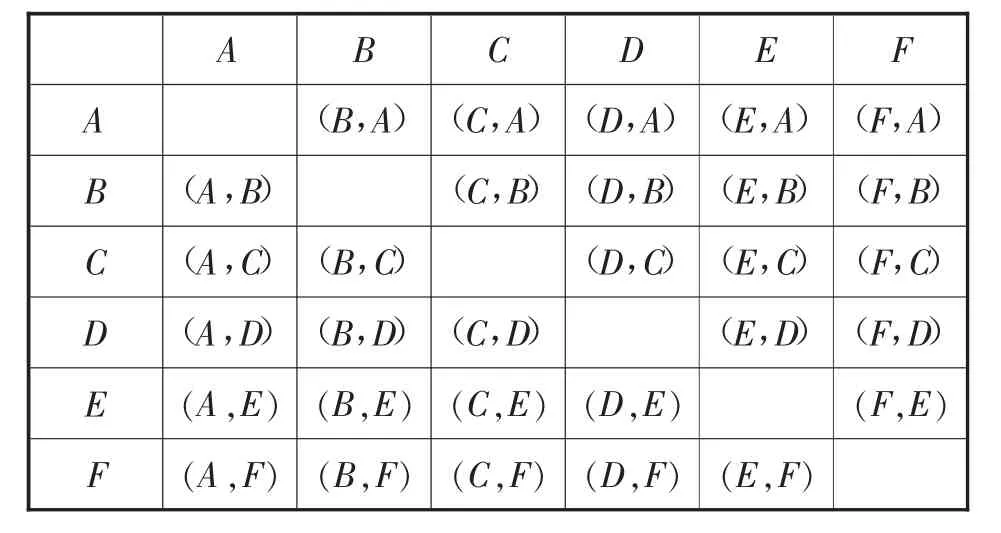
表1
由表1可知,共有30种等可能结果,其中是轴对称图形的有10种,故新图案是轴对称图形的概率为
点评:本题是计算概率的问题,问题中的关键信息“隐含”在平面图形中.解答(1)的关键是观察图形,找出总份数和阴影部分的份数;解答(2)的关键是列出“从A、B、C、D、E、F中任取2个涂黑”的所有情况,再结合图形判断出是轴对称图形的情况数.
三、用表格给出
案例3:(台湾)一个箱子内有4颗相同的球,将4颗球分别标示号码1、2、3、4,今翔翔以每次从箱子内取1颗球且取后放回的方式抽取,并预计取球10次,现已取了8次,取出的结果如表2所示:
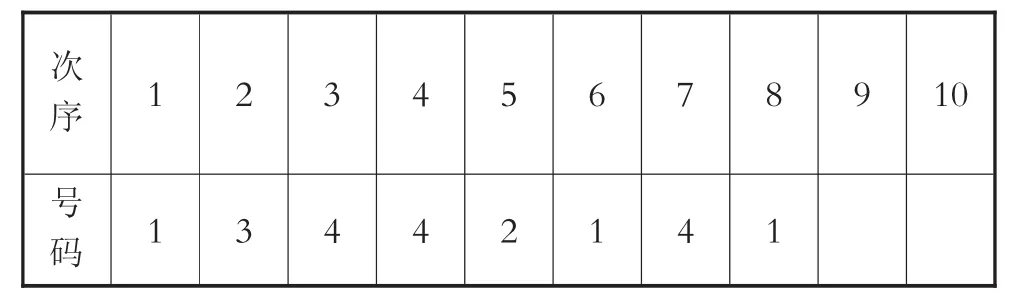
表2
若每次取球时,任一颗球被取到的机会皆相等,且取出的号码即为得分,请回答下列问题:
(1)请求出第1次至第8次得分的平均数.
(2)承(1),翔翔打算依计划继续从箱子里取球2次,请判断是否可能发生“这10次得分的平均数不小于2.2,且不大于2.4”的情形.若有可能,请计算出发生此情形的机率,并完整写出你的解题过程;若不可能,请完整说明你的理由.
(2)因为这10次得分的平均数不小于2.2,且不大于2.4,所以这10次得分之和不小于22,且不大于24,而前8次的得分之和为20,所以后两次的得分之和应不小于2,且不大于4.后两次摸球得分的情况如表3所示:
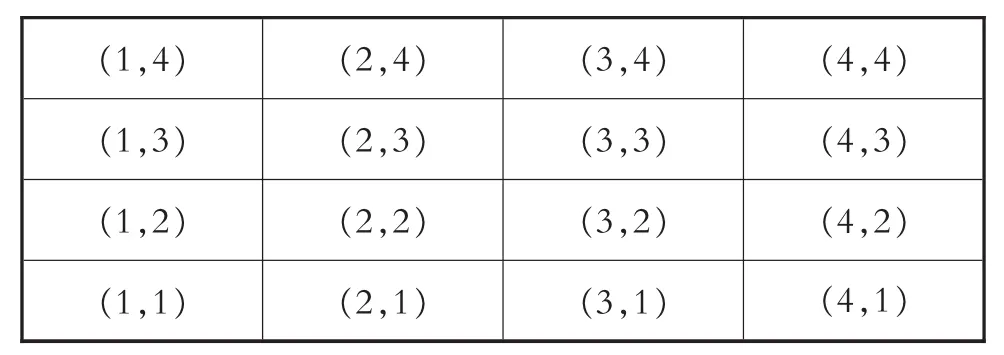
表3
可见一共有16种情况,其中得分之和“不小于2,且不大于4”的有6种结果,所以后两次的得分“不小于2,且不大于4”的机率为
点评:本题第(1)问根据算术平均数的定义列式计算可得;第(2)问需要先根据这10次得分的平均数不小于2.2,且不大于2.4,得出后两次得分的范围,然后用列表法表示出所有等可能的结果,并从中找出“不小于2,且不大于4”的结果数,最后利用概率公式计算可得答案.
解答时根据“这10次得分的平均数不小于2.2,且不大于2.4”推出“这10次得分之和不小于22,且不大于24”,结合前8次的得分之和为20,得到“后两次的得分之和应不小于2,且不大于4”是解题的关键,同时要正确理解“不小于、不大于”的含义.
四、用折线统计图和表格给出
案例4:(山东菏泽)为了发展学生的核心素养,培养学生的综合能力,某中学利用“阳光大课间”,组织学生积极参加丰富多彩的课外活动,学校成立了舞蹈队、足球队、篮球队、毽子队、射击队等,其中射击队在某次训练中,甲、乙两名队员各射击10发子弹,成绩用如图3所示的折线统计图表示:(甲为实线,乙为虚线)
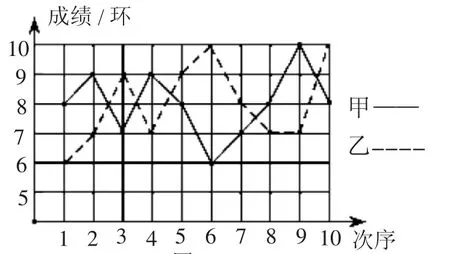
图3
(1)依据折线统计图,得到表4:
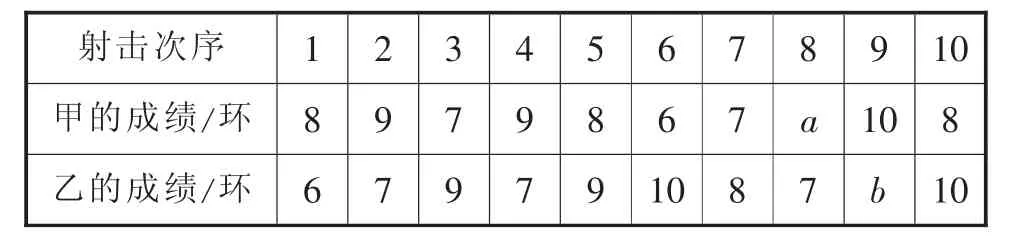
表4
其中a=______,b=______;
(2)甲成绩的众数是______环,乙成绩的中位数是______环;
(3)请运用方差的知识,判断甲、乙两人谁的成绩更稳定;
(4)该校射击队要参加市组织的射击比赛,已预选出2名男同学和2名女同学,现要从这4名同学中任意选取2名同学参加比赛,请用列表或画树状图法,求出恰好选到1男1女的概率.
解:(1)观察折线统计图,可知a=8,b=7.
(2)甲射击10次的成绩中次数最多的是8环,所以甲成绩的众数是8环;乙射击10次的成绩重新排列为:6、7、7、7、7、8、9、9、10、10,则乙成绩的中位数为所以甲成绩的方差为6-8)2+2×(7-8)2+4×(8-8)2+2×(9-8)2+(10-8)2]=1.2(环),乙成绩的平均数为(环),所以乙成绩的方差为[(6-8)2+4×(7-8)2+(8-8)2+2×(9-8)2+2×(10-8)2]=1.8(环),可见,甲的成绩更稳定.
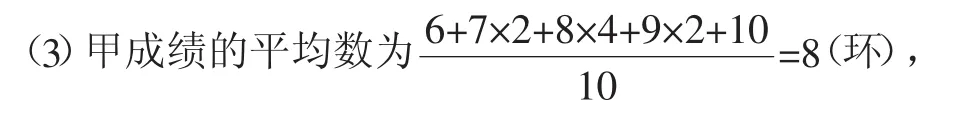
(4)用A、B表示男生,用a、b表示女生,从4名学生中选派2名的情况如表5所示:

表5
显然共有12种等可能的结果,其中一男一女的有8种,所以所求概率
点评:本题以甲、乙两名队员进行射击训练为背景,把两名队员各射击10发子弹的成绩用折线图和表格的形式给出.第(1)题要求学生直接写出表格中a、b的值,这两个值隐含在折线图中,观察可得.第(2)题求甲10次射击成绩的众数,只要找出10个成绩中出现最多的一个数即可;求乙10次射击成绩的中位数,需要把这10个成绩按照从小到大的顺序排列起来,求中间两个数的平均数.第(3)题判断甲、乙两人谁的成绩更稳定,正确计算出甲、乙两人10次成绩的方差是关键.第(4)题用列表法表示出从2名男同学和2名女同学中选出2名同学的所有情况,并找出1男1女的情况是计算概率的关键.
五、用图表和条形图给出
案例5:(湖北潜江)在2018“新技术支持未来教育”的教师培训活动中,会议就“面向未来的学校教育、家庭教育及实践应用演示”等问题进行了互动交流,记者随机采访了部分参会教师,对他们发言的次数进行了统计,并绘制了不完整的统计表(如表6)和条形统计图(如图4).
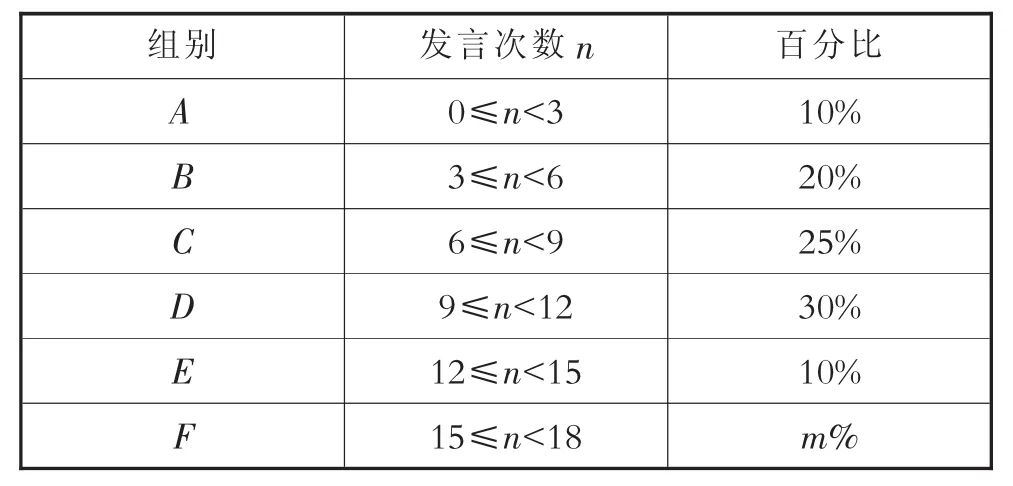
表6
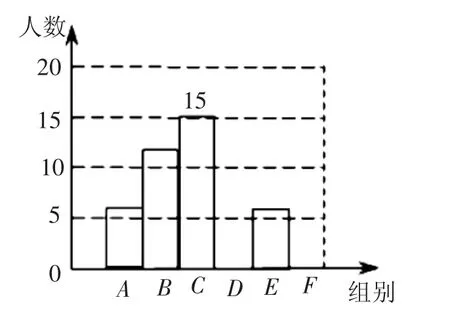
图4
请你根据所给的相关信息,解答下列问题:
(1))本次共随机采访了______名教师,m=______;
(2)补全条形统计图;
(3)已知受访的教师中,E组只有2名女教师,F组恰有1名男教师,现要从E组、F组中分别选派1名教师写总结报告,请用列表法或画树状图的方法,求所选派的2名教师恰好是1男1女的概率.
解:(1)由图4知C组共有15名,从表格中可知C组人数占25%,所以本次共随机采访了15÷25%=60(名),m=100-10-20-25-30-10=5.
(2)D组教师有:60×30%=18(名),F组教师有:60×5%=3(名),补全后的统计图如图5所示:
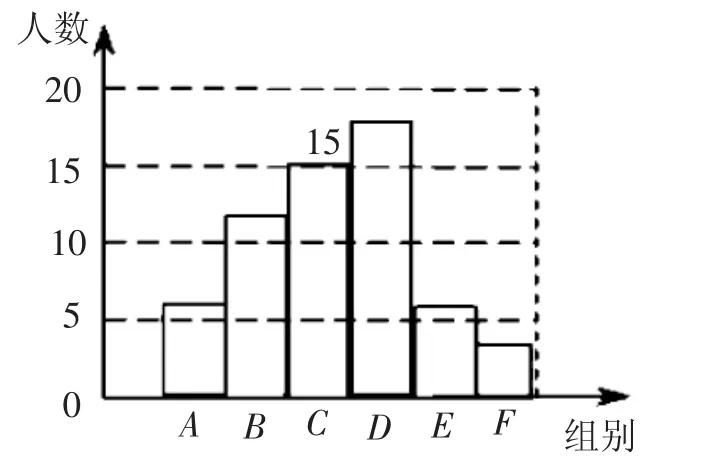
图5
(3)E组共6名教师,4男2女,F组有3名教师,1男2女,从E组、F组中分别选派1名教师的情况用树状图表示,如图6所示:
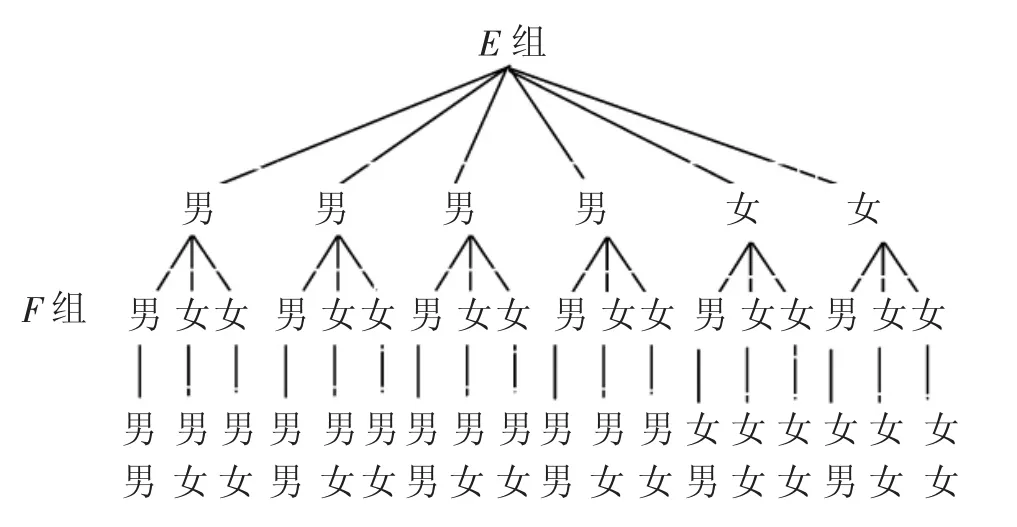
图6
显然共有18种可能,而1男1女的有10种情况,所以所求概率
点评:本题以“教师发言”次数为背景,把发言次数用不完整的表格和条形统计图给出,需要求的一些数据隐含在表格和条形统计图中,学生只要认真阅读题目,从表格和条形统计图中获取有关的信息就能顺利解答.解答第(1)题的关键是从图4中得到C组共有15名教师,从表格中发现C组人数占25%;第(2)题补全条形统计图的前提是先求出D组和F组的教师数;解答第(3)题首先要求出E组和F组的教师数,然后正确画出树状图.
六、用扇形和条形统计图给出
案例6:(天津)某养鸡场有2500只鸡准备对外出售.从中随机抽取了一部分鸡,根据它们的质量(单位:kg),绘制出图7和图8.请根据相关信息,解答下列问题:

图7

图8
(1)图7中m的值为______;
(2)求统计的这组数据的平均数、众数和中位数;
(3)根据样本数据,估计这2500只鸡中质量为2.0kg的约有多少只.
解:(1)m%=1-22%-10%-8%-32%=28%.故m=28.
(2)观察条形统计图.
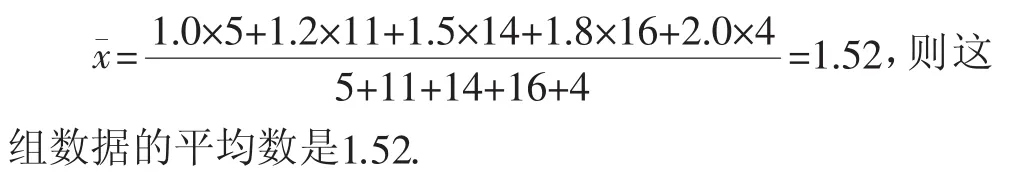
在这组数据中,1.8出现了16次,出现的次数最多,则这组数据的众数为1.8.
将这组数据按从小到大的顺序排列,其中处于中间的两个数都是1.5,则这组数据的中位数为1.5.
(3)因为在所抽取的样本中,质量为2.0kg的数量占8%,所以由样本数据,估计这2500只鸡中质量为2.0kg的数量约占8%,有2500×8%=200(只).所以这2500只鸡中质量为2.0kg的约有200只.
点评:用样本的情况来估计总体是学习统计的目的之一,最近几年各地的中考题中经常提供一个与学习生活或家庭生活有关的问题情境,从中抽取一个样本,把对样本的调查结果用不完整的表格、条形图或扇形统计图给出,让学生们根据它们提供的部分信息求解有关的问题.
本题以“养鸡”为背景,主要考查了平均数、众数、中位数的统计意义及利用样本估计总体等知识.解答本题的前提是认真观察给定的扇形统计图和条形统计图,从中获取有关的信息.解答(1)时利用“五类情况的和等于1”计算;解答(2)时理解“三数”的意义是关键;解答(3)的关键是从图7中找出“质量为2.0kg的数量占8%”.
七、用频数分布直方图和表格给出
案例7:(北京)某年级共有300名学生.为了解该年级学生A、B两门课程的学习情况,从中随机抽取60名学生进行测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
a.A课程成绩的频数分布直方图如图9所示(数据分成6组:40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100);
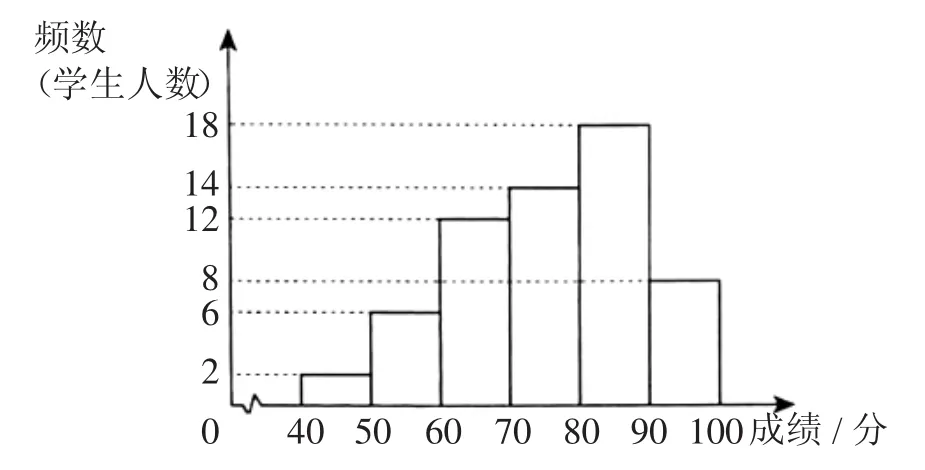
图9
b.A课程成绩在70≤x<80这一组的是:
70 71 71 71 76 76 77 78 78.5 78.5 79 79 79 79.5
c.A、B两门课程成绩的平均数、中位数、众数如表7所示:

表7
根据以上信息,回答下列问题:
(1)写出表中m的值;
(2)在此次测试中,某学生的A课程成绩为76分,B课程成绩为71分,这名学生成绩排名更靠前的课程是________(填“A”或“B”),理由是_______;
(3)假设该年级学生都参加此次测试,估计A课程成绩超过75.8分的人数.
解:(1)共有60个学生参加测试,中位数是第30个数和第31个数的平均数,即=78.75.
(2)该学生A课程成绩为76分,小于A课程样本数据的中位数78.75,说明A课程成绩在后30名,而B课程成绩为72分,大于B课程样本数据的中位数70,说明B课程成绩在前30名.
(3)抽取的60名学生中,A课程成绩超过75.8分的人数为36,所以×300=180(人).
答:该年级学生都参加测试,估计A课程成绩超过75.8分的人数为180.
点评:本题主要考查的知识点有中位数,用样本估计总体.有关的信息隐含在频数分布直方图和表格中.认真阅读频数分布直方图,从中获取数据信息是解答本题的关键.对于第(1)题来说,通过观察直方图,前三组中已有2+6+12=20(个)数据,这60个数据中的第30个和31个都在70≤x<80组中,分别是78.5和79,这是求m的重要前提.第(2)题只要利用A、B两课程样本数据的中位数,判断出该学生A课程成绩在中位数后,而B课程成绩在中位数前即可.解答(3)的关键是通过观察直方图,得到A课程成绩在80≤x<90、90≤x≤100的人数分别是18、8; 借助信息b得到在75.8<x<80范围内的人数为10,从而得到超过75.8分的有36人.
八、用扇形图和频数直方图给出
案例8:(安徽)“校园诗歌大赛”结束后,张老师和李老师将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图(如图10)和频数直方图(如图11).部分信息如下:
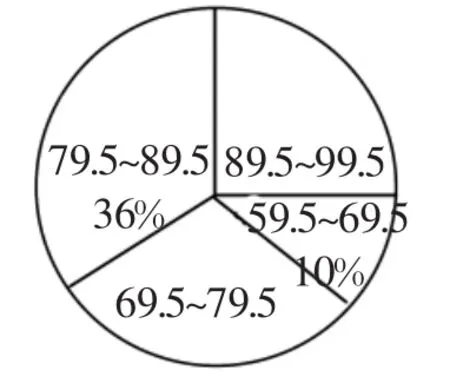
图10
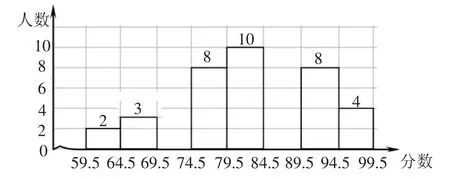
图11
(1)本次比赛参赛选手共有______人,扇形统计图中“69.5~79.5”这一组人数占参赛总人数的百分比为______;
(2)赛前规定,成绩由高到低前60%的参赛选手获奖,某参赛选手的比赛成绩为78分,试判断他能否获奖,并说明理由;
(3)成绩前四名是2名男生和2名女生,若从他们中任选2人作为获奖代表发言,试求恰好选中1男1女的概率.
解:(1)5÷10%=50,所以本次比赛参赛选手共有50人,“89.5~99.5”这一组人数占参赛总人数的百分比为(8+4)÷50×100%=24%,所以“69.5~79.5”这一组人数占参赛总人数的百分比为1-10%-36%-24%=30%.
(2)他不能获奖.理由如下:他的成绩位于“69.5~79.5”这一组,而“59.5~69.5”和“69.5~79.5”两分数段的百分比为10%+30%=40%,因为成绩由高到低前60%的参赛选手获奖,他位于后40%,所以他不能获奖.
(3)画树状图(如图12):
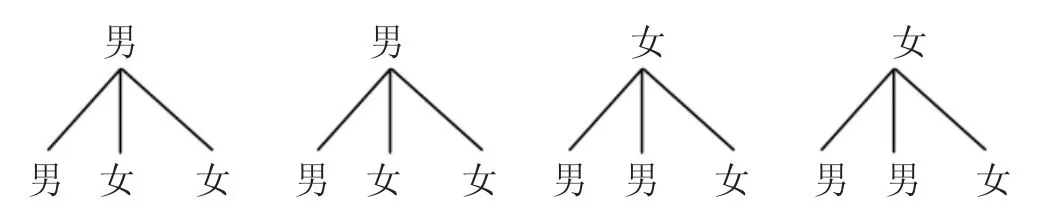
图12
共有12种等可能的结果,其中恰好选中1男1女的结果数为8,所以恰好选中1男1女的概率
点评:本题把“参赛选手的比赛成绩”进行整理,制成扇形统计图和频数直方图,要求从扇形统计图和频数直方图中获取有关的信息,解答与比赛成绩相关的三个问题.求(1)中参赛选手人数的关键是利用扇形统计图中“59.5~69.5”这一组占10%,从直方图中发现这一组有5人.求“69.5~79.5”这一组人数占参赛总人数的百分比时首先应根据扇形统计图和频数直方图求出“89.5~99.5”这一组人数占参赛总人数的百分比,然后利用四个组的和为1进行计算.解答第(2)题的关键是判断成绩为78分的选手位于后40%.求解第(3)题的关键是正确画出树状图.
从前面所举例题中,我们可以发现,统计与概率方面的题目几乎都有生活背景,涉及我们生活的方方面面,这体现出“数学来源于生活”的真理.事实上,统计与概率方面内容主要承载着《课标(2011年版)》提出的数据分析观念、运算能力、推理能力、应用意识等“核心概念”的形成与发展.本部分内容的教学中,我们要结合具体的知识点,加强利用本部分知识解决生活、学习中的实际问题的活动,以培养和发展学生 的应用意识,这样的活动应体现《课标(2011年版)》提出的“问题情境—建立模型—求解验证”的过程,经历这样的过程,可不断培养和提高学生的综合数学素养.

