精英遗传K-medoids聚类算法

宋飞豹，贾瑞玉

安徽大学 计算机科学与技术学院，合肥 230601

1 引言

聚类分析一直是数据挖掘、机器学习、模式识别等领域的重要研究内容之一[1]。K-medoids算法作为应用广泛的聚类算法，近年来，关于K-medoids算法的研究越来越多。文献[2]根据最大最小法则选出k个稠密区域，由此得到k个初始中心点，从而提升了K-medoids的聚类质量；文献[3]通过差分隐私保护技术使K-medoids能够处理增量数据的动态聚类问题；文献[4]通过引入距离加速理论提高了K-medoids聚类的效率。虽然K-medoids聚类算法对离群点的处理效果较好，但K-medoids算法依然存在着初始中心点敏感和聚类结果不稳定等问题。为了解决这些问题，常见的方法是将遗传算法与聚类算法相结合。文献[5]按照最大属性值范围划分法选择聚类中心初值，同时运用两阶段动态选择和变异方法，从而提升了算法的聚类效果。文献[6]提出了在MapReduce架构下的遗传K-medoids算法，该算法使用遗传算法解决K-medoids算法聚类不稳定的问题，使用MapReduce框架解决大数据聚类的问题。虽然遗传算法能够在一定程度上解决K-medoids算法求解结果不稳定的问题，但遗传算法本身也存在着早熟、后期收敛速度慢等问题[7]。文献[8-14]为遗传算法引入了精英策略，提出了基于精英策略改进遗传算法的方法。

虽然精英策略在一定程度上提高了遗传算法的全局收敛性，但是由于聚类算法的特殊性，使精英策略不能直接运用到聚类分析中。在此基础上本文提出了一种精英遗传K-medoids聚类算法（Elite Genetic K-medoids Clustering Algorithm，EG K CA）。该算法使用K-medoids聚类的评价标准作为遗传算法的适应度函数。通过精英个体来保证算法的全局收敛性。同时每次进化的进化团队均通过种群的平均适应度来引入若干随机个体，以提高种群多样性。通过组合交叉和父子竞争的操作提高进化效率。最终通过测试8个具有一定代表性的数据集证明了EGKCA算法的聚类准确率高，求解结果稳定。

2 精英遗传K-medoids聚类算法

2.1 编码方式

传统的二进制编码方式会出现编码长度过长、数据信息读取困难等问题，为了解决这一问题，本文采用一种简单自然的编码方式[6]。设数据样本共有L个数据，中心点个数为k，种群数目为N，则从{ }1,2,…,L 中选择k个值作为进化个体Xi(1≤i≤N)，进化个体Xi中每个等位基因代表每个中心点的位置，基因长度代表中心点的个数。

2.2 精英个体

精英个体best最初是由初始种群s中适应度最高的个体组成的。随着遗传操作的进行，将精英个体best与每次进行遗传操作后产生适应度最高的个体tempmax进行对比，若tempmax的适应度大于best，则更新精英个体，将个体tempmax替换掉原先best的个体。

2.3 适应度函数

其中，ci为划分的中心点(1≤i≤k)；Ci为根据中心点ci划分出来的簇；o是属于簇Ci里面的数据元素；dist为欧式距离。E代表这所有数据元素在中心点集合C={c1,c2,…,ck}下聚类所产生的聚类代价，其值越小，代表簇内距离越小，簇间越紧凑独立，聚类效果越好。

为了体现聚类代价E的作用，本文采用的适应度函数如下：

其中，Xi(1≤i≤N)为种群的一个进化个体，其基因信息代表一个中心点集合；EXi代表数据集A在进化个体Xi下的聚类代价。 f(Xi)的值越大，表示聚类代价越小，聚类的效果越好。 f(Xi)的最大值，即为本文需要求得的最优聚类方案。

2.4 进化团队的产生

传统的遗传算法在求解最优值问题时，面临的最大问题就是早熟现象。遗传算法出现早熟现象的根本原因在于种群在进化过程中由于不断优胜劣汰，使得种群多样性丧失，个体逐渐归于单一。为了解决遗传算法的早熟现象，提高进化效率，本文通过引入rnum个随机个体来替换掉每次遗传操作后形成的进化种群中适应度最差的rnum个个体[8，13]，从而保证了种群的多样性。

为了更好地发挥随机个体的调节作用，本文使得每次产生随机个体的数目与本次进化种群的整体优秀程度有关。种群整体越优秀，所需要的随机个体数目越小，反之，种群整体越差，就需要更多的随机个体为种群产生更多的变化。种群整体评价程度PA可由以下公式求得：

其中，fbest代表种群所经历过的最大适应度；favg为当前种群的平均适应度；fmin代表当前种群的最差适应度。PA越大表示种群整体适应度越小，也就是说种群整体处于一个较差的水平，此时就需要更多的随机个体来为种群增加更多的变化。

随机个体数目的计算公式如下：

其中，τ0、τ1为rnum的调节参数；N为种群个体数目。式（3）、（4）保证了 rnum 的取值范围在 [τ1×N,(τ0+τ1)×N]之间。进化团队的产生模型如图1所示。

图1 进化团队产生模型

2.5 组合交叉

传统遗传算法的交叉方式在处理聚类问题时，由于交叉个体的相似性，容易出现交叉重复、交叉效率低下等问题。为了解决这些问题，文献[13]提出了一种协作交叉操作，通过两个交叉个体差异度来为交叉个体选择合适的交叉方式，从而避免了个体间的无效交叉。但是在聚类分析中进化个体存在着基因数目少，单个基因影响大等问题，使得协作交叉无法直接用在聚类算法中。为此本文通过设计一种适合聚类算法避免无效交叉的交叉算子来对协作交叉进行改进，提出了组合交叉的操作。

定义1（无效交叉点）当参与交叉的两个个体存在相同的中心点时，该中心点和与之对应的交叉点为避免重复均不能参与交叉，此时称该中心点和与之对应的交叉点为无效交叉点。

由定义1可知，无效交叉点的存在严重影响着交叉的质量，为了有效减少无效交叉点的影响，首先需要一个对无效交叉点影响程度的评价标准，本文使用相似度的概念来对两个交叉个体进行评价。

其中，snum表示无效交叉点的个数；k为中心点的个数；u表示两个交叉个体的相似程度，其值越大，无效交叉点所占比重也越大，个体越相似。

定义2（整合交叉）当两个交叉个体存在若干个相同的中心点时，首先将这些相同的中心点从交叉个体中剔除，然后对这两个个体进行普通的单点交叉，最后把单点交叉后得到的两个个体分别加入已剔除的中心点，得到两个新的个体。这就是整合交叉。

为了减轻无效交叉点的影响，本文所提出的组合交叉操作，是根据交叉个体的相似度不断调整交叉方式。当两个交叉个体的相似度u≤u0时，使用普通的单点交叉，此时，单点交叉只需要避免重复即可；当两个交叉个体的相似度u＞u0时，使用整合交叉。

2.6 变异

由于聚类算法的特殊性，使得算法在进行遗传操作过程中必须保持中心点数目不变，也就是k值的不可变性，同时也必须保证每个进化个体不存在相同的中心点。也就是说每个进化个体必须存储含k个不同中心点的信息，这也是为什么在交叉过程中必须要避免重复的原因。

在变异过程中为了避免重复，首先从进化个体Xi中选择一个变异点sm(1≤sm≤k)，然后从与Xi相对应的非中心点集合中，随机找到一个非中心点的位置替换掉sm中的内容。这样既实现了变异的需求，又可以保证中心点不重复。

2.7 父子竞争

在传统的遗传算法中，经常出现“子不如父”的现象，即遗传操作后的子代种群整体适应度不如父代种群的现象。出现这一现象的一个主要原因是交叉变异的不可控性。个体进行交叉变异时，交叉变异的结果具有一定的随机性，个体的适应度有可能变得更好，也有可能变得更差。为了尽量控制个体的交叉变异向着一个比较正确的方向进行，本文提出了一种父子竞争的操作。

定义3（父子竞争）将交叉变异后得到的子代个体与父代个体进行对比，若父代个体的适应度大于子代个体，则保留父代个体作为新种群的成员，同时该父代个体不再参与交叉变异；反之，则保留子代个体，该父代个体依然可以参与交叉变异。

2.8 EG K CA算法描述

输入：数据集A，中心点个数k。

输出：聚类中心点集合。

步骤1初始化种群s、精英个体best。

步骤2根据K-medoids算法计算每个个体的适应度，并根据式（4）生成rnum个随机个体，替换掉适应度最差的rnum个个体，形成进化团队t。

步骤3更新精英个体best，将精英个体best替换掉进化团队t中适应度最差的个体，然后将精英个体best与进化团队t中适应度最高的个体temp进行对比，若temp的适应度大于best，则用temp替换掉精英个体best。

步骤4遗传操作形成新种群：

（1）使用轮盘赌选择法选择两个进化个体；

（2）组合交叉，求两个进化个体的相似度u，若u≤u0时，使用单点交叉，若u＞u0时，使用整合交叉；

（3）变异，首先从进化个体中选出一个变异点，然后从非中心点集合中选取一个替换掉变异点的内容；

（4）父子竞争。

步骤5判断是否满足终止条件，若是，则结束，否则转步骤2。

3 仿真实验

为了验证EG K CA聚类的有效性，实验将其与K-medoids算法和标准遗传K-medoids聚类算法（Standard Genetic K-medoids Clustering Algorithm，SG K CA）进行对比。其中SG K CA算法除了编码方式与EG K CA相同，交叉变异需要避免重复之外，其他操作与标准遗传算法相同。本文分别选择4个人工数据集和4个从UCI挑选的真实数据集进行实验。

3.1 真实的数据集

本文从UCI中分别选取了两个数据型数据集和两个分类属性数据集[1]。两个数据型数据集分别为Iris和Wine；两个分类属性数据集为Zoo和Soybean。4个数据集的大体内容如表1所示。

表1 真实数据集的描述

本文为EG K CA和SG K CA设置的迭代次数为200代，将3个算法分别运行20次得到的聚类代价结果如表2所示。由表2可知，相对于K-medoids和SG K CA，EG K CA对4个数据集求得聚类总代价的最大值、最小值和平均值均最小。对比K-medoids和SG K CA，除了Wine数据集中SG K CA求得的平均值优于K-medoids外，其他均不如K-medoids。这也是一般遗传算法容易陷入早熟现象的又一体现。而K-medoids算法本身为各个数据集求得的聚类代价的最大值和最小值也有一定的差距，这说明了K-medoids也具有一定的不稳定性。

表2 3个算法在4个真实数据集中求得的聚类代价

对于聚类准确性的判断，本文使用Sun等人[15]提出的准确率判定方法，具体判定方法如下：

其中，ai是出现在第i个类簇（执行算法得到的）及其对应类（初始类）中的样本数；k为聚类簇的个数；L是样品总数。3个算法求解真实数据集的平均准确率见图2。由图2可知，对比K-medoids和SG K CA，在Wine和Zoo中两者的平均准确率有少许差别，而在Iris和Soybean中两者的平均准确率一致。在这4个数据集中，EG K CA求得的平均准确率均高于K-medoids和SG K CA。从而说明了EG K CA聚类更加准确。

图2 真实数据集求解的平均准确率分布图

3个算法对4个真实数据集求解10次得到的最优聚类代价如图3～图6所示。对于这4个真实数据集，EG K CA求得的聚类代价最优、最为稳定。K-medoids和SG K CA求得的聚类代价均大于EG K CA，且均有一定的不稳定性。

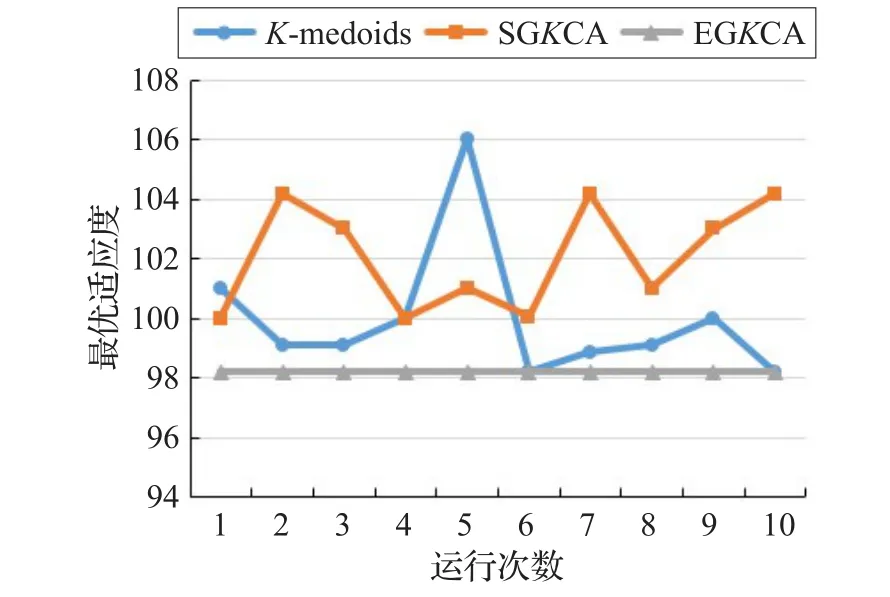
图3 Iris中求解10次的聚类代价分布图

图4 Wine中求解10次的聚类代价分布图

图5 Soybean中求解10次的聚类代价分布图

图6 Zoo中求解10次的聚类代价分布图

3.2 人工数据集

为了验证聚类算法在不同数据分布下的聚类效果，本文设计了4个人工数据集[5]：人工数据集1（AD1）是测试类簇间距离较大时的聚类；人工数据集2（AD2）是测试类簇间距离较小且存在边界重合时的聚类；人工数据集3（AD3）是测试大类中包含小类时的聚类；人工数据集4（AD4）是测试存在多个类时的聚类。4个数据集的分布情况如图7，大致状况如表3所示。

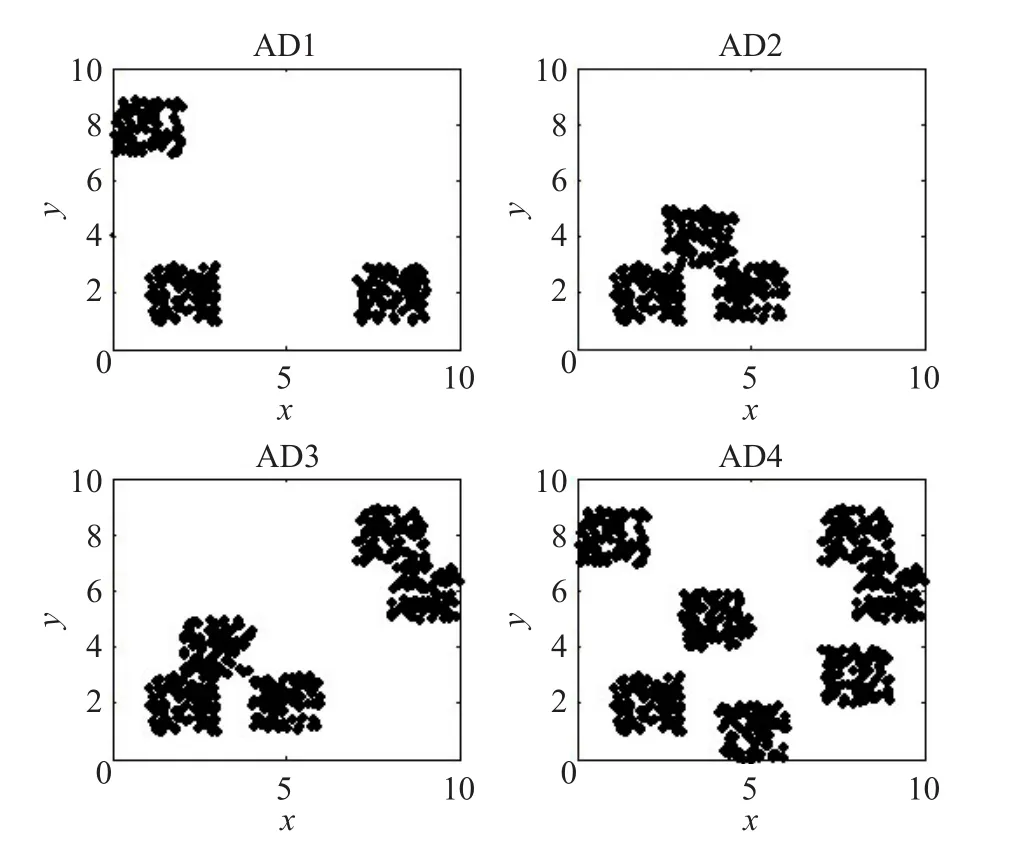
图7 人工数据集的分布图

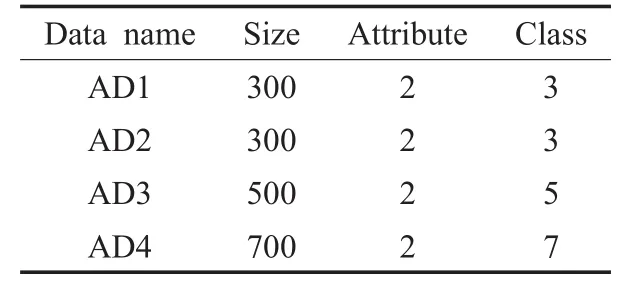
表3 人工数据集的描述

表4 各算法对人工数据集聚类情况

3个算法对4个人工数据集求解10次得到的最优聚类代价如图8～图11所示。对于这4个人工数据集，EG K CA求得的聚类代价最优、最为稳定。K-medoids和SG K CA求得的聚类代价均大于EG K CA，且均有一定的不稳定性。

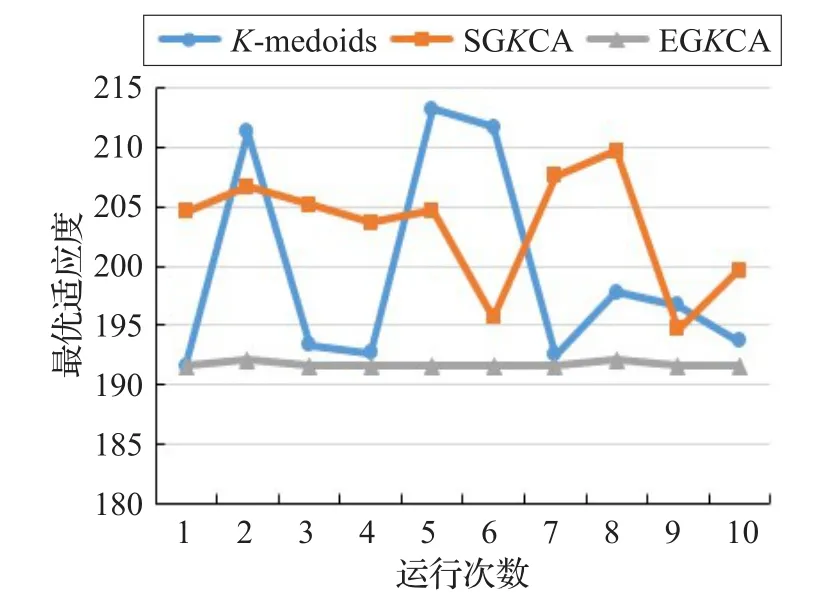
图8 AD1中求解10次的聚类代价分布图

图9 AD2中求解10次的聚类代价分布图

图10 AD3中求解10次的聚类代价分布图

图11 AD4中求解10次的聚类代价分布图

4 总结

本文针对传统K-medoids算法寻优能力差，求解结果不稳定等问题，提出了精英遗传K-medoids聚类算法。该算法通过精英策略增加种群全局收敛性；通过引入以种群适应度为基础生成的若干随机个体减少了早熟现象的影响；通过组合交叉的方式提高了进化效率；通过父子竞争一定程度上控制了遗传算法自身随机性带来的消极影响。8个不同的数据集的测试结果证明了该算法对不同分布情况的数据集均有较好的聚类效果，结果也比较稳定。

目前不存在普遍适用的聚类算法，因此，未来的研究方向还应放在如何处理含有多个离群点或分布规律不明显的数据集的聚类上。