基于邻域引力学习的生物地理学优化算法

马 萍，刘思含，孙根云，张爱竹 ，郝艳玲

1.中国石油大学（华东）地球科学与技术学院，山东 青岛 266580

2.青岛海洋国家实验室 海洋矿产资源评价与探测技术功能实验室，山东 青岛 266071

3.环境保护部卫星环境应用中心 国家环境保护卫星遥感重点实验室，北京 100094

1 引言

生物地理学优化算法（Biogeography-Based Optimization，BBO）是Simon[1]于2008年提出的一种新型的元启发式算法。该算法受生物地理学启发，通过模拟生物物种在栖息地之间的迁移、变异和灭绝实现栖息地之间信息的交流和共享，达到搜寻问题最优解的目的[2]。

BBO算法具有操作简单、参数少、收敛快速等优点[3]，但是该算法在搜索过程中容易发生早熟收敛而陷入局部最优[4]。造成这一现象的直接原因是在迁移操作中，栖息地的更新仅仅通过简单的解变量替换的方式进行，导致算法开采新解的能力较差[4]；同时，“轮盘赌”策略选择的迁出栖息地大部分为优秀解，使得种群主要向优秀栖息地学习，进一步加快了种群多样性的丧失，致使算法陷入停滞状态[5]。为解决这一问题，研究者们提出了多种改进策略。毕晓君等[5]改进了BBO算法的迁移操作，采用动态方法选取迁出栖息地，并运用一种混合迁移策略指导物种迁移，增强了算法对解的搜索能力；Boussaid等[6]将DE算法与BBO算法相结合，提出了双阶段差分生物地理学优化算法，利用DE算法的搜索能力提高了算法的种群多样性；龚文引等[7]采用了三种变异机制代替BBO算法的随机变异策略，并利用实数编码的形式将算法拓展到了连续域，有效地提高了BBO算法的全局搜索能力；徐志丹等[8]在BBO算法迁移策略的基础上提出了扰动迁移算子，增强了群体的多样性，提高了算法解决MOP的能力。这些改进策略均在一定程度上提高了BBO算法的优化性能，但大部分算法忽略了栖息地之间物种迁移的自然规律，没有充分考虑栖息地之间的距离和适应度对物种迁移的影响。

为解决上述问题，本文提出了一种基于邻域引力学习的生物地理学优化算法（Neighbor Force Learning Biogeography-Based Optimization，NFBBO）。新算法采用基于邻域的选择策略，使迁入栖息地向其邻域中最邻近且优秀的栖息地学习，充分利用栖息地的邻域信息，增加种群多样性。同时采用引力学习的方式对迁入栖息地进行更新，使其解变量的变化受迁出栖息地适应度和距离的共同影响，拓展解空间，提高算法的搜索能力。为了使算法更好地跳出局部最优，提出了一种自适应的高斯变异机制，通过10个具有不同特点的测试函数[9-10]进行对比实验，结果表明了本文算法的有效性和优越性。

2 背景知识

2.1 生物地理学优化算法

在自然界中，物种生存在不同的栖息地中，适合物种生存的栖息地具有高的适应度指数（Habitat Suitability Index，HSI）。影响适应度指数的因素，如温度、雨量和植被的多样性等称为适应度指数变量（Suitability Index Variable，SIV）。在BBO算法中，每个栖息地对应一个优化问题的候选解其中N是解的个数，D是解的维度，评价栖息地好坏的适应度指数对应优化问题的适应度函数。算法中优秀的解对应高HSI的栖息地，较差的解对应低HSI的栖息地。根据生物地理学理论，HSI值高的栖息地适合居住，物种数较多且趋于饱和，对栖息地空间和资源的竞争激烈，因此接纳新物种迁入的能力较差，具有较高的迁出率和较低的迁入率。相反，HSI值低的栖息地，物种数量少，因此有很大的空间和资源，具备较高的迁入率和较低的迁出率。栖息地之间物种的迁入和迁出提供了不同栖息地之间信息交流的途径，较差栖息地可以通过接受优秀栖息地的物种迁移提高自身的质量。栖息地Xi的迁入率λi和迁出率μi，可以由以下公式计算得到：

式中，I和E分别为最大迁入率和迁出率；si为栖息地Xi的物种数量；smax为每个栖息地可容纳的最大物种数量。

BBO算法通过迁移操作实现栖息地的更新。对于栖息地Xi的第d维解变量，如果满足迁入条件，则按照下列方式进行迁移操作：（1）通过“轮盘赌”策略选取满足条件的迁出栖息地Xi；（2）用迁出栖息地对应维度的解变量代替原有栖息地的解变量。BBO算法通过这种解变量替换的方式，使较差栖息地共享优秀栖息地的解分量而得到进化。

为了增强种群多样性，使算法跳出局部最优，BBO算法在执行完迁移操作之后，设置了一个变异操作，栖息地的变异概率为：

其中，mmax为初始变异率；Pi为各个栖息地的物种数量概率；Pmax为所有物种数量概率的最大值。

变异操作中，对于栖息地Xi的第d维解变量，若随机产生的[0，1]之间的随机数小于其变异率mi，则采用随机变异策略随机产生一个新的解分量代替原解分量。变异算子可以使栖息地的一个或多个解分量发生变化，增加种群的多样性。BBO算法的详细流程介绍见文献[1]。

2.2 万有引力定律

作为宇宙中四种基本相互作用力之一的万有引力，由Newton于1687年提出[11]。在牛顿万有引力定律中，宇宙空间中任意两个物体之间都相互吸引，且引力的大小与它们质量的乘积成正比，与它们之间距离的平方成反比[11]，即：

其中，G为万有引力常数；M1和M2分别为两个物体的质量；R12为两个物体之间的距离。根据牛顿第二定律，物体1在物体2的万有引力作用下产生的运动加速度为：

从式（4）中可以看出，万有引力定律反应了物体质量和距离对引力影响的规律：在同等距离下，质量大的物体吸引力更大；在质量相等的情况下，距离越近的物体受到的引力越大。万有引力定律的这一特性，和自然界中物种迁移规律有着相同之处，即物种的迁移与栖息地之间距离的远近和适应度值有关。因此，本文将引力定律应用到BBO算法中，构建新的栖息地更新策略，提高算法的搜索能力。

3 生物地理学优化算法

在自然界中，栖息地适应度的提高是通过物种迁移实现的[1]。物种在不同栖息地之间进行迁移时，需要同时考虑两个因素：栖息地适应度和距离。低适应度的栖息地通过接受高适应度栖息地的物种迁移提高自身的质量。物种迁出栖息地的适应度越高，其物种间的竞争也就越激烈，导致迁出的物种对环境的适应能力更强，对迁入栖息地的影响更大。同时，根据地理学邻近效应原理[12]，栖息地更容易受到邻近栖息地的影响。这主要是因为物种会选择距离较近的栖息地进行迁移，迁移距离越远，物种被猎杀的风险也就越高，距离越近，物种保留得越好[13]。因此，在两个迁出栖息地适应度相同的情况下，迁移距离近的影响大。特别地，当栖息地距离较远时，即使是高适应度的迁出栖息地，对迁入栖息地的影响也较小。栖息地之间的这种相互关系与引力规律非常类似，因而可以利用引力定律来描述不同物种迁移对栖息地的影响。

原始BBO算法的迁移操作忽略了上述栖息地之间复杂的迁移关系，通过“轮盘赌”的策略选择迁出栖息地，并对满足迁入条件的栖息地通过解变量替换的形式进行更新[1]。“轮盘赌”策略虽可有效地选取较优的栖息地作为迁出栖息地，但是该选择方式具有一定的随机性，忽视了栖息地之间距离和适应度对物种迁移的影响。解向量替换的更新方式使得迁入栖息地完全被动地接收迁出栖息地的信息，导致搜索空间不再产生新的变量，仅仅是当前所有解变量的组合，栖息地之间迅速趋于相似，种群多样性降低[4-5]。为了增加算法的种群多样性，跳出局部最优，BBO算法采用随机变异策略对栖息地进行变异操作。但是这种变异方式忽略了种群的状态信息，对新解的搜索能力较差，特别是在迭代后期，当种群候选解和最优解较为接近时，随机变异不仅很难勘探出较优解，还容易产生很多较差解，造成计算资源的浪费[5]。

基于以上分析，本文提出一种基于邻域引力学习的迁移算子。在该算子中，对满足迁入条件的栖息地采用“适应度距离比”的方法从其邻域中选择迁出栖息地。同时，采用引力学习的方式对迁入栖息地进行更新，不同物种迁移的影响与距离和适应度有关。在此基础上，为了弥补BBO算法随机变异策略的不足，引入一种自适应的高斯变异策略，利用当前种群的信息进行随机扰动，并根据进化过程调整变异强度，使算法能够自适应地跳出局部最优，寻找更优解。

3.1 NFBBO迁移策略

其中，栖息地Xi的r个邻域是根据适应度值排序之后，依顺序在Xi的两边选取r/2个栖息地组成。这样，迁入栖息地就可以向其邻域中最邻近且优秀的栖息地学习。在选择出合适的迁出栖息地之后，采用引力学习的策略对迁入栖息地进行更新：

其中，rand为[0，1]之间的随机数；M(Xk)为栖息地Xk的质量，计算公式为：

式（7）中A是空间尺度因子，随着当前解空间的扩大或缩小而增减，计算公式为：

其中，Xd(u)和Xd(l)分别是当前种群的第d维解变量的最大值和最小值。

NFBBO迁移算子的具体步骤如算法1所示。

算法1 NFBBO迁移算子

1.按照适应度值对栖息地进行排序，并划分邻域

2.计算所有粒子的迁入率λ和迁出率μ

4. For d=1 to D do

5. If rand(0,1)＜λi

6. 按照式（6）从Xi的r个邻域选择迁出栖息地Xdk

7. 按照式（7）更新Xdi

8. End If

9. End for

10.End for

中外运-敦豪国际航空快件有限公司近日在其北京总部举行媒体发布会，宣布其珠海口岸正式落成并投入使用，成为落户珠海口岸国际快递监管中心的首家国际快递公司。此外，DHL正式宣布将持续加大在中国的战略投资，对外公开了今年以来的一系列投资举措。DHL称，借助港珠澳大桥带来的高效物流通道，DHL珠海口岸的建立将大幅提升珠江西岸地区国际物流的快递效率。随着2018年10月24日港珠澳大桥正式通车，由珠海口岸清关的国际快递转运至其香港转运中心（DHL全球三大转运中心之一）的时间将从原来的4小时缩短为45分钟，大大提升了转运时效。而这对于专业做国际限时快递服务的DHL来说，尤为重要。

与BBO算法迁移算子不同，NFBBO算法中采用了邻域选择策略确定迁出栖息地，充分利用了每个栖息地邻域粒子的距离和适应度信息，有效避免了“轮盘赌”策略大概率选择高适应度栖息地所造成的早熟收敛问题，增加了算法的种群多样性，并且适应度信息的运用保证了算法搜索精度。同时，引力学习的更新策略直接源于基本的万有引力定律，使得迁入栖息地的改变受物种迁移距离和适应度的综合影响，产生了新的解变量，拓展了解空间；空间尺度因子的引入，可以根据种群的收敛状态调节引力的大小，提高了算法的搜索能力。

3.2 自适应的高斯变异机制

为了使算法跳出局部最优，BBO算法采用了随机变异策略。但是该变异策略忽略了种群在不同进化过程中的状态差异，搜索新解的能力较差[5]。为了使算法更好地搜索到全局最优解，在迭代初期，应使种群更大程度地遍布整个搜索空间，较快地定位最优解的范围；在迭代后期使种群聚集在最优值的邻域范围内，进行更精细的搜索[8]。

基于这一点，本文提出一种自适应的高斯变异机制。与随机变异不同，高斯变异是在原解的周围产生一个服从高斯分布的随机扰动[14]，公式为：

式中，Gaussian(0 ,σ)是服从均值为0方差为σ的高斯分布随机变量。受文献[15]启发，文中方差σ随着迭代次数逐渐递减：

其中，itermax是算法的最大迭代次数；t是算法的当前迭代次数。在迭代初期，σ值较大，高斯变异可以产生较大的扰动步长，增大算法的搜索范围；而在迭代后期，σ变小，产生的扰动步长较小，主要在当前候选解的局部范围进行精细搜索。同时，变异步长的计算利用了栖息地信息，因此，高斯变异机制可以根据不同栖息地在不同进化过程中的状态自适应地产生变异粒子，更加高效地搜索新解，跳出局部最优。

自适应的高斯变异的步骤如算法2所示。

算法2自适应的高斯变异

1.计算所有粒子的变异率m

2.For i=1 to N do

3. For d=1 to D do

4. If mi＞rand

6. End if

7. End for

8.End for

3.3 NFBBO算法流程

基于邻域引力学习的生物地理学优化算法的流程如图1所示。

图1 NFBBO算法流程图

4 实验结果与分析

4.1 测试函数

为验证算法的有效性，本文采用10个具有不同特点的测试函数进行函数优化实验。测试函数的维度D均为30，其表达式、搜索空间S以及真值o如表1所示。其中F1～F2为经典测试函数中的单峰函数[9]，只有一个最优值，可以检验算法的收敛特性[5]；F3～F5为经典测试函数中的多峰函数[9]，含有多个局部极小值，反映了算法跳出局部最优，逼近全局最优解的能力[5]；F6～F10为CEC2015旋转平移测试函数[10]，其全局最优点不再位于搜索空间的中心，且函数变量之间彼此不相关，用来检验算法解决复杂优化问题的能力。

4.2 参数设置

本文采用基本的BBO[1]算法以及目前改进效果较好的 PBBO[16]算法、DBBO[6]算法和 RCBBO[7]算法作为对比算法。为了保证对比实验的公平性，所有算法的终止条件均设置为最大适应度计算数，FEsmax=50 000，种群大小为N=50。同时为了发挥各个对比算法最优的性能，算法的其他参数都按照原文献经过测试后的参数进行设定。NFBBO算法中最大迁入率E=1，最大迁出率I=1,初始变异率mmax=0.1,邻域大小

表1 测试函数

对每个优化函数，每个算法独立运行30次，取运行结果的平均值Mean、标准差Std、运行时间runtime[10]进行比较。此外，本文采用Wilcoxon秩和检验法[17]对不同算法进行非参统计检验，置信度α=0.05。非参检验的实验结果由“h”表示，其中“+”表示测试结果本文算法显著占优，；“-”表示测试结果其他算法显著占优；“=”表示测试结果不显著，即本文算法与其他算法所得的结果无显著性差异。

4.3 实验结果及分析

实验结果如表2所示，可以看出，NFBBO算法在所有函数上获得的Mean值都是最小的，要明显优于其他4种对比算法，充分表现了本文算法在搜索能力和搜索精度上的优越性。这主要是因为NFBBO算法迁移操作中的邻域选择策略充分利用了栖息地的邻域信息，增加了种群的多样性；引力学习的更新方式拓展了解空间，提高了搜索能力，其中空间因子的使用还可以调节搜索的步长，更好地找到全局最优解的范围，并在后期进行精细的搜索。对于含有多个局部极小值的多峰函数F3和F5，NFBBO算法的优化效果更为显著，是唯一一个搜索到真值的算法，而其他算法在这两个函数上的优化效果都较差。这表明NFBBO使得种群能够有效地跳出局部最优，收敛到全局最优。在处理复杂的CEC2015测试函数时，5种算法所得到的平均最优值结果都不太理想，这主要是因为旋转平移函数本身比较复杂，函数变量之间不相关，且真值不在函数的搜索空间中心处，加大了全局最优解的搜索难度。同时，BBO算法本身不具备旋转不变特性，因此基于BBO改进的策略在CEC2015函数上效果较差。即便如此，相比较于其他4种对比算法，NFBBO算法的处理效果仍然是最优的。这些实验结果都证明了本文算法在处理不同特点的函数优化问题时的优越性。同时从表2中各个算法的“Std”值可以看出，NFBBO算法具有较好的稳定性。除了函数F7和F10，NFBBO算法的标准差在其他8个测试函数的结果中都是最小的，且效果突出。

对于算法的搜索效率和收敛速度可以从实验结果表2的runtime和收敛特性曲线中得出。由表2可知，NEBBO算法的运算时间在所有单峰函数和多峰函数上都是最小的，验证了NEBBO高效的运算速度。尤其是在具有一个局部极值的单峰函数F2上，NEBBO的运算速度明显优于其他对比算法。图2给出了5种算法对部分测试函数的收敛特性曲线，图中分别采用了5种不同的线型表示不同的对比算法。从图2中可以看出，NFBBO算法具有优良的收敛性能。对于经典的单峰和多峰函数F1、F2和F5，NFBBO算法在演化的初始阶段收敛速度就明显快于其他4种对比算法，表现出其优越的搜索能力，能迅速找到优秀解所在的区域。同时，在收敛曲线中，NFBBO算法搜索到的最优值也是最小的，具有较高的收敛精度。但是对一些复杂的CEC2015测试函数，算法的收敛速度有所变慢。对函数F6，在演化初期，NFBBO算法收敛曲线的下降速度要慢于PBBO和DBBO，但是随着迭代的进行，NFBBO算法的收敛速度明显加快，且达到最好的收敛精度。同样在函数F8的演化过程中，初期阶段NFBBO算法收敛速度要慢于其他算法，随后曲线下降速度加快，当其他4种对比算法的收敛曲线不再变化，陷入局部最优时，NFBBO算法的收敛曲线能够继续下降且收敛到了最好的结果。与以上CEC2015测试函数不同，对F10，NFBBO算法表现出了明显的收敛性能优势，在整个演化过程中，NFBBO算法的收敛速度均是最快的且达到了最好的收敛精度。基于以上分析，可以得出NFBBO算法具有较快的收敛速度，在处理复杂的函数问题时，能够很好地跳出局部最优，拓展新的搜索区域，找到更加优秀的解集。

表2 5种算法在不同测试函数上的性能对比

表2统计了对比算法之间的非参检验结果。从结果中可以看到，除函数F6、F7和F8，其他函数的非参检验结果均为“+”，即与其他对比算法相比，NFBBO算法具有显著的优越性。对函数F6和F7，NFBBO算法要显著优于BBO和RCBBO，与PBBO、DBBO算法无显著性差异。对函数F8，与PBBO算法无显著差异，但是要显著优于其他函数。从整个非参检验的结果可以得出，NFBBO算法与其他优化算法相比具有显著的优越性。

5 结束语

BBO算法具有较快的收敛速度，但其搜索能力较差，容易发生早熟收敛，陷入局部最优。为了克服这一缺点，本文提出一种基于邻域引力学习的迁移算子，该算子采用邻域选择策略确定迁出栖息地，并利用引力学习的方式对栖息地进行更新，增加了种群多样性，提高了算法的搜索能力。同时引入了自适应高斯变异机制，充分利用了当前解的信息，使算法能够自适应地跳出局部最优。从实验结果中可以得出，NFBBO算法不仅收敛速度较其他算法快，而且可以更大程度上逼近全局最优解，在收敛速度和收敛精度上较标准BBO算法有较大提高。

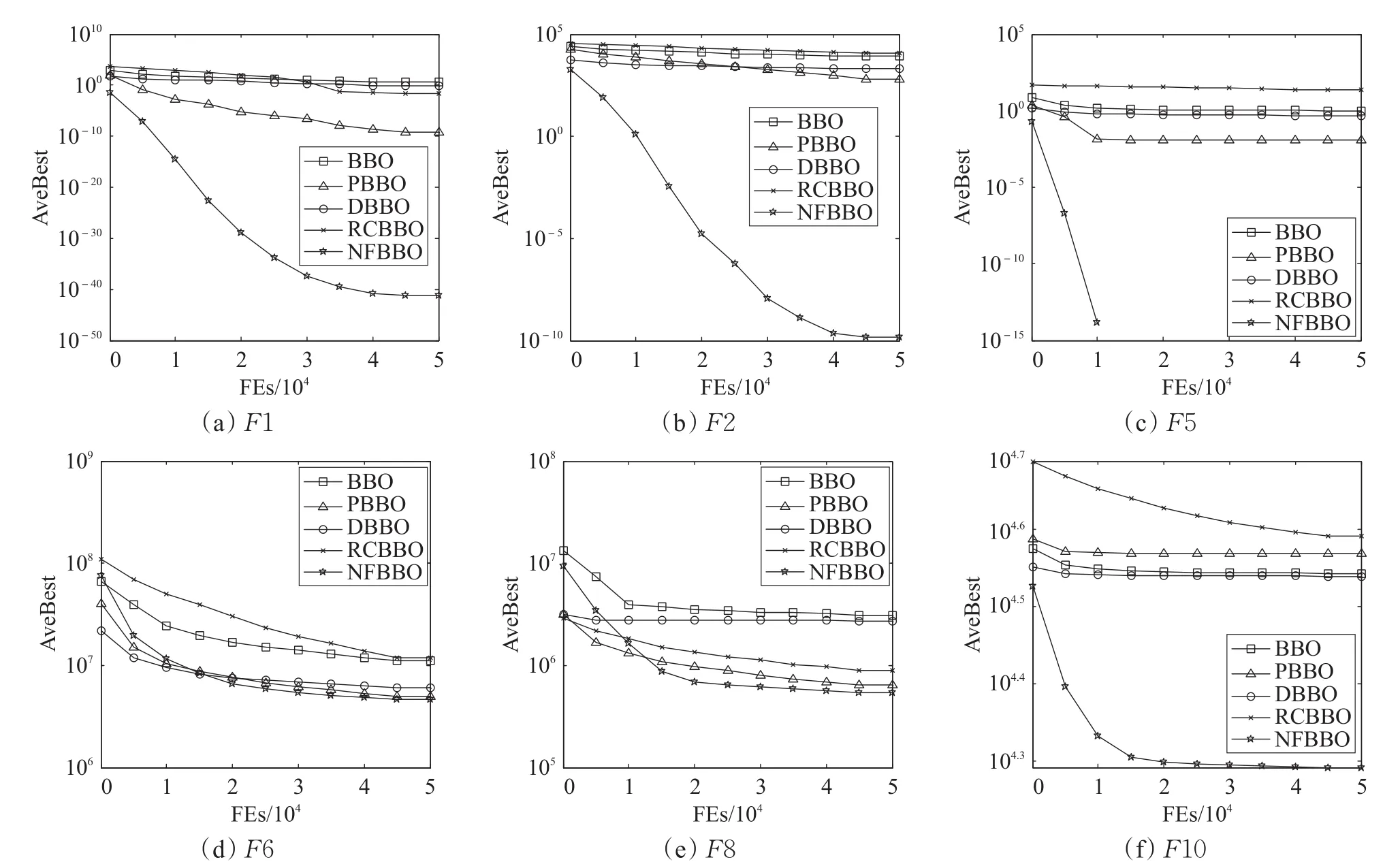
图2 BBO、PBBO、DBBO、RCBBO与NFBBO在部分测试函数上的收敛曲线图