特殊循环结构的过程挖掘算法

贺朝阳，杜玉越，王 路

山东科技大学 计算机科学与工程学院，山东 青岛 266590

1 引言

过程挖掘在数据挖掘和过程建模与分析两个领域的知识之间搭建桥梁，从事件日志中提取知识，进而发现、监控和改进实际过程。有三种类型的过程挖掘场景使用了事件日志，分别为过程发现、一致性检测和过程增强[1]。过程发现是使用不包含先验信息的日志挖掘得到模型；一致性检测是比较日志实际情况和挖掘的过程模型是否吻合，或者比较已知模型与其产生的日志的情况是否吻合；过程增强是对于一个已存在的过程，利用实际过程产生的日志对其进行改进或扩展。

在过程挖掘中，日志完备性至关重要。完备性与噪声类似，噪声表示日志中含有过多数据问题，而完备性表示日志中含有数据过少问题。缺少特殊日志行为的非完备事件日志将会对挖掘算法的实际工作产生影响，导致无法挖掘正确模型。噪声和完备性描述了关于事件日志的质量问题，而模型质量的度量需要从不同维度来描述。过程模型有拟合度、精确度、泛化度和简洁度这四个主要度量维度。模型的拟合度表示事件日志中的迹在过程模型中的重演能力，拟合度高的模型说明其允许事件日志中所反映的行为发生。模型的精确度决定模型是否允许日志以外的行为出现，模型精确度高说明其不允许过多日志以外的行为发生。模型的泛化度代表模型不仅仅局限于日志中的行为，允许更多额外行为。简洁度好的模型说明是能够解释日志中所见行为并且最简单的模型。

目前，国内外学者提出了许多过程挖掘算法。文献[2]提出了挖掘工作流模型的α算法，并证明了能准确挖掘出的模型种类。从实践日志中挖掘过程模型时，很多实际业务流程对应的工作流模型中存在复杂结构，如非自由选择结构（non-free-choices）、不可见任务（invisible tasks）、重名任务（duplicate tasks）以及长短不一的循环结构（loop）。α算法通过分析日志中活动之间的依赖关系来挖掘模型。这些依赖关系的定义基于局部日志行为，对于短循环和非自由选择结构等复杂结构无法处理。文献[3]提出的α+算法扩展了α算法，针对长度为1和2的短循环进行挖掘。文献[4]在此基础上提出了能够处理非自由选择结构的α++算法。文献[5]利用启发式规则发现日志中的循环任务和重复任务，提出了τ算法。文献[6]基于启发式挖掘算法，扩展了长距离依赖关系的度量，对多个模型进行并行挖掘，提升了针对短循环以及长距离依赖的挖掘效果。文献[7]和[8]将遗传算法应用于过程挖掘，解决了非自由选择结构、不可见任务以及重名任务等复杂结构的挖掘问题。文献[9]提出了一种层次化拟合功能，结合了遗传算法和启发式算法，能够处理包含不可见任务和循环结构等多种复杂结构。基于语言的区域挖掘[10-11]、基于状态的区域挖掘[12]以及ILP挖掘算法[13]对模型的拟合度有很好的保证。在现有的挖掘算法中，大多基于完备事件日志进行过程挖掘，然而实际业务过程中存在非完备日志的情况。文献[14]针对块状结构过程模型的挖掘，提出了IM算法，可以对非完备的日志进行挖掘，并且挖掘得到的模型具有极高的拟合度。文献[15]定义了因果完备日志，基于这种非完备日志，提出了针对块状并发结构进行挖掘的α||算法。

在不考虑重名活动的情况下，对于存在循环结构的事件日志，同一条迹中一定存在出现次数大于2的活动。对于α系列算法，当循环结构与其他结构处于并发关系时，其定义的活动间依赖关系存在局限。对于同一循环结构中的活动在日志的迹中没有连续出现时，α系列算法将不能正确地发现嵌套在并发结构中的循环结构。本文针对存在循环结构的日志完备性进行了探讨，给出了新的定义，并针对一种特殊循环结构的挖掘提出了αfsl算法。该算法主要通过预处理日志以及后处理添加结构实现，主要目标为在重新定义的循环完备日志中挖掘存在于并发结构中的特殊循环结构。

2 基本概念

本章描述了多重集合[16]、序列、迹[17]、事件日志、Petri网[18-19]、工作流网[20]、α算法[2]等基本概念。在本文中，N代表一个自然数集合，N={ }0,1,2,…。

定义1（多重集合）设S是一个集合，一个S上的多重集合定义为一个函数Z:S→N。Β()S代表了S上的所有多重集合组成的集合。

定义2（序列）设S是一个集合，S*是S上所有有限序列组成的集合。是一个序列，σ[i]表示序列σ中第i个元素，|σ|表示序列σ的长度。

σ是一个序列，对于∀a∈σ，σ(a)表示a在σ中出现的次数。例如

定义3（迹）设A是活动集合，一条迹σ∈A*是一个活动的队列。

定义4（事件日志）事件日志L是迹σ的多重集合，记为L∈Β( )A*。

Petri网是由库所（place）和变迁（transition）组成的有向二分图。

定义5（Petri网）三元组 PN=(P ,T;F)称为一个Petri网，其中P是一个有限库所集，T是一个有限变迁集，是一个有限弧集。对于变迁t∈T ，∙t表示t的输入集，t∙表示t的输出集。

在本文中，模型中的变迁和日志中的活动一一对应，在一些情况下不进行区分。工作流网是一个有着唯一初始库所和终止库所的Petri网。

定义6（工作流网）五元组WFN=( )P,T;F,i,o称为一个工作流网当且仅当：

（1）PN=( )P,T;F 为一个Petri网；

（4）对于∀x∈P⋃T，x在一条从i到o的路径上。

定义7（基本活动次序关系）令W是一个覆盖T工作流日志，i.e.,W∈Β( )T*。令a,b∈T：

跟随关系a＞Wb：当且仅当存在一条迹使得 σ∈W,ti=a并且ti+1=b；

因果关系a→Wb：当且仅当a＞Wb并且b≯Wa；

定义8（α算法）[2]令W代表覆盖T的工作流日志。α(W)定义如下：

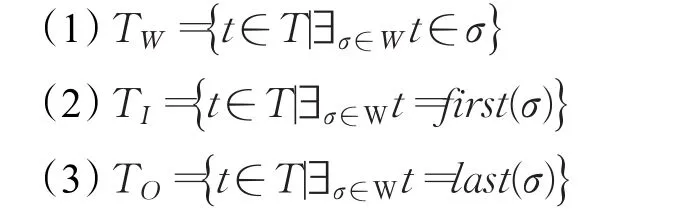
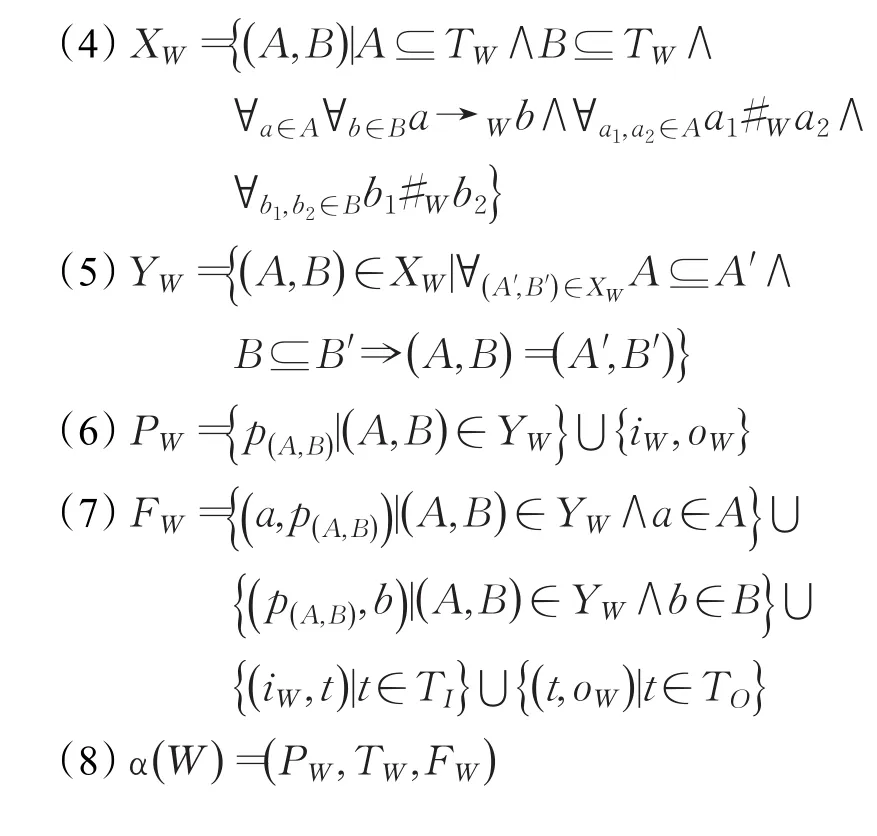
3 自由单循环结构

本章说明了α算法及其衍生算法挖掘特殊循环结构时的局限，并给出了自由单循环结构及自由单循环完备日志的定义。

在挖掘并发结构中嵌套的循环结构时，α算法及其衍生算法都存在一定的局限性。

首先，针对不同长度循环结构进行挖掘时，α算法存在以下局限：对于长度为1的循环结构（即自环结构），α算法会将循环结构中的活动识别为与模型其他部分独立的一个活动；对于长度为2的循环结构，结构中的两个活动互相存在跟随关系，与并发关系的定义完全一致，即α算法无法区分长度为2的循环结构和由两个活动组成的并发结构；对于长度为3以及更长的循环结构，α算法能够正确挖掘。因为循环中包含3个及以上活动时，采用跟随关系即(＞W)能够清楚地表达并且区分并发结构和循环结构。

在日志完备的前提下，对于α算法的衍生算法，包括α+算法等，通过后处理等方法添加了长度为1的循环结构；通过预处理重新定义并发关系等方法，解决了长度为2的循环结构和并发结构的区分问题。

当并发结构中存在循环结构时，如果日志中没有包含明确的循环结构的特征（即循环结构中包含的活动连续多次出现），现有的α算法及其部分衍生算法便不能正确地发现存在于并发结构中的循环结构。图1展示了两种并发结构中嵌套循环结构的情况。图（a）中WFN1表示了长度为1的循环结构与单个活动处于并发结构的情况，图（b）中WFN2表示了三种不同长度的循环结构处于并发结构的情况。

本文仅针对如图1（a）、（b）中的这类循环结构嵌套在并发结构的情况进行挖掘，但循环结构的长度和数量不局限于图中情况。

图1 两种并发结构嵌套循环结构情况

当日志中任何一条迹中不包含连续多次出现的活动或者活动集，例如等情况，使用α算法及其部分衍生算法不能有效挖掘并发结构中嵌套的此类循环结构。

对于图1（a）、（b）中的这类循环结构，其起始库所和终止库所为同一个库所，本文中称为自由单循环结构。此类循环结构自由的特点表现为日志中至少存在一条迹不包含该循环结构中的活动，而且该循环结构是一个单循环，即循环内部是顺序结构，没有其他的分支结构。图2展示了不同长度的自由单循环结构的例子。图（a）中WFN3含有长度为1的自由单循环结构，图（b）中WFN4含有长度为2的自由单循环结构，图（c）中WFN5含有长度为3的自由单循环结构。

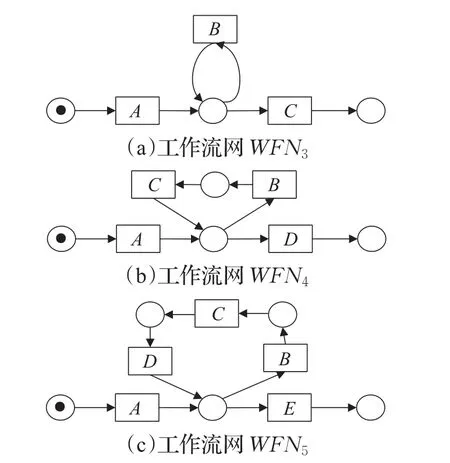
图2 三种长度的自由单循环结构

定义9（自由单循环结构）设WFN=(P ,T;F,i,o)为一个工作流网，FSL是WFN的一个自由单循环结构当且仅当FSL=(P ′,T′;F′,i′,o′)，其中T且表示组成 FSL中变迁的个数，i′=o′。T′中的变迁组成的序列 TS∈T′*，对于 TS ，有其中TS[1]为 FSL的初始变迁为FSL的终止变迁tend。

对于图2（c）中WFN5所表示的长度为3的自由单循环结构，其tstart为B，tend为D，自由单循环序列TS为

在不考虑表示偏好的情况下，日志的一条迹中如果多次出现同样活动，即说明存在循环结构。对于α算法，存在活动a和b，根据跟随关系＞W定义，如果有a＞Wb以及b＞Wa，便不能判断活动a与活动b是存在于长度为2的循环结构的两个活动，还是存在于并发结构中的两个活动。在α算法的衍生算法α+算法中，通过重新定义并发关系和因果关系来对长度为2的循环进行处理。其定义的并发关系中不存在一条迹中有的情况，对于这种情况，当作因果关系a→Wb处理。

对于一个自由单循环结构，tstart表示结构中的第一个变迁，即该结构在日志中的起始活动对应的变迁；tend表示结构中的最后一个变迁，即该结构在日志中的终止活动对应的变迁；TS表示该结构中所有的变迁对应的日志中的活动按顺序组成的序列，即自由单循环序列。该序列的顺序为该循环结构在日志的迹中出现第一遍时各活动的顺序。

对于并发结构中嵌套循环结构的情况，如果日志是非完备的，即日志的任何一条迹中的重复活动没有连续出现，而是穿插了与其并发的其他活动，例如σ=这类情况，α算法及其衍生算法不能正确挖掘。这些算法将嵌套在并发结构中的循环结构识别为普通顺序结构或者错误结构，不能表现存在重复活动的情况。对于包含循环结构的模型对应的日志，存在某一条迹中有活动出现次数不小于两次，即循环结构中的活动在一条迹中出现至少两次，但不需要一定连续出现。因此，对于包含自由单循环结构的日志定义如下。

定义10（自由单循环完备日志）设WFN=(P,T;F,i,o)为一个工作流网，，日志Wfsl为WFN的自由单循环完备日志当且仅当：（1）对于∀ti,tj∈T ，有且不存在，其中＞Wfsl表示自由单循环完备日志中的跟随关系，＞N表示模型中的跟随关系；（2）对于自由单循环完备日志Wfsl中的任意一条迹σ，当时，不存在一条长度为k(k＞0)的子序列，使得

自由单循环完备日志是一种针对并发结构中嵌套循环结构情况存在的非完备日志，日志中的跟随关系在模型中都存在，但日志中任何一条迹中不包含连续多次出现的活动或者活动集，例如或 σ=等情况。

对于图1（a）中的WFN1，其自由单循环完备日志可以是Wfsl1={ACD,ABCD,ACBD,ABCBD}。对于该日志中的每一条迹，都不存在连续重复的活动，但存在重复活动B。

4 自由单循环结构挖掘算法

对于如何发现自由单循环结构，本文主要提出三个阶段的工作。

（1）寻找日志中存在的重复活动。

（2）通过日志中重复活动与前后活动之间的关系区分不同自由单循环结构中的活动。

（3）挖掘每个自由单循环结构，得到其自由单循环序列TS，根据TS得到结构内部活动之间的关系。

4.1 寻找重复活动

在不考虑表示偏好的前提下，针对并发结构中嵌套的自由单循环结构挖掘，根据自由单循环完备日志的定义，在日志的一条迹中所有出现次数大于1的活动，都属于自由单循环结构中的活动。对于这些活动，给出重复活动的定义。

定义11（重复活动）设A为活动集合，为自由单循环完备日志，若∃a∈A，σ∈Wfsl，有a∈σ，且，称a是一个重复活动。

对于所有的重复活动，这些活动是在日志的某一条迹中重复出现，即自由单循环结构中的活动，但并没有划分到具体的自由单循环结构中。例如图1（b）中的WFN2，对于它的一个自由单循环完备日志：

根据定义得到的重复活动为{ }B,C,D,E,F,G ，包含了所有在日志的某一条迹中重复出现的活动。

4.2 发现重复活动的前驱活动和后继活动

定义12（迹前驱活动和迹后继活动）设A为活动集合，Wfsl∈Β(A*)为一个自由单循环完备日志。对于任意重复活动a，存在迹，使得a∈σ，有 ai=a(1 ＜i＜n )，称ai-1为a的迹前驱活动，ai+1为a的迹后继活动。

对于任意重复活动，日志的每一条迹中所有该活动的迹前驱活动组成其迹活动前集TracePreSet，所有该活动的迹后继活动组成其迹活动后集TracePostSet。例如图1（b）中的WFN2及其日志Wfsl2，可以得到活动

通过给出迹前驱活动和迹后继活动的定义，对已发现的重复活动存在于具体的自由单循环结构进行区分。

B的TracePreSet为{A,C,D,E,F,G},TracePostSet为{C,D,E,F,G,H}。活动C的TracePreSet为{A,B,D,E,F,G}，TracePostSet为{B,D,E,F,G}。活动D的TracePreSet为 {B,C,E,F,G}，TracePostSet为 {B,C,E,F,G,H}。活动E的TracePreSet为{A,B,C,D,G},TracePostSet为{B,C,D,F}。活动F的TracePreSet为{B,C,D,E}，TracePostSet为{B,C,D,G}。活动G的TracePreSet为 {B,C,D,F}，TracePostSet为 {B,C,D,E,H}。

4.3 获取自由单循环序列

对于不同长度的自由单循环结构中的活动，其迹活动前集和迹活动后集存在一定关联。关联的具体情形主要有两种：一种是长度为2的自由单循环结构中内部的活动自身的迹活动前集和迹活动后集之间存在关联；另一种是多个长度不为2的自由单循环结构之间的活动的迹活动前集和迹活动后集存在关联。首先是发现并区分出长度为2的自由单循环中的活动，由以下定理判断。

定理1设WFN=( )P,T;F,i,o为一个工作流网，Wfsl为WFN的自由单循环完备日志，FSL标识WFN的自由单循环结构。对任意重复活动a：

证明假设 a为 FSL中的活动，对于 ∀b∈a.TracePreSet,有b＞Wa或；对于∀c∈TracePostSet,有a＞Wc或a→Wc。

且对于∀c∈TracePostSet有a→Wc,所以a为FSL.tstart且

（2）与（1）的证明类似。

由定理1可知，当一个活动的迹活动后集是前集的真子集，说明该活动是一个长度为2的自由单循环结构中的tstart对应的日志中的起始活动，将此类活动加入到长度为2的自由单循环结构的tstart组成的集合L2TstartSet；当该活动的迹活动前集是后集的真子集，说明该活动是一个长度为2的自由单循环结构中的tend对应的日志中的终止活动，将此类活动加入到长度为2的自由单循环结构的tend组成的集合L2Tend Set；当一个活动的迹活动前后集合不互为真子集，说明该活动存在于长度不为2的自由单循环结构中，将这些活动加入长度不为2的重复活动集合NoL2ASet。

对于L2TstartSet中每一个起始活动，遍历日志中的每一条迹，在集合L2Tend Set中必定存在一个终止活动在每一条迹中都与该起始活动出现次数相同。该起始活动与该终止活动存在于同一个长度为2的自由单循环结构，因此得到该结构有序的自由单循环序列TS。对于区分其他长度不为2的自由单循环结构中的活动，即NoL2ASet中的活动，通过以下定理判断。

定理2设WFN=( )P,T;F,i,o为一个工作流网，A为活动集合，Wfsl∈Β( )A*为WFN的自由单循环完备日志，NoL2ASet是Wfsl的长度不为2的重复活动集合，FSL标识WFN的自由单循环结构。对∀a,b∈NoL2ASet,且,若,则a、b属于同一个FSL。

证明用反证法。假设活动a、b不属于同一个FSL,即，可知 ∃p∈A ，有因为，所以

根据定理2，对于集合NoL2ASet中的活动，如果存在两个活动处于同一自由单循环结构中，这两个活动的迹活动前集交集与后集交集应该相同，即包含其他所有与该自由单循环结构并发的活动。对于每个长度为1的自由单循环结构，其自由短循环序列TS为单个活动；对于每个长度大于2的自由单循环结构，通过遍历日志，当存在一条迹出现该结构中的活动时，按照活动第一遍出现的顺序排序，得到该结构的自由单循环序列TS。

根据上述两种情况，下面给出获取所有自由单循环序列的算法。

算法1自由单循环序列获取算法

输入：自由单循环完备日志Wfsl、重复活动集合RASet、每个重复活动的迹活动的前集TracePreSet和后集TracePostSet。

输出：自由单循环序列集合FSLSet。

照迹中出现的顺序排序

算法1所有重复活动根据不同情况划分到各自的自由单循环结构中，得到其自由单循环序列TS。第2行到第8行根据定理1区分不同长度的自由单循环结构中的活动，并加入相应的集合中。第9行到第15行，对于长度为2的自由单循环结构中的tstart和tend进行匹配。遍历日志中的每一条迹，对每一个起始活动tstart，找到与之对应的终止活动tend，得到自由单循环序列TS。第16行到第22行根据定理2对长度不为2的自由单循环结构中的活动进行匹配，得到无序集合S。对于每一个S中的活动，日志中存在一条迹含有这些活动。按照这条迹中这些活动首次出现的顺序将S中的活动按序添加到有序的自由单循环序列TS中。所有的自由单循环序列TS组成自由单循环序列集合FSLSet。

对于图1（b）中的WFN2及其日志Wfsl2，首先挖掘其中长度为2自由单循环结构。对于活动C，根据算法2，C.TracePostSet⊆C.TracePreSet，因此C 为某一个长度为2的循环结构中tstart对应的起始活动，加入 集合 L2TstartSet。对于活动 D,D.TracePreSet⊆D.TracePostSet,因此D属于某一个长度为2的循环结构的tend对应的终止活动，加入集合L2Tend Set。遍历日志中的每一条，发现活动C和活动D在每条迹中出现的次数相同，可知活动C与活动D属于同一个长度为2的自由单循环结构，将加入所有自由单循环序列集合FSLSet。对于其他的重复活动B、E、F、G，加入长度不为2的重复活动集合NoL2ASet。根据算法1，通过判断每两个活动的迹活动前集交集和后集交集，可以发现活动B与其他活动的前集交集和后集交集都不相同，可知活动B属于一个长度为1的自由单循环结构，将加入所有自由单循环序列集合FSLSet。其他三个活动E、F、G两两之间的迹活动前集交集和后集交集都是{B ,C,D} ，可知活动E、F、G属于同一个自由单循环结构，得到包含活动E、F、G的无序集合S。根据日志中的任意一条包含活动E、F以及G的迹，例如，可以得到包含这些活动的自由单循环结构的，并将其加入自由单循环序列集合FSLSet。至此，日志Wfsl2中所有自由单循环结构已经全部发现，自由单循环序列集合FSLSet为

4.4 日志活动的次序关系

定义13（自由单循环关系）令Wfsl是一个自由单循环完备日志，i.e.,Wfsl∈Β(T*)。令a,b∈T：

根据图1（b）中的WFN2及其日志Wfsl2，以及其自由单循环序列集合FSLSet，对于每个自由单循环结构中的活动，前后相继的活动之间的关系变为，即和

根据自由单循环关系，能够正确发现自由单循环结构中各活动之间的关系，而α算法及其衍生算法对自由单循环结构内部活动关系不能正确发现，会错误地识别为并发关系或者跟随关系。

对于自由单循环序列集合FSLSet中每一个自由单循环结构，其中活动之间的基本次序关系重新定义为自由单循环关系。

4.5 αfsl算法

根据日志预处理工作得到的不同自由单循环结构对应的自由单循环序列，发现各个结构内部活动之间的自由单循环关系，为αfsl算法的模型挖掘工作提供支持。

αfsl算法是针对并发结构中嵌套的自由单循环结构进行挖掘，基于α算法实现。在预处理阶段，通过对日志的处理，发现其中存在的重复活动，进而获得所有自由单循环序列。通过对自由单循环结构内部活动之间次序的重新定义，正确发现自由单循环结构中各活动之间的关系，进而挖掘出合理的模型。下面给出αfsl算法的定义。

定义14（αfsl算法）令W代表覆盖T的自由单循环完备工作流日志。αfsl( )W 定义如下：

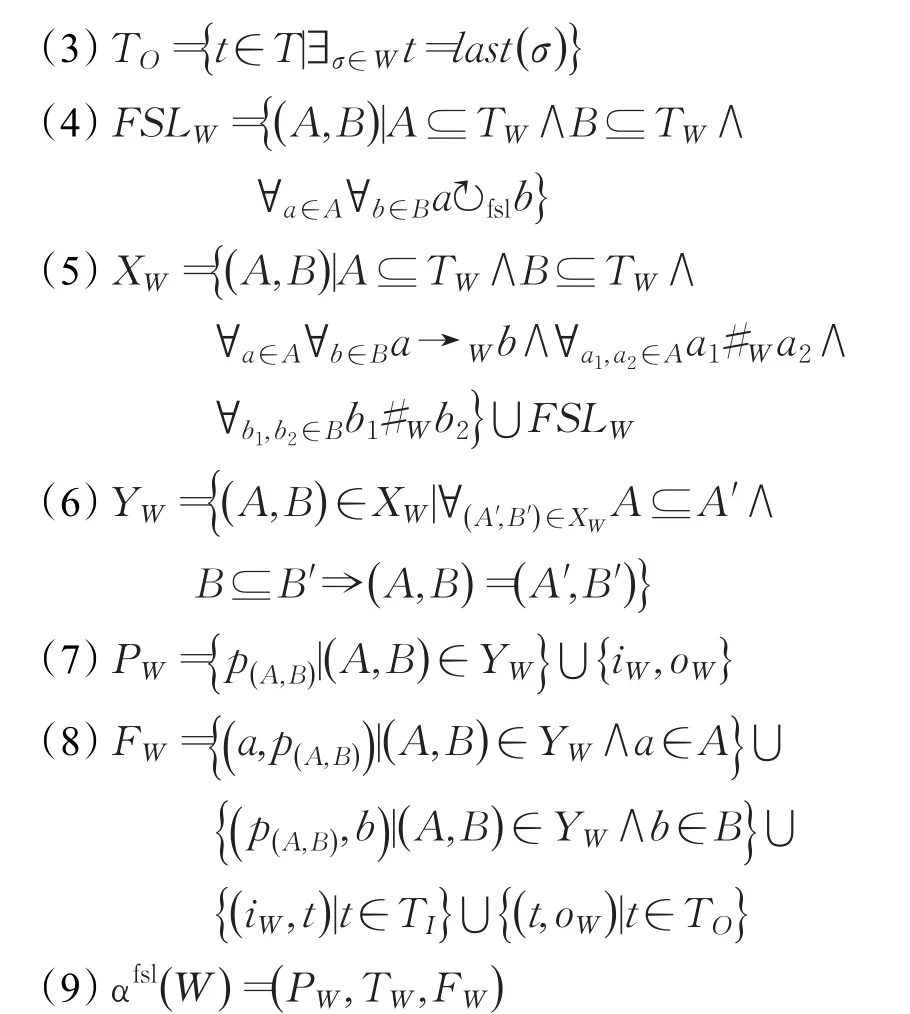
αfsl算法针对并发结构中嵌套的自由单循环结构进行挖掘。在该算法中，扩展了α算法定义的日志中不同活动之间的关系，加入了第四步过程。在第四步中，根据算法1获得所有FSL的TS，发现FSL内部活动之间的自由单循环关系并加入到α算法中。具体实现时，利用α算法挖掘不包含FSL的部分模型，并在α算法挖掘到部分模型的基础上通过后处理的方式插入所有FSL，最终得到正确模型。

5 仿真实验

本文通过实验验证算法的可行性以及分析结果。αfsl算法已经作为插件（https：//pan.baidu.com/s/1pK7zSuR）在开源过程挖掘框架ProM中实现，它以XES格式的日志作为输入，以工作流网表示的过程模型为输出。实验使用Java语言编写插件，硬件环境为Windows7 SP1操作系统、Intel®CoreTM2.50 GHz处理器以及10.0 GB内存。

以某电脑维修公司网上维修的业务流程为例，客户的电脑出现故障，从申请维修业务到维修成功包含一系列活动。首先客户需要申请维修（Application），然后在网上进行维修登记（Register）。登记成功后，客户要将自己的设备通过邮寄的形式发送到电脑维修公司（Delivery）。电脑维修公司收到客户的设备后要进行故障检测（Malfunction Detection），设备故障一般包含硬件故障（Hardware Malfunction）和软件故障（Software Malfunction）。两种故障可以都存在，也可以只存在其一，甚至存在无故障的情况，即客户使用环境的问题而非设备本身的问题。对于检测到的设备硬件故障，维修人员要进行硬件维修（Hardware Fix），同样的对于软件故障也要进行软件维修（Software Fix），检测出故障并维修的过程可能多次发生，也可能不发生。所有故障维修200条迹的日志L3，如表1所示。在这些日志中，不包含任意重复活动连续出现的情况，即或这类情况。完毕，有关人员对维修费用进行统计（Expense Statistics），并将客户的设备打包发回给客户（Return）。客户在收到返回的设备后，要进行验收（Check），验收完成后需缴纳维修费用（Pay）。最后电脑维修公司要对客户进行定期回访，短期内跟踪客户的设备使用情况（Follow Up）。

针对该业务流程实例，依据自由单循环完备日志定义，模拟了三组符合自由单循环完备的日志，分别为包含50条迹的日志L1、包含100条迹的日志L2以及包含

表1 三组自由单循环完备日志

根据αfsl算法对表1中的日志进行挖掘得到模型，见图3。由于α算法不支持对短循环结构的挖掘，因此作为对比，分别选取了能够挖掘短循环的α+算法[3]、ILP算法[13]以及IM算法[14]对相同日志进行挖掘，挖掘模型的结果见图4、图5和图6。

图3 αfsl算法挖掘的模型

图5 ILP算法挖掘的模型

图6 IM算法挖掘的模型

依据电脑维修公司的业务流程，可以发现硬件检测出故障与硬件维修同时存在，同样软件检测出故障与硬件维修也同时存在。由于一台设备由多个硬件组成，硬件出现故障的情况有很多，要逐一检测和维修。因此，硬件检测出故障以及硬件维修这两个活动可能多次出现，同样软件检测出故障以及软件维修也会多次出现。对于一台设备，甚至会出现没有故障即客户判断失误的情况，这种情况不会出现软硬件故障以及软硬件维修活动。

对于这几种情况，αfsl算法能挖掘出符合这些情况的工作流模型。根据图3可以看出，硬件检测出故障（Hardware Malfunction）与硬件维修（Hardware Fix）存在于同一个自由单循环结构中，说明每次发现一种硬件的故障，要对其进行维修。对于软件出现故障（Software Malfunction）以及软件维修（Software Fix）同样适用。硬件故障以及硬件维修组成的自由单循环结构与软件故障以及软件维修组成的自由单循环结构处于并发结构中，说明了软硬件的检测和维修能够同时发生，也可以只发生其中一种，甚至可以都不发生。

对于α+算法、ILP算法和IM算法，这三种算法不能正确地挖掘出该业务流程对应的模型。根据图4和图5可以看出，α+算法以及ILP算法挖掘到的模型本身存在错误，硬件检测出故障（Hardware Malfunction）和软件出现故障（Software Malfunction）这两个变迁没有后继库所，硬件维修（Hardware Fix）和软件维修（Software Fix）这两个变迁没有前驱库所，也没有表现出自由单循环结构。根据图6可以看出，对于IM算法挖掘到的模型，硬件故障和硬件维修没有满足必然同时出现的情况，软件故障和软件维修也没有满足该情况，并且没有表现出自由单循环结构。图7和图8分别从各算法在不同日志下挖掘模型的拟合度和精确度的表现给出了实验结果，拟合度检测使用ProM插件Replay a Log on Petri Net for Conformance Analysis，精确度检测使用ProM插件Check Precision based on Align-ETConformance。

图7展示了对于不同日志各算法挖掘模型的拟合度比较。从图中可以发现，对于每个日志，αfsl算法和IM算法挖掘的模型拟合度相同而且很高，而α+算法和ILP算法得到的模型的拟合度较低。

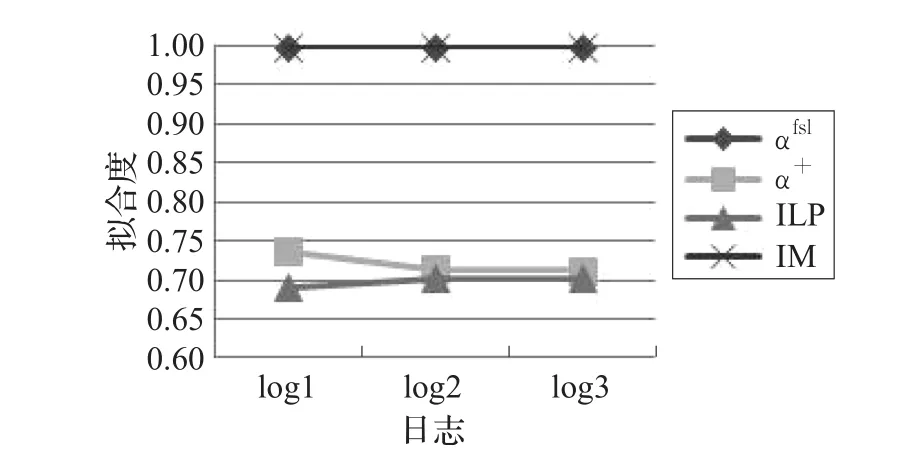
图7 拟合度比较

图8 展示了对于不同日志各算法挖掘模型的精确度比较。从图中可以发现，虽然αfsl算法挖掘的模型随着日志中迹条数的增多精确度略有降低，但仍旧处于较高水平。相比之下，IM算法挖掘的模型精确度较低，而α+算法和ILP算法得到的模型的精确度效果不佳。

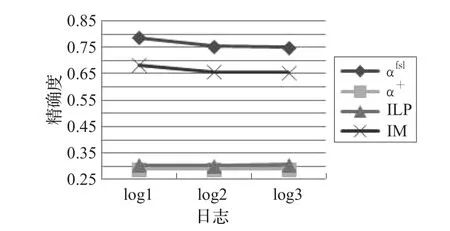
图8 精确度比较

6 结束语

为了挖掘存在于并发结构中的特殊循环结构（自由单循环结构），本文重新定义了存在自由单循环结构的日志完备性，并且基于α算法提出了αfsl算法，针对这种结构进行挖掘。通过实验例证了αfsl算法挖掘的模型具有较高的拟合度和精确度。本文算法仅针对文中定义的自由单循环结构嵌套在并发结构中的情况进行挖掘，对于其他类型的结构，甚至更加复杂的情况，将来会有更进一步的讨论和研究。