严格对角占优Z-矩阵的多级预条件AOR迭代法

薛秋芳，肖燕婷，魏 峰

西安理工大学 理学院 应用数学系，西安 710054

1 引言

科学计算中的很多问题最后都归结为求解线性方程组：

这里，A∈Rn×n是非奇异矩阵；x,b∈Rn，x是未知向量，b是给定的向量。这类方程组一般采用迭代法求解。如果令 A=M-N,其中 M,N∈Rn×n且 M 非奇异，则基本的迭代格式为：

这里，c=M-1b,T=M-1N是迭代矩阵，其谱半径不仅决定了该迭代法是否收敛，还决定了迭代的收敛速度。尽管某些迭代法可求解方程组（1），但很多时候，由于缓慢的收敛速度，求解效率往往很低。

为了改善迭代法的收敛性，研究者们提出了预条件技术[1-18]，即将原方程组（1）转化为预条件形式：

其中，P为非奇异矩阵，被称为预条件子。该方程组的基本迭代格式为：

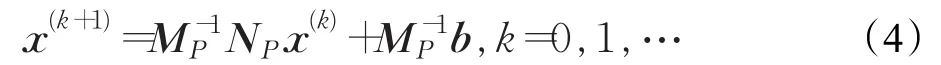
其中，PA=MP-NP,且MP非奇异。迭代法（4）被称为预条件迭代法。

不同的分裂PA=MP-NP可以得到不同的预条件方法，如预条件SOR迭代法、预条件Gauss-Seidel迭代法等。

文献[1]和[2]分别提出了如下两个经典的预条件子：

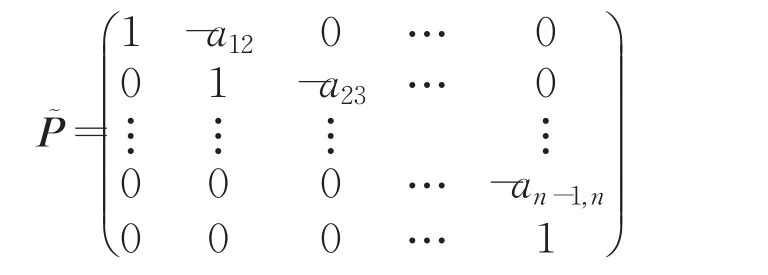
他们研究了预条件Gauss-Seidel迭代法的收敛性。不久之后，文献[3]探讨了带有预条件子P˜的预条件SOR迭代法的收敛情况。

关于文献[1-2]的进一步研究和推广可参考文献[4-5]。另外，Evans等人在文献[6]中提出了预条件子：

并分析了相应的预条件AOR迭代法的收敛性，证明了对不可约L-矩阵，预条件迭代法优于标准迭代法。

受以上预条件子的启发，本文提出一类新预条件子，以上提到的预条件子均为其特殊情况。本文将该预条件子应用于AOR迭代法，从而将上面的预条件方法推广到更一般的情况。

不失一般性，设A=I-L-U ，其中I是n×n单位阵，-L和-U分别是矩阵A的严格下三角和严格上三角矩阵。令：

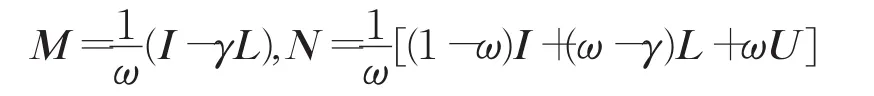
则AOR迭代矩阵为：

其中，ω,γ∈[0,2),(ω≠0)是松弛因子（参见文献[19]）。显然，当 (ω,γ)分别取 (ω,ω)、(1,1)和 (1,0)时，可分别得到SOR迭代矩阵、Gauss-Seidel迭代矩阵和Jacobi迭代矩阵。

下面给出新预条件子。

设i∈S={1,2,…,n-1},定义 A的一类预条件子P(i)为：

这里0≤αj≤1,j=1,2,…,n-i，且存在 j使得

对应于该预条件子的方程组为：

其中：

若令 D(i)、-L(i)和-U(i)分别为 P(i)A的对角严格下三角和严格上三角矩阵，则P(i)A=D(i)-L(i)-U(i)。假设 D(i)-L(i)非奇异，则预条件方程组（7）的AOR迭代矩阵为：

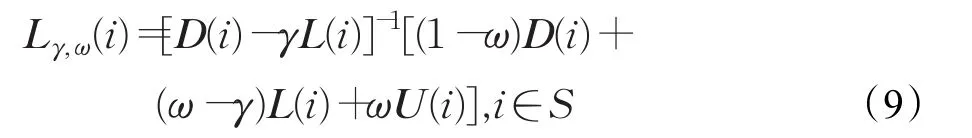
这里ω,γ∈[0,2),(ω≠0)是松弛因子。

若对任意的 j=1,2,…,n-i,αj=0 ，则式（6）中定义的预条件子 P(i)是n阶单位阵，因而式（9）中的 Lγ,ω(i)即为标准AOR迭代矩阵。

本文给出了严格对角占优Z-矩阵的预条件AOR迭代法（带有预条件子P(i),i∈S，简记为PAOR）收敛性分析，并提出了多级预条件AOR迭代法（简记MPAOR），详细研究了这些方法的收敛性。数值算例验证了相关结论，这些预条件子的确提高了原迭代的收敛速度。

2 定义及引理

本文令I表示单位矩阵，ρ(A)表示矩阵A的谱半径。对向量x∈Rn，令x≥0(x＞0)表示x是非负的（正的），即x的每个分量都是非负的（正的）。对向量x,y∈Rn，令 x≥y(x＞y)表示 x-y≥0(x-y＞0)。对矩阵也有类似的约定。

定义1矩阵A=(aij)∈Rn×n被称为：

（1）Z-矩阵，如果对任意的 i≠j,aij≤0。

（2）L-矩阵，如果 A是Z-矩阵且对任意的i=1,2,…,n,aii＞0。

（3）M-矩阵，如果 A=s I-B,其中 B≥0且ρ(B)≤s。

显然，严格对角占优的L-矩阵A一定是非奇异M-矩阵，因此A-1≥0。

定义2设A是实方阵，称分裂A=M-N为：

（1）正规的，如果M-1≥0且N≥0。

（2）弱正规的（第一型弱非负的），如果 M-1≥0且M-1N≥0。

（3）第二型弱非负的，如果M-1≥0且NM-1≥0。

一般地，正规分裂⇒两种类型的弱非负分裂。反之，则不对。

引理1[7]设A是满足A-1≥0的非奇异矩阵。

（1）如果A=M-N是弱非负分裂（第一型或第二型），那么 ρ(M-1N)＜1。

（2）如果A=M-N是第二型弱非负分裂，那么存在向量x≥0且x≠0使得M-1Nx=ρ(M-1N)x且Ax≥0,同时Nx≥0且Nx≠0。

引理2[8]设 A1,A2∈Rn×n,Ai=Mi-Ni,i=1,2是非负分裂。如果Perron向量x2≥0且x2≠0（对应于ρ(T2)的向量 x2）满足 T1x2≤T2x2，那么 ρ(T1)≤ρ(T2)，其中Ti=Mi-1Ni,i=1,2。

引理3[20]设A∈Rn×n是非负矩阵，那么：

（1）ρ(A)是A的一个特征值，如果A是不可约的，那么 ρ(A)＞0。

（2）对特征值ρ(A)存在相应的特征向量 x≥0，且x≠0，被称为Perron向量，如果矩阵 A不可约，那么x＞0。

引理4[20-21]设A是非负矩阵。

（1）如果存在向量 x≥0且 x≠0，使得αx≤Ax,那么α≤ρ(A)。

（2）如果A不可约，并且存在向量x≥0且x≠0使得αx≤Ax≤βx,且等号不成立，那么α＜ρ(A)＜β且x＞0。

（3）α＞ρ(A)当且仅当αI-A非奇异且(αI-A)-1≥0。

3 预条件AOR方法的收敛性分析

下面分两部分对预条件AOR迭代法的收敛性展开具体讨论。

3.1 严格对角占优Z-矩阵的PAOR迭代法

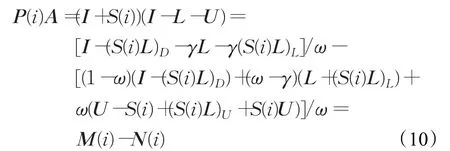
引理5若A=(ajk)∈Rn×n是对角线元素为1的不可约严格对角占优Z-矩阵，则当αj∈[0,1),j=1,2,…,n-i时，P(i)A,i∈S也是不可约严格对角占优Z-矩阵。

证明首先证明P(i)A,i∈S是严格对角占优Z-矩阵。令 B=P(i)A=(bjk)∈Rn×n，则对任意的 j=1,2,…,n-i,k=1,2,…,n且而。因而 P(i)A是L-矩阵，且由和aj,i+j≤0可知：

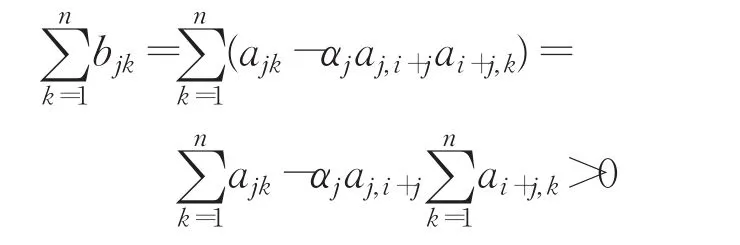
进而P(i)A是严格对角占优Z-矩阵。

下面证明P(i)A,i∈S不可约。显然：

因此，若 ujk≠0，则对 j=1,2,…,n-i，αj∈[0,1)，fjk≠0；若 ljk≠0,则由 (S(i)L)L≥0可知 ejk≠0,再由(S(i)L)U≥0和S(i)U 的非负性，容易得到当αj∈[0,1),j=1,2,…,n-i时，P(i)A是不可约的。

由引理5，分裂（10）是正规的，从而由引理1（1）可知，该分裂是收敛的。

定理1设A是对角线元素均为1的严格对角占优Z-矩阵，Lγ,ω和 Lγ,ω(i)(i∈S)分别是由式（5）和（9）定义的矩阵A的AOR和预条件AOR迭代矩阵，且0≤γ≤ω≤1(ω≠0),则对任意的αj∈[0,1],j=1,2,…,n-i，均有：

ρ(Lγ,ω(i))≤ρ(Lγ,ω)＜1

证明因为A=(I-γL)/ω-[(1-ω)I+(ω-γ)L+ωU]/ω是正规分裂，所以由引理1知 ρ(Lγ,ω)＜1 ，且在向量x≥0(x≠0)，使得 Lγ,ωx=ρ(Lγ,ω)x 并且 Ax≥0。因此：

P(i)Ax=(I+S(i))Ax=Ax+S(i)Ax≥Ax≥0

由S(i)L≥0可知：

M(i)=[I-(S(i)L)D-γ(L+(S(i)L)L)]/ω≤(I-γL)/ω又(I-γL)-1≥0且(M(i))-1≥0，故(M(i))-1≥ω(I-γL)-1,因而：

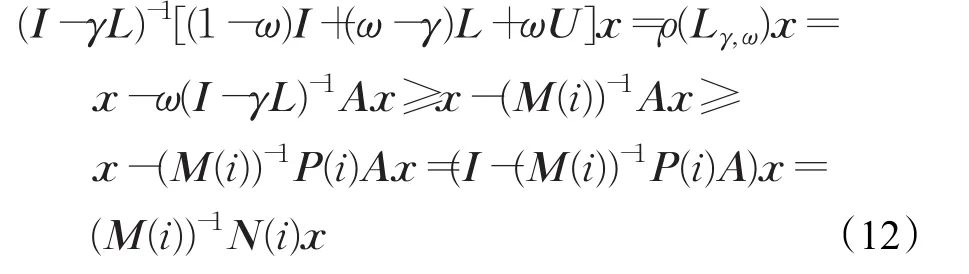
从而，由 (M(i))-1N(i)≥0 及引理2可知 ρ(Lγ,ω(i))≤ρ(Lγ,ω)＜1 。

注1（1）定理1表明当0≤γ≤ω≤1(ω≠0)时，严格对角占优Z-矩阵的预条件AOR迭代法是收敛的，且无需条件 ρ(Lγ,ω)＜1 ，对任意的 i∈S ，均有 ρ(Lγ,ω(i))≤ρ(Lγ,ω)＜1 成立。

（2）在定理1中，选择特殊的ω和γ即可得到，当A为严格对角占优Z-矩阵时，对任意的i∈S均有ρ(Lω(i))≤ρ(Lω)＜1，ρ(G(i))≤ρ(G)＜1 且 ρ(J(i))≤ρ(J)＜1 ，这里 Lω、G 、J和 Lω(i)、G(i)、J(i)分别为 A的SOR、Gauss-Seidel和Jacobi迭代矩阵以及相应的预条件迭代矩阵。

定理2设A是对角元素为1的不可约严格对角占优L-矩阵，Lγ,ω和 Lγ,ω(i)(i∈S)分别是由式（5）和（9）定义的矩阵 A的AOR和预条件AOR迭代矩阵，且0≤γ≤ω≤1(ω≠0,γ≠1)，则对任意的 αj∈[0,1),j=1,2,…,n-i且 αj不全为0，均有 ρ(Lγ,ω(i))＜ρ(Lγ,ω)＜1 。

证明由式（5）和引理4（3）可知下面的等式成立：

其中T≥0。因为A不可约，所以当0≤γ≤ω≤1(ω≠0,γ≠1)时，(1-ω)I+ω(1-γ)L+ωU 也不可约。又T≥0，容易得到 Lγ,ω不可约。

由引理5知当αj∈[0,1),j=1,2,…,n-i时，P(i)A是不可约严格对角占优L-矩阵，因而 M(i)非奇异，Lγ,ω(i)是定义好的，与上面类似可证Lγ,ω(i)不可约。

由引理1的证明过程可知，存在向量x≥0且x≠0使得 (M(i))-1N(i)x≤ρ(Lγ,ω)x（见式（12））。从而，由 αj不全为 0，j=1,2,…,n-i及引理 4（2）可得 ρ(Lγ,ω(i))＜ρ(Lγ,ω)＜1 。

由定理2，类似的结论对SOR和Jacobi迭代法也成立，这里不再列出。

3.2 严格对角占优Z-矩阵的MPAOR迭代法

本节讨论多级预条件AOR方法。

显然，可将预条件子P(i),i=1,2,…,n-1,逐步应用于方程组。对任意的i∈S，令U(i)=P(i)…P(1)，用U(i)左乘以方程组（1）可得：

该方程组等价于（1）。因而方程组（1）的多级预条件AOR迭代法，即方程组（13）的AOR迭代法可由如下的迭代格式定义：

为了方便，记Q(i)=[D(i)]-1，且对任意的i=2,3,…,n-1,B(i)=P(i)B(i-1)Q(i),而 B(1)=P(1)AQ(1),则式（13）可转化为如下等价形式：

将AOR迭代法应用于方程组：

基于引理5和定理1、定理2的分析，容易得到关于多级预条件AOR迭代法的如下结论。

定理3设A是对角线元素均为1的严格对角占优Z-矩阵，Lγ,ω和分别是矩阵 A的AOR和多级预条件AOR迭代矩阵，且0≤γ≤ω≤1(ω≠0)，则对任意的αj∈[0,1],j=1,2,…,n-i,均有：

证明由引理5可知，对任意的i∈S,U(i)A均为严格对角占优Z-矩阵。因为方程组U(n-1)Ax=U(n-1)b可以通过对Ax=b依次左乘P(i),i=2,3,…,n-1得到，所以由定理1知，对任意的 i=1,2,…,n-1均有其中,故：

注2（1）定理3表明对任意的 j=1,2,…,n-i，当αj∈[0,1]时，严格对角占优Z-矩阵的多级预条件子能够逐步加快AOR迭代法的收敛速度。

（2）在定理3中选择特殊的参数可得类似的结论对SOR、Gauss-Seidel和Jacobi迭代法也同样成立。

定理4设A是对角元素为1的不可约严格对角占优Z-矩阵，Lγ,ω和分别是 A 的AOR和多级预条件AOR迭代矩阵，且0≤γ≤ω≤1(ω≠0,γ≠1)，则对任意的 αj∈[0,1),j=1,2,…,n-i且 αj不全为0，均有：

4 数值算例

考虑具有Dirichlet边界条件的二维对流扩散方程：

其中，Ω=(0,1)×(0,1);ξ和σ是常数；∂Ω为Ω的边界；是给定的函数。令步长为使用五点差分格式将方程（14）离散化，得到系数矩阵：

表1 AOR及预条件AOR迭代法的迭代次数、CPU运行时间、谱半径及误差等

图1 （预条件）AOR迭代矩阵谱半径曲线

这里n=N2,T是N×N 是三对角矩阵，即T=tridiag(η1,μ0,μ1),其中：

显然当ξ、ζ和σ取不同值时，会得到不同矩阵。

令初始向量为零向量，迭代终止条件为：

其中ε=h2/5，而b是使得线性方程组的精确解为(1,1,…,1)T∈Rn的向量。

在此方程组中，令ξ=ζ=σ=0,并分别应用AOR迭代法、预条件AOR迭代法（PAOR）及多级预条件AOR迭代法（MPAOR）求解。在表1中，令ρ表示相应迭代矩阵的谱半径。对任意的 j,α=αj=0.5,ω=0.9,γ=0.7。

以下实验均使用MATLAB程序完成。

由表1可见，无论是迭代次数、求解速度，还是谱半径，PAOR方法明显优于AOR迭代法，而MPAOR迭代法则是这三种方法中收敛最快的方法。该例表明，相比标准的AOR迭代法，预条件AOR迭代法较大地加快了方程的求解速度，而多级预条件AOR迭代法则可进一步提高预条件方法的收敛速度。

图2（预条件）SOR迭代矩阵谱半径曲线

图1 和图2分别是相应的AOR和SOR迭代法的谱半径曲线。图1给出了当γ=0.01,ω∈(0.01,1)时，AOR、PAOR和MPAOR迭代法的谱半径曲线。图2给出了当ω∈(0.01,1)时，SOR、PSOR和MPSOR迭代法的谱半径曲线。

由图1可见，文中迭代法谱半径由小到大的排列顺序依次为MPAOR、PAOR和AOR，由图2可见，类似的结果对相应的（预条件）SOR迭代法也成立。