一道数学探究题的教学与思考

☉安徽省淮北市第一中学 牛 松

☉淮北师范大学附属实验中学 闫 寒

一、原题再现

题目 已知一个函数的解析式为y=x2，它的值域为［1，4］，这样的函数有多少个？试写出其中两个函数.

这是一道开放题，有无数个不同的答案，为了更好地体现学生的主体性地位，笔者先让学生自己独立思考，让学生尽可能多想几个答案，同时，在教室来回巡视.巡视过程中看到好多同学都有了答案，有的还不止两个，而且不同的学生的答案是不同的.于是笔者又让学生把自己的想法在小组内相互交流，相互启发，共同解决问题.

小组讨论结束后，让每组选出代表汇报成果，其他组可以补充.

组1：我们觉得函数的解析式是不变的，关键是定义域可取不同的范围.如x∈［1，2］，x∈［-2，-1］.

师：你是怎么得到这两个函数的？

组1：猜的，把两个端点1，2或-1，-2代入得函数值分别为1和4.

师：很好，猜想也是一种数学思想方法.但它不是很严密的，需要进一步论证.如果把两端点代入得到1和4即可的话，那么当x∈［-2，1］时，是否也满足条件？

（这时马上有同学示意要求发言）

组2：不对，如果把0代入，则函数值为0，不在值域范围内.

这时另有学生在底下嘀咕：画图也可以看出来.

师：对，数形结合是解决函数问题很重要的思想方法.通过分析图像，能不能验证一下第1组同学的答案的正确性？

组3：由图像可知，这两个区间对应的函数值是连续的，且1和4分别为函数的最大值和最小值，所以组1的答案是正确的.但若x∈［-2，1］，则值域为［0，4］，所以不满足条件.

师：回答得非常好！同学们通过数形结合的方法验证了答案.那么，还有没有别的符合条件的函数了呢？

（说到这里，笔者发现有的组突然沉默下来，而有的

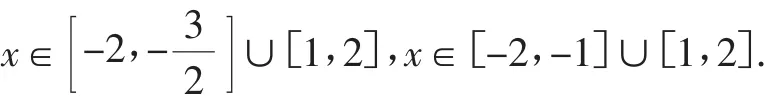
这位同学的观点似乎把刚才处于思维盲区的部分同学的思路一下子打开了，不少同学的脸上露出了会心的微笑……

组5：我们也发现了这个特点，而且觉得满足条件的函数有无数个.

笔者抓住机会继续问：“这无数多个函数的定义域都要满足什么条件？有没有什么规律？”

组5：发现了一些，如x∈［-2，-1］∪A，则A［1，2］；如x∈［1，2］∪B，则B［-2，-1］.

一些同学听了，投去了崇拜的目光，又透露出不服输的表情，绞尽脑汁地想着其他可能的情况.

经过一阵的小组讨论，终于有学生举手发言.

组6：也可以这样写，x∈［-2，a］∪［1，b］且-2≤a≤-1，1≤b≤2，|a|≤b.

组7：也可以这样写，x∈［c，-1］∪［d，2］且-2≤c≤-1，1≤d≤2，|c|≥d.

师：刚才三组同学分析出了可能的几种情况，通过这些情况的研究，谁能最后总结出隐含的规律呢？

热闹的教室一下子安静了下来，同学们陷入沉思之中……

过了一会儿，有一位学生自告奋勇站了起来.

生1：我觉得这两个集合应满足：（1）在y轴的两侧；（2）负数集合中元素的绝对值所构成的集合与正数集合的并集应为［1，2］，这样函数的值域一定为［1，4］.

师：概括得非常好！只要满足这两个条件的集合的并集所对应的函数即为所求函数.

（这时，笔者看到有一位男生欲言又止）

师：有没有同学还想补充？

生2：定义域能否可以由三个集合的并集构成呢？组的同学似乎有点兴奋，笔者立刻给予他们发言的机会）

师：你们有需要补充的吗？

组4：我们觉得可以把定义域写成两个集合的并集的形式.比如：

“一石激起千层浪”，同学们的情绪更加高涨了.笔者似乎能感觉到有部分同学心里在想：是呀！我怎么没想到呢？

笔者及时表扬了该生的钻研精神，同时又把疑问抛给全班同学：谁来接招？

有了刚才两个集合的探讨，有部分同学已领悟了实质，所以没过一会儿就有学生举起了手.

生3：也可由四个、五个甚至更多的集合的并集构成，只要满足负数集合中元素的绝对值组成的集合与正数集合的并集为［1，2］.

师：真棒！能否总结一下：若y=x2，它的值域为［n，m］，n，m∈R*，这样的函数有多少个？它的定义域有何特点？

生4：这样的函数有无数个.定义域可由任意个集合的并集构成，且这些集合的绝对值的并集为

至此这道题的教学基本任务已完成，如何对习题进行必要的整合从而挖掘习题的最大功效是新课改的一个必要环节.

师：刚才老师在巡视时，发现有同学把值域为［1，4］看成{1，4}，所以他求出的两个函数的定义域分别为{1，2}，{-2，-1}.如果这道题的值域就改为{1，4}，那么这样的函数共有多少个？它的定义域有何特点？

生5：这样的函数有两个，定义域分别为{1，2}，{-2，-1}.

生6：定义域还可能为{-1，2}，{-2，1}.

师：大家不要轻易下结论，总结归纳一下，到底有几个？

生6：定义域可以为{1，2}，{1，-2}，{-1，2}，{-1，-2}，{1，-1，2}，{1，-1，-2}，{1，-2，2}，{-1，-2，2}，{-1，1，-2，2}，共九种情况.

师：总结上面的结论，有何规律？

生7：定义域分别是从{1，-1}和{2，-2}中任取一个或两个元素所组成的集合.可分为两步，每步的种数与求含两个元素的集合的非空子集的个数一样，即（22-1）×（22-1）=3×3=9（个）.

师：若y=x2，它的值域为{1，4，9}，这样的函数的定义域有多少种情况？

生8：定义域分别是从{1，-1}和{2，-2}和{3，-3}中任取一个或两个元素所组成的集合，共3×3×3=27（种）.

师：若y=x2，它的值域中含n个元素（不含0），那么定义域有多少种情况？

生9：3n（种）.

师总结：这节课我们从一道课本习题出发，研究了与之有关的一些问题，推广到一般，得出了一些有用的结论.同学们在做题时，要学会分析研究、归纳总结题中隐含的丰富的数学规律，拓宽思路，自主探究问题的解决途径，不断提高自己的数学素养.课后，请同学们思考这样的几个问题：

（1）若函数y=f（x）关于x=a（a∈R）对称，值域为［n，m］（m>n>f（a）），这样的函数的定义域有何特点？

（2）若函数y=f（x）关于x=a（a∈R）对称，值域为［n，m］（n

（3）若函数y=f（x）关于x=a（a∈R）对称，值域为{m1，m2，m3，…，mn}（n∈Z*），这样的函数的定义域有多少种情况？

二、一点思考

1.传统教学模式下学生的一些不足状况

传统的教学方法以教师讲、学生听的注入式教学占主导地位.这种教学模式随着改革开放，凸现出其不足.表现在学生应用数学的意识不强，创造能力较弱.学生不能把实际问题抽象成数学问题，不能把所学数学知识应用到实际问题中；学生机械地模仿一些常见数学问题解法的能力较强，而当面临一些新的问题时却办法不多，对于诸如观察、分析、归纳、类比、抽象、概括、猜想能力较差.

2.新课标下的数学课堂教学

新颁布的《全日制义务教育数学课程标准》（实验稿）的基本理念指出：“学生的数学学习活动不应只限于……还应倡导自主探究、合作交流等学习数学的方式.通过各种不同形式的自主学习、探索活动，让学生体验数学发现和创造的历程.”在新课标的实施建议中也建议数学课堂中“既要有教师的讲授和指导，也有学生的自主探究和合作交流，教师要创设适当的问题情景，鼓励学生发现数学的规律和问题的解决途径，使他们经历知识形成的过程”.

作为一线的教师不但要关注新一轮课改的新理念，体会新课标、教材的指导思想和改革重点，更要想方设法把它们落到课堂教学的实处.

3.新课改下教师的专业化

教师的专业包括教育和数学两个方面.从教育素养看，一方面，使学生学到知识的同时“学会学习”，形成热爱知识、乐于学习的心里倾向；另一方面，通过自己的“言传身教”培养学生积极向上的人生观、价值观.从数学素养看，要使学生在打好“双基”的基础上，学会“数学地思维”，形成理性精神.H