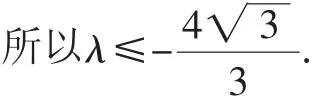妙解例题看数学建模的应用

☉山东省肥城市泰西中学 李家鑫

数学建模是高中阶段数学核心素养的一大内容，也是数学教学与学习过程中必备的技巧技能，其是对现实问题进行数学抽象，用数学语言表达问题、用数学知识与方法构建模型解决问题的素养.数学建模主要包括：在实际情境中从数学的视角发现问题、提出问题，分析问题、建立模型、求解结论、验证结果并改进模型，最终解决实际问题.

一、建立函数与方程模型

例1若二次函数f（x）=ax2+bx+c（a>0）在区间［1，2］上有两个不同的零点，则

分析：常规的方法是根据二次方程根与系数的关系、函数与方程的转化建立起相应的不等式组，利用线性规划来处理.而涉及二次函数已知零点的分布求解参数的取值范围问题时，可以采用使用二次函数的零点式模型的建立，将参数化归为零点组合式的取值范围问题，结合题目条件加以转化与应用即可.

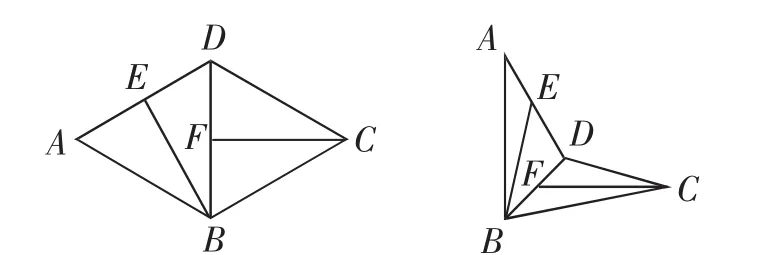
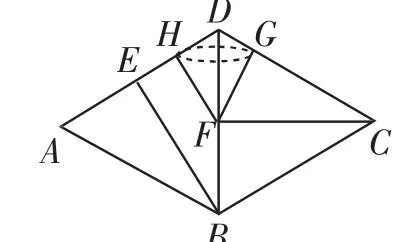
解：设二次函数f（x）=ax2+bx+c（a>0）在区间［1，2］上的两个不同的零点分别为x1，x2，其中1≤x1

点评：巧妙借助二次函数的零点式的数学模型的建立，代入对应的关系式，结合不等式的性质来确定相应关系式的取值范围.处理起来更直接，解决问题更直观.建立模型直观有效，且更切入实质，达到快速解决问题的目的.

二、建立平面几何模型

例2（2018届江苏省南师大附中、淮阴中学、海门中学、天一中学高三2月联考·14）已知a>1，b>2，则的最小值为______.

分析：常规的方法是通过引入参数，结合基本不等式、导数、待定系数法等思维来分析，解答过程比较繁杂.而通过构造平面几何模型，数形结合再利用基本不等式来处理，非常简单有效，直观易懂.

解：由于a>1，b>2，如图1，构造平面几何模型，记h=|CD|=>0，则（a+b）2≥|CE|2=|CD|2+|DE|2=h2+（1+2）2=h2+9.

图1

故所求最小值为6.

点评：根据题目的条件建立相应的平面几何概型，通过两个直角三角形的关系，结合三角形的性质或三角函数的最值，可以达到“秒杀”的效果.对平面几何模型的构造必须具有非凡的想象力与创新力.

三、建立平面向量模型

分析：常规的方法是结合相应的关系式的变形与转化，利用基本不等式、不等式的性质或柯西不等式等来解决最值问题.而通过建立平面向量，利用平面向量的数量积公式的性质来转化，可以有效地进行放缩达到确定最值的目的.

解：根据平面向量数量积的性质（m-n）2=m2+n2-2m·n≥0，可得2m·n≤m2+n2.

设平面向量m=（a，1），n=（1，b），可得2（a+b）≤a2+1+1+b2=a2+b2+2.

故所求最小值为2.

点评：借助平面向量模型的建立，根据平面向量数量积的性质（m-n）2=m2+n2-2m·n≥0，即2m·n≤m2+n2，通过设出对应的向量加以应用，进而对相应的分母进行放缩法处理，达到两者同分母，结合分式的运算加以确定双变元代数式的最小值问题.模型建立比较常规，解决问题有效.

四、建立立体几何模型

图2

分析：常规的方法是根据异面直线的定义，结合定义、向量、坐标法等思维来解决问题，从而达到解决平面图形折叠与转化的目的.而借助立体几何模型，先作出辅助线，确定HF与CF所成的夹角就是异面直线BE与CF所成的角，根据翻折时HF所对应的立体几何模型的特征，结合圆锥的性质来确定两直线的夹角问题，从而求解异面直线所成的角.

解：如图3，过点F作FH∥EB交AD于点H，则HF与CF所成的夹角就是异面直线BE与CF所成的角.

图3

将△ABD沿对角线BD翻折时，HF所对应的轨迹恰好是以HG（G为DC上靠近D点的四等分点）为底面圆直径、DF为对称轴的圆锥的母线.

结合模型可知，母线位于HF或GF时，此时HF与CF所成的夹角为，母线位于CF的垂面上时，此时HF与CF所成的夹角为.

点评：在解决立体几何的翻折问题时，在翻折过程中，有些量是不变的，而有些量是改变的，直接处理起来难度比较大.而借助立体几何模型，以直观的形式来解决平面、旋转、折叠等问题，通过直观立体几何模型来分析，很好地达到目的.

五、建立解析几何模型

例5 在△ABC中，角A，B，C的对边分别为a，b，c，若sinA+sinB+λsinAsinB=0，且a+b=2c，则实数λ的取值范围是______.

分析：常规的方法是结合正弦定理、三角恒等变换公式等来转化与应用，达到求解参数的取值范围.求解思路较一般，过程繁杂.而通过条件a+b=2c建立点C的轨迹方程——椭圆，利用椭圆的几何性质来处理与解决，更为直观快捷.

解：如图4，以A，B为焦点，且满足a+b=2c的点C的轨迹方程是椭圆，其对应的标准方程为

图4

当C趋近于长轴的顶点时，此时h→0，λ→-∞.

点评：特殊在解决一些代数问题、三角问题中，涉及定和、定差、定距离等问题，经常建立与之相关的椭圆、双曲线、圆的轨迹，利用解析几何模型来处理，往往可以有效利用解析几何知识来转化，达到有效处理与解决问题的目的.

数学建模能积极有效地启发学生的创新性思维，开启学生的智力发展，用科学的方法将凌乱的知识系统化、深入化、拓展化，从而在提高学生的思维能力与思维品质方面表现出独特的效果，真正培养学生的创新思维，增强创新意识和科学精神，提升数学能力与数学素养.H