基于风洞试验俯仰运动的分段式速度控制

苏晓兵，林敬周， 王 雄， 谢志江

(1.重庆大学 机械传动国家重点实验室, 重庆 400044；2.中国空气动力研究与发展中心超高速所， 四川 绵阳 621000)

风洞捕获轨迹试验(Captive Trajectory System，CTS)是一种先进且复杂的特种试验技术，主要是测量具有动力系统的外挂物与载机分离后的运动轨迹，以此来评估外挂物与载机的安全分离特性，为外挂物在载机上的合理布局、安全分离所需参数提供试验依据[1-2]。美国从20世纪50年代开始该技术的研究，英国、法国从20世纪70年代开始该技术的研究与应用。中国空气动力研究与发展中心于1980年利用1.2 m跨超声速风洞研制了第1套高速风洞捕获轨迹试验系统，并于1988年正式投入使用，完成了大量的型号试验，对我国飞行器技术的发展作出了重要贡献[3]。

设计某风洞捕获轨迹试验系统时，提出一种以六自由度串联机构支撑外挂物模型并由计算机系统进行运动控制的实现方案。对俯仰机构进行设计时，考虑风洞试验中机构阻塞度影响[4]、机构运动特性以及响应速度等因素，提出一种直线变圆弧机构代替旋转副以实现捕获轨迹系统的俯仰运动。由于此俯仰机构输入端与执行端的非线性关系，使得此俯仰机构速度控制成为一大难点。很多学者对速度控制方法进行了研究，当前常见的速度控制方法有[5-6]直线加减速法、指数加减速法、多项式加减速法、抛物线加减速法、S曲线加减速法等。这些方法都包括加速、匀速、减速过程，它们的研究重点是加减速过程，而对于匀速过程，主要针对的是驱动端或者线性控制系统执行末端的匀速控制。本文主要研究如何保证非线性控制系统机构执行末端的速度控制精度。进行俯仰单自由度运动连续测力模式试验[1]时，运动角速度控制采用的常规方法为：根据俯仰运动范围逆解得到直线滑块运动起止点位置，然后通过起止点一次性完成电机速度的规划。在此种速度控制方法下俯仰运动角速度存在很大误差，且误差会随运动角速度的增大而急剧增大。为此，提出一种分段式速度控制方法：对俯仰运动范围进行分段处理，依次以各段为单元来进行电机速度的规划，从而保证整个俯仰运动范围中的角速度精度。基于分段式速度控制方法的理论基础，搭建了相应控制系统进行俯仰运动试验，试验结果验证了该方法的可行性。

1 俯仰机构运动学分析

俯仰机构结构如图1所示，主要由伺服电机、联轴器、丝杠螺母、直线导轨滑块、驱动连杆、弧形导轨滑块、直线滑块安装座等构成。

1.伺服电机；2.联轴器；3.丝杠螺母；4.丝杠；5.直线滑块；6.驱动连杆；7.直线导轨；8.弧形导轨；9.弧形滑块安装座；10.尾部部件；11.滚转机构

图1 俯仰机构模型

机构工作原理：伺服电机通过联轴器驱动丝杠旋转使得丝杠螺母作直线平移运动，与丝杠螺母固连的直线滑块带动驱动连杆一端沿着直线导轨运动，驱动连杆另一端则带动弧形滑块安装座、尾部部件和滚转机构沿弧形导轨绕弧形导轨圆心进行旋转运行，从而使得机构末端实现俯仰运动。

1.1 机构运动学逆解分析

俯仰机构运动简图如图2所示，以圆弧导轨圆心为原点建立直角坐标系Oxy。驱动连杆长度为L，弧形导轨半径为R。设定直线导轨的安装平行于x轴且与原点O距离为y0。A、B为机构末端俯仰角α=0°时直线滑块和弧形滑块的位置，此时BO与y轴夹角为θ。A′、B′为机构末端俯仰角转动任意位置后直线滑块和弧形滑块位置，直线滑块由A运动到A′的距离为S，运动角度∠BOB′即为机构末端运动俯仰角α。

图2 俯仰机构运动简图

当俯仰角α=0°时，设A坐标为A(x0,y0)，此时B坐标为B(R·sinθ,R·cosθ)。当俯仰角转动任意位置后，则A′坐标为A′(x0+S,y0)，B′坐标为B′(R·sin(θ+α),R·cos(θ+α))。

根据封闭矢量法建立矢量方程组：

(1)

化简得：

(2)

由几何关系得：

(3)

解得直线滑块位移S与俯仰角α关系式：

S=R(sin(θ+α)-sinθ)+

(4)

由式(4)可得直线滑块运动位移S只与机构俯仰角α有关，因此能很容易地实现俯仰运动的位置控制。

设f(α)为根据俯仰角α逆解的直线滑块绝对位置，根据式(3)(4)可得：

f(α)=x0+S

(5)

将式(5)两边同时对时间求1阶导数可得：

(6)

通过式(6)可得直线滑块速度v与俯仰角速度ω关系

v=(cos(θ+α)+

(7)

由式(7)可知，直线滑块运动速度v同时取决于ω和α两个参数。由于v=dS/dt，故要保证v与α时刻都满足式(7)是无法实现的。风洞试验中，必须保证的是机构运动的位置精度，而运动速度允许存在一定的偏差。当然，运动速度越接近设定值，则越能保证风洞试验结果的准确性。

1.2 俯仰机构运动学正解分析

当已知直线滑块运动规律后，需要求解俯仰机构实际的旋转运动规律，故需对俯仰机构进行正解分析。由式(2)可得：

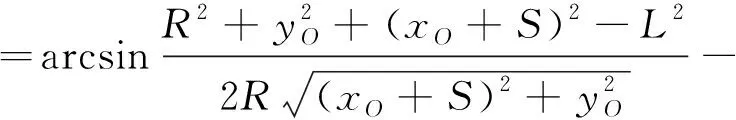
(8)

将式(8)两边同时对时间求1阶导数可得：

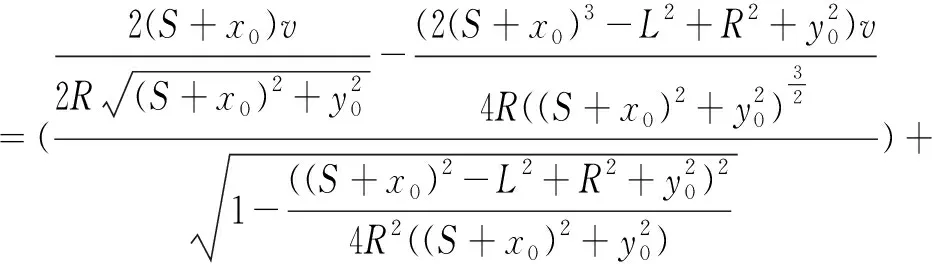
(9)

2 俯仰运动分段式速度控制方法

2.1 俯仰运动常规速度控制方法

俯仰运动常规速度控制方法：根据俯仰运动范围逆解得到直线滑块运动起止点位置，通过起止点一次性完成电机速度的规划。整个运动过程中保证v为定值，而ω则不断变化。

风洞试验中俯仰运动范围为[-20°,+20°]，运动角速度ω最大值为10 (°)/s。在Matlab中进行如下仿真：分别在俯仰角速度为1、5、10(°)/s的情况下使机构从-20°位置运动到+20°位置，记录实际运动角速度并处理得到角速度误差值。仿真结果如图3所示。

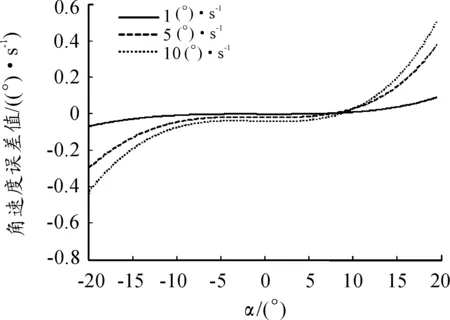
图3 常规方法下3种速度仿真结果

由仿真结果可得：

1) 俯仰运动位置越接近正负极限，俯仰角速度误差值越大。

2) 随着俯仰目标角速度的增加，误差也随之增大。

2.2 俯仰运动分段式速度控制方法

2.2.1 分段式速度控制方法步骤

针对常规速度控制方法中角速度误差较大的问题，提出分段式速度控制方法，其速度控制示意图如图4所示，具体步骤如下：

1) 获得当前俯仰角和目标俯仰角位置，分别设为αstart、αend。

2) 从αstart开始，用Δα对整个运动范围[αstart,αend]进行分段处理，设整个范围共划分成了N段，节点分别为α1、α2、…、αN。分段结果包括以下几种情况：

① 若(αend-αstart)为Δα的整数倍，则αi=αstart+i·Δα(i=1,2，…,N)。

② 若(αend-αstart)不为Δα的整数倍，则

③ 若(αend-αstart)小于Δα，则αN=α1=αend。

3) 根据给定俯仰运动角速度ω计算每段运动完成时间t：

(10)

4) 以S=F(α)表示式(4)方程，逆解αi对应的直线滑块位置Si(i=0,1,2，…,N)：

(11)

5) 规划直线滑块从Si-1到Si区段的速度，根据式(10)(11)计算各段中直线滑块速度vi：

,i=1,2,…,N

(12)

6) 以五次多项式[7-8]规划vi到vi+1的过程使Si-1到Si实现速度平滑过渡。

图4 分段式速度控制示意图

2.2.2Δα取值研究

Δα越小，俯仰机构末端实际运动角速度越精确，但控制程序运算时长会随之增大，控制程序运算时长越大则系统的实时性越差。故需要确定一个合理的Δα，能同时兼顾角速度运动精度和系统的实时性。由本文2.1节可知，角速度越大则角速度误差值越大，为保证所有速度下Δα都能适用，选取运动角速度为10(°)/s，运动范围为[-20°,+20°],测量各Δα对应的角速度最大误差值。另外，在同一台电脑上得到各Δα对应的控制程序运算时长，结果如表1所示。

由表1可得：当Δα为0.4°时，速度误差值能满足风洞试验控制要求，且程序运算时长也较短。故选择Δα值为0.4°。

表1 各Δα对应角速度最大误差及程序运算时长

3 试验系统的搭建与结果分析

3.1 试验系统硬件架构

试验系统采用基于PC的控制技术和高速以太网总线EtherCAT技术相结合的网络化控制系统方案，其硬件系统拓扑图见图5。

1.工控机；2.EtherCAT网线；3.驱动器；4.伺服电机；5.IO模块；6.位移传感器

硬件系统主要组成部分包括：1台高性能工控机，用于控制整套俯仰机构运动控制系统；1台驱动器和1台高精度伺服电机，用于精确控制直线滑块的运动位置和速度；1套IO模块和1套位移传感器，用于检测弧形滑块在弧形导轨上的位置。系统采用高速的EtherCAT现场总线，使得伺服电机驱动控制单元、IO模块采集单元能快速可靠地与工控机之间进行数据传递。

3.2 试验系统软件实现

俯仰机构运动控制程序在基于Windows系统的TwinCAT软件[9-10]开发平台上编写调试完成。TwinCAT软件可将基于PC的Windows系统转换为一个集成PLC、NC和HMI于一体的实时控制系统，其编程风格友好，可靠性强。俯仰运动控制流程如图6所示。

图6 俯仰运动控制流程

3.3 试验结果与分析

按本文设计内容完成试验控制系统硬件的搭建和控制程序的编写，并在程序中配置硬件参数，设置驱动器脉冲当量、丝杠导程和减速比，将电机编码器数值转换为丝杠螺母的直线位置。试验调试现场如图7所示。

图7 试验调试现场

试验内容如下：为全面验证分段式速度控制方法的可行性，控制俯仰机构分别进行慢速、中速、快速运动。分别在角速度为1、5、10 (°)/s情况下进行试验，记录伺服电机编码器反馈的直线滑块速度，逆解得到实际角速，并计算其中速度稳定后的实际角速度与设定角速度的差值。分段式速度控制方法的3种角速度误差见图8～10。分段式速度控制方法和常规速度控制方法的3种角速度误差最大值见表2。

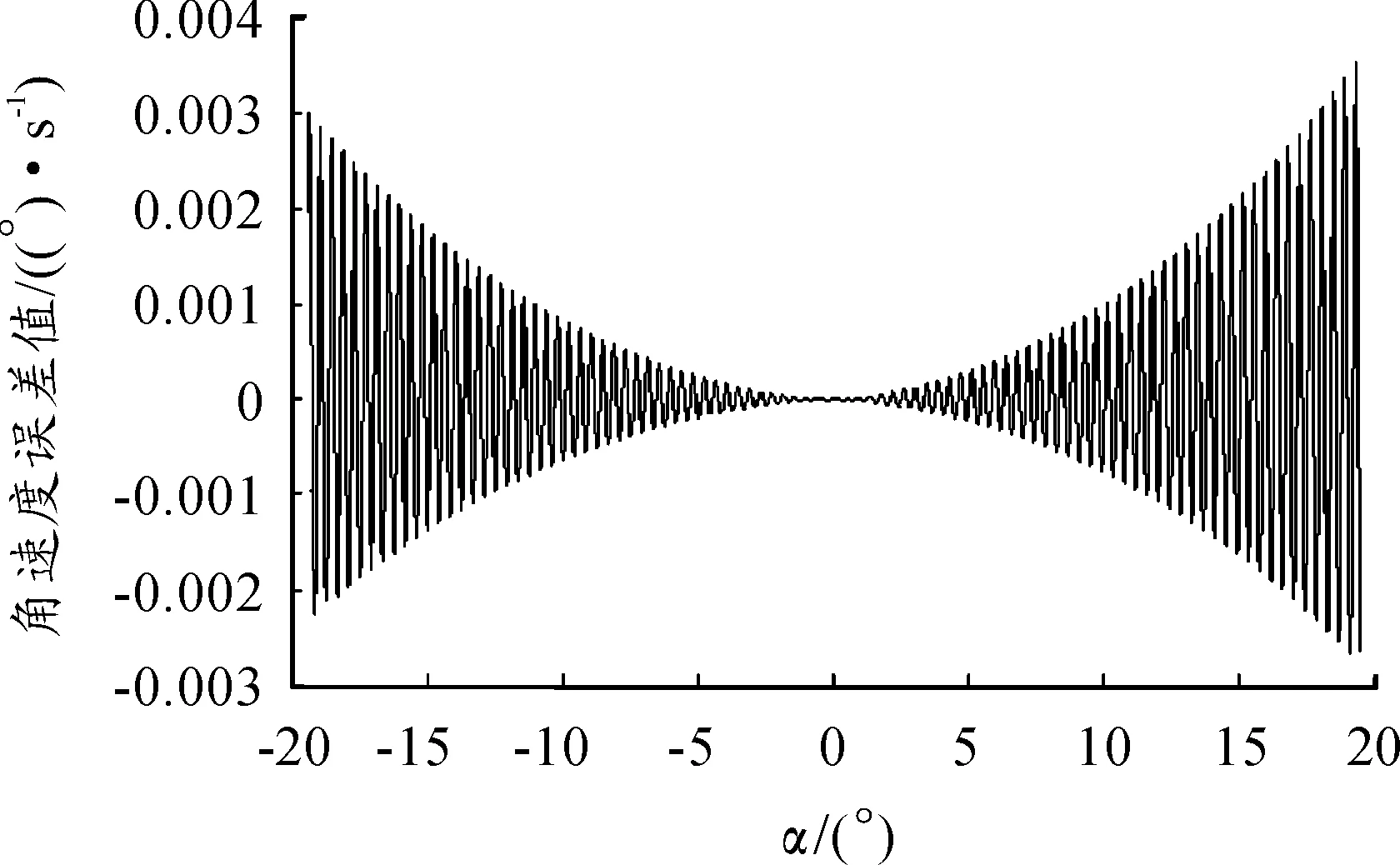
图8 1 (°)/s时角速度误差

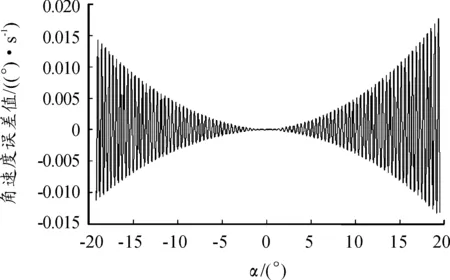
图9 5 (°)/s时角速度误差

图10 10 (°)/s时角速度误差

试验结果表明：分段式速度控制方法的3种角速度误差曲线形状相似，俯仰运动位置越接近正负极限，角速度误差值越大，且角速度误差最大值随运动角速度的增大而增大。各种目标速度下，分段式速度控制方法的角速度运动精度都远高于常规速度控制方法。另外，由于当角速度为10(°)/s时，角速度误差最大值为0.028(°)/s，故其他速度情况下角速度误差都将小于此值。因此，此分段式速度控制方法能有效地减小俯仰运动角速度误差。

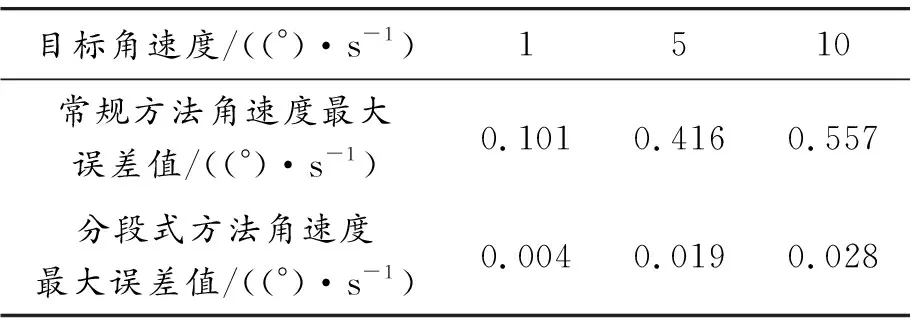
表2 2种方法在各速度下角速度最大误差值

4 结束语

通过对直线变圆弧俯仰机构进行运动学分析，推导了俯仰运动逆解方程，为整个系统位置和速度控制奠定基础。

分析了常规速度控制方法下角速度误差特点，提出了分段式速度控制方法，并通过综合比较角速度误差大小和控制系统实时性选择了合理的段长Δα。

搭建基于PC控制技术和高速以太网总线EtherCAT技术相结合的控制系统硬件平台，并以TwinCAT软件为开发平台编写俯仰运动控制程序。分别以慢速、中速、快速进行俯仰运动试验，记录伺服电机编码器反馈的直线滑块速度并正解得到俯仰运动角速度，通过数据处理得到运动角速度误差值。对比各种目标速度下分段式速度控制方法和常规速度控制方法角速度的最大误差值，可见分段式速度控制方法能很好地保证俯仰运动角速度的精度。

通过对试验结果进行分析可见，分段式速度控制方法能很好地保证俯仰运动角速度精度。另外，本方法还可用于其他类似的非线性速度控制方式中，具有一定的工程实用价值。