正辛烷和1-辛烯在CeY分子筛上吸附的分子模拟研究

任卓然，李 强，秦玉才，宋丽娟

(辽宁石油化工大学辽宁省石油化工催化科学与技术重点实验室，辽宁 抚顺 113001)

石油的重质化趋势使得其深度加工技术的重要性不言而喻[1]。催化裂化是目前常用的重油轻质化技术[2-3]。在重质油催化裂化过程中，C8以上的烷烃和烯烃都是十分重要的催化裂化原料[4]。其在催化剂上吸附扩散行为决定了催化裂化的效果，所以对大分子烃类在催化剂上吸附行为的研究显得尤为重要。

前人的研究较多关注重油催化裂化过程中重油组分的变化，以及烷烃、烯烃含量对辛烷值等性能指标的影响[5-6]。为了提高这些指标，不少的研究者对催化剂本身进行了大量的研究，包括新材料的合成和既有催化剂的改性，其中Ce离子改性的Y分子筛是很好的催化裂化催化剂。大量实验研究表明Ce离子引入Y分子筛中，Ce离子是以Ce(OH)2+形式存在的。在稀土离子交换过程中，Ce(OH)2+首先通过物理吸附作用定位在分子筛的超笼中，继而在焙烧过程中脱去水分子由超笼进入到方钠石笼中，适度的离子交换度可提高分子筛的催化活性。且由于稀土离子的引入，在提高重油转化和收率方面有显著改善。在催化裂化过程中，这些指标实际上与原料在催化裂化催化剂中的内扩散也密切相关。对于原料大分子在分子筛中的传质行为与重油转化效率之间也存在一定的关系，目前这方面的研究尚未系统开展，催化剂中大分子传质行为的研究依然亟需深入。运用传统的实验方法去研究大尺寸、复杂分子在稀土改性Y分子筛上的吸附扩散性能，不仅存在成本高、操作复杂、消耗时间更多等缺点，而且又无法观察和确定物质在可以到达的分子筛孔道中的吸附和扩散行为[7-8]。与其相比，利用计算机模拟的方法不但成本更低、安全且不受各种反应过程的限制，准确性和重复性更好，又可以清楚地观察到反应物在分子筛孔道内的运动过程，并考察此过程的热力学性质和动力学性质[9]。蒙特卡洛方法是模拟计算常用的方法，可应用于研究吸附分子在分子筛中的能量与位置以及其随吸附量、温度、压力等的变化。并可以提供吸附等温线，径向分布函数等数据[10]。

本课题以1-辛烯、正辛烷在催化裂化过程中Ce离子改性Y分子筛上的吸附为研究主体，利用巨正则蒙特卡洛(GCMC)的方法和分子动力学(MD)[11-12]方法探究正辛烷、1-辛烯在CeY分子筛上吸附扩散的行为，为实验提供理论支持。

1 计算模型和计算方法

1.1 分子筛模型的建立

利用Accelrys公司的Material Studio 5.5软件数据库建立Y型分子筛骨架结构，其结构参数为：空间群为Fd-3，晶胞参数a=b=c=2.502 8 nm，α=β=γ=90°。建立2×2×2的超胞模型(ultra cell，UC)，利用perl程序将模型中的部分Si原子替换为Al原子，Al原子的分布遵循Lowenstein规则[13]，将分子筛骨架中的硅铝比调整为2.62，此时，分子筛骨架中含Al原子424个。再用Sorption模块向体系中加入相应的Na+和Ce(OH)2+以平衡由于Si被Al取代而产生的负电荷，其中Ce(OH)2+的交换度为45%，由下式得到：

(1)

式中：q为阳离子所带电荷数；m为阳离子个数；x为Ce取代前的NaY中Na+的个数；X为阳离子交换度，%。图1为NaY分子筛及Ce(OH)2+质量分数为45%的CeY 分子筛的结构模型。由式(1)计算可知，在CeY模型中含Ce(OH)2+共96个。

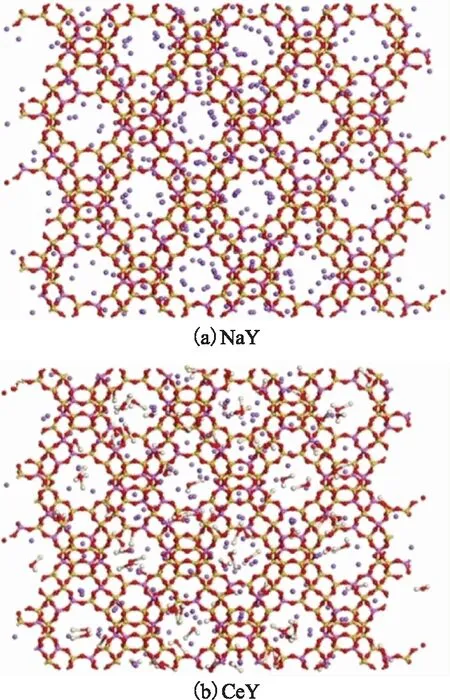
图1 NaY分子筛及Ce(OH)2+质量分数为45%的CeY分子筛的结构模型—H； —O； —Si； —Na； —Al； —Ce

1.2 计算方法

在吸附模拟前，应用DMol3模块，采用BLYP交换相关泛函数和DNP基组对吸附质分子进行基于量子化学的结构优化。在巨正则蒙特卡洛模拟吸附过程中，采用COMPASS力场[14]，该力场基于量子力学从头计算，将有机与无机力场相统一，更能够准确模拟有机物分子与分子筛之间的作用。利用Sorption模块模拟吸附质分子在分子筛中的吸附扩散行为，随机取样方法为Metropolis取样，即在模拟过程中，吸附质分子的出现与消失具有相同的概率，分子筛与吸附质分子以及吸附质分子之间的静电相互作用的处理采用Ewald加和方法，而范德华力的相互作用利用Atom based方法，截断半径为1.85 nm。计算过程中的模拟步数设为1.1×107步，为了使体系平衡，前1×106步设为平衡段，剩下的1×107步设为取样段。

1.3 吸附等温线拟合模型

为了说明Ce(OH)2+对NaY分子筛吸附的影响，对使用GCMC方法得到的吸附等温线数据，分别利用Langmuir和Langmuir-Freundlich两种吸附模型对吸附等温线进行拟合。

Langmuir等温方程在吸附扩散领域应用甚广，其模型假设吸附剂表面均匀，吸附分子间无相互作用，且单分子层吸附，即一个活性位点只能占据一个分子。Langmuir方程拟合式为：

(2)

式中：Q为吸附量；Qm为饱和吸附量；b为吸附平衡常数，即吸附系数，它与温度有关；p为组分的分压。Langmuir-Freundlich等温方程[15]是在结合Langmuir方程与Freundlich方程基础上建立的方程，考虑了吸附位分布不均匀，以及吸附质分子间存在相互作用时表面的吸附。Langmuir-Freundlich方程拟合式为：

(3)

式中，n代表均相指数，n越趋近于1，吸附剂表面的吸附越均匀，吸附质分子间作用力越小且分散越均匀，越符合理想的Langmuir等温吸附方程。

1.4 吸附能量和吸附热

吸附能在吸附过程中是一个重要的参数，它是由体系中所有的吸附质和吸附剂之间以及吸附质与吸附质之间的能量决定的。

Ead=Eads-ads+Eads-zeo

(4)

式中：Ead为体系总能量；Eads-ads为吸附质和吸附质之间的相互作用能量；Eads-zeo为吸附质和分子筛之间的相互作用能量。

在吸附过程中分子放出热量，从而达到相对稳定状态，吸附热计算式如下：

(5)

式中：Q1为吸附热；R=8.314 J(molK)，为气体常数；Ead为Eads-ads与Eads-Zeo之和；Eintra为吸附质分子势能；Nad为吸附质个数[11]。

1.5 吸附能量密度等高截面图

为了能够直观地观察到吸附质在CeY中的吸附情况，选取十二元环中心来进行截面[12]，图2a中蓝线为截取位置，先对模型构建Connoly 表面，然后在对其进行截面。图2b为十二元环结构图，图2c为图2a左视图，图2d为吸附能量密度俯视图，可以清晰地看到十二元环以及其它原子分布情况。

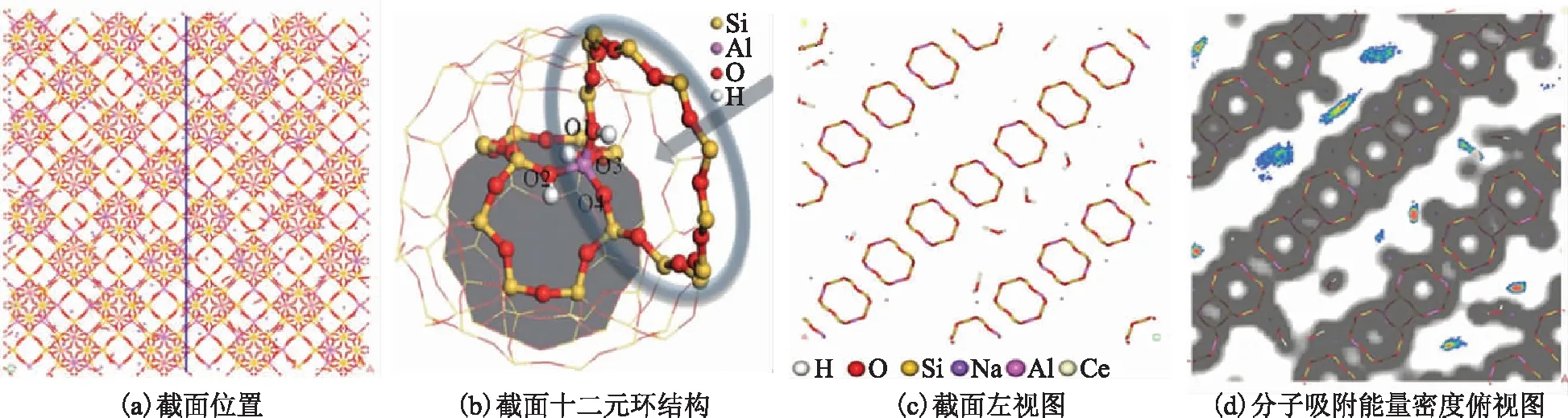
图2 CeY骨架结构及分子吸附能量密度分布—H； —O； —Si； —Na； —Al； —Ce

2 结果与讨论

2.1 吸附等温线

为了探讨正辛烷和1-辛烯在Ce离子改性Y型分子筛上吸附扩散行为，应用GCMC方法分别在303 K、423 K温度下对其进行模拟研究。模拟压力从1.0×10-14kPa到其饱和蒸气压，正辛烷和1-辛烯分子在不同温度下的饱和蒸气压如表1所示。正辛烷和1-辛烯在CeY分子筛上的吸附等温线如图3所示，图中散点为原始模拟数据，线为对原始模拟数据进行的Langmuir-Freundlich模型拟合数据。由图3可知：在温度为303 K时，当压力增加到1×10-7kPa左右，正辛烷和1-辛烯分子开始在CeY上吸附，随后吸附量迅速上升，并在3.2×10-3kPa时吸附逐渐趋于平缓并最终达到吸附饱和；而在423 K时，正辛烷、1-辛烯分子在压力达到2.49×10-3kPa时才开始进行吸附，随后吸附量亦快速增加，并在4.48 kPa压力下逐渐趋于吸附饱和。

表1 正辛烷、1-辛烯在不同温度下的饱和蒸气压 kPa

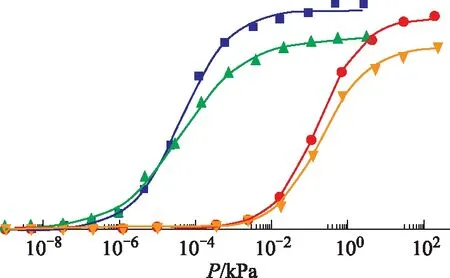
图3 不同温度下正辛烷和1-辛烯在CeY分子筛上的吸附等温线■—303 K-CeY-正辛烷； ▲—303 K-CeY-1-辛烯； ●—423 K-CeY-正辛烷； 辛烯

在303 K温度下，正辛烷和1-辛烯的饱和吸附量都大于423 K下的饱和吸附量。这是因为在低温下，分子动能较低，CeY仅需一个较小的作用力就可以牢牢地将吸附质吸附在活性位点上；而423 K下，分子热运动加剧，分子动能较大，吸附质与分子筛之间的范德华力被削弱，从而使得CeY分子筛无法捕捉到较多的气体分子，导致饱和吸附量的下降；303 K、423 K温度下，正辛烷的饱和吸附量都大于1-辛烯的饱和吸附量。

为了进一步研究正辛烷和1-辛烯的吸附行为，分别用Langmuir以及Langmuir-Freundlich吸附模型对模拟出的吸附等温线进行拟合，拟合数据如表2所示。

根据表2中相关系数(R)的比较可以看出：两种拟合方法的相关性都很高，接近于1；但Langmuir-Freundlich模型对吸附等温线拟合的相关程度比利用Langmuir模型拟合的效果更好，说明正辛烷、1-辛烯的吸附行为，并非单分子层吸附，而且分子筛上吸附位分布并不均一，分子和分子之间存在相互作用力；303 K下，Langmuir-Freundlich模型拟合均相指数(n)较小，1-辛烯吸附的n值小于正辛烷的n值；这是由于Ce(OH)2+的引入造成分子筛吸附位分布不均一，且1-辛烯分子之间的相互作用力更强而导致的；Langmuir-Freundlich模型的饱和吸附量更接近原始数据，相关性更好；随着温度升高，423 K下Langmuir模型R值和Langmuir-Freundlich模型R值都更接近1，Langmuir-Freundlich模型中n值变大，1-辛烯的n值略小于正辛烷的n值，但相比低温二者n值更加接近。这说明温度升高使得气体分子动能增大，在体系中分散度更高，1-辛烯分子间相互作用也减弱。

表2 不同温度下CeY与正辛烷、1-辛烯的Langmuir和Langmuir-Freundlich模型拟合参数

2.2 吸附质与吸附剂之间的相互作用

2.2.1吸附势能曲线为了进一步探讨正辛烷、1-辛烯与CeY之间的相互作用，从吸附能量角度来对其进行考察。图4为不同温度、不同吸附质的吸附势能变化曲线。图5是303 K、423 K温度下两种吸附质在吸附过程中吸附质的分布密度。

图4 不同温度下CeY分子筛与正辛烷和1-辛烯之间的吸附势能曲线

图4a为303 K下不同压力时正辛烷在CeY上吸附势能曲线。由图4a可以看出：在1.56×10-7kPa下，有少量正辛烷分子开始吸附；虽然曲线上看似只有一个峰，但是经过拟合后发现，在-87.94 kJmol处的主峰右侧-82.5 kJmol的位置上有一个伴峰，在压力小于3.25×10-3kPa的情况下都可以看出这2个峰。这说明在开始吸附到压力较小时，正辛烷在CeY上存在两种位置的吸附。由图5a可以看出：在低压吸附时，正辛烷在Ce(OH)2+附近存在吸附密度，当压力逐渐增加后，正辛烷的吸附逐渐转向Na+附近，Ce(OH)2+附近正辛烷出现的概率大大减弱；当吸附压力高于3.25×10-3kPa时，吸附逐渐趋向饱和，势能曲线的变化也趋向稳定，最后在吸附压力达到2.46 kPa时，正辛烷的吸附量达到饱和。此时，由图5a可以看出，正辛烷只和分子筛骨架及Na+发生作用，吸附势能曲线中只有一个势能峰。但是当温度升高至423 K时(如图4c)，无论压力高低，正辛烷在CeY上吸附势能均只有一种，同时，随着吸附压力的升高，峰位出现了明显的位移，最可几相互作用随着吸附压力的增大而变小，这与低温时的变化情况相似。结合图5b可以看出，高温下吸附密度出现的区域都是在Na+附近，这说明正辛烷在Ce(OH)2+附近的吸附虽然比在Na+附近的吸附稳定，但是受吸附温度影响较大，温度升高后，正辛烷在Ce(OH)2+附近的吸附能力变低。

图5 不同温度下CeY分子筛与正辛烷和1-辛烯之间的吸附势能密度截面分布红蓝色块代表正辛烷或1-辛烯的分布概率，红色为出现概率高，蓝色为概率低

对于1-辛烯分子的吸附，其情况与正辛烷稍有不同。结合图4b和图5c可以看出：在低温下，吸附势能曲线存在2个峰，即-87.78 kJmol、-96.14 kJmol，即两种相互作用力，1-辛烯的吸附位同时出现在Na+和Ce(OH)2+附近；随着吸附压力的增加，-87.78 kJmol位置的势能峰依旧存在，但是-96.14 kJmol位置的势能峰则随之迅速降低，直到4.89×10-6kPa饱和吸附压力下几乎消失。说明在压力增大的过程中，随着1-辛烯吸附量的上升，有一种相对较弱的相互作用力逐渐减小甚至消失；当温度较高时，1-辛烯在CeY上的吸附也只有一种吸附势能，且随着吸附量的增加没有较大的变化；与正辛烷吸附进行对比后发现，1-辛烯的吸附势能变化远小于正辛烷。

由以上分析可以看出，303 K下1-辛烯与正辛烷的吸附类似。均是在低的吸附量时才能稳定地出现吸附质分子与Ce(OH)2+的作用。随着吸附量的增加，这种吸附作用逐渐减小。这也可以认为，吸附质分子与CeY作用时，由于Ce(OH)2+的数量是固定的，无论吸附量增加多少，吸附在Ce(OH)2+的分子数量是不会发生变化的，所以大多数的分子都是在Na+附近和骨架旁边吸附。从吸附势能曲线的移动可以看出，正辛烷与CeY之间的相互作用随着吸附压力增加和吸附量的增加影响较大。反之，1-辛烯随着吸附压力增大与吸附量的增加对其相互作用影响较小。由此推断，这可能是由于1-辛烯上的C=C键产生的π-π相互作用，导致1-辛烯分子与CeY之间存在比正辛烷分子与CeY间更强的相互作用而导致的。正辛烷、1-辛烯与CeY之间的主要相互作用在孔道中的Na+附近。

根据饱和吸附压力下的势能分布曲线，整理出不同温度下正辛烷、1-辛烯与CeY分子筛之间最可几相互作用能量，如表3所示。

表3 正辛烷、1-辛烯在CeY分子筛中饱和吸附时的最可几相互作用能 kJmol

表3 正辛烷、1-辛烯在CeY分子筛中饱和吸附时的最可几相互作用能 kJmol

温度/KCeY-正辛烷CeY-1-辛烯303-88.67-86.87423-84.18-83.54

由表3也可以看出，423 K下正辛烷、1-辛烯的最可几相互作用能都大于303 K下的最可几相互作用能。这是由于温度的升高，分子动能增加，从而提高了体系的能量，使吸附态趋向较不稳定的情况，从而降低了CeY与吸附质之间的结合能，导致饱和吸附量的降低。且不论是高温、低温下，1-辛烯的最可几相互作用能也都大于正辛烷，所以在不同温度下，正辛烷的饱和吸附量要大于1-辛烯，也印证了吸附等温线的结果。

为了直观地观察正辛烷、1-辛烯在CeY上的扩散情况，探究了在不同温度下饱和吸附情况下的单元晶胞上吸附质的势能密度分布情况，如图6所示。

图6 不同温度下正辛烷与1-辛烯在CeY分子筛上的势能密度分布蓝色越深说明分子势能越高，红色越深则说明分子势能越低

从图6可以看出：在303 K下(图6a、c)正辛烷和1-辛烯的分布范围较为集中；在423 K下(图6b、d)吸附质分子的分布范围更大。这是由于温度的升高，分子动能增大，从而增大了分布范围。从不同吸附质来看，不论是低温还是高温，1-辛烯的饱和吸附量都明显低于正辛烷，且1-辛烯的分布更为均匀。对比图6a、b和图6c、d可以看出，正辛烷的分布范围随温度的变化相比较于1-辛烯的变化更大，分布更广。结合表3的数据也可以看出，正辛烷的最可几相互作用能随温度变化较大。

2.2.2吸附热图7为模拟得到的两种吸附质分子在CeY中吸附的吸附热随吸附量的变化曲线。由图7可以看出：正辛烷与1-辛烯在423 K下的吸附热都高于303 K下的吸附热，因为吸附过程是放热过程，在高温下分子动能更大，想要吸附在分子筛上则需要放出更多的能量来降低自身势能从而达到一个相对稳定的吸附态；两个温度下，正辛烷的吸附热都大于1-辛烯，这是由于1-辛烯内部存在C=C键，分子本身的势能高于正辛烷。

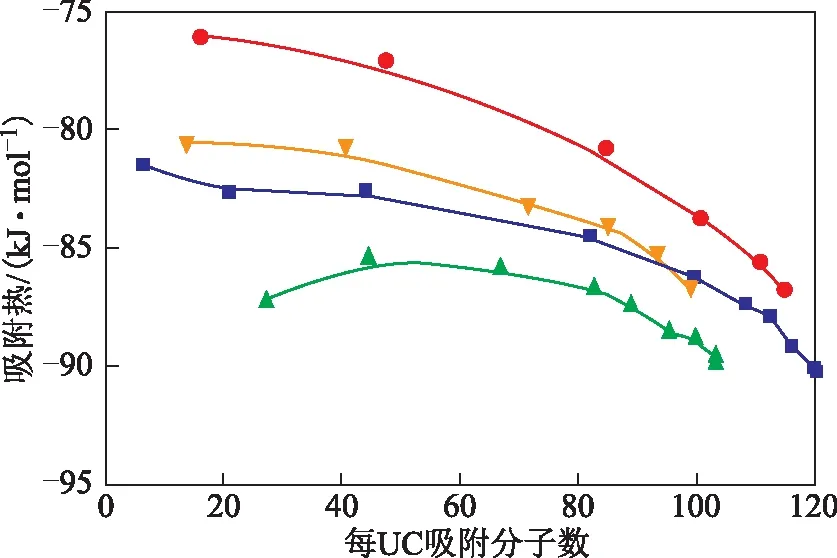
图7 CeY分子筛与正辛烷和1-辛烯之间的吸附热■—303 K-CeY-正辛烷； 辛烯；●—423 K-CeY-正辛烷； ▲—423 K-CeY-1-辛烯

从图7还可以看出：正辛烷、1-辛烯的吸附热，在吸附量较小的情况下变化较为缓慢，在吸附量增大时，吸附热降低的速率也更快。这说明吸附量的大小对于吸附热有一定的影响；随着吸附量的增大，分子和分子之间相互作用也越来越明显，分子与Ce(OH)2+之间的相互作用会减弱，新来的气体分子只要释放相对较少的能量就能吸附在CeY的活性位上；在303 K、423 K下的起始吸附阶段，吸附量较小时，正是由于1-辛烯的吸附热小于正辛烷，所以在起始吸附阶段，1-辛烯先于正辛烷吸附在CeY上；而在吸附接近饱和时，正辛烷的吸附热反而略低于1-辛烯，这也从吸附热角度解释了为什么正辛烷在不同温度下的饱和吸附量会高于1-辛烯；且在吸附起始到饱和正辛烷的吸附热变化幅度大于1-辛烯，也印证了图3中正辛烷能量曲线变化幅度大于1-辛烯的结果。

3 结 论

(1)正辛烷、1-辛烯与CeY分子筛之间的吸附符合Langmuir-Freundlich吸附模型。Ce(OH)2+的引入使得分子筛上吸附活性位分布不均匀，且1-辛烯分子间由于C=C键的存在使其分子间相互作用力更强，因此，在303 K和423 K下，1-辛烯的饱和吸附量均低于正辛烷。

(2)正辛烷、1-辛烯在CeY分子筛上的吸附量对吸附热存在影响，随着吸附量的增加，这种影响也增大。吸附作用中最主要的相互作用力为范德华力，吸附质分子主要与孔道中Na+作用，与Ce(OH)2+之间的相互作用次之，且随着吸附量的增加，分子与Ce(OH)2+之间的相互作用会减弱。