考虑轴承支撑刚度和齿轮轴变形的内啮合齿廓修形研究*

，，

(1.湘潭江麓技工学校，湖南湘潭411105；2.湘潭大学，湖南湘潭411105)

0 引言

齿轮传动是最具代表性的传动机构，虽然其发展历史较长，但在齿轮修形上，很多是根据经验进行的，对修形位置和修形量的精准计算需要进一步开展研究[1]。之前的理论和实践分析表明，适当的齿轮齿廓修形能人为地补偿齿轮啮合时轮齿弹性变形，抵消由于弹性变形产生的干涉，减少齿轮啮入和啮出冲击，达到减震降噪的效果[2-5]。当前国内外主要采用经验公式确定修形量，当采用经验公式修形时，虽方法简单，但由于考虑的因素单一，获得的修形效果不好。有多种因素影响齿轮的啮合，其中齿轮轴的轴承支撑刚度和弹性变形是影响齿轮啮合的重要因素，计算齿轮的修形量时，需考虑以上两因素。在分析原有修形方法的基础上，考虑轴承刚度和弹性变形的影响，推导齿廓修形量计算公式和确定修形曲线[5]。

1 内齿轮当量齿形推导

在计算轮齿弹性变形时，目前应用较多的方法是石川修形公式，其中需用到当量齿形[6]，查阅众多参考文献以及资料，只有外齿轮当量齿形的计算方法，没有关于内齿轮当量齿形的计算公式[5]，开展的研究对象为内外齿轮啮合，故需对内齿轮当量齿形进行推导。

1.1 内齿轮当量齿顶厚Sk和当量齿高h

分析图1所示的内齿轮几何关系可知，当量齿顶厚为：

Sk=2rasinφ

(1)

式中，ra为齿顶圆半径，φ为展开角。

内齿轮渐开线在齿顶处的展开角小于标准压力角，因此有：

(2)

式中，αa为齿顶处渐开线压力角，s为分度圆齿厚，r为分度圆半径，α为标准压力角。将(2)式代入(1)式得：

(3)

由图1所示几何关系，内齿轮当量齿高为：

(4)

式中，rf为齿根圆直径。

1.2 啮合接触载荷点高度hx

如图2所示，可得：

(5)

式中，αx为瞬时啮合接触点处压力角，μ为某时刻啮合接触处载荷作用角。

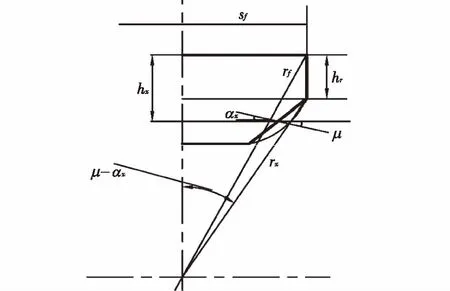
图2 内齿轮当量齿形载荷作用点确定示意图

1.3 载荷作用角μ

如图3所示，可得：

αx+μ=φ

(6)

(7)

将式(7)代入式(6)得：

(8)

图3 内齿轮当量齿形载荷作用角示意图

1.4 矩形部分高度hr和齿根厚Sf

对于内齿轮，不仅齿根圆半径大于基圆半径，有效齿根圆半径也大于基圆半径，当量齿形的梯形与矩形的交点为有效齿根圆与齿廓交点，根据图2可得：

(9)

(10)

式中，rf为齿根圆半径，αf为齿根圆处压力角。

2 啮合点位置变化的分析

图4 支承轴承变形与轴变形的 叠加的示意图

在计算齿轮轮齿的弹性变形时，往往认为轴和轴承为刚性体，忽略这部分弹性变形对轮齿变形的影响。但实际上轴和轴承都为弹性体，两者会同时发生弹性变形，如图4所示。

当承受径向载荷，先假设支撑齿轮轴的轴承是刚性而轴是弹性，齿轮轴的挠曲角为θ1，挠度值为w1；然后假设轴承具有弹性而轴是刚性时，齿轮轴的挠曲角为θ2，挠度值为w2。两种情况下挠曲角相加，为轴系总的挠曲角；两种情况下挠度相加，为轴系总的挠度，即：

θ=θ1+θ2

(11)

w=w1+w2

(12)

齿轮轴发生弹性变形时轴端的挠度值为w1和挠曲角θ1，可以根据材料力学方法求得。由于轴承弹性位移引起的轴端径向位移量w2和挠曲角θ2与轴承刚度有关，如图4(c)所示，假设A、B处轴承刚度分别为K1、K2，则由支撑变形引起的轴端径向位移量w2和挠曲角θ2分别为：

(13)

(14)

支撑刚度的计算方法很多，刘显军、洪军等人[7]采用有限元迭代法进行求解，该方法考虑了预紧载荷的影响，通过迭代能够很好的保证求解精度，现采用两位学者的方法来计算轴承的支撑刚度。

支撑轴承和轴的变形导致传动齿轮倾斜，从而改变两啮合齿轮啮合点的位置，使啮合接触线偏移或转动，如图5。从单个齿轮看，虽然轮齿上的实际啮合接触线相对于理论啮合接触线发生了偏离，但仍然认为实际啮合接触线为一条直线，并与理论啮合接触线的夹角为θ，该夹角是两啮合齿轮因受载使齿轮轴倾斜，两齿轮轴之间的夹角，理想情况下为0。

图5 齿根圆实际半径与理论半径

根据轴的挠度值，沿直径大的方向，啮合接触线移动的距离为w，将两啮合齿轮啮合点投影在轴上，分别计算两轴在投影点处的挠度值，w等于挠度值之和。当然，对于内啮合齿轮，内齿轮的支撑可认为是刚性支撑，只考虑外齿轮轴的倾斜。考虑实际啮合接触线倾斜于理想啮合接触线，使得载荷作用点偏移，从而使齿根圆有效半径和轮齿接触齿宽都发生了改变，如果要采用石川修形公式求齿轮修形曲线时，应对参数进行如下修改。

(15)

(16)

b′=b*cosθ

(17)

3 齿廓最大修形量计算

根据直齿轮的啮合综合刚度理论，齿轮在啮合过程中，啮入和啮出时刻的综合啮合刚度最小，从而齿轮轮齿的综合弹性变形量为最大。

齿轮由单齿啮合进入双齿啮合或双齿啮合进入单齿啮合时，轮齿会产生一个沿啮合线方向上的弹性位移δs[8]，如图6所示。啮入时弹性变形最大，计算此刻的弹性变形量，即可作为齿廓的最大修形量，齿轮的修形就是从理论上补偿这一弹性变形δs，从而减小齿轮啮入和啮出时的冲击[9]。

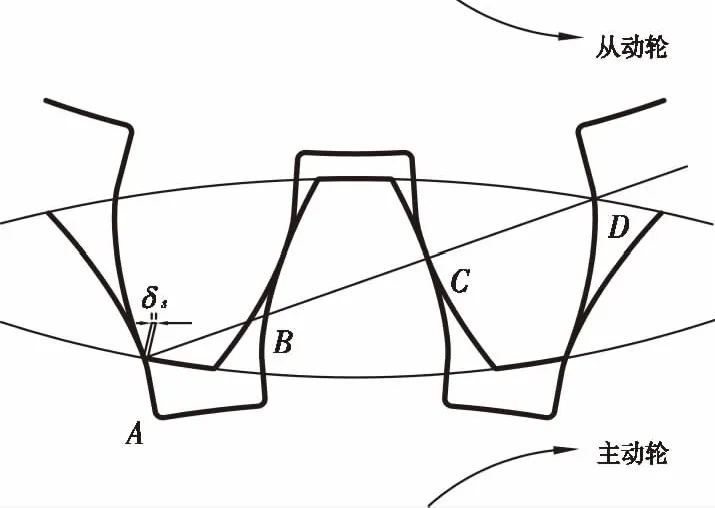
图6 齿轮啮入时弹性变形

根据石川修形公式，齿轮副在载荷作用下发生的弹性变形为[8]：

(18)

式中：δbr为当量齿形长方形部分的弯曲变形量，δs为由剪力产生的变形量，δbt为当量齿形梯形部分的变形量，δg为基础部分倾斜产生的变形量，δp为齿面接触变形量。

由于是计算啮入时刻齿轮轮齿的弹性变形，所以，外齿轮齿顶处为载荷作用起点，而内齿轮的有效齿根圆处为载荷作用起点，由于齿轮在加工中难免存在误差，故齿廓最大修形量为：

Δmax=δ∑+δi

(19)

式中：δi为由于制造误差的原因，所引起的齿轮在啮入啮出时产生的干涉量，由下式获得：

δi=cosαfpt

(20)

式中：α为齿轮标准压力角，fpt为齿轮的周节极限偏差。

4 修形曲线的确定

齿廓上修形部分的修形量和位置通过齿廓修形曲线来表达[10]，即使采用相等的最大修形量，但如果修形曲线不同，对提高齿轮啮合性能的影响也不一样，为获得最好的修形效果，确定科学的修形曲线也非常关键。齿廓的修形曲线公式为[9]：

(21)

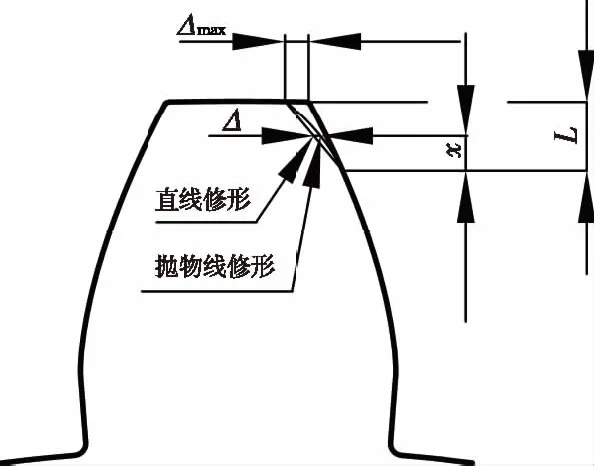
图7 齿廓修形示意图

式中：Δ为齿轮在某一啮合位置上的修形量；L为齿轮修形长度；Δmax为齿廓最大修形量；x为两齿轮啮合位置相对于单双齿啮合切换点处的坐标；b为幂指数，当b=1时，齿廓的修形曲线变为直线，b=2时，齿廓的修形曲线为抛物线，实际中经常采用这两种修形曲线对齿轮进行修形，如图7。

朱传敏等[11]试验证明，如果齿轮传动在轻载低速的情况，修形曲线对齿轮的啮合性能影响效果不大，但在高速和重载的情况下，对齿廓进行抛物线修形，能显著改善齿轮的传动性能，并且优于其他曲线的修形。

5 齿廓修形长度的确定

按修形起始点的位置不同，齿廓的修形长度分为长修形和短修形两种[9-10，12]。如图8所示，沿着啮合线，长修形为啮合的上下界点到双齿啮合的起始点或者终结点处[9]，如图中B2D或者B1C。

图8 修形长度示意图

长修形长度L可由式(22)计算：

(22)

式中：Z为啮合线长度，pb为端面基节。

采用长修形，齿廓修形曲线将更加平滑，齿轮在高速重载情况下，多采用长修形。本文所研究的变桨输出齿轮啮合为重载情况，拟齿轮采用长修形。

6 齿廓修形量计算程序开发

由于石川修形公式比较复杂，如果想通过这种理论计算的方法得到齿廓修形量，那将是一件非常繁琐且易出错的工作。基于Visual C++平台，开发计算程序。通过该程序，只要在程序界面上输入齿轮的基本参数，便可通过修正了的石川修形公式，计算出齿廓最大修形量，所开发程序界面如图9所示。由于齿轮支承和轴结构尺寸变化大，使用该修形软件时，应参考前面所提方法，先计算轴的挠度和挠曲角，在齿轮轴变形参数框中输入，该软件便自动计算出最大修形量。

图9 所开发的齿廓修形量计算程序界面

7 齿廓修形设计应用举例

XE93变桨减速器输出轴齿轮及其配对内齿轮的模数m=14，齿数z1=14、z2=117，变位系数x1=0.5=x2，齿轮使用材料20CrMnTi。将这些参数输入到程序，并将计算得到的小齿轮轴的挠度0.073和挠曲角0.00013输入，得到这对齿轮啮入时刻齿廓的综合弹性变形量如图9所示，为1.064 mm。按照6级精度考虑制造齿轮，误差带入的修形干涉量为0.024，从而得到齿廓最大修形量为：

Δmax=δs+δi=1.088 mm

(23)

当修形量确定后，考虑减速器的工况，采用抛物线修形和长修形方式。

在SolidWorks中，根据修形曲线对齿轮副建模，首先在工程分析软件(Abaqus)进行有限元分析，得到修形前后齿轮副在啮入时刻的应力云图如图10所示；然后在动力学分析软件(Adams)中进行动力学分析，得到内齿轮转速如图11。

图10 修形前后齿轮应力云图对比

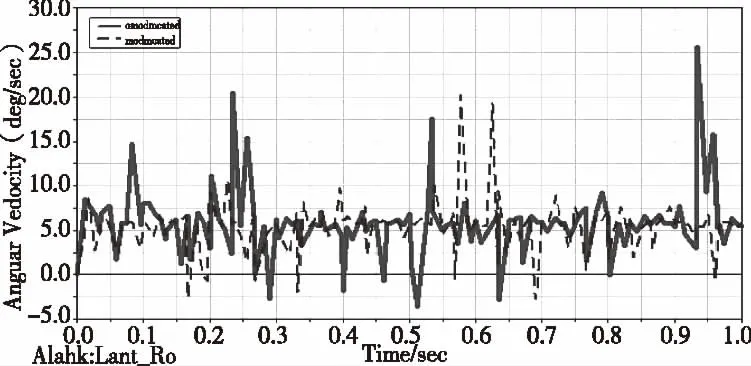
图11 内齿轮转速随时间变化关系

通过图10可以发现，当齿轮没有修形，齿轮啮入时，在齿廓两侧出现了应力集中现象；齿轮修形后，仅单侧出现应力集中现象，并且应力值成倍下降。可见通过齿廓修形，改善了齿轮啮入啮出时载荷冲击，减少应力集中。

图11中实线表示内齿轮没有修形时转速波动情况；虚线表示内齿轮进行齿廓修形后内齿轮转速的波动情况。从图可以看出，对齿轮修形后，转速比没有修形时要平稳，从而显著降振动和噪音。所以从数值仿真分析结果来看，齿廓修形改善了齿轮传动效果。

在变桨减速器投入批量生产之前，为验证其可靠性与稳定性，需对其进行性能试验，试验台原理如图12。

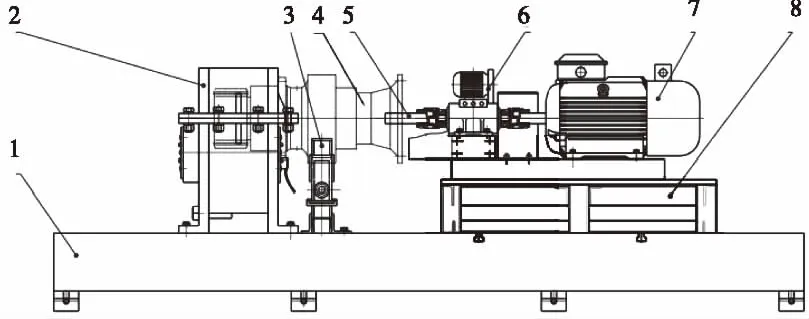
1-试验台底座；2-对扭传动箱；3-支架；4-被试件； 5-驱动轴；6-转矩转速传感器；7-电机；8-可调支架。 图12 减速器性能测试试验台的结构示意图

按照原理图搭建的试验台如图13，采用两个变桨减速器同时开展试验，一为被试件，另一个为陪试件。两个电机，一为驱动电机，一为负载电机，两个电机对扭，两电机采用两个变频器控制，负载电机通过变频器，功率回馈到电网，从而使试验台的能耗很低。在电机和减速器之间都装有转矩和转速传感器，通过这两个传感器可得到驱动功率和负载功率，从而可计算变桨减速器的传动效率。在变桨加速器的相应位置布置振动传感器和温度传感器等，通过采集到的数据对减速器的传动性能进行评定。

图13 减速器性能试验台

在试验台上，按额定转速和额定载荷对变桨减速器进行了200小时试验，试验结束后，取下齿轮输出轴，洗去油污后，对齿面进行仔细观察，发现齿轮的磨损非常少，没发现明显的边缘接触现象，看不到任何点蚀。测量了齿轮的公法线长度，与原检测前几乎没有变化。证明通过修正后的石川修形公式所得到的修形量和修形曲线是可靠的。

8 结论

1)为对内齿轮啮合的齿轮副进行齿廓修形，必须首先计算其当量齿形。

2)考虑了齿轮轴轴承支撑刚度和齿轮轴弹性变形对齿轮轮齿弹性变形的影响，正确的修正了石川修形公式中三个重要参数。

3)通过编程计算得到了齿廓修形量，并以抛物线长修形为其修形方式。通过ABAQUS和ADMAS的数值仿真分析表明，修形齿轮有明显优于未修形齿轮的传动性能。