Φ73水力振荡器振动建模以及碟形弹簧优化设计
, ,
(长江大学机械工程学院,湖北荆州434023)
0 引言
在水平井钻探中,由吴欣袁[1]等人的研究可知,振动传播的距离与振动的幅度成正比,因此使水力振荡器系统的固有频率与振荡元件的激励频率相同时,使之共振,能大幅增加水力振荡器系统的振幅,达到振动传播距离最大的目的,这样对解决托压问题十分有利。
而在水力振荡器系统中,常采用非标准的组合碟簧组,将液体的能量转化为碟簧的势能,带动水力振荡器的振动节进行振动[1-6]。碟簧设计的质量直接影响到水力振荡器系统的工作性能。因此,碟簧结构参数的优化设计便显得非常重要。
1 Φ73水力振荡器系统分析
1.1 结构
Φ73水力振荡器的结构示意图如图1所示,由上部的振动短节和下部的水力振荡短节组成,主要零件有芯轴、碟簧组、射流元件、活塞、缸体、活塞杆以及直旋作动器。
1.2 工作原理
钻井液经过轴向振动短节的芯轴中心通孔进入水力振荡短节,通过射流元件喷嘴后形成高速射流,在射流元件内部进行附壁切换,驱动下部活塞在缸体内做往复运动。同时,与活塞杆下端相连的直旋作动器使节流孔上方旋转套做往复旋转运动,周期性地改变节流口的过流断面面积,使得振荡短节入口处产生周期性的脉冲压力波。当压力升高时,流体压力作用水力振动节系统,迫使芯轴压缩碟簧组向左运动,芯轴伸出。当压力降低时,已压缩的碟簧组释放能量,推动芯轴向右运动。这样下部的振荡短节为上部的轴向振动短节提供了动力,从而驱动连续油管往复运动,在滑动钻进中解决托压问题。
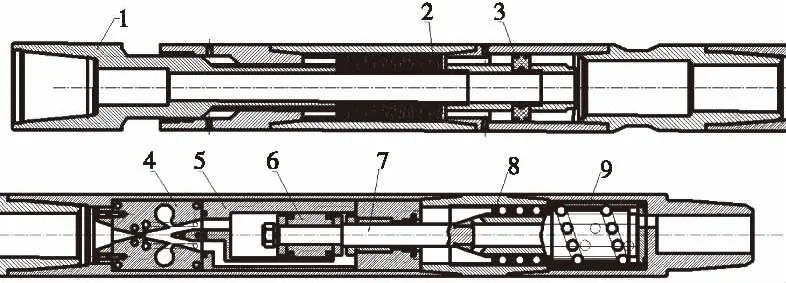
1-芯轴;2-碟簧组;3-斯特封活塞;4-射流元件;5-缸体;6-活塞;7-活塞杆;8-直旋作动器;9-旋转套。 图1 Φ73水力振荡器结构示意图
2 Φ73水力振荡器系统振动力学模型的建立
2.1 振动力学模型
在振动短节中,振动所需的激振力由振荡短节提供,振动短节内碟簧组的运动带动芯轴进行运动,从而产生振动。该水力振荡器系统的振动为有阻尼的受迫振动,其振动微分方程为:
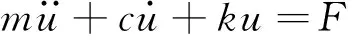

再令:
得到:
系统的稳态响应:
u=bsin(ωt-ε)
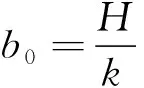
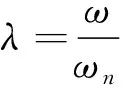
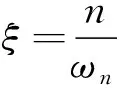
在一般情况下,阻尼比ξ<<1时,可以认为共振频率ω=ωn,即激振力频率等于系统固有频率,系统发生共振,共振振幅为:
2.2 系统固有频率
用能量法计算水力振荡器系统的固有频率,工程中不考虑系统的阻尼,则该系统为保守系统[7]。计算该系统的最大动能Tmax和最大势能Vmax,由机械能守恒定律,有:
Tmax=Vmax
再算出系统的固有圆频率:
即系统的固有频率为:
其中:k为组合碟簧的总刚度,N/mm;m为碟簧—芯轴系统的总质量,kg。
3 碟簧的设计
3.1 设计方法的介绍
为了实现共振的目的,往往需要对Φ73水力振荡器系统中的非标准碟簧组进行单独设计。然而现阶段,非标准碟簧的设计方法往往只有两种,一种常规设计,另一种计算机优化设计。前一种方法需要在设计过程中多次尝试,需要耗费大量精力。
3.2 常规方法的设计处理过程
首先选定碟簧的特性曲线。其次根据碟簧空间限制,选定碟簧外圆直径D与内圆直径d并确定比值C,如图2所示。再给定f/h0的值,并由应力计算公式计算出满足强度要求的碟簧厚度t。最后依据载荷与变形的关系,确定碟簧组合方式和片数,组合碟簧采用叠合再对合的方式,叠合层数为n,对合次数为i,如图3,再将组合碟簧以并联的方式安装在芯轴上,并联个数为num。
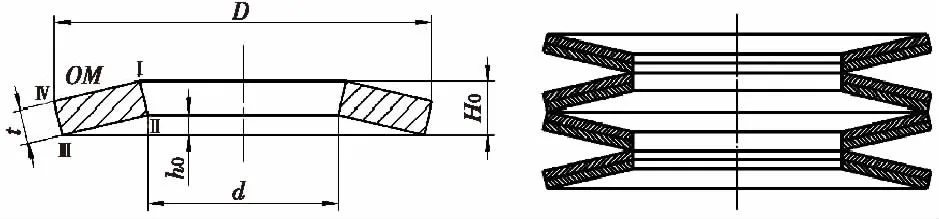
图2 单片蝶形弹簧图 图3 复合碟形弹簧图
3.2.1 确定已知参数
如图1,单个碟簧的结构主要由4个尺寸参数决定(h0,t,D和d)[8-10],由于结构的限制试取D=58 mm,d=34.5 mm,系统固有频率与激励频率相同(10 Hz ~20 Hz)。
3.2.2 常规计算结果
当h0/t=0~0.5时,弹簧特性曲线接近直线,与圆柱压缩螺旋弹簧近似。取:
内外径比值:
应力公式系数的值:
碟簧无支承面:
K4=1
碟簧压缩极限:
后面的计算中均以下式代入:
最大切应力位于碟簧内圆外表面的Ⅰ处(图2):
≤|σs|
σs=1666 MPa,tmax=2.5 mm
已知芯轴的质量(材料为40CrMnMo):
m1=4.385 kg
内套筒的质量(材料为40Cr):
m2=num[((d+5)2-d2)π·4·ρ+(d2-142)π·ρ(n·t+h0)·i]
碟簧的质量(材料为60Si2CrVA):
m3=(D2-d2)π·t·ρ·i·n·num
m=m1+m2+m3
组合碟簧的总刚度:
经过多次试凑,得到一组结果,叠合层数为3,对合次数为2,并联个数为5,满足条件。
3.3 优化设计计算
由前面计算可知,未知参数为碟簧结构参数h0,t,D和d,叠合层数n,对合片数i,并联个数为num以及固有频率fn,所以设计变量取[11-12]:
x=[h0,t,D,d,n,i,num,fn]
=[x1,x2,x3,x4,x5,x6,x7,x8]
3.3.1 目标函数的确定
为了满足大的振动幅度要求,将组合碟簧的最大压缩量设为目标函数:
maxF(x)=i·fmax
3.3.2 约束条件
1)特性曲线的要求
2)碟簧界限要求
3)碟簧强度要求,碟簧内圆外表面的Ⅰ处的应力应小于材料的屈服极限
|σ1|≤|σs|
4)碟簧空间尺寸要求
52 mm≤D≤56 mm
32.5 mm≤d≤36.5 mm
num≤6
5)碟簧—芯轴系统的频率要求,设计要求为10 Hz ~20 Hz(与振荡节中激振频率相同)。
4 优化结果及对比
4.1 Matlab计算结果
x=[1.215,2.430,56.000,32.500,4.000,5.956,6.000,10.000]
f=-5.427
exitflag =1
4.2 结果对比
从表1列出的结果对比来看,优化设计的最大压缩量明显高于常规计算,更加符合预先的设计目标,并且更为简便,免去了多次试算以及多次调整。优化后的最大压缩量近似为常规计算的多倍,参照吴欣袁等推导出的钻井过程中激励传播距离公式:
式中:LP为振动传播距离;Fa为轴向激励的振幅;μ为动摩擦因数;ρAg为单位长度管柱在钻井液中的重力。
可以预见到,优化后的水力振荡器在钻进过程中振动传播的距离可以显著增加。
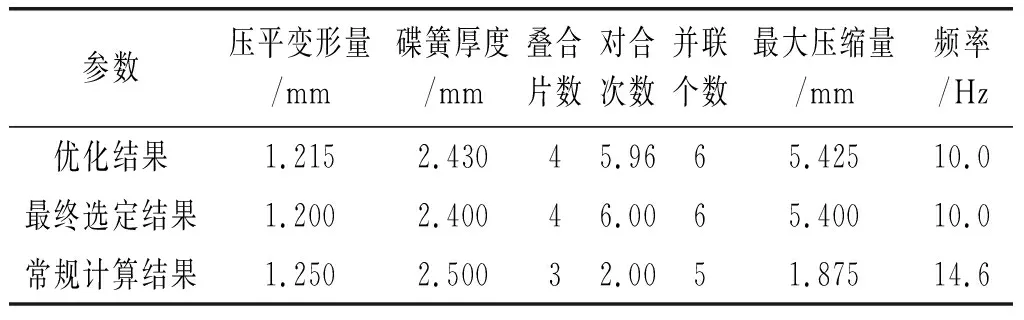
表1蝶形弹簧优化结果与常规结果对比表
根据优化结果最终设计出振动节结构如图4。

图4 振动节结构图
5 结束语
在水力振荡器的设计中,由于碟簧的设计对其性能的影响十分巨大,采用常规方法不仅费时费力,有时候也得不到满意的结果,而利用MATLAB优化计算的方式来设计碟簧不仅能够得到预期的结果,而且比常规方法更加方便和有效。文章还建立了水力振荡器系统振动模型,反映出了该系统振动规律,当系统发生共振时,水力振荡器的振幅显著提高。在以往的水力振荡器设计中大多数都避免出现共振,而笔者则创新性地利用共振的特点来解决托压问题,共振使得水力振荡器的振幅大大增加,同时使得振动在井眼中的传播距离变得更远,这就让管柱在钻进过程中更多的部分由静摩擦变为动摩擦,更不容易发生托压。以上这些为以后研究水力振荡器的振动以及全井钻柱振动提供了有力帮助,对解决托压问题十分有利。

