基于ADAMS的单梁吊具吊索受力不均问题研究分析

，，

(北京航天发射技术研究所，北京100076)

0 引言

单梁四吊索起吊作为一种常用的水平吊装方式，广泛应用于各型号航天产品的吊装转载任务。根据单梁四吊点吊具结构特点，四点承载受力属于超静定问题。由于零部件长度尺寸偏差、被吊产品质心偏差等客观因素影响，必然存在起吊过程中各吊点受力不均的情况。此外，由于部分吊具零部件连接自由度设计不合理、吊索种类选取不合理等原因存在，单梁四吊索吊具的受力不均匀性将更加明显。在某些极限情况下，可能会出现只有两个吊点承载的情况。本文通过问题分析、仿真计算分析等手段，分析单梁四吊索吊具吊点受力不均的影响因素及由此导致的不均匀程度，为后续单梁四吊索吊具的设计提供参考[1]。

1 吊具方案简介及工作原理

1.1 方案简介

本文以某型号四吊索吊具为研究对象，该吊具采用单钩起吊，为框架式结构，主要由吊耳、吊梁、连接叉、止动销、前吊带、后吊带、前连接板和花兰螺栓等组成。吊具组成结构见图1。

图1 四吊索吊具结构组成图

1.2 工作原理

该吊具采用单钩四吊索水平起吊，通过吊耳与吊钩连接，通过前连接板与被吊产品的前端吊点相连，通过花兰螺栓与被吊产品的后端吊点相连。该吊具沿纵向为非对称结构。该吊具通过调节花兰螺栓的长度调节被吊产品与水平面的夹角，保证被吊产品与水平面的夹角不超过3°，且前高后低。不同吊装工况下，后吊带长度和吊带在吊梁上的连接位置均不同。

2 动力学计算模型及边界条件

2.1 计算模型介绍

图2 吊具计算模型

计算模型吊具的整体尺寸、质量质心位置等参数模拟该四吊索吊具进行建模，其中斜拉吊带(共四根)型号为R01-10，额定载荷10 t。前吊索长度2.595 m，后吊索长度3.555 m；被吊产品质量15 t，质心沿被吊产品轴向最大偏差100 mm，横向最大偏差10 mm；计算模型中忽略吊具重量。该四吊索吊具等效计算模型见图2。

该四吊索吊具在计算时对吊具及被吊产品进行如下简化[2-4]：

1)吊具上端吊梁通过吊环与吊车的吊钩连接，在吊环上端中心设置一个MARKER点(MARKER点与大地固定连接)， 在吊梁与MARKER点之间建立一个球铰副，模拟吊具与吊钩的连接，且可绕吊钩在空间内适应性转动；

2)吊梁两侧通过叉架、吊带、连接叉与被吊产品连接，在模型中省略叉架、连接叉等结构件，在吊梁与被吊产品对应连接点之间建立弹簧元件，通过弹簧元件对吊带进行模拟；

3)对被吊产品模型进行简化，省略被吊产品上的起吊组件，通过设置密度值模拟被吊产品实际重量，通过改变被吊产品质心的MARKER点在计算模型中的坐标位置模拟其质心的偏差量。

2.2 四吊点受力不均匀性影响因素

根据吊具结构特点，四点受力不均匀的影响因素主要包含吊带长度差、吊带伸长率、被吊产品质心偏差、吊点位置分布等影响因素。

上述影响因素的存在将导致起吊过程中四吊点受力不均现象，以下通过使用弹簧对吊带进行模拟计算，通过动力学分析对各影响因素进行总结分析，并与以往计算结果进行对比。根据吊具结构特点，对三个影响吊索承载不均匀性的主要因素设置供参考的计算输入，具体如表1所示。以下通过吊具的动力学分析对各影响因素进行分析和总结[5]。

表1主要影响因素的设计输入值

3 吊具动力学计算情况

图3 弹簧位置分布示意图

以吊具动力学模型为基础，对各影响因素进行分析计算，并对计算结果进行分析总结，首先对其中一根吊带偏长的情况进行计算，弹簧位置分布见图3，图示位置为俯视位置，对前左弹簧比其他弹簧偏差0.02 m、0.04 m的情况进行计算，其中被吊产品质心位置理论质心(无偏差)[6-7]。

3.1 单根吊索长度差的影响

理想状态下前后两组吊带的受力应相等，受力结果见图4，吊带长度差情况下吊带受力将存在偏差，其中前左吊带偏长0.02 m时的计算结果见图5。

通过对维生素B1缺乏症的治疗以及预防，减少了动物的死亡率，节约了养殖成本，降低了因维生素B1缺乏引起的各种神经及心血管症状，能直接提供动物所需的硫胺素，从而达到预防和治疗的目的。

图4 理想状态受力计算结果

图5 前左吊带偏长0.02mm受力计算结果示意

如表1所示，在ADAMS模型中，用弹簧代表吊带进行吊具动力学仿真计算。因为吊带的实际伸缩率远小于弹簧，所以在设置弹簧刚度时，需要将弹簧的刚度设置成100000 N/m(该刚度值与实际吊带的伸长率相似)。同时考虑到吊具的不均匀承载是静力学过程，对吊具进行动力学计算时采用静力学计算方法，所以在图4和图5中各吊带的受力曲线是一条直线。

3.2 吊索伸长率的影响

对前左吊带偏长0.02 m、0.04 m的情况分别进行计算，吊带的伸长率分别取值5E5 N/m、1E6 N/m、2E6 N/m、5E6 N/m、1E7 N/m。计算结果对比情况见图6-图8。

图6 前左吊带偏长0.02m时各点受力随伸长率 变化对比

图7 前左吊带偏长0.04m时各点受力随伸长率 变化对比

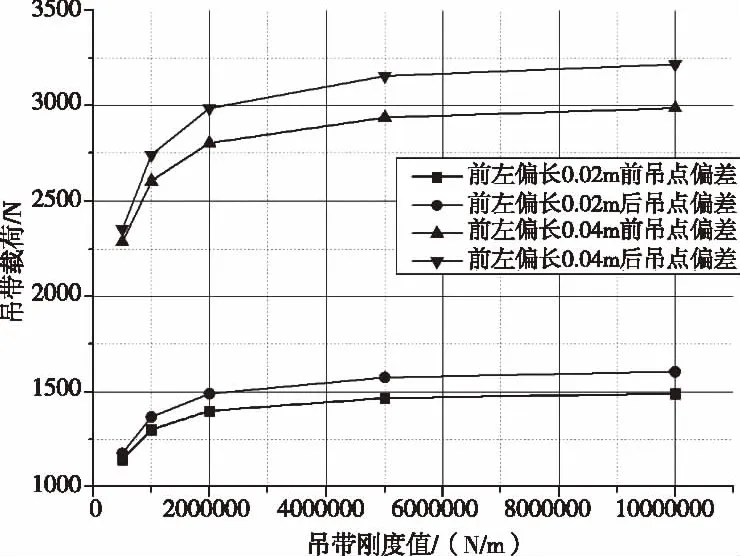
图8 SPRING1偏长两种工况受力偏差对比

通过对上述计算结果进行分析可得出以下结论：

1)吊带长度存在偏差时，各点受力存在不均匀性，受力不均匀程度与吊带长度差数值成正比，长度差越大各点受力偏差也越大；

2)在特定偏差情况下，各点受力的不均匀性也受吊带伸长率影响，伸长率越大时各点受力偏差也越大；

3)该吊具结构形式受吊带长度和伸长率影响均偏小，当伸长率由5E5 N/m增大至1E7 N/m时，吊点最大受力偏差1000 N；当长度差变化时，各点受力偏差最大1500 N。根据上述偏差计算吊点不均匀系数最大为1.03。

以上计算对吊具四吊点吊带的长度和伸长率影响情况进行了分析，后文继续对被吊产品质心偏差情况进行分析，进一步总结四吊点斜拉起吊的恶劣工况及各吊点受力的不均匀程度。

3.3 被吊产品质心偏差的影响

对被吊产品质心偏差进行计算，以模型俯视图中自左向右为X轴正向，自下向上为Y轴正向，根据总体任务书要求：质心X轴方向最大偏差量为100 mm，Y轴方向最大偏差量为10 mm，以前左吊带偏长0.04 m为例，对质心偏差(+0.1 m、+0.01 m)、(-0.1 m、+0.01 m)进行分析，上述偏差位置比其他质心偏差位置对受力的不均匀性影响最大。上述计算对应的计算结果见图9-图11。

图9 前左吊带偏长0.04m、质心偏差(+0.1、+0.01) 计算结果

图10 前左吊带偏长0.04m、质心偏差(-0.1、+0.01) 计算结果

通过对上述计算结果进行分析可得出以下结论：

2)被吊产品的质心偏差位置的影响因素较小，两种位置引起的偏差量不大于500 N，对吊具受力计算可忽略不计；

图11 前左吊带偏长0.04m、两种质心偏差载荷对比

3)考虑质心偏差影响时吊点受力最大偏差4750 N，对应的吊具吊点的不均匀系数为1.04。

3.4 各因素叠加后的影响

以上计算仅针对吊具一个吊点(前左)长度存在偏差时，对各点受力与对应的影响因素进行了分析，而由于吊带生产时的长度差随机性、使用装配时的位置随机性等原因，以下继续对该类型吊具四吊点受力不均匀影响因素和不均匀程度进行分析。

由于该四吊索吊具前后吊点的长度不一致，因此吊具与前述两种吊具的结构特点和承载特性也不一样，对吊具的计算工况应进行分析和区分。根据吊具结构特点，以前左吊带偏长0.04 m为例，对质心偏差(+0.1、0.01)的情况进行分析，前左、前右吊带偏差0.04 m，前左、后右吊带偏差0.04 m计算。

分别对上述的两种情况简称为组合一和组合二，对两种情况进行计算。经计算组合一的受力结果见图12，组合二在ADAMS计算时无法收敛、无法静平衡，即组合二的情况起吊时产品受力不平衡，无法顺利完成起吊。

通过对上述计算结果进行分析可得出以下结论：

1)组合二情况(对角线上两点偏长或偏短)无法静平衡，吊具在安装时应避免对角两点都偏长的情况；

2)组合一情况(同侧两点偏长)时，吊点的受力最大偏差3900 N，较之前的计算结果偏小，因此该工况的影响因素也较小，由此计算的吊点受力不均匀系数为1.03。

图12 组合一各吊点受力情况

3.5 小结

通过使用ADAMS动力学分析软件对该四吊索吊具进行受力分析，可得出以下结论：

1)单梁四点沿产品轴向斜拉起吊类型的吊具受力均匀性影响因素包含吊索伸长率、吊索长度差、被吊产品质心位置偏差、吊索安装组合位置等；各影响因素的影响因子从大至小排序为被吊产品吊索安装组合位置>吊索长度差>质心位置偏差>吊索伸长率。其中对角两点吊索均偏长或偏短时，吊具的受力不能静平衡，在使用时应避免。

2)根据吊具计算结果，受力不均匀系数最大为1.04，后续受力不均匀系数可按1.05进行计算分析。

4 结论

本文从单根吊索长度差、吊索伸长率、质心偏差和各综合因素叠加等四个角度分别进行了起吊不均匀性的仿真计算。经过仿真计算，可以得出以下结论：对该四吊索吊具，其为框架式单梁四点沿产品径向斜拉起吊类型的吊具，明确被吊产品吊索安装组合位置对提高起吊均匀性有重要意义。但是吊索的伸长率特性对起吊均匀性作业不大。在各种因素叠加作用下，吊点的不均匀系数最大不超过1.04，后期针对此种类型的四吊索吊具可以将不均匀系数降低到1.05，这样可以有效减轻吊具的重量。