双曲柄机构的可视化研究与分析
周启兴
1 引言
双曲柄机构常作为往复运输机、多杆压力机的主运动链。由于它有急回特性、能提高工作效率,又被广泛地应用于诸如惯性筛、刨床、插床等机械中[1]。机构运动分析可为机构设计和机构动力学分析提供重要数据,如国内学者[2]发现双曲柄调距功能满足正弦规律,为新型垂直轴风力发电机的研发打下了基础;文献[3]根据插床插刀的位移、速度等曲线,判断插床六杆机构运动副所受摩擦总反力的方向。连杆机构的运动分析方法很多,光用数学解析法存在工作效率低、不形象直观等问题,实验法、图谱法设计精度较低[4]。随着机构运动仿真软件的推行,利用计算机仿真技术对平面连杆的研究和成果越来越多[5-7],特别在机构的可视化方面,如文献[8]通过VB对偏置曲柄滑块机构的位移、速度和加速度进行了可视化分析;文献[9]利用Matlab对连杆机构的杆单元各点应力进行了可视化后置处理。很多研究表明,可视化界面友好,对产品开发、辅助设计和分析能提供很大帮助[10]。目前,对双曲柄机构的研究主要集中在行程速比系数、急回特性、运动特性等方面,可视化分析的文章较少。
LabVIEW是一种图形化软件,可视化效果非常好。通过建立双曲柄机构运动学方程,借助LabVIEW编程,设计了其运动参数实时显示的运动数值分析界面,实现了从动曲柄角位移、角速度、角加速度及其最大值、最小值的可视化显示,并研究了杆长参数对双曲柄机构运动数值的影响。
2 双曲柄机构的数学模型
双曲柄机构运动简图,如图1所示。建立坐标系xay,设lab,lbc,lcd,lad为各杆件长度 ψ1,ψ2,ψ1分别为杆件 ab、bc、cd 与 x方向的夹角。
把机构当作一个封闭矢量,则得到矢量方程:

消去整理得:
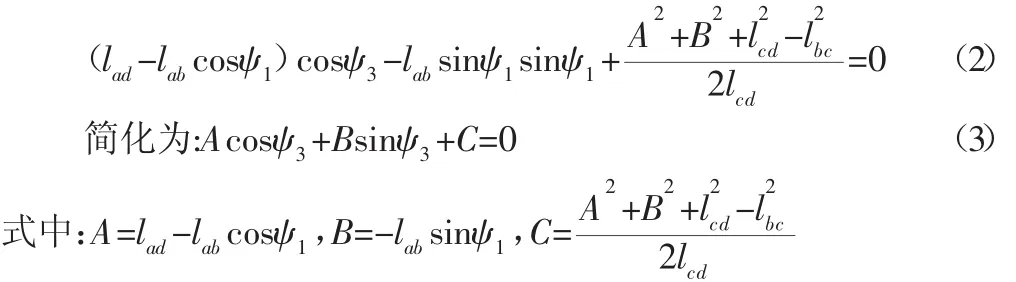
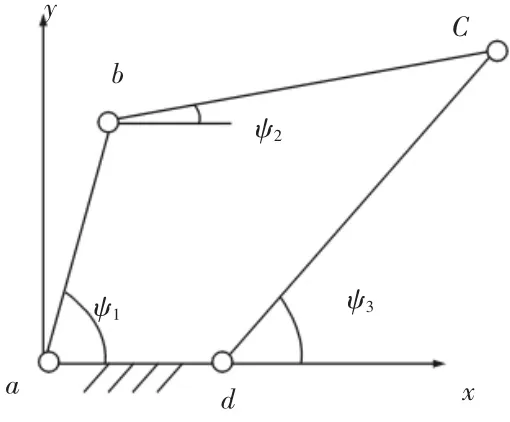
图1 双曲柄机构简图Fig.1 Schematic Diagram of Double Crank Mechanism

将式(4)、式(5)代入方程(3),整理得:
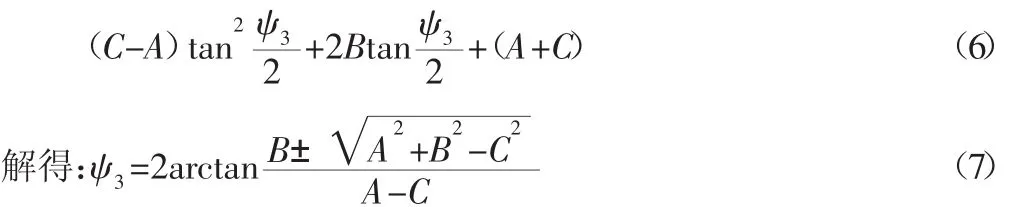
由机构的实际运动情况可知,从动曲柄的角位移ψ3的取值为:

式中:P12、P23、P34、P14、P13、P24—双曲柄机构 abcd 中的 6 个瞬心,
如图2所示。辅助线bb′、cc′均垂直于lad。
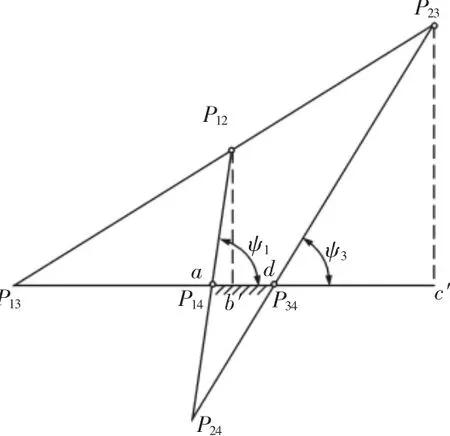
图2 双曲柄机构的瞬心Fig.2 Instantaneous Center of Double Crank Mechanism
直角三角形Δabb′和Δdcc′中边长满足

又因为 ΔP13bb′∽ΔP13cc′,故:

整理后为:

3 机构可视化设计的实现
双曲柄机构可视化设计采用LabVIEW编程实现,程序框图,如图3所示。采用LabVIEW图形化编程中的for循环结构、数值运算、公式节点、数组、数据筛选、数据类型转换、波形数据输出等模块来实现,其中for循环次数设置为360。双曲柄机构主动曲柄、连杆、从动曲柄及机架的杆长分别用a、b、c、d来表示,用n表示主动曲柄的转速,x表示主动曲柄的角位移,这些都作为输入量;主动曲柄的输出用y0(输出范围定为0~2π)表示,从动件角位移、角速度、加速度分别用y2(y1表示弧度制角位移,输出范围:-π~π)、y3、y4作为输出,当输入杆长 a=160mm、b=180mm、c=90mm、d=50mm时,主动曲柄转速n=65 r/min时,运行程序,得到的曲线,如图4所示。图4是程序前面板,该界面显示主动件在一个周期内的角位移变化情况和从动曲柄随主动件角度变化的角位移、角速度、角加速度曲线,直观地显示了该双曲柄机构的运动规律。程序运行后,波形数据同时显示在数组里面,同时通过写入电子表格程序,又保存在.exl文件格式中。在数据输出方面,程序设计了波形图、数组、最大值、最小值筛选处理,最大值通过量表实时动态显示,可有效直观地显示双曲柄机构的运动学数据。

图3 程序框图Fig.3 Block Diagram of Program
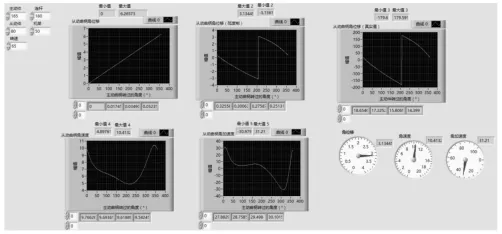
图4 程序前面板Fig.4 Front Panel of Program
4 杆长参数对双曲柄机构运动学数值的影响研究
4.1 参数设置
构件本身有制造误差,构件安装也有误差,因此分析杆长尺寸变化(包括误差引起的变化)对双曲柄机构运动特性的影响显得很有必要。
采用单独改变某一杆长参数来研究其对从动曲柄角速度、角加速度的极值的影响,参数设置,如表1所示。采用四种方案进行。改变参数,运行程序,由于得到从动曲柄角位移最大值都是3.14(180°),这里不分析从动曲柄角位移的问题。
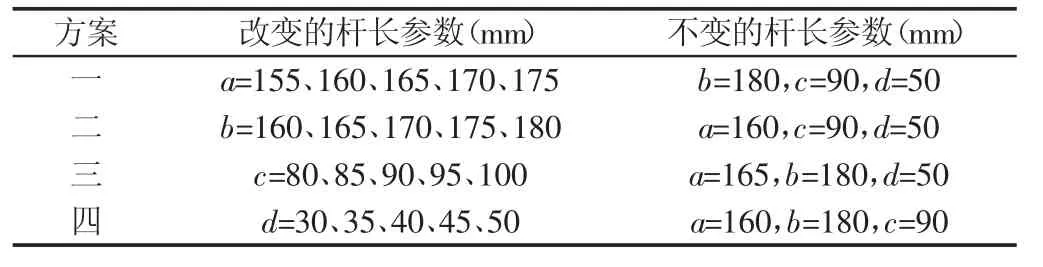
表1 杆长参数Tab.1 Parameters of Rod Length
4.2 结果分析
方案一得到的结果,如图5所示。从图5可以发现双曲柄机构主动件长度增加时,其从动曲柄的角速度最小值、最大值都减小,角加速度的最小值、最大值的绝对值都减小。
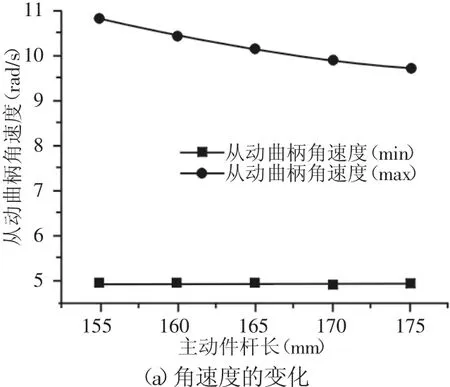
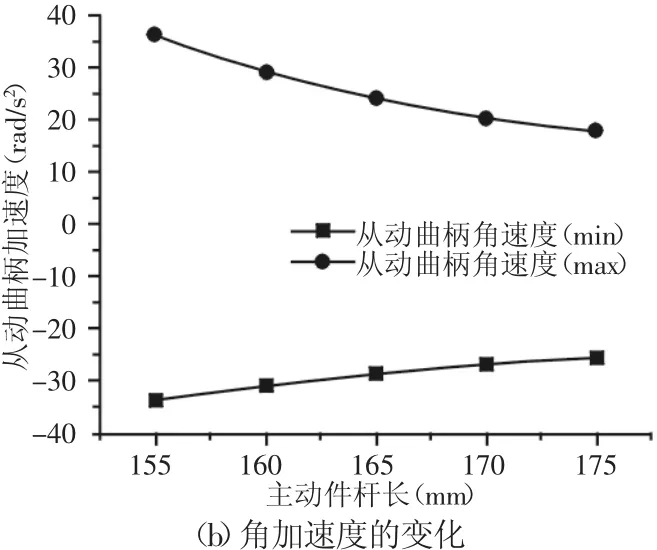
图5 主动件长度对从动曲柄的影响Fig.5 Effects of Active Part Length on Driven Crank
方案二的结果,如图6所示。从图中可以看出,连杆长度增加时,从动曲柄的角速度最小值、最大值都增大,角加速度的最小值、最大值的绝对值都增大。
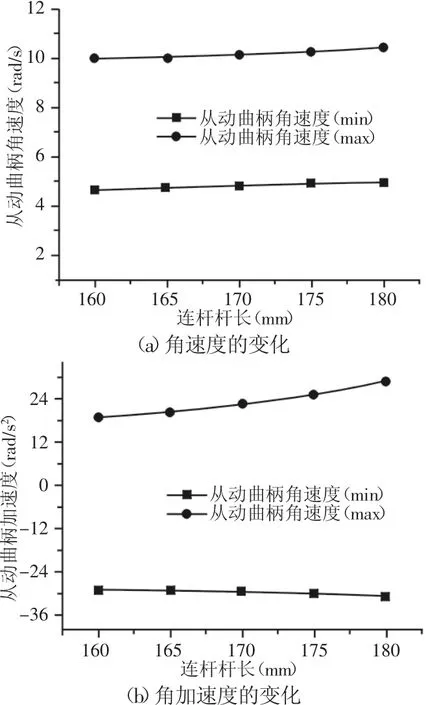
图6 连杆长度对从动曲柄的影响Fig.6 Effects of Connecting Rod Length on Driven Crank
方案三的结果,如图7所示。可知从动曲柄杆长增加时,从动曲柄角速度最小值增加、最大值减小,从动曲柄角加速度最大值、最小值的绝对值均减小。方案四的结果,如图8所示。机架长度增加,从动曲柄角速度、角加速度最小值、最大值都变化明显,角速度随机架长度增加,最小值减小、最大值增大,角加速度最小值、最大值的绝对值都增加。
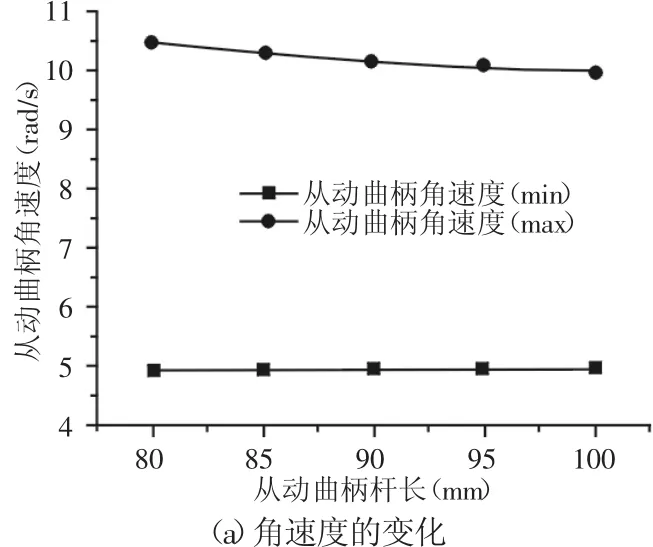
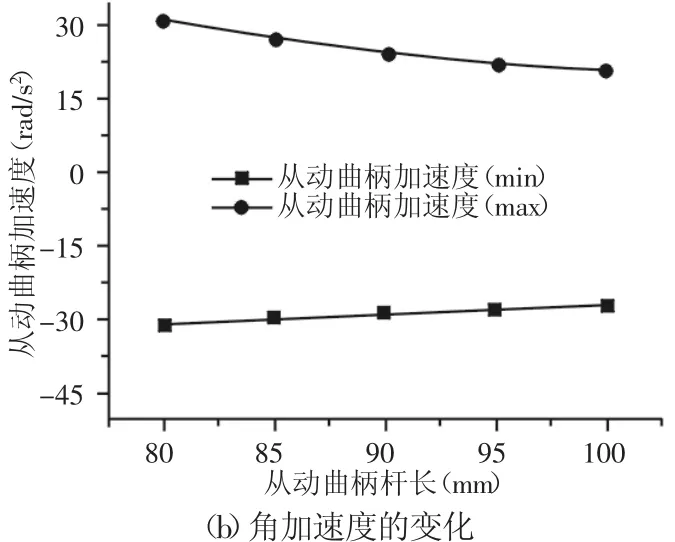
图7 从动曲柄长度对从动曲柄的影响Fig.7 Effects of Follower Crank Length on Follower Crank

图8 机架长度对从动曲柄的影响Fig.8 Effects of Frame Length on Driven Crank
从四种方案结果来看,单独增加某一杆长参数,从动曲柄角速度、角加速度都呈现有规律的递增或递减,机架参数对其的影响最为明显。角加速度的变化直接影响机构的急回运动和冲击振动,该研究结果对具有双曲柄机构的机器的方案设计及动力学分析可提供帮助。
5 结论
(1)通过LabVIEW软件编程得到了双曲柄机构运动参数的可视化界面,提高了机构分析效率,让数据分析过程更有效、直观。(2)利用分析界面得到了杆长参数对双曲柄机构的运动输出的影响。杆长参数变化,从动曲柄角速度、角加速度都呈现一定规律递减或递增,机架参数对其影响最为明显。为双曲柄机构的设计、动力学计算提供理论参考。

