废旧机床再制造方案的三维矢量评价模型
程 宏,江志刚,张旭刚
1 引言
目前,我国机床保有量已高出700万台,其中60%以上的机床服役周期达到10年,在接下来的5至10年内这些机床都有可能面临维修甚至直接报废的处理方式[1]。若对这些机床全部进行淘汰处理,会造成大量的资源浪费,同时也需要大量的资金[2]。若对这些废旧机床进行再制造处理,其性能能够恢复甚至超过原有机床性能,且成本仅为新品的50%左右[3]。因此,对废旧机床开展再制造能有效减少制造机床的资源浪费。
由于废旧机床失效特征和损伤形式的不同,废旧机床实施再制造时方案具有多样性,而不同的再制造方案又会影响再制造的成本、时间和质量,因此,选择最佳的机床再制造方案是节约再制造成本,提高再制造产品质量,实现机床再制造资源最优化重用的重要途径。国内外对废旧产品再制造方案评估开展了系列研究并取得了一定的成果,如文献[4]结合再制造工艺过程,构建了与加工能力、加工时间和加工设备等有关要素的线性优化模型,并采用仿真技术验证优化结果;文献[5]结合再制造工艺过程,建立了加工成本和加工批量之间的混合整数优化模型,并对它们之间的相互关系进行了讨论;文献[6]分析了再制造工艺技术的影响因素,并在此基础上构建了多目标决策模型,从而优化决策再制造技术方案;文献[7]结合机床导轨的特性,利用专家知识和模糊理论的方法构建了一种再制造过程优化模型。综上所述,现有研究主要集中在废旧产品再制造方案评估,且大部分成果是以再制造方案已知为前提条件,进而研究再制造时间、技术和工艺参数,很少涉及机床再制造领域,特别是废旧机床再制造方案的评价[8]。为实现废旧机床再制造经济效益与环境效益的协调优化,需要从技术、经济和资源环境等三维维度建立废旧机床再制造的评价指标体系。此外,废旧机床再制造方案的三维评价既要追求三个方面都取得显著效果,还应保证评价指标体系间的协调统一,为此,提出基于矢量分析法的废旧机床再制造方案评价模型,在整体方案评价的基础上考虑指标间的静态与动态协调性评价,进而选择废旧机床再制造的最佳方案,为废旧机床再制造提供依据。
2 废旧机床再制造方案三维评价指标体系
在实施不同的再制造方案时,污染物的产生和排放一般来源于材料和能源的消耗,而材料和能源的消耗是受再制造过程中技术、成本、资源环境等参数的影响。为此,从环境的角度构建了一种废旧机床再制造方案评价体系,如图1所示。

图1 废旧机床再制造方案的评价体系Fig.1 A Evaluation System of Used Machine Tool Remanufacturing Scheme
2.1 废旧机床再制造方案评价指标的量化方法
2.1.1 技术性指标
技术性指标是保证废旧机床再制造后获得比原机床更好的质量和可靠性,主要包括精度指标、效率指标、功能指标和可靠性指标。技术性指标可采用式(1)进行计算:

式中:μ1,μ2,μ3,μ4—精度指标系数,效率指标系数,功能指标系数,可靠性指标系数;ω1,ω2,ω3,ω4—μ1,μ2,μ3,μ4的权重。
(1)精度指标系数μ1
精度指标表示废旧机床经过该再制造方案后在加工精度方面所具有的水平。机床再制造后的精度指标值为向量A={a1,a2,…,an};机床再制造之前的精度指标值用向量C={c1,c2,…,cn}表示;机床精度比较值用向量D={d1, d2,…,dn},所组成的机床精度评语集为{很差,差,一般,好,很好},其相应数值大小为{0.2,0.4,0.6,0.8,1}。定义精度评估指标为R={r1, r2,…,rn}:当 di≤0 时,精度等级很好,ri=1;当 0<di≤0.05 时,精度等级好,ri=0.8;当 0.05<di≤0.1 时,精度等级一般,ri=0.6;当 0.1<di≤0.2 时,精度等级差,ri=0.4;当 di>0.2时,精度等级很差,ri=0.2。精度指标在进行综合评估时,各项指标相应的权重组成向量 B={b1,b2,…,bn},其中 bi表示对第 i项指标ri的权重系数,进行归一化处理床技术性评估可由下式计算:

式中:“·”—矩阵数量乘。
(2)效率指标系数μ2
效率指标表示废旧机床经过该再制造方案后,机床加工增加的效率。由于在废旧机床再制造方案拟定阶段,机床再制造效率的提高难以得到,需要借鉴专家打分的方式,因此,效率指标所构成的评语集为{很低,低,一般,高,很高},相对应数值为{0.2,0.4,0.6,0.8,1}。
(3)功能指标系数μ3
功能指标表示经过该再制造方案,机床功能上增加的能力。综合考虑再制造机床能实现的各项功能,可知功能指标系数μ3由下式(3)计算。
式中:k=1,2,…,n;n—功能的总项数;μ3k—第 k 项功能的指标值,如果具备该功能,则 μ3k=1;否则,μ3k=0;ω3k—第 k 项功能的权重,需要依据客户的要求来确定。(4)可靠性指标系数μ4
可靠性指标指废旧机床经过该再制造方案,在相应的时间和条件下,无故障的实现加工任务的可能性。而在废旧机床再制造方案拟定阶段,机床再制造的可靠性难以得到,需采用专家评价法,因此,可靠性指标所构成的评语集为{很差,差,一般,好,很好},相对应数值为{0.2,0.4,0.6,0.8,1}。
2.1.2 经济性指标
经济性指标的目的是通过较少资金投入来获得高性能的机床,因此,废旧机床再制造方案的经济性指标主要从成本方面考虑。机床再制造成本Cm主要由回收成本c1、再制造成本c2和废旧机床再制造的其他成本c3组成。
在文献[9]中提到,再制造后的产品或价格若是新产品的(40~70)%,再制造企业将获得利润。
通过对机床企业大量调查可知,若D小于40%,企业会得到丰厚的利润;若D高于60%,企业将因缺乏市场竞争力,而得不到利润。因此,经济性指标C定义为一个与D有关的函数,如式(5)所示。
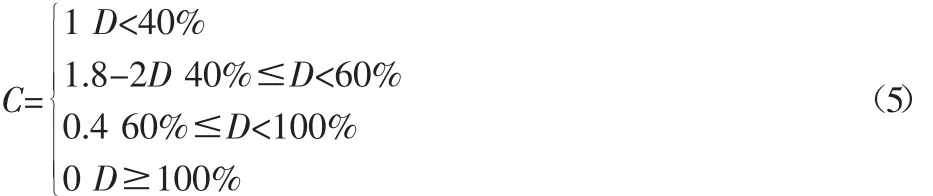
2.1.3 资源环境性指标
废旧机床再制造方案资源环境性评价指标主要是从资源节约和环境影响两个角度进行考虑。废旧机床再制造与原产品制造相比,其资源环境影响减少具体表现形式为资源节约、能耗节省和污染减少。因此,资源环境性指标可有下式表示:

式中:μm,μe,μp—资源节约指标系数,能耗节省指标系数和污染减少指标系数。ωm,ωe,ωp则为:μm,μe,μp的权重。
(1)资源节约指标系数μm
废旧机床再制造过程中大量采用废旧零部件及修复完成后能再次利用的零件,因此最大程度上节约了资源。资源节约指标公式如下:

式中:Qrm—机床再制造中可再制造的数量;Qru—机床再制造中可直接利用的数量;Q—机床再制造整体数量。
(2)能源节省指标系数μe
机床再制造过程中采用的大量都是原产品零部件,不需要新的原材料,避免了大量的能源消耗,用式(8)来评价能源节省指标:

学校虽然是学生德育的主渠道,但仅靠学校自身的力量是远远不够的。因而学校要以大德育观为工作思路,使家庭、社会等各种教育力量都参与到网络德育工作中,形成学校、家庭、社会三位一体的德育教育格局,使三者在教育功能上取长补短,互为补充,相得益彰,产生整体效应,为中学生的健康发展构建和谐的平台。
(3)污染减少指标系数μp
污染减少指标不能简单的用数学公式对其表示,需采用专家评判的方法进行量化处理,量化结果与影响机床再制造方案评价的重要程度相对应:影响程度很大(1),影响程度大(0.8),影响程度一般(0.6),影响程度小(0.4),影响程度很小(0.2)。
3 基于三维矢量的废旧机床再制造方案评价模型
废旧机床实施再制造时应在技术、经济和资源环境三方面同时取得良好的效应,而目前,许多再制造评价决策问题讨论的是各指标功能之和,却很少对评价指标间的协调统一进行探讨,造成再制造后的机床整体性能和企业不能同时达到最佳效益。矢量分析法具有算法简单、应用广泛等特点,能快捷地对指标进行定性和定量的表达。因此,引入矢量分析法,建立基于三维矢量的废旧机床再制造方案评价模型,对整体再制造方案评价矢量的大小和作用方向进行分析,然后,针对再制造方案评价指标产生的大小变化,进行再制造方案的静态协调性评价和动态协调性评价,以寻求评价指标间协调和整体再制造方案的最优,为机床厂开展方案评估和指导改进提供一种新的决策途径。
3.1 建立再制造方案评价的空间几何模型
为快捷选择废旧机床再制造方案,把这三个评价指标当作空间的三个维度,建立再制造方案评价的空间几何模型,如图2所示。
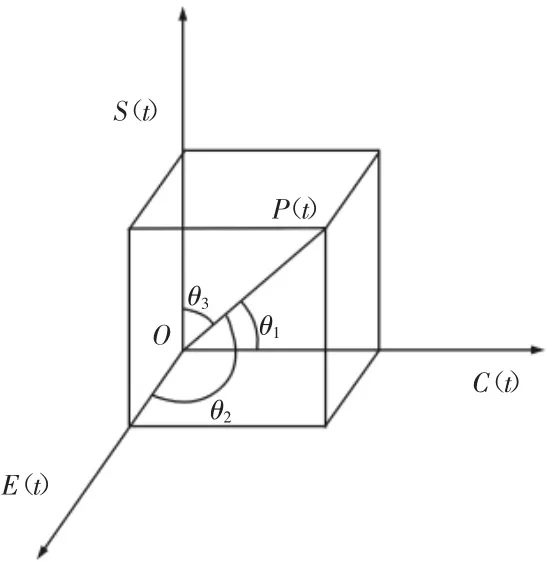
图2 废旧机床再制造方案评价的空间几何模型Fig.2 Space Geometric Model of Used Machine Tool Remanufacturing Scheme Evaluation
经济、技术和资源环境三个方面的评价值作为评价废旧机床再制造方案在 t时刻的三维矢量,分别用 C(t),E(t),S(t)表示,根据平行四边形原则,对这三个矢量进行求和便可获到废旧机床再制造方案评价的整体矢量O■→P,P(t)便是其合成值。每一个在矢量空间中的点都是一个特定状态的点,废旧机床再制造方案评价就被直接地划分为这空间几何中的状态点,即点 P(C(t),E(t),S(t))。由此,废旧机床再制造方案评价就转化为空间几何中三维向量求和。根据空间向量可知,废旧机床再制造方案评价的三因素与整体评价之间的关系可以用函数式来指代,函数式的公式如下:

3.2 废旧机床再制造方案的静态协调性评价
废旧机床再制造方案的协调性评价分为静态协调性和动态协调性两种评价方式。
时间点t的三维矢量均衡状态称作静态协调度,静态协调度可以凭借空间几何中整体矢量和三维矢量间所夹夹角的大小及方向来表示。根据三维矢量分析法的要求,再制造方案的三个指标分量应有相同的重要度,不能偏离或偏废某一个分量,需要全面协调的发展以达到整体最优的效果,因此废旧机床再制造方案评价的静态协调性计算方法采用乘法合成法来反映,如式(10)所示。

3.3 废旧机床再制造方案的动态协调性评价
动态协调度表示三维分量在废旧机床再制造方案评价中趋于有序方向的动态发展程度,主要包含:再制造方案评价指标产生的大小变化和静态协调性的改进。所以,动态协调度的计算要综合考虑整体评价值的大小和三维矢量的变化趋势,具体计算,如式(11)所示:
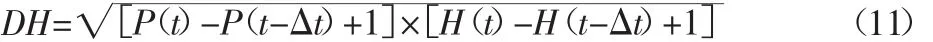
式中:DH—静态协调度,其值越大表示废旧机床再制造方案的动态协调程度越高。
3.4 基于三维矢量的废旧机床再制造方案评价模型
基于三维矢量的废旧机床再制造方案的评价模型由三维矢量的整体发展水平,静态协调度和动态协调度构成,具体计算公
式中:F—再制造方案综合评价值;P(t)—再制造方案整体评价值;H—静态协调度;DH—动态协调度。
当0.60≤F≤1时,废旧机床的再制造方案很好;当0.3<F<0.60时,废旧机床再制造方案一般;当0<F≤0.3时,废旧机床再制造方案差。
4 案例分析
随着现役机床服役年龄和客户需求功能增加,某机床厂的大量车床已不能满足企业使用要求。为了有效改善这种现状,该机床厂拟定了两套再制造方案,现需对两套方案进行评价选择,两套方案,如表1所示。根据所构建的指标量化方法,对拟定的两种废旧机床再制造方案进行评估,其计算结果,如表2所示。
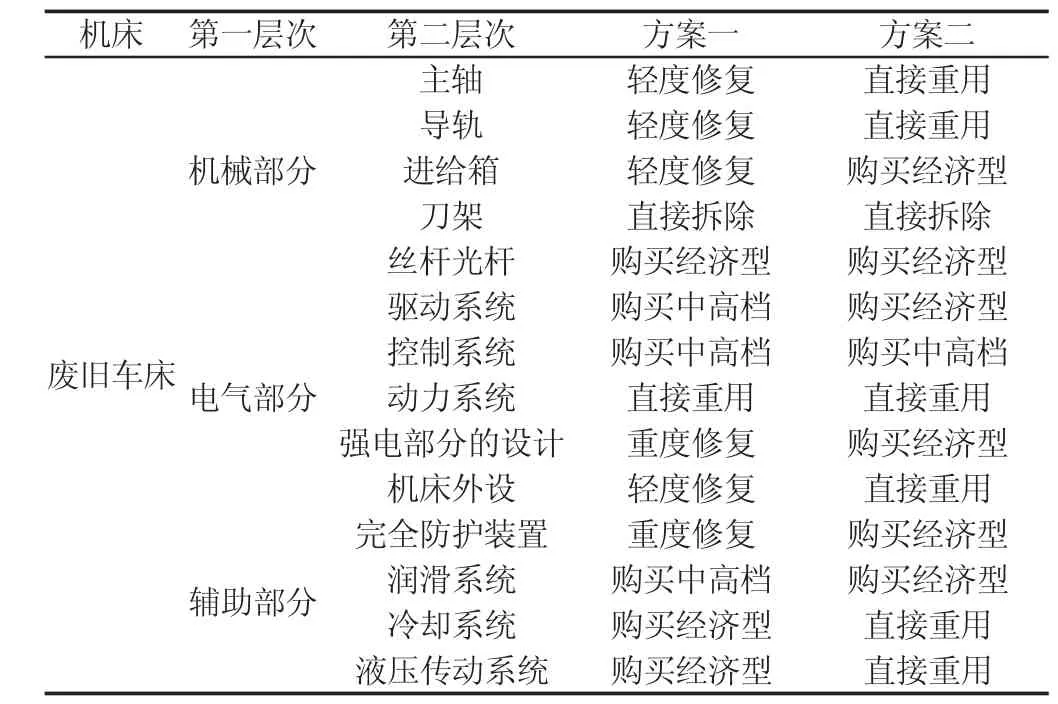
表1 车床再制造方案Tab.1 Lathe Remanufacturing Scheme

表2 机床再制造方案评价指标值Tab.2 Machine Tool Remanufacturing Scheme Evaluation Index
由以上分析可得,废旧机床再制造方案1和2的整体评价值分别为1.247和1.270。再通过式(10)、式(11)、式(12)分别计算两个方案的废旧机床再制造综合评价值,方案1=0.762;方案2=0.719。从以上结果可知,使用方案2再制造时,废旧机床的整体评价值大于方案1,表明方案2的整体性强于方案1。然而,方案1的再制造综合评价值要大于方案2,表明采用方案1再制造时,机床取得良好整体效果的同时各指标都能协调有序,以达到最佳效果,从而保证机床的可持续发展。因此,基于三维矢量的废旧机床再制造方案评价模型能更有效地帮助机床厂评估出再制造方案的优劣。
5 总结
构建了废旧机床再制造方案评价指标体系,并对指标进行量化分析;建立了一种基于三维矢量的废旧机床再制造方案评价模型。该模型能更有效、可靠地评价废旧机床再制造方案。但是,随着再制造业的不断发展,必然会出现新的评价指标,因此需要建立更为合理的指标体系及再制造方案评价模型,使其能更加准确地评价机床再制造方案指标间的协调性,为再制造方案选择提供依据。

