深入挖掘题目内涵 平凡中彰显不平凡*
——基于2018年浙江省数学高考试题第20题
●金灿芳 (萧山中学,浙江杭州 311200)
1 考题再现
题目已知等比数列{an}的公比 q>1,且a3+a4+a5=28,a4+2 是 a3,a5的等差中项,数列{bn}满足b1=1,数列{(bn+1-bn)an}的前n项和为2n2+n.
1)求q的值;
2)求数列{bn}的通项公式.
(2018年浙江省数学高考试题第20题)
在数列{an}中,n∈N*,其中q为常数),则称{an}为等差比数列.
本题考查的是利用错位相减来求等差比数列的前n项和,全省的平均分不高,只有总分的一半.本题首先要利用数列{an}的通项an与前n项和,将条件转化成求等差比数列的前n项和,有很多学生这一关没有转化对;在具体求和时,错位相减的方法也有很多学生没有落实好.错位相减是数列求和问题的常规方法,可以将等差比数列的求和问题转化为利用公式求等比数列的前n项和.我们深入研究该题,还能挖掘出更多的内涵,这个数列可以利用待定系数求解,利用裂项相消求和,也可以构造成常数数列,还可以构造成等比数列,利用通项公式求解.
2 解法分析
解1)易得 a4=8,q=2.
2)由第1)小题易得 an=2n-1,令 cn=(bn+1-bn)an,则数列{cn}的前 n项和 Sn=2n2+n.由于因此 c=4n-1,代入得n.又 b-b是“差分”的形式,即nn-1bn=(bn-bn-1)+(bn-1-bn-2)+…+(b2-b1)+b1,从而

对于数列{anbn},其中{an}为等差数列,{bn}为等比数列,设 an=a1+(n -1)d,bn=b1qn-1(其中q≠1),求数列{anbn}前n项和的关键是求数列{nqn-1}的前 n 项和.令
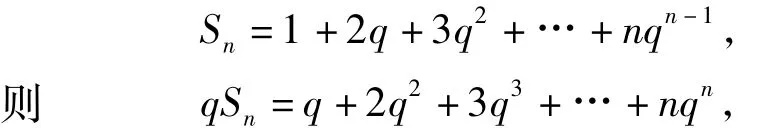
两式错位相减,得
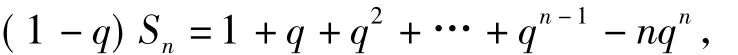
移项得

综上可知,利用错位相减的方法,任意等差比数列的前n项和都可以转化成求等比数列的前n项和.
3 解法探究
3.1 构造一般模型

3.2 构造裂项相消


事实上,在本题的已知条件下,b1的值一定满足数列{bn}的通项公式,根据裂项相消的特点,可将 b=1 代入,得 C=15,即1

在这个解法中裂项相消的构造是重要思想.第二种构造大大地简化了过程,并且在这样的构造下,通项公式的主要形式已经明确,因此可以用待定系数法迅速求解,与“构造一般模型”的思想类似,但是这样的技巧需要平时的沉淀和积累.第一种构造是从一般入手,只要等差比数列或等比数列的通项都可以去尝试,如在等比数列中,qn=不妨令 an=(xn+y)qn,因为(n+1)qn+1-nqn=nqn(q-1)+qn+1,所以

则an就表示成了裂项相消的形式.除此之外,裂项相消的一般形式还有以下4种:
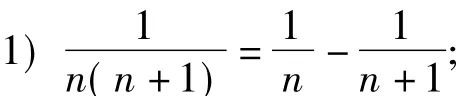
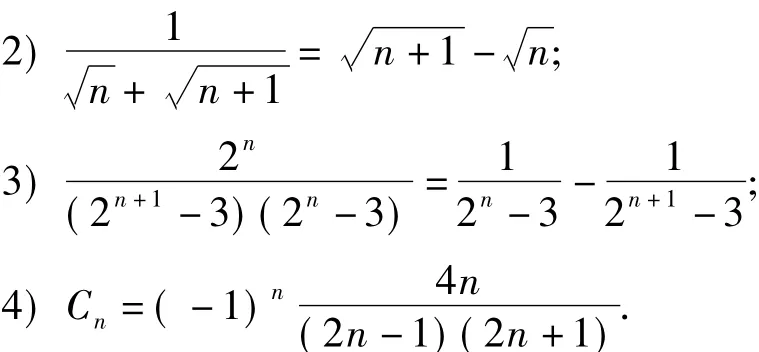
3.3 构造常数数列

这个解法是建立在已经构造好裂项相消的基础上,本质还是构造裂项相消,若 an-an-1=f(n)-f(n-1),则
an-f(n)=an-1-f(n-1)=…=a1-f(1),从而{an-f(n)}为常数数列,即可求出{an}的通项公式.
3.4 构造等比数列
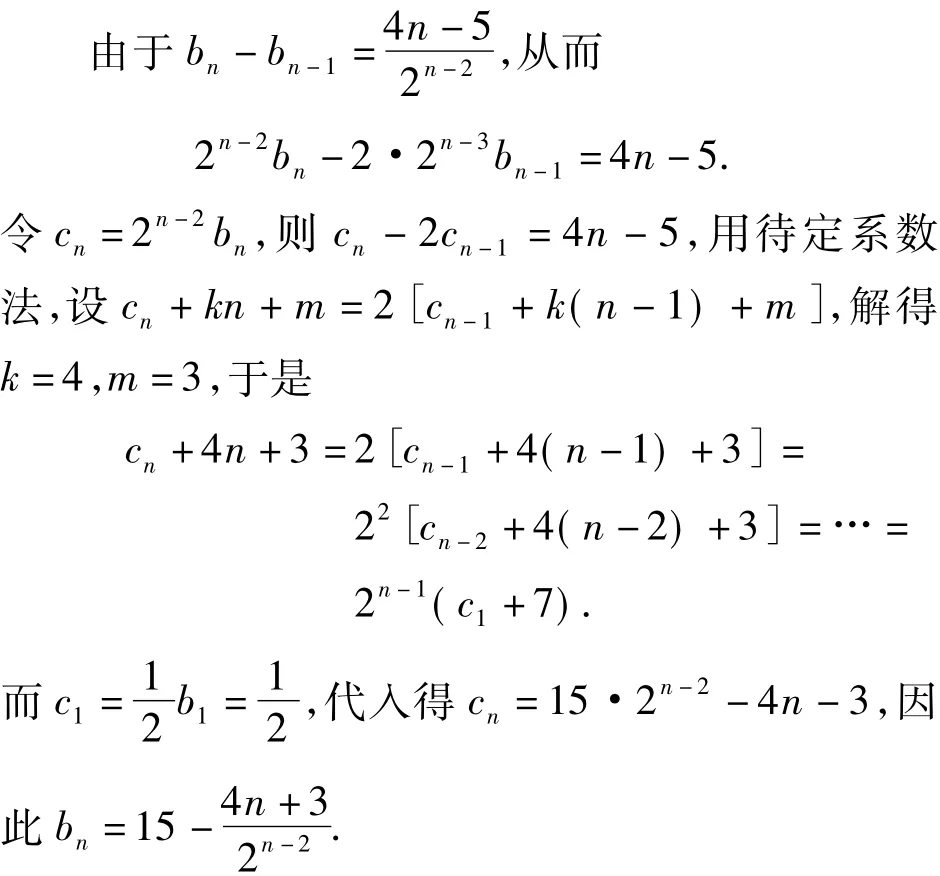
用构造法求数列的通项公式是数列中的重要知识点,常见的有以下3类:
1)an=pan-1+q,令 an- m=p(an-1- m),解则{a-m}是首项为 a-m、公比为pn1的等比数列.
2)an=pan-1+qn+r,令 an+xn+y=p[an-1+x(n-1)+y],解得于是构造了新的公比为p的等比数列,这就是本题的类型.
4 结束语
本题主要考查利用错位相减来求等差比数列的前n项和,深入研究可知方法不止一种.除了落实错位相减的方法,还可以向学生灌输待定系数的方法和数列中其他的重要思想,比如从一般的、常见的裂项相消开始,能够辨析一些复杂的裂项相消;不仅可以解决一次函数型的由递推公式求通项公式,也能解决带n的或指数型的由递推公式求通项公式.
我们的教学主要是例题教学.优质的试题,通过教师的思维引导和解法展示,资源得到了充分的利用,达到了训练的目的,也能适度减轻学生的负担[1].在解题教学中要注重学生的解题思维,挖掘其中的知识点,让学生在读题、析题、解题、悟题的过程中提升自己的数学思维素养[2].
这就要求教师要充分地研究题目,分析条件,挖掘各种有效的解题方法,有些看似平凡的题解法丰富,能让学生有效地落实各种相关知识点,在解题思维中彰显它的不平凡.

