新高考背景下创新试题的命制历程*

●任伟芳 (宁波市教育局教研室，浙江宁波 315000)

提出一个问题往往比解决一个问题更为重要，因为解决一个问题也许只是一个数学上或实验上的技巧问题．而提出新的问题、新的可能性，从新的角度看旧问题，却需要创造性的想象力［1］．提出问题需要创新能力，因而命制一个问题比解决一个问题更加困难，充满着不可预知的魅力，也向无数喜爱命题的研究者及一线教师提出了挑战．为了促进教师的专业成长，掌握科学命题的基本原理和方法，提高考试命题的技术和水平，发挥以评价引领课堂教学的作用，近日浙江省宁波市教育局教研室开展了以“新高考背景下的创新试题命制”为主题的教学比武活动，一线数学教师踊跃参加，颇受好评．下面笔者整理了命制受到较高评价的部分试题以及近几年对试题命制方法的一些感悟，以例谈的方式与各位同行交流命制试题的过程，敬请批评指正．

1 改编教材题目

教材是“教师教”和“学生学”的主要凭借，是教师进行教学的具体依据，是学生获得系统知识、发展智力、提高素养的重要工具．教材中有很多体现核心知识、基本方法的学习内容，也有很多经典的例题、习题．可以根据需要，通过变更问题的结构、改变题设的数据和设问方向等来改编教材题目．

1．1 题目来源

例1设点 A，B的坐标分别为(－5，0)，(5，0)，直线AM，BM相交于点M，且它们的斜率之积求点M的轨迹方程．

(人教A版《数学(选修2-1)》第41页例3)

我们一再地改变它、重新叙述它、变换它，直到最后成功地寻到某些有用东西为止［1］．因此旧的问题解决后再从新的角度多方向探究问题，对设计发现新问题来说显得弥足珍贵．

探究方向1探索特殊到一般是否成立．

改编1设点A，B的坐标分别为(－a，0)，(a，0)，直线AM，BM相交于点M，且它们的斜率之其中a＞0，b＞0)，求点M的轨迹方程．

改编2设点A，B是椭圆(其中a＞b＞0)上关于坐标原点O对称的两个点，点M是椭圆上异于点A，B的任意一点，记直线AM，BM的斜率分别是k1，k2，问:k1k2是否为定值?

证明设 A(x1，y1)，B( － x1，－ y1)，M(x0，y0)，则

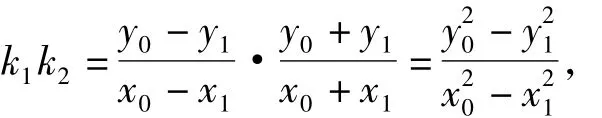
又点A，B，M在椭圆上，从而

结论1设AB为任意一条过椭圆(其中a＞b＞0)中心的弦，点M为椭圆上异于A，B的任意一点，若直线AM，BM斜率存在且记为k1，k2，那么k1k2为定值

探究方向2探究逆命题是否成立．

改编3已知点M(x0，y0)为椭(其中a＞b＞0)上任意一点，直线AM，BM分别交椭圆于点A，B，直线AM，BM 的斜率分别为k1，k2，满足，求证:直线AB过椭圆中心O．

证明直线AM的方程为

结论2已知椭圆(其中a＞b＞0)，椭圆一条弦的两个端点与椭圆上任意一点连线的斜率之积为充要条件是这条弦经过椭圆中心．

探究方向3探究定值为何是

结论3当变换T将圆变换为椭圆时，k1k2=－1仍成立．

结论4当变换T将直线变换为直线，变换后直线的斜率是原直线斜率的倍，记经过变换T后直线AM，BM的斜率分别为

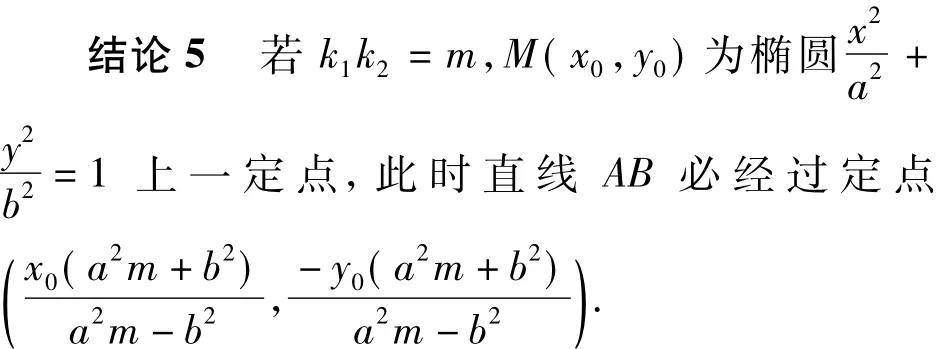
1．2 创新题目

例2已知椭圆，过点M的两条弦AM，BM的斜率之积为1，则直线AB过定点______．

分析设直线AM的斜率为k1，可表示出点A的坐标，同理可表示出点B的坐标，进而求出直线AB的方程，最后得到定点

评注本题考查椭圆的几何性质、圆锥曲线中斜率定值问题等知识点，命题考查的立意是提升学生数学运算、逻辑推理等数学核心素养以及数形结合的能力．本题难度系数为0．65，考试后的统计结果与考前预测相吻合．

1．3 命制说明

通过对例1中条件、结论的一般化以及条件与结论的位置互换，利用高等代数中的矩阵变换知识，最后得到了一道考查圆锥曲线定点的题目，达到了举一反三、触类旁通的目的．通过将例1改编成例2可知:在往年全国各地的数学高考题中，有时会发现有一些题目有教材中练习题、例题的影子，因此在平时的教学中，应好好利用教材中的资源和素材进行发散和探究．一个简单问题的一般化、条件互换就可以获得很多新的资源，一道题的发散是多方向的，要根据命题目标来确定这道题的关注点在哪里．总之，根据教材中提供的素材编制创新试题，不仅遵循《普通高等学校招生全国统一考试大纲的说明》，符合《普通高中数学课程标准》，而且还能抵制题海战术，引导高三复习教学形成“重视教材和钻研教材”的良好风气．

2 类比原有考题

2．1 题目来源

研究历年全国各地的高考试题，会发现有些题目的数量关系包含着深刻的几何背景，考查数学思想方法有一定的典型性．可以利用数形结合揭示内在的本质，通过类比数量关系的几何意义构造新颖的数量关系进行设问，也可以通过改变设问的视角和方式进行编题．下面以2017年浙江省数学高考试题第15题为原型进行改编为例加以说明．

2．2 创新题目

例3已知向量 a，b，满足2|a+b|+|ab|=15，|a|=3，则|b|的最小值是 ______，最大值是______．

图1

解法1(利用平行四边形的性质与线性规划)如图1，设|a+b|=x，|a －b|=y，由平行四边形的四边关系可得

如图2，画出可行域为线段PQ(含端点)，因此可行域上的点到原点的距离的平方的最大值在点P处取到，最小值在点H处取到，即可得|b|的最大值为6，|b|的最小值

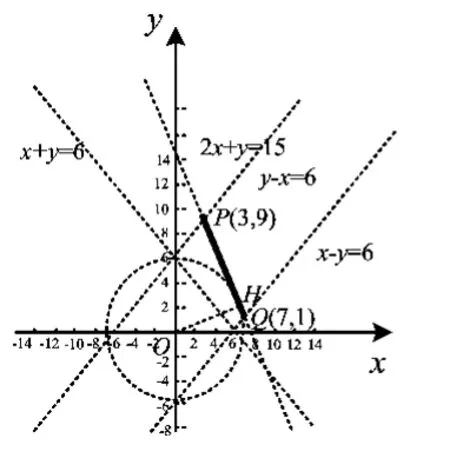
图2

图3

解法2(换元后求二次函数最值)如图3，设|a+b|=x，|a － b|=y，则

由平行四边形的四边关系可知

要求|b|的最值，即求x2+y2的最值．由三角形两边之和大于第三边，易算得 x∈［3，7］，则

从而

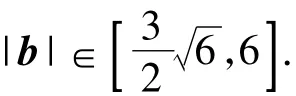
解法3(利用向量三角不等式与柯西不等式)由柯西不等式得

平塘县稻作区多丘陵山区，有较宽广的河谷地或盆地，阳光充足，水源较为方便，较适于杂草生长，主要草种有鸭舌草、牛毛草、稻稗、异型莎草、矮慈姑、青萍、眼子菜等20余种。实施稻鸭共育项目后，项目区杂草经鸭采食和踩踏，放鸭后40天左右，已基本无杂草，除草效果明显。另外，鸭的活动大大改善了稻田土壤的透气性，减轻了有毒物质的生成和危害，促进水稻根系的生长，从而利于水稻生长发育。

2|a+b|+|a －b|≤

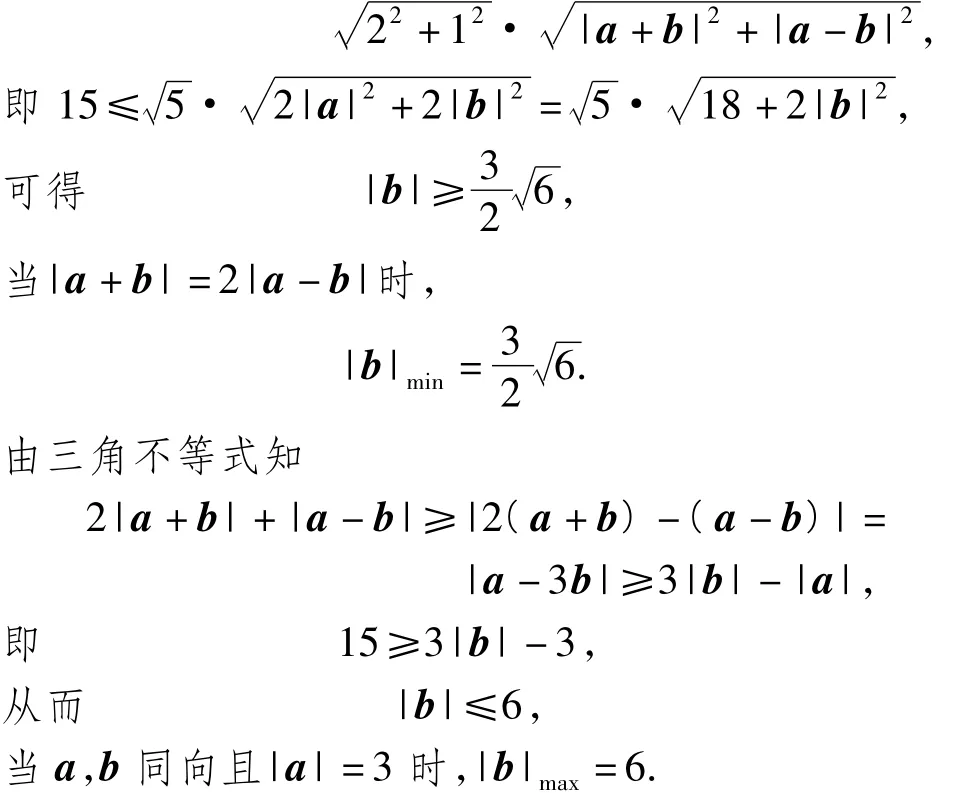
评注本题主要考查平面向量运算的几何意义、向量模的性质和三角不等式，以及推理运算、数形结合等一些基本的数学思想方法．“以能力立意”是命题者的指导思想，灵活多变的解题方法是本题命制的一大亮点．本题难度系数为0．55，达到预期目标．

2．3 命制说明

本题考查的基本意图是评价学生掌握平面向量加减法的概念及几何意义的程度．例3和高考真题的数学本质都是运用了“平行四边形的四边平方和等于两条对角线的平方”．命题者紧紧抓住这个结论巧妙地根据现有的试题类比改编成新颖问题，这已成为高考命题惯用的手法，我们几乎不能想象有一个问题是绝对的新颖，和我们以前所解决过的问题都不相似，都无关系［1］．作为数学教师应多研究高考真题，这样才能更好地把握高考的命题方向，如以向量加减法的三角形法则和平行四边形法则出发，通过置换结论和条件的方法可以延伸出很多问题，本试题成功改编就是一个精彩例证．

3 构造合理图形

构造是一种重要的数学思想方法，它是创造力较高的表现形式．在数学解题中，认真审题，依据题目条件，捕足“特征信息”，类比相关知识，构造数学模型，来寻求解题的切入点，从而可获得简捷、明快、新颖的方法．构造法是中学数学中最具有挑战性的解题方法，也是考查学生创新能力的最好载体之一．命题者要做有心人，做题留心方能偶得好题，正所谓:“踏破铁鞋无觅处，得来全不费工夫．”

3．1 命题来源

如图4，在正方体AEDF-BGHC中，边长为1，二面角D-CB-H的余弦值为，作 MQ⊥平面BGHC，Q为垂足．当MN⊥BC时，有

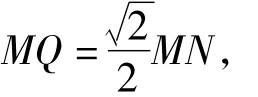
从而

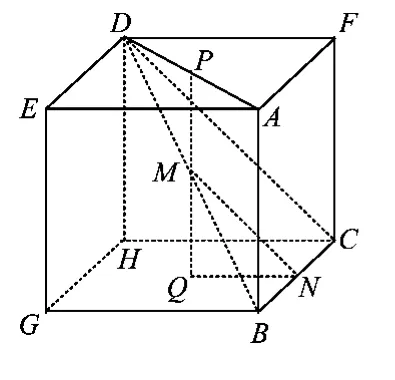
图4

图5

3．2 创新题目

解法2(构造三角形法)如图6，过点B作AD的平行线l，设dAD-l为平行线AD与l之间的距离，过点M作ME⊥BC于点E，过点M作MF⊥l于点F．因为

图6

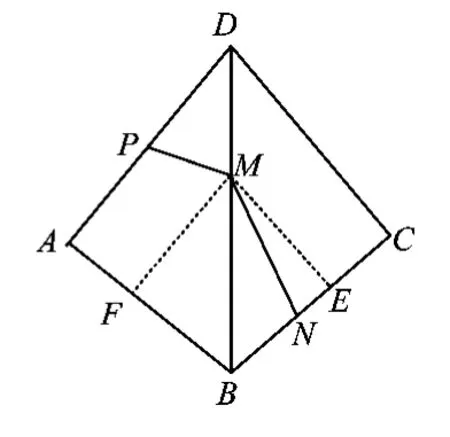
图7

解法3(构造全等形法)如图7，过点M作ME⊥BC于点E，作MF⊥AB于点 F．由于 BE=

推广在有公共斜边的Rt△ABD和Rt△CBD中，∠DAB= ∠DCB=90°，AD=CD=1，AB=BC=k(其中k为大于0的常数)，点P为AD的中点，点M，N分别在线段BD，BC上，求证:PM+k·MN≥k．

构造法的合理使用往往能使复杂的问题简单化，使“一筹莫展”的问题“柳暗花明”．构造法的最大难点是学生不易想到如何进行合理的构造，因此本题考查的是学生的直观想象能力和数学运算能力，不但要求能理解知识，还要能迁移知识，更能创造知识．本题的难度系数为0．35，大数据统计和预估相吻合．

3．3 命制说明

本题是以几何动态方法命制的求最小值问题．创作的灵感源于在研究正方体线面结构关系时，一个偶然的机会发现可以构造形如求PM+k·MN类型的最小值问题．平面几何题目通过构造立体图形来做是这道题目的精妙之处．画一个假设图形，假设它的各个部分都满足题目条件，也许是迈出解题的重要一步［2］．根据所求的特征，构造出相应的几何体，使等式中的一些数量关系显现在几何体中，有时能使我们豁然开朗，茅塞顿开;只需借助几何体的性质，即可得到简捷的证明途径．试题呈现方式简洁新颖，内涵丰富．立体几何平面化是解立体几何题目的重要方法，而平面几何蕴含于立体几何中显示出命题者的高明命制技术，但在学生的具体做题中又有不同途径可以解决它，体现了以生为本的命题情怀．因为有诸多优点，所以本题被选为浙江省宁波市2017学年第一学期期末考试的填空压轴题．

创新试题的命制过程犹如加工一件精致的艺术品．一般来说，题目命制应该是有法可循的，要真正命制一道好题，需要有创新精神，大胆猜想，小心求证，经历反复斟酌、艰难探究、多次修改、科学验证等过程才能定稿．命题成型时，既要关注试题整体呈现的形式，又要关注细节是否有瑕疵．正如罗增儒教授在《数学解题学引论》一书中所说:“命制数学题需要深厚的知识功底、良好的思维素质和熟练的编题技巧．有时候，创造一个问题比解决一个问题更困难．”这就要求命题教师要学会在平时的解题中欣赏试题，学会用数学的眼光观察世界，不断总结命制方法，数学地思考问题，加强解题研究，学会用精湛的命题艺术去呈现数学的美妙．