解题细节促能力 课堂教学育素养*

●唐俊涛 (吴县中学，江苏苏州 215151)

解题是中学数学教学过程的首要任务，在平日的教学课堂上，教师非常重视解题．但在实际讲解过程中，教师却往往忽视了对题目的分析、探索过程，实行的是灌输式、结论式教学，解题思路的选择一猜就灵、一选就准、一证就对，另外选择练习往往采用的是题海战术，指望学生通过大量练习，形成条件反射，机械式模仿教师的解题过程．缺少“实战”经验，使得学生在练习、考试中一旦遇到“面生”的习题，解题思维就会受到阻碍，联想转化能力得不到提高，致使花在数学上的时间很多，但是收效甚微，分数得不到提高．

教师在课堂讲题时常常是事先看过解答过程，并做好了非常充分的准备，因此课堂上教师都能把“思路”讲得清清楚楚，似乎每一步都是非常顺畅，都是自然而然的，学生也听得“津津有味”，似乎理解得很透彻，但是实际在自己解题的时候却并非如此顺畅．那么如何进行解题教学呢?笔者通过几个具体的方面进行分析，希望得到各位专家同仁的指导．

1 揭露解题中错误的本质

学生犯错的原因是五花八门的，有时题目做错了，及时订正，等到下次遇到了还是错．这种一错再错现象的背后隐藏了什么原因呢?教师解决错题的模式，往往是指出学生出错的地方，然后给出统一正确的解法，再通过一系列的类似问题进行强化．这样的操作似乎解决了学生当前的问题，却忽视了问题的背后，学生只知道“错在哪里”，但不明白“为什么会犯错”，等隔了一段时间后，到下次再做类似的题目时，仍旧犯错，这种纠错解题教学并不能真正解决该问题．

例11)若函数f(x)=log2(x2+2ax－a)的定义域为R，则实数a的范围是______;

2)若函数f(x)=log2(x2+2ax－a)的值域为R，则实数a的范围是______．

学生在解答这类题型时常常将“值域为R、定义域为R”弄混淆，何时用Δ＜0总是分不清，为什么值域为R时要用Δ≥0?表面上看，学生好像混淆了定义域与值域，而其实是教师平时讲解习题时“重结果，轻过程”导致的．在评讲过程中教师只是告知学生“应该这么做”，但是“为何要这么做”，却没有深入讲清、讲透，导致学生可能通过短时记忆强行记住了，时间一长再次犯错也就在所难免了．

怎样讲解能避免这样的问题呢?笔者认为可让学生先暴露他的错误，教师在点评时可以告诉学生，对数函数的值域为R，要确保对数的真数能取遍所有的正数，这时就要求真数上的二次函数的最小值小于等于0，即Δ≥0，学生所纠结的是“对数中要保证真数大于0，可是现在真数的最小值反而比0小”．其实这样的纠结大可不必，教师在评讲时可以消除学生的顾虑，虽然此时二次函数的最小值小于等于0，但是其作为真数还是要保证大于0，两者需要取交集，这样就能够保证对数真数取遍了所有的正数，该函数的值域就是R了．而定义域为R则是要确保每一个x对应的真数都要大于0，即真数的最小值大于0，亦即真数上的二次函数x2+2ax－a＞0恒成立，需要Δ＜0．

问题暴露不可怕，只要教师讲清问题本质，让学生明白发生错误的原因，才能从根源上消除再次犯错的隐患，因此平时解题教学中需要多多暴露典型错误、关注典型错误，不能“避重就轻”，针对错误，讲清原理，深挖问题背后的概念，让学生不再混淆概念，弄清问题的本质．

2 让学生体会解题受阻点

华罗庚先生说过:“不要只给学生看做好的饭，更要让学生看到做饭的过程．”学生解题时探求解题途径、思路不可能一帆风顺，往往会受到很多阻碍和挫折，达不到最终的目标．解题受阻是解题过程中最常见的问题之一，现实教学中，教师为了节省教学时间，常常直接告知学生结论或解题思路，表面上节省了教学时间，学生也可能通过短时记忆掌握了方法，但是这样的记忆是不会长久的．这样的解题教学没有展示学生解题受阻后如何处理的想法及思维过程，时间一长，再次遇到类似的问题时，原来的阻碍点仍旧会变成学生难以突破的难点．要摆脱这样的障碍，就要求教师在讲解过程中站在学生的角度去充分考虑思维上的阻碍点，帮助学生寻求受阻后转化的策略及方法．

例2已知函数 f(x)=ex+m－x3，g(x)=ln(x+1)+2．求证:当 m≥1时，f(x)＞g(x)－x3．

本题常规的解题思路是:f(x)＞g(x)－x3等价转化为

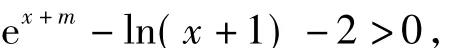
通过构造函数

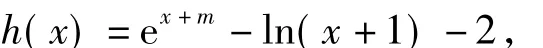
试图利用求导的方式求出h(x)的最小值，使其大于0．但是h'(x)中含有参数m不能直接求出导数的极值点，此时问题的障碍点显现．其实通过分析容易发现产生障碍的原因就在参数m上，由m≥1，可知

不等式ex+m－ln(x+1)－2＞0再次转化为

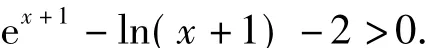
到此障碍点就得到了突破，下面的解题思路就比较清晰了．可以直接研究函数y=ex+1－ln(x+1)－2的最小值，也可借助于切线不等式(如ex≥x+1(当x=0时取等号)，lnx≤x－1(当 x=1时取等号)，sinx≤x(当 x=0 时取等号))，可知

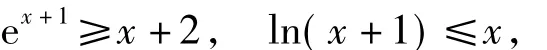
将原不等式变形为

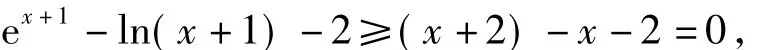
即原不等式成立．

教师平时在授课或者答疑过程中可以采取“现推现想”的做法，将问题的受阻点展现出来，并展示受阻时应该如何思考、如何突破思维障碍，让学生从教师的思维过程中学到突破困境的思考过程，让学生参与整个解题的过程，这样的记忆才是最深刻的．解题的主体是学生，教师在教学中应该突出学生主体的地位，让学生去探索、思考，从而提高自身的解题能力．

3 解题不再是满堂喝彩声

教师平时的课堂是精心准备的，每一个推理、每一个步骤都是经过再三思量的．因此在讲解后学生总感觉解法是一种必然的结果，当教师评讲完题目时总会发出阵阵赞叹声:“这样的解法真奇妙，这样的思路真是简洁，这样的技巧真是高明……”可是当学生自己去处理问题时却感觉无从下手，“只能像只无头苍蝇到处乱撞”，长此以往学生在感慨教师“厉害”的同时还会误以为自己是有多么笨，从而失去了学习的信心，适得其反．因此在平时的课堂中我们要少一点赞叹声，多一点质疑声:“我讲的解法学生能想到么?我讲的思路是学生常用的思路么?如果我是学生能想到这样的方法么?”多听听学生的想法，多让学生开口，教师只是引路人，引导学生去阅读题目、引导学生去思考问题、引导学生去调整解题方法，而不是代替他去解题．

课堂中教师也要尊重学生的思考结果，鼓励学生去思考，无论学生思考的结果是否成熟、是否可行，不能简单地肯定与否定．当学生遇到难题不会解决时，教师需要鼓励学生大胆去探索、去尝试，在这样的长期训练下学生独立解决问题的能力、思考分析问题的能力必将得到进一步的提升．

例3若实数x，y满足则 x的取值范围______．

(2013年全国高中数学联赛试题第7题)

本题的解决方案是将两个根式进行换元，利用数形结合将问题转化为常见的点与圆的最值问题．但是在教学过程中如果直接告知学生用换元法解题，就让学生失去了探索问题、思考问题的思维过程．教师可以通过问题的形式帮助学生找到解决该题的突破口．本题的难点是已知等式中的两个根式，学生往往第一反应是进行平方将根式消除．但通过实际操作会发现平方后的等式比原等式要繁琐，那么如何不进行平方，又可以将根式处理掉呢?学生自然联想到换元法，一次换元并不能解决问题，通过两次换元就能将问题解决．

4 转化问题的视角

解题时若遇到了陌生的、情境新颖的、平时没有接触过的问题，有时想不出解题思路怎么办?这时联想转化很重要，通过联想类比等方式将原本陌生的问题转化为学生熟悉的、已经解决过的问题，另辟蹊径让学生找到解决此类问题的思路途径．教师在这个过程中要积极引导学生去尝试、探索，从不同的视角(函数视角、不等式视角、三角视角、方程视角等等)去观察问题，不能受限于问题的表面，通过适当的铺垫让学生去尝试转化，从而使问题得到解决．

例4若实数x，y满足x2+y2+xy=1，求x+y的最大值．

本题是基本不等式应用的常见题型，处理方式往往是由已知条件x2+y2+xy=1，得

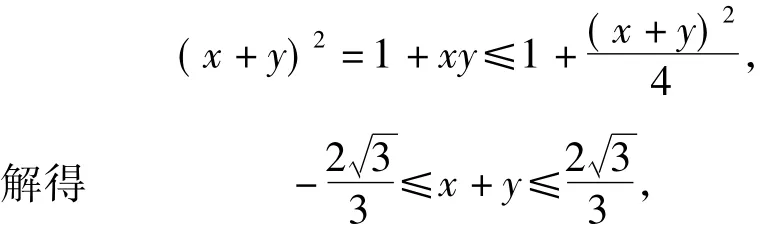
2)方程的角度:令 x+y=t，即 y=t－ x，代入x2+y2+xy=1，通过整理将其转化为关于x的二次方程x2－tx+t2－1=0．又因为方程有解，从而

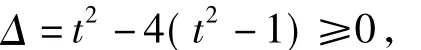
由此可见同样的题目从不同的视角来观察，可以得到不同的解题思路．长期这样的训练不仅可以拓宽学生的思维方式，对学生解题能力的提高也大有帮助，学生处理陌生问题时不会无所适从，自然会通过联想类比等手段找到解题的途径和方法．

5 学生独立参与解题

我们平时上课时所提及的“解题思路”有时是讲不清道不明的，只有当我们自己设身处地解题时才能体会到这一点．解题的每一个步骤不都是完完全全依靠逻辑，更多的是依靠对题目的感觉，如果解题过程越来越简洁，那么就离“胜利”就不远了，相反过程越来越复杂，那么就可能“此路不通”，需要重新考虑解题方案．

有思才有路，如果学生自己不动脑，只等着师生将答案告诉他，那么即使讲题人将过程说的非常清晰，到头来可能还是一头“雾水”，似懂非懂．这也就是很多学生反映的“课堂上教师讲的都能懂，但是当自己独立去完成相应习题时，却常常觉得寸步难行”．反之，如果学生在解题时已经认真做了思考，即使没有获得完整的解答，但只要得到简单的“提示”，被教师“点了一点”，也就能豁然开朗，独立地完成剩下的部分．因此教师在课堂上应多留一点时间让学生独立地去思考问题，探索多了自然就会摸索出一条属于自己的解题途径．

例5已知函数f(x(其中 a≠0)在(0，e］上的最大值为2，求a的值．

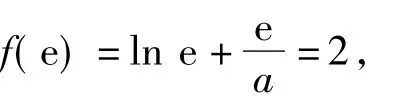
或者

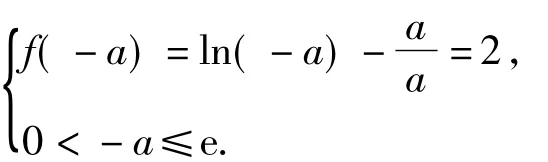
综上可得:a=e．

教学过程中要大胆地放开手，采用探究式的教学方式，让学生自主完成探索，让学生真正地去体会解决问题的喜悦，这样的解题印象才是最深刻、最牢固的．把探索问题的机会放手留给学生，和学生一起面对面处理问题，耐心地等待学生去探索和发现解决问题的途径，这样的课堂才是符合新课程标准的，才有利于提高学生的解题能力．

6 适当的题海有利于数感

适当的“题海”训练也是很有必要的，通过做题能培养出良好的数学感觉．我们常说的学霸无非可能就是比普通的学生多刷了一些题，题刷多了，自然就会有两把刷子了．可是学生经常反映:“做了很多的题目，解题能力为何并没有提升?”一部分原因是没有打好基础，忽视某些细节，使人“绊倒、摔跤”的往往是那些不起眼的小石子;还有一部分是没有做好总结，做完一道有难度的题目，一定要回顾一遍，弄清:解本题需要哪些步骤，哪些必须、哪些多余、哪些关键、哪些易得，有无更好的方法，总结是提高解题能力的一个重要环节［1］．

例61)已知数列{an}，a1=1 且 an=2an－1+2，则数列{an}的通项公式是______;

2)已知数列{an}，a1=1 且 an=2an－1+2n，则数列{an}的通项公式是______;

3)已知数列{an}，a1=1 且 an=3an－1+2n，则数列{an}的通项公式是______．

这组题型结构类似，都是通过构造新的数列来求通项公式．在第1)小题中an+2=2(an－1+2)，可得{an+2}是首项为3、公比为2的等比数列，即

an=3·2n－1－2．教师也可以引导学生归纳总结出该类题目的通法:若 an=pan－1+q，则数列{an+r}(其中 r为常数)为等比数列．

第2)小题的处理学生会参照第1)小题的解答，得

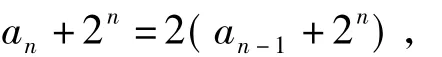
但是这样就犯了一个典型错误:若设bnn=ann+2n，

则

构造an+2n=2(an－1+2n)这样的形式是有问题的．可以两边同时除以2n，得

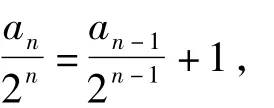
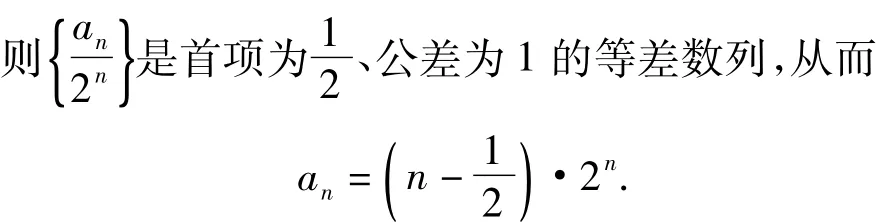
由此可以顺水推舟得到第3)小题的解答，将等式 an=3an－1+2n两边同除以 2n，得

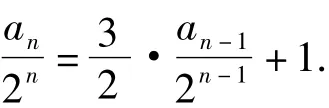
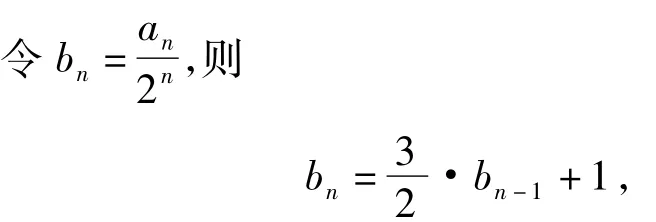
这样就可以转化为第1)小题的解题思路．由此我们可以得到an=pan－1+qn题型的解题思路了．

通过这样的类似题组训练，教师不仅可以帮助学生找到解题错误产生的原因，领悟纠正错误的方法，进而提炼出解题的通性通法．

教学过程中教师还可以继续将题目进行“发散”:若条件是 an=2an－1+2n －1，an=2an－1+2n2，又应该如何探究处理呢?教学过程中教师要引导学生学、思结合，发挥创造性，努力产生“好想法”，同时也要注意适时的总结．提高解题能力的捷径就是反思与总结．

学生解题不可能每次都是“一蹴而就”，有时需要尝试—调整—再尝试—再调整……如此反复，最后还需要进行反思和总结．在此过程中，教师需要给学生信心，鼓励他们独立思考，适当作出引导，让学生一步步逼近目标，这样不仅可以让学生的思维、解题能力得到提高，而且相应的意志品质也可以得到提升与磨练．正所谓:“解题细节促能力，课堂教学育素养．”