铯原子喷泉钟空间均匀C场的研究

施俊如,王心亮,阮军,管勇,3,白杨,刘浩,3,杨帆,3,刘丹丹,3,张辉,张首刚

(1.中国科学院 国家授时中心,西安 710600；2.中国科学院 时间频率基准重点实验室,西安 710600；3.中国科学院大学,北京 100049)

0 引言

铯原子喷泉钟是复现“秒”定义的频率基准装置。在铯原子喷泉钟中的激励腔和自由飞行区加有竖直方向100 nT左右的均匀静磁场,称为C场。C场是铯原子喷泉钟物理系统的重要组成部分,其主要作用有两个：①使原子的基态能级发生塞曼分裂；②为原子跃迁提供一定的空间取向,使|F=3,mF=0>↔|F′=4,mF=0>能级之间的跃迁得以实现。铯原子喷泉钟里的C场设计应满足两个要求：①原子飞行路径上的磁场起伏尽量小；②磁场随时间变化尽量小。其中C场均匀度是由长直螺线管产生的磁场、磁屏蔽剩磁和残余地磁场决定,C场的空间均匀度直接影响二阶塞曼频移的测量不确定度。

笔者首先理论研究了二阶塞曼频移及由C场空间均匀度引起的频率不确定度。实验研究了对磁屏蔽的拆分退磁法和整体退磁法,且获得了高均匀度的C场。最后获得了二阶塞曼频移及由C场空间均匀度引起的二阶塞曼频移不确定度。

1 二阶塞曼频移的理论研究

二阶塞曼频移是指在C场作用下,铯原子能级发生移动,引起钟跃迁频率发生变化,通常用相对值表示[1-2]。

(1)

式(1)中,v0表示无外场干扰下铯原子基态塞曼子能级|F=3,mF=0>到|F′=4,mF=0>跃迁的定义频率,为v0≡9 192 631 770 Hz。相对磁场强度xB=μBB(gJ-gI)/hv0,铯原子电子和核的朗德因子gJ=2.003,gI=-0.40×10-3,玻尔磁子μB=9.27×10-24J/T,普朗克常数h=6.62×10-34J·s。

因此铯原子的0-0和1-1跃迁,对应的频率为(忽略高阶项)

(2)

(3)

由式(2)进一步得到了二阶塞曼频移表达式

(4)

式(4)中〈〉表示对原子飞行路径上的时间加权平均。1-1跃迁相对于钟跃迁定义频率差为

(5)

因此二阶塞曼频移可以用Δv1-1表示为

(6)

实际上原子飞行路径上的磁场是非均匀的,每一点的磁场值等于平均磁场加一个偏差[4]:

Bi=〈B〉+σi,

(7)

〈B2〉=〈B〉2+σ2,

(8)

因此由C场的空间不均匀引起的二阶塞曼频移不确定度为

(9)

实际上,由于原子上抛和自由下落过程中经过每一点的时间不同,所以σ是原子飞行路径上经时间加权后磁场的标准差。具体计算方法如图1所示[5]。

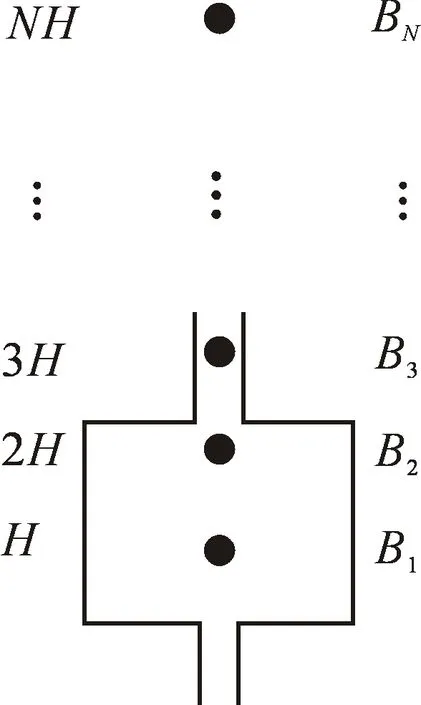
图1 原子飞行路径上磁场的时间加权

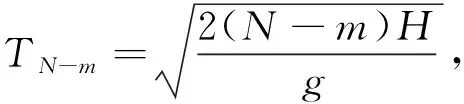
所以经时间加权后的磁场平均值为

(10)

标准差为

(11)

将式(10)和(11)代入式(6)和(9),即可求出二阶塞曼频移和由C场空间均匀度引起的二阶塞曼频移不确定度。

2 磁屏蔽性能研究

为了构建100 nT左右、且空间均匀度较高的C场,实验上我们将C场组件放置在具有高磁导率的磁屏蔽装置(JIS C 2531 PC 软磁合金材料)中,以此来屏蔽外界杂散磁场的干扰。磁屏蔽装置如图2所示。

C场由3部分组成：①长直螺线管产生的磁场；②磁屏蔽外的空间杂散场经磁屏蔽后的磁场；③磁屏蔽装置的剩磁。其中第3项是影响C场空间均匀度的最主要因素,因此在磁屏蔽初次组装完成后对其剩磁进行了测量。通过用磁强计测量得到磁屏蔽剩磁有50～200 nT,且在50 cm范围内起伏约有60 nT。这是由于磁屏蔽在运输途中磕碰和组装过程中的应力所致,因此在磁屏蔽组装完成后对其进行了整体退磁。即将单根导线穿过磁屏蔽和真空管道之间,通入10匝20A/匝的工频电流进行退磁。以磁屏蔽中心为0点,竖直向上为正方向,磁屏蔽整体退磁后,从磁屏蔽最下端竖直向上移动磁强计探头(分辨率为0.1 nT)测量剩磁,每移动0.5 cm记录一个数据,测量结果如图3所示。可以看出此时剩磁在47 cm范围内起伏小于1 nT,且由于交流退磁过程中会屏蔽掉一部分磁场,使得磁屏蔽下端较中部退磁作用变小,相对NTSC-F1磁屏蔽性能也有了明显的提高[6]。

图2 磁屏蔽装置结构 图3 磁屏蔽整体退磁后剩磁分布

3 C场测量与二阶塞曼频移评定

基于上面均匀度良好的背景磁场,我们将特定通电长直螺线管放置于磁屏蔽中心来构建C场。通电长直螺线管结构设计如图4所示。漆包线密绕在具有良好电绝缘特性的聚四氟乙烯树脂制成的C场结构桶上,该桶高L=730 mm,半径R=130 mm,线圈匝数密度n=280 匝/m。

图4 长直螺线管结构

通电长直螺线管产生的C场分布满足比奥—萨法尔定律[7],因此在自由空间,以螺线管中心为原点O,中心轴线向上为x轴正方向(与上述实验所设坐标系对应),轴上任一点P(x)的磁场大小为[8]

(12)

式(12)中I是通入长直螺线管的电流,真空磁导率μ0=4π×10 T·m/A。

将上述各参数代入式(12),计算可知若要产生100 nT左右的磁场,长直螺线管需要通入约300 μA的电流。因此在这里设置电流I=297 μA,代入式(12)可得该长直螺线管中心轴向磁场分布情况,如图5中实线所示。同时,实验上给长直螺线管通入相同电流,用磁强计对磁屏蔽内的C场进行了测量,步进为1 cm,测量结果减去剩磁即是长直螺线管在磁屏蔽内产生的磁场,如图5中点线所示。可以看出实验值相对计算值大,且均匀度好,这是由于式(12)是长直螺线管在自由空间产生的磁场,而在磁屏蔽内的长直螺线管轴线上磁场会由于磁屏蔽端盖的影响而产生镜像效应[9],因此磁场强度变大、均匀区长度也会得到延伸。但是由于端盖的开孔和接缝的影响,使得磁屏蔽内长直螺线管轴线上磁场计算变得困难[10]。

图5 磁屏蔽筒内长直螺线管轴线上磁场

同时也得到了如图6所示的C场强度分布情况,可以看出在没有补偿线圈的情况下,磁屏蔽内竖直方向48 cm范围内C场起伏小于1.5 nT。相对NTSC-F1在添加3个补偿线圈情况下的C场均匀度( 48 cm @1.7 nT)[11]有了明显的改善。

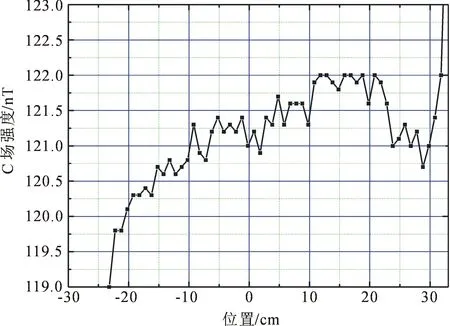
图6 C场强度分布

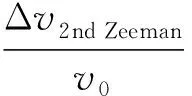
(13)

(14)

4 总结

本文依据铯原子喷泉钟弱均匀稳定C场的设计要求,通过整体退磁法获得了均匀度良好的C场。并通过对现有磁场的推理计算,获得了NTSC-F2的二阶塞曼频移为68.7×10-15,由C场空间均匀度引起的二阶塞曼频移不确定度为6.05×10-19。该项是二阶塞曼频移不确定度的其中一项,另一项是由C场随时间变化引起的二阶塞曼频移不确定度,且该因素是引起二阶塞曼频移不确定度的最主要一项[12]。因此,C场空间均匀度的提高不仅使对应的不确定度相对NTSC-F1提高了一个量级,更重要的是该设计避免了由于添加补偿线圈,而引入的补偿电流不稳定带来的C场随时间的扰动,因而进一步提高了二阶塞曼频移不确定度。下一步将通过设计高稳定C场电流源来进一步降低由C场随时间扰动引起的二阶塞曼频移不确定度。