基于SFT方法的MBOC信号快速捕获性能分析
黄夏妹,王雪,陈校非,郭瑶
(1.中国科学院 国家授时中心,西安 710600;2.中国科学院 精密导航定位与定时技术重点实验室,西安 710600;3.中国科学院大学 物理科学学院,北京 101048;4.中国科学院大学 电子电气与通信工程学院,北京 101048)
0 引言
近年来,各国卫星导航系统的发展十分迅速,已经成为信息时代国家重要的基础设施之一[1]。信号体制是卫星导航系统的关键技术之一,近年来GPS L1频点的信号体制经历了从BPSK(binary phase shift keying)到BOC(binary offset carrier)再到MBOC(multiplexed BOC)的发展[2-3]。新的信号体制为卫星导航信号的接收带来了巨大的挑战,尤其是MBOC信号在测距码周期上的变化;QMBOC(quadrature multiplexed BOC)和TMBOC(time multiplexed BOC)信号的测距码周期是10 ms,CBOC(composite BOC)的测距码周期是4 ms,而传统的BPSK信号测距码周期是1 ms。与传统BPSK信号相比,在使用相同接收方法的前提下,导致MBOC信号捕获时运算量的成倍增长。因此有关MBOC的信号捕获研究中多围绕着如何降低运算复杂度展开。文献[4]介绍了一种优化GPS(global positioning system)系统的L1 CA码信号捕获法,该方法通过信号压缩来降低CA码捕获运算复杂度,进而提高捕获性能。在文献[5]中将稀疏傅里叶变换应用于GPS L1CA码捕获,这种方法通过降采样减少FFT(fast Fourier transform)的点数,提高捕获效率,优化捕获性能。由于TMBOC信号码周期与GPS L1 CA码周期不一样,并且TMBOC信号在一个码周期内发生导航电文跳变的概率和GPS L1CA码不一样,所以该方法不能直接用于TMBOC信号捕获。文献[6]将改进的稀疏傅里叶变换(sparse Fourier transform,SFT)应用于QZSS(the Quasi-Zenith satellite system)系统中的TMBOC信号捕获,研究表明,该方法有效降低了捕获时的运算复杂度,提高了捕获效率。本文将SFT方法分别应用于QMBOC,TMBOC和CBOC信号捕获,并将该方法与传统的整周期FFT捕获方法进行了对比,对比3种MBOC信号的捕获的性能。
本文主要分4部分,首先介绍MBOC信号实现方式及其相关特性,其次介绍稀疏傅里叶变换的原理及快速捕获的实现过程、再从运算复杂度和检测概率分析了MBOC快速捕获性能,最后采用实测数据进行分析,所得真实值与理论值基本吻合。
1 MBOC信号实现方式及其相关特性
MBOC调制信号的定义是在频域上的,它时域实现方式主要有3种,即北斗B1C的QMBOC,GPS L1C的TMBOC以及Galileo E1B/C的CBOC[7]。
北斗B1C信号的数据分量占总功率的25%[8],采用BOC(1,1)调制;导频分量占总功率的75%,采用QMBOC(6,1,4/33)调制。QMBOC中的两个子载波BOC(1,1)和BOC(6,1)分别在两个相互正交相位上。QMBOC(6,1,4/33)的基带形式[9]可由式(1)表示:
(1)
式(1)中,gBOC(1,1)(t)表示BOC(1,1)子载波,gBOC(6,1)(t)表示BOC(6,1)子载波,式中的“±”分别对应正相QMBOC和反相QMBOC。
采用BOC(1,1)调制,GPS L1C信号的数据分量占总功率的25%[9];采用TMBOC调制,导频分量占总功率的75%。TMBOC中的两个子载波BOC(1,1)和BOC(6,1)采用时分复用的方式在时域中有规律地复合在一起,TMBOC(6,1,4/33)的基带形式可定义为:
(2)
式(2)中,dk是导航电文,Ck是伪码,其周期为10 ms,gk是子载波,k值决定此时隙采用BOC(1,1)还是BOC(6,1)子载波。
Galileo E1信号的导频和数据分量各占总功率的一半[10]。CBOC可分为正相和反相,即CBOC(6,1,1/11,“+”)和CBOC(6,1,1/11,“-”),分别调制在数据和导频两个通道上,记作CBOC+和CBOC-。CBOC+和CBOC-的子载波可用公式(3)来表示:
(3)
式(3)中,gCBOC+表示正相CBOC子载波,gCBOC-为反相CBOC子载波。图1至图4依次是QMBOC,TMBOC和CBOC的时域波形。

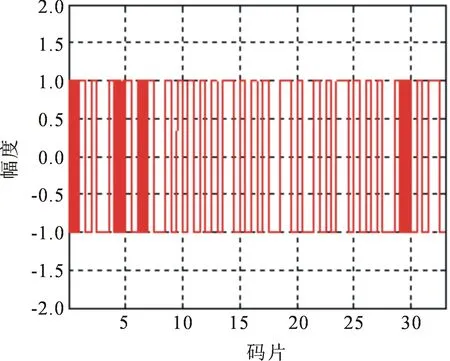
图1 QMBOC时域波形
图2 TMBOC时域波形
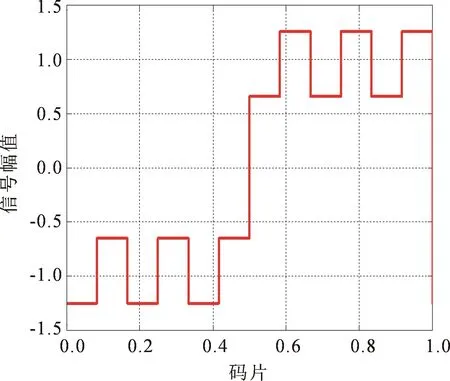
图3 CBOC+时域波形
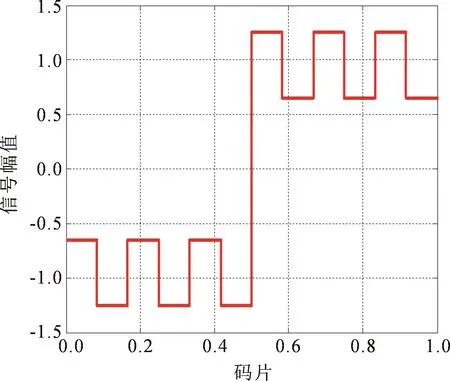
图4 CBOC-时域波形
根据前面分析以及图1至图4可知QMBOC,TMBOC和CBOC信号实现方式不同导致了3者的时域波形各不相同。通过对信号的时域波形进行自相关运算可以得到该信号的自相关函数,MBOC信号自相关函数如图5所示。由图5可知QMBOC,TMBOC和CBOC信号的自相关函数都是分段线性且有多个相关峰,这造成了MBOC信号捕获和跟踪时存在模糊度;从图5中也可以看出相比于BPSK(1)信号3种MBOC的主峰都很窄且尖锐,这说明了QMBOC,TMBOC和CBOC调制信号具有跟踪精度高、抗干扰强等优点。
从图6的MBOC(6,1,1/11)理论功率谱可知,相比于BOC(1,1)调制信号,由于MBOC调制信号中存在BOC(6,1)分量,导致其功率谱中增加了高频分量,这样可以提高抗干扰的能力,提高接收机的性能。

图5 BPSK(1),BOC(6,1)与MBOC(6,1,1/11)自相关函数

图6 MBOC(6,1,1/11)理论功率谱
2 稀疏傅里叶变换及快速捕获实现
稀疏傅里叶变换是由MIT(Massachusetts Institute of Technology)的4位研究人员提出的一种改进的离散信号傅里叶变换[3](discrete Fourier transform,DFT)算法。该算法巧妙利用信号在频域的稀疏特性,通过对信号在频域上的抽样来降低信号的FFT点数,进而有效降低信号处理的运算复杂度。本文将稀疏傅里叶变换应用在MBOC信号快速捕获中,并将其与传统的方法对比。
假设有限长为N的序列x(n)的DFT为X(k),则根据离散傅里叶变换,x(n)和X(k)存在以下关系[8]:
(4)
(5)
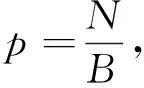
x′(n)=x(n)+x(n+B)。
(6)
相应地在频域上就相当于对原始信号进行抽样[5],令X′(f)为抽样后的频域信号,则f=0,1,…,B-1,该过程可以由以下公式表示:X′(f)=X(pf),其中p为抽样系数,在本文的快速捕获中降采样系数P=2。
快速捕获实现的过程如图7所示。在接收模块,本地先读取整周期信号,QMBOC和TMBOC为10 ms,CBOC为4 ms;然后按照每段1 ms对读入的信号进行分段,对每段信号进行降采样,即稀疏傅里叶变换处理;再分别与本地产生的伪码与载波相乘,实现对信号的伪码与载波剥离,得到快速捕获的捕获判决量;最后将判决量与设定的捕获门限相比,如果判决量小于门限值,那么跳至所读入信号的下1 ms继续搜索,如此循环,直至捕获所得判决量大于门限值,在该判决量中寻找最大相关值所对应的载波频率和码相位,即为快速捕获的结果。图7中IFFT为快速傅里叶逆变换。
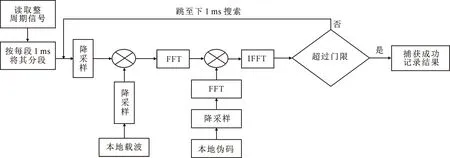
图7 SFT快速捕获实现过程
3 快速捕获性能分析
捕获的性能包含单次检测概率、虚警概率和运算复杂度等,本节的快速捕获性能只分析运算复杂度和单次检测概率。
3.1 运算复杂度
运算复杂度是捕获性能的重要指标之一,该指标直接关系到捕获过程所消耗的时间。本试验所采用的数据参数设置如下:采样率为250 MHz,中频为62.5 MHz,令其读取信号长度为M,所读取的信号采样后的点数为N,搜索步径为Δw,多普勒搜索频点数为f。在快速捕获中,搜索步径都是Δw=50 Hz,对于TMBOC和CBOC,其多普勒搜索范围都是±5 kHz,多普勒搜索频点数都是f=201;而对于QMBOC信号,考虑卫星动态和射频前端本振偏差,其多普勒搜索范围设置为±10 kHz,其多普勒搜索频点数f=401。
对于QMBOC和TMBOC信号,预检积分时间为M=10 ms,N为2 500 000点;采用快速捕获方法,经过稀疏傅里叶变换后N为125 000点。对于CBOC信号,预检积分时间为M=4 ms,N为1 000 000点;采用快速捕获方法,经过数据分段和稀疏傅里叶变换后N为125 000点。这3种MBOC信号的快速捕获方法在FFT时所消耗的运算量时实乘运算都是NlogN,在IFFT(inverse fast Fourier transform)时所消耗的实乘运算也是NlogN[5],再加上频率井搜索时所消费的实乘运算,那么快速捕获算法总的运算量是t1=fN+2fNlogN[5]。
前面所分析的快速运算量只包含对读入每1 ms信号的快速捕获过程,如果得到的判决量小于捕获门限,那么将进入下1 ms继续进行快速捕获处理,这时候就需要重新计算快速捕获的运算量。对于TMBOC和QMBOC信号,测距码周期都是10 ms;那么读入一段10 ms的数据,这段数据的每1 ms内跳变的概率都是1/2。信号的码相位在读入的整周期信号中服从均匀分布,因此整周期内每1 ms的跳变概率是一样的,都是1/10。假设读入整周期信号中跳变的位置为第i毫秒,那么跳变耗时t(i)和i之间的关系可用公式(7)表示:
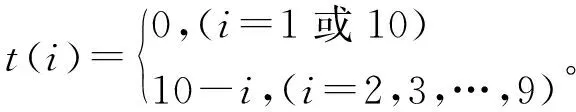
(7)
根据均匀分布可知:
(8)
根据式(7)和式(8)跳变的平均耗时为
(9)
同理可得对于CBOC跳变平均耗时为
(10)
则快速捕获所需平均运算量为
(11)
(12)
将所采用的相关参数设置代入式(11)和式(12),可得表1。

表1 整周期捕获与快速捕获运算复杂度对比
通过表1可知,相比于整周期捕获,快速捕获在运算复杂度上:TMBOC能够降低95.98%,CBOC能够降低85.93%,QMBOC能够降低95.85%,说明采用稀疏傅里叶变换实现快速捕获能够有效降低MBOC捕获的运算复杂度。
3.2 单次检测概率
虚警概率pfa和检测概率pd是评判捕获性能好坏的两个重要指标[10]。H1假设条件有信号,H0假设条件为无信号,那么H1条件下判决通过门限Thr的概率称为检测概率,相应地将H0情况下判决变量通过门限Thr的概率为虚警概率,在理论仿真中往往通过计算理想情况下载噪比与检测概率的关系来衡量不同捕获算法的性能。对于MBOC信号的快速捕获,其检测概率可以由公式(13)来表示[5]:
(13)
式(13)中:Q(a,b)表示马库姆Q函数;λ表示检测量,且λ=nAR(τ)ρ,其中A表示信号幅度,n表示未降采样之前的采样点数,R(τ)表示本地码与读入信号相乘后得到的自相关函数,ρ=sinc2(πΔfnt),Δf为输入信号和本地信号的频差;Thr表示捕获的检测门限,计算公式如下:
(14)
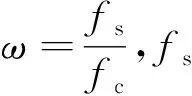
(15)
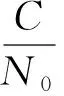
(16)
式(16)中,Bn为带宽。根据式(13)~(16)且将虚警概率Pfa设为10-5,将北斗B1C与GPS L1C整周期捕获记为方法1,Galileo E1整周期捕获记为方法2,将GNSS L1采用SFT实现快速捕获记为方法3,画出快速捕获与传统整周期捕获法的载噪比与检测概率关系,如图8所示。

图8 快速捕获检测性能分析
从图8可以看出,从检测概率来看,QMBOC和TMBOC整周期捕获性能最优,这是QMBOC和TMBOC的整周期积分时间是10 ms;CBOC传统整周期捕获次之,最差的是快速捕获法。在检测概率设置为0.95时,QMBOC和TMBOC整周期捕获的输入信号载噪比是33 dB-Hz,CBOC整周期捕获的输入信号载噪比是37 dB-Hz,MBOC快速捕获的输入载噪比是47 dB-Hz。这说明对于QMBOC和TMBOC,在捕获灵敏度上,与整周期捕获相比,采用快速捕获下降了14 dB;对于CBOC,与整周期捕获相比,采用快速捕获下降了10 dB。
4 快速捕获实测数据结果分析
本文使用的数据均由中国科学院国家授时中心昊平观测站的空间信号质量评估系统所采集。QMBOC数据采用的是北斗三号卫星导航系统B1C信号的卫星号PRN为19,TMBOC数据采用的是北斗试验卫星工程B1C信号PRN为3和CBOC数据采用的是Galileo系统E1信号PRN为18。捕获结果用捕获所得的最大相关峰和第二相关峰的比值,即峰峰比来衡量,第二相关峰是在最大相关峰错开两个码片后得到的,这保证了第二相关峰即为信号噪底的功率,其中采样率为250 MHz,采样点间隔为4 ns;以62.5 MHz为中心频点,搜索步长设置为50 Hz的频率步进。QMBOC,TMBOC和CBOC各采集数据5组,利用同一平台进行分别用QMBOC,MBOC整周期捕获,CBOC整周期捕获和本文的快速捕获法,得到的结果如表2,3,4,图9和10所示。

表2 QMBOC快速捕获结果分析(卫星号为19)
通过表2,3,4和图9,10可以看出采用快速捕获方法后:捕获的峰峰比QMBOC下降了14.4 dB,TMBOC下降了13.59 dB,CBOC下降了9.5 dB;这与理论分析所得QMBOC,TMBOC下降14 dB,CBOC下降10 dB基本吻合;捕获耗时减少QMBOC是28.8%,TMBOC是61%,CBOC是60.2%,这与理论计算所得快速捕获对运算复杂度的改善也基本吻合。
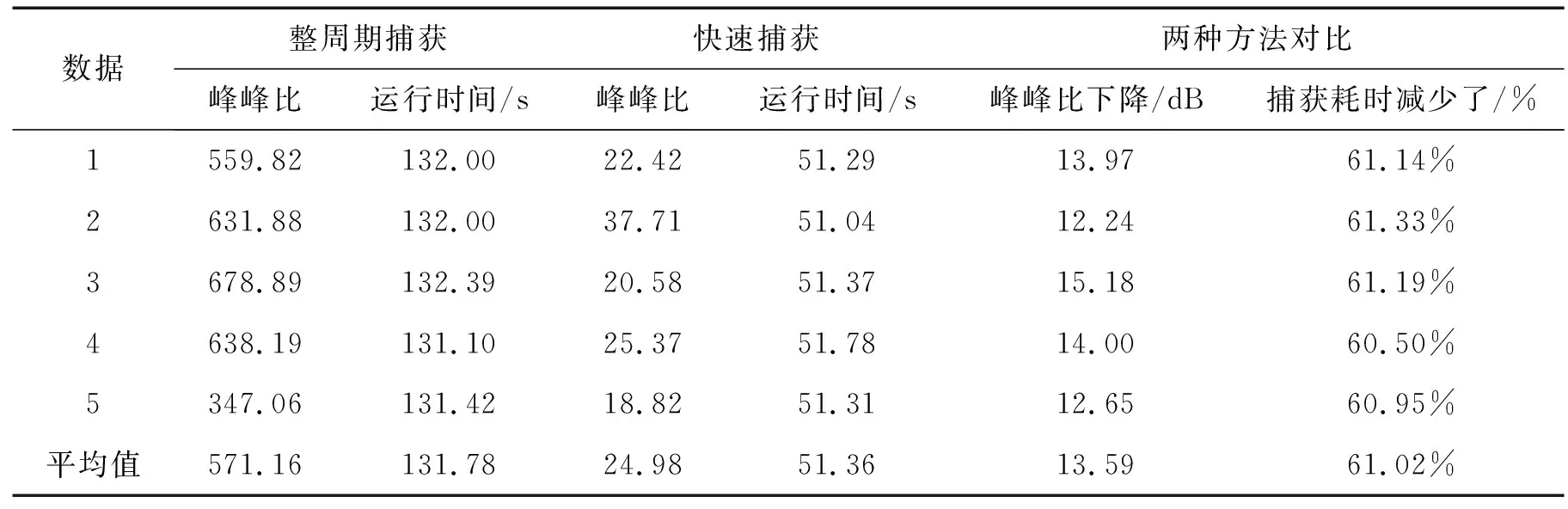
表3 TMBOC快速捕获结果分析(卫星号为3)

表4 CBOC快速捕获结果分析(卫星号为18)
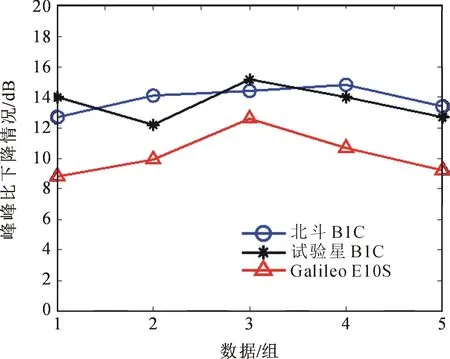
图9 MBOC快速捕获峰峰比下降统计结果

图10 MBOC快速捕获时间减少统计结果
5 结论
MBOC信号与传统BPSK-1信号相比,码周期较长,导致MBOC信号在捕获时增加了运算复杂度。本文根据MBOC信号码周期较长的特点,利用稀疏傅里叶变换进行降采样,实现对MBOC的快速捕获。相比传统的整周期FFT捕获,SFT快速捕获的运算量:TMBOC能够降低95.98%,CBOC能够降低85.93%,QMBOC能够降低95.85%。在对实际数据的处理中,SFT快速捕获能有效减小捕获耗时:QMBOC和TMBOC能够减少60%,CBOC能够减少28%。理论分析和实测数据结果都表明SFT快速捕获能够有效提高捕获效率。SFT快速捕获缺点是导致捕获灵敏度的恶化,但这可以通过延长积分时间来解决。通过前文的分析可知:整周期FFT捕获检测性能较优,但是计算量大,资源消耗较大,因此适用于硬件资源充足且对捕获速度没有要求的场景;SFT快速捕获的检测性能差,但计算量小,资源消耗较低,因此适用于硬件资源非常欠缺且对捕获速度有较高要求的场景。

