北斗定时接收机T-RAIM算法研究

徐荣,周同同,赵陆文,戴卫恒,田世伟

(1.陆军工程大学 通信工程学院,南京 210007;2.江苏指南针导航通信技术股份有限公司,南京 210007)

0 引言

随着科技的进步,现代国家基础设施的高效运转对时间信息的依赖性越来越强,要求时间服务精度更高的同时,对完好性和可用性要求也提出更高要求。文献[1]中国移动时间同步网技术体制标准要求GPS(Global Positioning System)定时接收机需要考虑卫星信号质量、安装的地理环境、电磁干扰及人为操作等因素的影响,即接收机需具备自主完好性监测能力。

利用接收机自主完好性监测(receiver autonomous integrity monitoring,RAIM)可以及早发现卫星故障并剔除,同时向用户发出告警,从而提高卫星导航授时服务的可靠性。文献[2]总结了常用的接收机自主完好性监测算法分为快照法和滤波法。快照法主要有伪距比较法、奇偶矢量法和最小二乘残差法,利用伪距冗余观测量进行故障检测和排除,无需外部设备支持,易实现,响应快；滤波法主要有卡尔曼滤波算法,利用历史观测数据增加冗余量,同时降低观测噪声,可以进行多星故障检测。

我国北斗导航系统可以提供高精度授时服务,不过目前还是区域导航系统,静止轨道卫星和倾斜同步轨道卫星数量占比较大,因此存在“南山效应”,某些地区受经纬度、地形以及城市峡谷影响在一定时间段内可见北斗卫星数量较少,这样冗余观测量也少。文献[3]指出快照法需要的卫星数量至少5颗以上才能进行故障检测,而且对卫星的几何分布也有一定要求,这样就不能满足北斗授时服务的可靠性要求。文献[4]指出基于卡尔曼滤波的RAIM算法对先验误差特性依赖性强,实际系统通常是非线性的,建模不准、外界干扰等都会带来残差,这些残差的存在容易造成故障误报。文献[5]针对定时接收机应用场景,测站本地位置已知,只有接收机钟差是未知量,提出了基于伪距残差平方和的T-RAIM算法,但其应用前提条件是单星故障,因此可用性受到一定影响。

笔者针对上述情况研究一种适用于北斗定时接收机的T-RAIM(timing-receiver autonomous integrity monitoring)算法,该方法利用恒温晶振的高稳特性,根据伪距残差平方和与累积的历史伪距残差及其标准差进行卫星故障检测,并通过不同场景验证算法性能。

1 定时接收机自主完好性监测算法

本文的T-RAIM算法主要是利用伪距残差平方和法进行当前时刻各观测值的横向比较,来检测和识别单星故障；利用历史伪距残差及其标准差法进行纵向对比,用于微小缓变以及多星故障检测,该算法适用于定时型接收机的静态应用场景。

1.1 基于伪距残差平方和与历史伪距残差及其标准差的T-RAIM算法模型

伪距残差向量[6]可用下式表示：

(1)

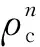
式(1)如果没有噪声和误差,伪距的实际测量值与其估计值是一致的,而在噪声和误差正常条件下,两值也比较小。当测量误差中含有较大的偏差时,伪距的估计值与实测值之间的差值就会变大。因此,可以利用伪距残差判断测量伪距中是否存在较大的偏差。但由于伪距残差向量不是一个标量值,故不能作为统计检测量,所以为了完全地保留误差信息,将各个分量的平方和(sum of the squares of range residual errors,SSE)作为统计检测量：

FSSE=bTb。

(2)

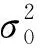
取伪距残差平方和为检测统计量,做以下两类假设：

①无故障假设H0：

(3)

②有故障假设H1：

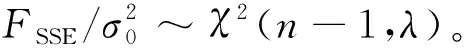
(4)

根据假设条件①,若无故障卫星时出现告警,则为虚警,给定虚警概率PFA,有下列等式[8]：

(5)

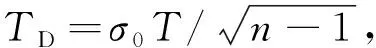
(6)

不过伪距残差平方和方法遇到多星故障和微小缓变故障时存在漏检概率,需要累积历史观测数据进行判别。在存储历史观测数据过程中,接收机钟差和卫星数是实时变化的,因此在判断周期内需要稳定的参考量作为判断依据。由于定时接收机配备的恒温晶振一般都具备短期稳定性高(秒稳在10-11～10-12左右)的特点,若每10 s调整1次钟差,其累计误差也不会超过0.1 ns,不调整本地晶振的钟差,使得伪距观测量基于近似相同时间基准,存储10 s的伪距残差及其标准差,卫星伪距观测量在此期间出现异常,故障卫星伪距残差会增大,可以根据此变化进行判别。当然钟差调整间隔可以根据实际故障检测需求和恒温晶振性能改变的。

伪距残差标准差的计算公式为

(7)

式(7)中,σ是伪距残差的标准差,n是卫星数,bi是第i颗卫星伪距残差。

1.2 故障检测和识别

图1中可以看出,为了更好解决冗余观测量少和微小缓变时的故障检测难题,改进T-RAIM算法在伪距残差平方和判别无故障后,继续利用存储的数据库进行故障检测,在时钟稳定后累计N(图中N=10)组历元的伪距残差及其标准差数据库进行判别,数据库更新采用“先入先出”的方式把最新无故障数据引入,剔出最旧数据。当前伪距残差标准差一旦超过数据库中最小门限,本地时钟暂不调整,由于本地时钟短期内足够稳定,故障卫星伪距残差会逐渐增大,从而在伪距残差平方和中鉴别出来,这种方式提高了此类故障检测概率。故障检测时两种特殊情况处理：①授时卫星为故障星,这会导致其他星的伪距残差值逐渐增大,起始时伪距残差的标准差增大,随后其他正常星的伪距残差会变差,标准差随之降低,与正常情况下的标准差值差异不明显,所以这种情况检测到进入守时后应立即予以处理；②可见卫星只有1～2颗时需扩大钟差调整间隔,加大累积卫星伪距残差变化数据,以此鉴别卫星故障。

2 仿真验证

设定仿真条件：PMD=1×10-4,PFA=1×10-5,σ0=16 ns,得到不同可见卫星数对应的检测门限和非中心参数如表1所示。

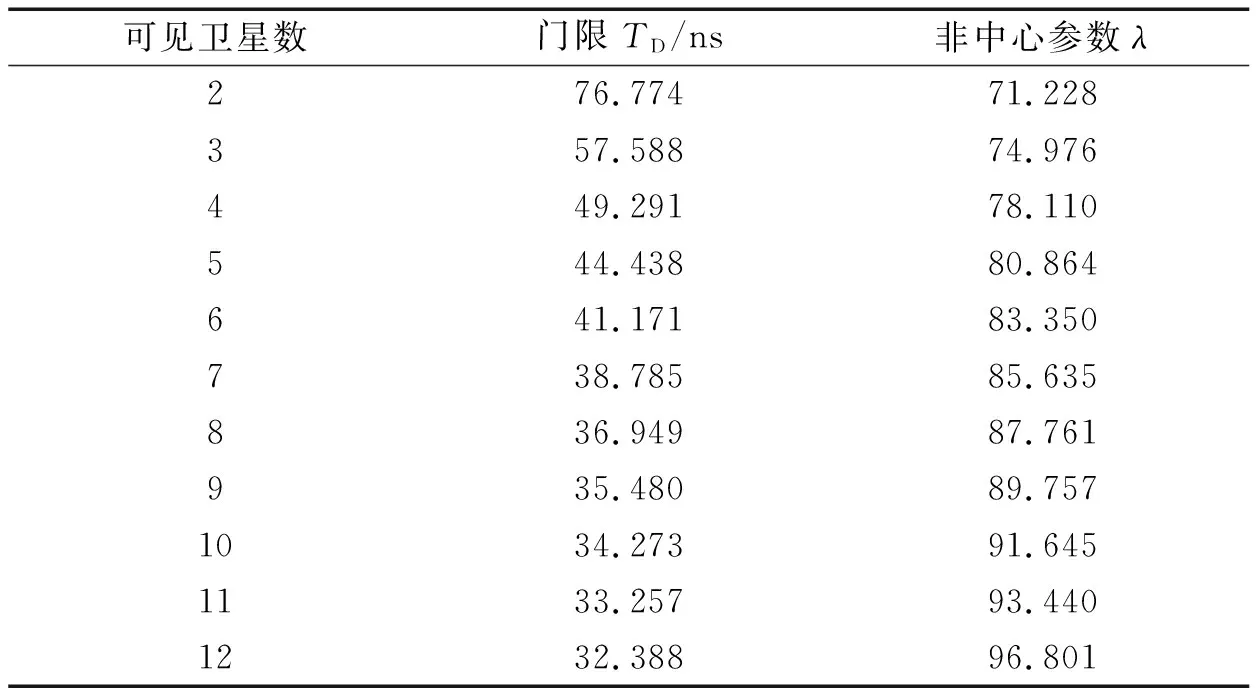
表1 不同可见星、非中心参数和故障判别门限(PFA=1×10-5)

选取不同仿真场景进行验证,基础数据来自江苏指南针导航通信股份有限公司的北斗定时接收机实测数据,数据历元间隔为1 s。

①阶跃式故障

此场景为实测结果(UTC时20170201T22:43:30/12:45:10),图2中8颗北斗卫星中一颗卫星在第75个历元发生阶跃故障(400 ns左右),由于检测统计量急剧增大超过检测门限36.9 ns,立即被识别剔除,伪距残差标准差也迅速恢复正常。

图2 阶跃故障检测和识别

②斜坡式故障

此场景为仿真数据,图3中起始阶段6颗北斗卫星伪距残差符合均值为15 ns,标准差为1 ns的正态分布,将其中一颗星在第300个历元起始加入每秒0.2 ns递增的粗差,在粗差增长的初始阶段,由于检测统计量没有超过门限,因此无法识别,但是伪距残差标准差在逐渐增大,因此本地时钟不调整,在粗差增长到检测门限49.291 ns时,即可识别剔除,伪距残差标准差也迅速恢复正常。相比传统方法,基于历史伪距残差标准差判别,无需对本地时钟建模,可用性更强。

③多星随机故障

此场景为实测数据上叠加测试数据,图4中8颗卫星中在历元第75～95个历元之间在2～3颗卫星伪距残差上叠加30～80 ns随机粗差,可以看出在识别剔除故障后,仍有伪距标准差比正常情况略大的情况,这是由于个别卫星的粗差虽然略大但整体伪距残差标准差仍在检测门限36.9 ns下,因此未被检出。

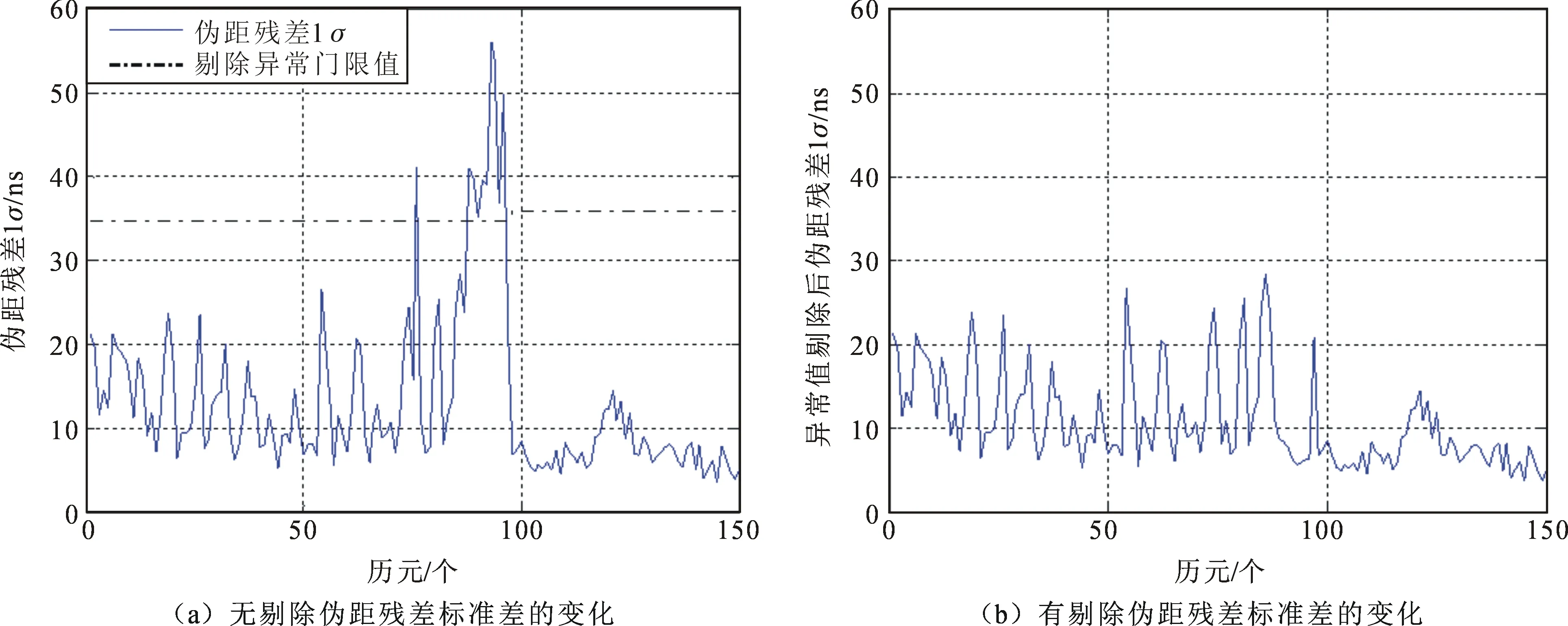
图4 多星随机故障检测和识别

④双星单故障

此场景为仿真数据,图5中可见星只有两颗时发生单星故障,在第300～400个历元间的单星伪距残差上叠加110 ns的粗差,此时由于冗余观测量少,传统方法检测此类故障存在瓶颈,而利用存储的历史伪距残差进行对比,可以鉴别出故障卫星,不过检测时间需要加长以减少误检概率。若时钟已完成驯服,可改用时钟模型预测钟差估计值作为参考进行鉴别,这样可以降低检测门限,提高检测灵敏度。

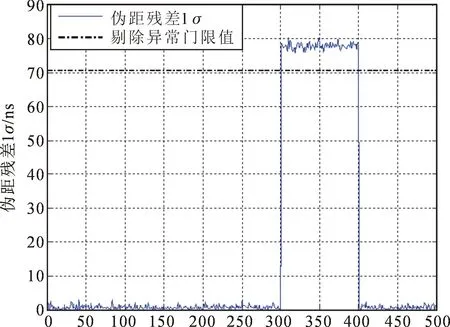
图5 双星单故障检测

3 结语

通过仿真和实测数据的验证表明改进后的T-RAIM算法可用性强在可见星少和多星故障时也具备检测能力,另外故障检测门限低,缩短微小缓变故障检测时间,提高了北斗定时服务的可用性和完好性。相信随着北斗全球系统的逐步建成,北斗授时服务将迎来更加广阔的市场。