结构动力有限元分析中材料阻尼模型的注记

宋雪飞

上海建工集团工程研究总院 上海 201114

有限元技术在土木工程振动计算中的广泛使用，使得结构动力建模越来越精细化，导致了自由度数目巨大的计算模型。对于大量自由度的结构动力模型，阻尼模型和参数的选取是关键问题之一。

基于对材料振动耗能的物理机制方面的一些试验现象的观察，先后提出了与速度呈线性关系的黏滞阻尼假定、与速度呈线性关系的频率相关的黏滞阻尼假定和复阻尼假定等，这些阻尼假定和相关分析方法在文献[1-2]中得到了比较系统的论述。但由于阻尼现象与机理的复杂性，目前尚没有建立一般的材料阻尼理论来用于土木工程结构的动力设计。

因此建立具有理论和试验数据基础、适用于大规模有限元结构动力计算的阻尼理论与模型仍是一个有待解决的重要问题。

本文基于工程材料存在振动耗能常数的假定和结构动力有限元分析理论，推导出了简单的结构材料阻尼矩阵，与构造质量矩阵和刚度矩阵的规则完全相同，便于动力有限元分析过程的实现。

同时，根据桥梁环境振动阻尼实测数据和模型桥梁阻尼的测试数据，验证了材料振动耗能常数的存在性。振动解答比较结果表明，基于材料振动耗能常数存在假定得到的振动反应的结果与复阻尼假定下振动反应的结果在数学表达形式上相同，数值差别可以忽略不计。

1 基于有限元理论的材料阻尼模型

1.1 材料的振动衰减常数与单元阻尼矩阵

考虑惯性效应和阻尼效应的弹性介质动力平衡方程如式（1）所示[3]：

式中：A——微分算子矩阵；

σ——应力向量；

p——体力向量；

ρ——质量密度；

ü——加速度向量；

η——振动耗能常数；

式（1）对于阻尼力的处理依赖于2个假定：

1）材料振动耗能常数η存在。

2）结构阻尼力假定等于材料的振动耗能常数η与材料振动速度的乘积。

根据有限元基本原理，基于式（1）可以得到结构的动力学有限元方程〔式（2）〕：

式中：M——结构质量矩阵；

C——结构阻尼矩阵；

K——结构刚度矩阵；

u——节点位移向量；

——节点加速度向量；

p(t) ——节点动力荷载向量。

基于式（1）得到的单元质量矩阵Me和单元阻尼矩阵Ce如式（3）所示：

式中：Ne——单元形函数。

由式（3）可得式（4）：

式中：αe——材料的振动衰减常数。

由式（4）可知，基于式（1）得到的单元阻尼矩阵Ce与单元质量矩阵Me成比例，比例系数为αe。当在单元层面上采用Rayleigh阻尼假定，并且只考虑质量相关项时，可以得到与式（4）相同的结果。

αe并不取决于单元材料的振动耗能常数ηe和质量密度ρe的值，而是取决于它们的比值。确切地讲，αe并不是逐个单元变化的，而是因材料不同而变化的。对于单一材料构成的结构，αe对全结构取常数α，此时C=2αM，结构动力学方程（2）可以写为：

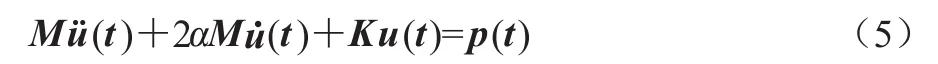
当结构不同区域由不同材料构成时，应根据不同区域确定不同的α值。此时用式（4）计算单元阻尼矩阵Ce，并根据与单元质量矩阵Me集成结构质量矩阵M相同的集成规则集成单元阻尼矩阵C。本文的讨论从式（5）开始。

1.2 振型阻尼比与振型频率之间的理论关系

记由质量矩阵M和刚度矩阵K构成的数学特征值问题所对应的特征值为ω21、ω22、…，特征向量为φ=[φ1,φ2,…]。作变换u=φx，利用φ与质量矩阵M和刚度矩阵K的加权正交关系（且φ关于质量矩阵M归一化）可以得到：

根据黏滞阻尼假定中振型阻尼比定义，式（6）可以写为：

比较式（6）和式（7）可知：

由于材料的振动衰减常数α仅依赖于材料特性，根据式（8），必然得到振型阻尼比ζj与振型频率ωj的乘积为常数的结论。

1.3 阻尼比和自由振动频率关系的试验结果

图1～图3是3座大桥的振型阻尼比和振型频率的实测结果，以及得到ζjω j的结果。由图可见，振型阻尼比随振型频率的增大呈衰减趋势，而ζ jω j则基本可以假定为一个常数。图4是猎德大桥（主跨167 m＋219 m，自锚式悬索桥）几何相似比1/50的模型在振动台进行白噪声激励所识别得到的自由振动频率和阻尼比的结果。其与前3座大桥的实测结果所反映的规律相同。

图1 苏通长江公路大桥振型阻尼比和自由振动频率的实测结果

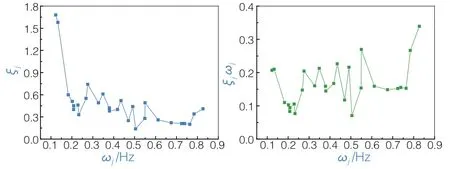
图2 西堠门大桥振型阻尼比和自由振动频率的实测结果

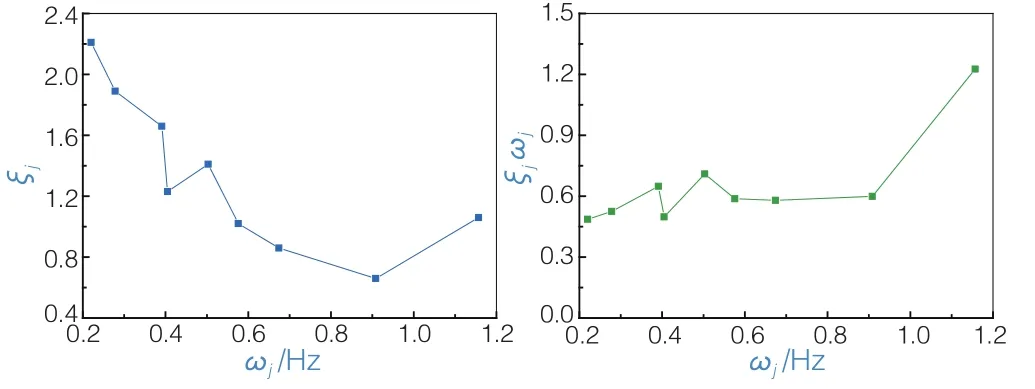
图3 红光大桥振型阻尼比和自由振动频率的实测结果

图4 猎德大桥模型（几何相似比：1/50）阻尼比与自由振动频率的实测结果

可见，振型阻尼比ζj与振型频率ωj之积为常数这一理论结果得到了桥梁原型和模型实测数据的有力支持，验证了前述材料振动耗能常数η的存在性，表明这是材料耗能机理的一个更符合实际的描述。同时也间接支持了与速度成线性关系的黏滞阻尼假定的合理性。

上述试验测试结果表明，通常采用的常振型阻尼比假定缺少试验测试数据的支持，不是一个合理的假定，特别是对具有大量动力自由度的结构进行有限元计算时。试验结果也辅证了前面数字解答的结论。

2 复杂结构情况

多数土木工程结构是一个复杂体系，耗能机制十分复杂，可分为材料阻尼、节点阻尼和界面阻尼。仅就材料阻尼而言，由于结构的不同部分由不同材料制作，因此材料耗能常数η和振动衰减常数α对于结构不同部分一般不同，也就是说不能针对全结构取相同的α。在这种情况下，结构的振动方程不能写为式（5），而只能写为式（2）。

在结构动力有限元建模中，如果不考虑非线性问题，结构的节点阻尼、界面阻尼以及人工阻尼一般可以描述为集中参数的黏滞阻尼。这样在形成结构体系的材料阻尼矩阵后，可以将其他阻尼作为集中阻尼，按照动力有限元总体阻尼矩阵与单元阻尼矩阵的关系，计入这些阻尼效应。

在上述复杂阻尼情况下，结构的阻尼矩阵不能通过无阻尼实振型解耦。如果仍要坚持采用向量叠加法计算结构的振动反应，则必须解算实对称矩阵（也可以是实非对称矩阵）的复特征值问题。关于这一问题的讨论可参见文献[4-7]。

3 结语

通过本文的研究工作，得到了以下结果和结论：

1）提出了工程材料存在振动耗能常数假定。基于此假定，在理论上证明了结构振型阻尼比和振型频率的乘积为常数的结论，3座原型桥梁和1座模型桥梁振型阻尼比和振型频率的实测数据验证了上述理论结论和材料存在振动耗能常数假定的合理性。

2）基于材料存在振动耗能常数的假定，给出了面向大量自由度土木工程结构动力有限元分析的阻尼矩阵构造方法，其规则与构造质量矩阵和刚度矩阵的方法相同，便于动力有限元方法的软件实现。

3）本文阻尼假定下，结构动力学方程和解答以实数表达，避免了复阻尼假定下繁琐的复数运算。