考虑多输入影响的高层建筑结构模型模糊控制

张微敬， 刘晓飞

(北京工业大学 建筑工程学院, 北京 100124)

主动控制技术是结构减振的有效手段,是动力学、控制、计算机、测试技术与材料科学等诸多学科的综合[1，2]。土木工程中,结构往往存在不确定的因素以及复杂的动力学特性,基于经典控制理论和现代控制理论的控制方法不能适应这一复杂系统的控制问题。近年来模糊控制由于其不依赖精确的数学模型、易于结合专家知识、鲁棒性好的特点，在结构控制领域受到广泛关注[3～9]。

在模糊控制算法中,模糊规则是实现其控制效果的关键。许多学者对如何获取模糊规则进行了研究，提出了多种有效的方法[10～13]。另一方面，对于设置主动质量阻尼器(Active Mass Demper,AMD)系统的模糊控制，已有研究多采用顶层位移和速度作为输入的两输入单输出模糊控制；对于地震作用下的高层建筑结构减振控制，如果仅利用顶层位移和速度信息，往往造成控制效果的降低。文献[14]进行了两输入单输出、三输入单输出和四输入单输出的模糊仿真分析，表明多输入模糊控制效果更好。但多输入模糊控制提取的模糊规则数目较多，会导致时滞现象，不利于实际应用。此外，主动控制研究主要以算法研究为主[15～19]，试验研究相对较少[20～24]，尤其对于大比例的高层建筑结构模糊控制的试验研究还不多见。

本文首先通过聚类算法进行模糊规则提取，并设计两输入单输出模糊控制器和考虑多输入影响的修正两输入单输出模糊控制器，通过对12层钢框架模型结构的模糊控制仿真分析和振动台试验研究，验证考虑多输入影响的模糊控制算法的有效性，为高层建筑结构的主动模糊控制应用提供参考。

1 基于FCM聚类算法的模糊控制规则提取

自Ruspini提出了模糊划分的概念以后，模糊聚类理论和方法迅速蓬勃发展起来，相继提出了多种聚类方法。实际中应用最为广泛的是基于目标函数的模糊聚类算法，模糊C均值聚类(Fuzzy C-Means，FCM)算法即是这种算法[25]。FCM算法把聚类归结成一个带有约束的非线性规划问题，通过优化求解获得数据集的模糊划分和分类。这种算法设计简单、解决问题的范围广，并且易于在计算机上实现[26]。针对建筑结构振动控制数据量大的特点，本文采用FCM聚类算法进行模糊规则的生成与提取。

1.1 数据预处理

以12层钢框架结构模型为控制对象，地震波采用的是EL Centro波(NS，1940)，加速度峰值为110 gal，采用线性二次型(LQR)经典最优控制算法产生的顶层位移、顶层速度以及控制力时程作为样本数据提取模糊规则。该12层模型参数中质量和刚度参数与下文仿真分析和试验研究的模型参数有一定差异，以便验证模糊控制算法的鲁棒性。

样本数据格式为两输入一输出，两输入分别为结构位移x和速度v，输出为作用在结构上的控制力u，采样周期0.01 s。形式如下：

(x1,v1,u1)，(x2,v2,u2)，…，(xn,vn,un)

(1)

所有数据样本组合在一起，构成样本矩阵(n×3)，预处理操作针对该矩阵进行，本文中采样数据个数为n=2689。数据预处理步骤不再赘述。

为更好的观察聚类中心在数据中的分布，作以下处理：首先将每一组数据按一定比例放大或缩小，然后把每一组大于零或小于零的数据与采样时间分别组合为二维数据。图1给出数据u>0的聚类结果，通过聚类产生了正大(PB)、正中(PM)及正小(PS)三个聚类的中心点。

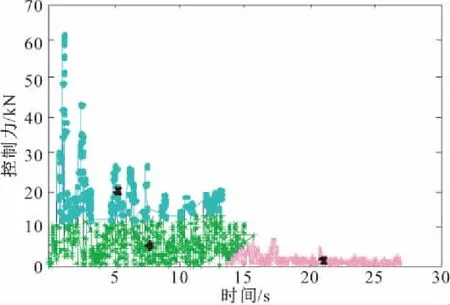
图1 控制力u>0聚类图

1.2 模糊输入输出隶属函数及规则生成

输入输出空间的模糊划分包括各变量论域的确定、隶属函数的选取、隶属函数的分布等。假设位移、速度、控制力3个变量的取值范围分别为[x-,x+]，[v-,v+]，[u-,u+]，取值范围指涵盖该变量所有取值点的范围，各隶属函数中心点的坐标也包括在该范围内。隶属函数采用三角形隶属函数。对输入输出模糊空间进行划分，将已知数据分别定位于最大隶属度对应的区间上。两个输入数据分别在各自区间上对应到其模糊变量，取数据对中的输出作为模糊规则的输出，从而形成一条if——then规则；两个输入变量的模糊划分按照全排列的方式组合，只要样本有足够的代表性，经过聚类处理的模糊空间划分所产生的控制规则能够满足完备性的要求[27]。

提取规则的过程类似于模糊神经网络，限于篇幅，这里不再赘述。

经以上步骤，得到输入输出隶属函数和模糊控制规则表。图2给出了输入变量位移、速度和输出变量控制力的模糊隶属函数。参考该模型的无控工况及LQR有控仿真分析结果，将位移论域取[-10 10] mm，速度论域取[-150 150] mm/s，控制力取[-3 3] kN。表1给出了经过FCM聚类算法得到的模糊控制规则表。其中，NB，NM，NS，ZO，PS，PM，PB分别表示负大、负中、负小、零、正小、正中、正大。

图2 输入输出变量隶属函数

2 模糊控制仿真分析

对顶层设置AMD装置的1∶8十二层钢框架模型结构进行模糊控制仿真分析，模型结构参数如表2所示，框架模型基本周期为0.26 s，自振频率为3.9 Hz。仿真时采用的地震波分别为Taft波(NW，1952)、EL Centro波(NS，1940)，加速度峰值调至110 gal，根据模型设计的相似关系，将时间近似压缩为原来的0.4倍。

表1 模糊控制规则

表2 模型结构参数

为研究地震作用下高层建筑结构考虑多输入影响的模糊控制，首先需要确定多输入变量的选择。以减小顶层位移为目标，通过多个工况的仿真分析对比，得出除考虑顶层位移和速度外，选择中间层的位移和速度，控制控制效果好于选择其他层的位移和速度或者选择其他两层的位移或速度。因此，本文仿真计算包含以下3种工况：

(1) 无控；

(2) 工况1：由第12层位移和速度构成的两输入模糊控制；

(3) 工况2：由第6层位移和速度、第12层位移和速度构成的考虑多输入影响的修正两输入模糊控制；

图3为MATLAB/Simulink中Fuzzy模块里设计的模糊控制器，图中给出了考虑多输入影响的部分框图。由图3可知，在模糊输入量进入控制器之前，分别提取模型结构第6层及第12层位移和速度，然后将其整合为1组位移向量和1组速度向量，进入到模糊控制器两个输入端，以此实现考虑多输入影响。

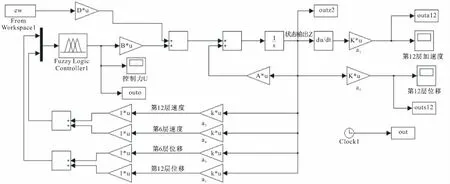
图3 Simulink仿真结构

利用Simulink对上述工况进行仿真分析。表3，4分别给出了Taft波、EL Centro波输入下，模型结构各工况下相对位移反应峰值，图4，5分别给出了Taft波、EL Centro波输入下，各工况模型结构第6层和第12层相对位移时程曲线及控制力时程曲线。

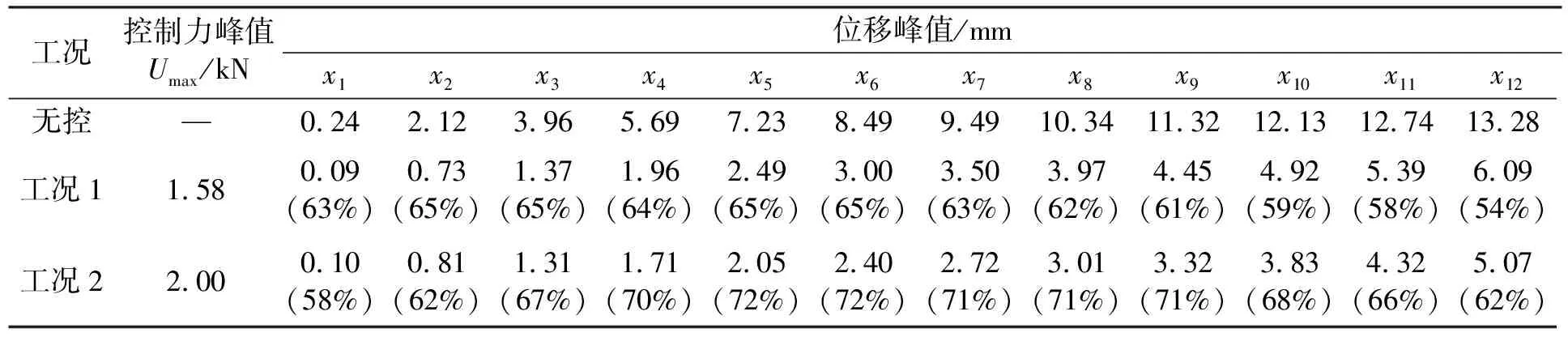
表3 Taft地震波输入下各层相对位移峰值比较

注：括号内的百分数表示各工况下每层位移相对于无控的减振效果；表中x1,x2,…,x12分别表示模型结构第1层，第2层，…，第12层相对位移

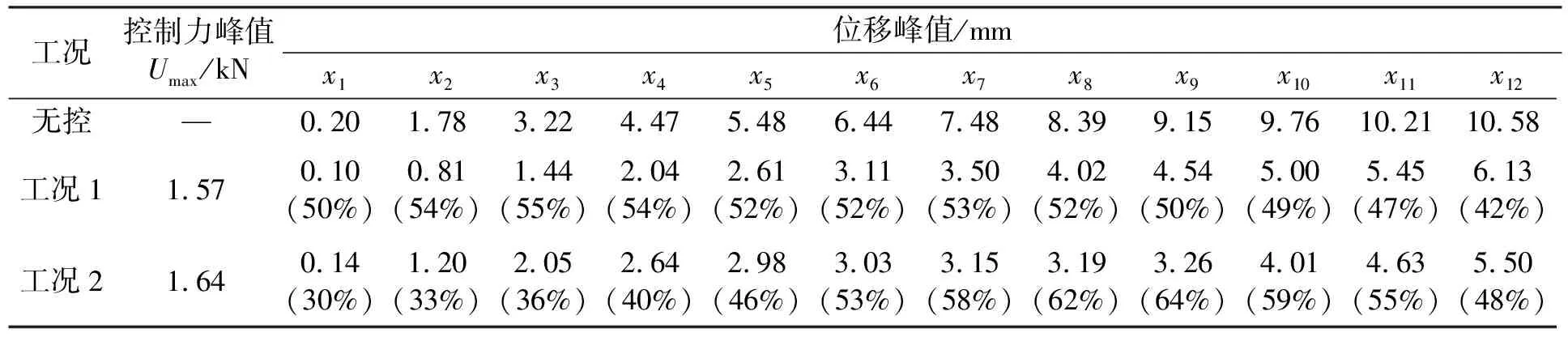
表4 EL Centro地震波输入下各层相对位移峰值比较

注：括号内的百分数表示各工况下每层位移相对于无控的减振效果；表中x1,x2,…,x12分别表示模型结构第1层，第2层，…，第12层相对位移

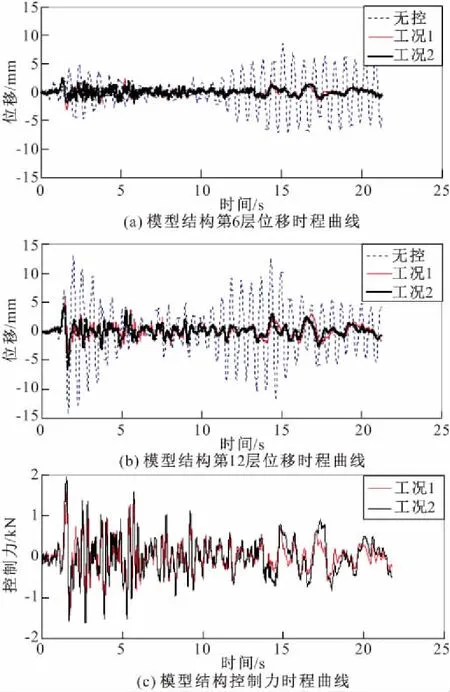
图4 Taft地震波输入下模型结构相对位移及控制力时程曲线

图5 EL Centro地震波输入下模型结构相对位移及控制力时程曲线

由表3和图4可以看出，在峰值为110 gal的Taft波作用下，工况1，2均有效减小了模型结构的地震反应，各层相对位移反应峰值的控制效果均在50%以上。除底部2层外，工况2的控制效果均好于工况1，第6层和第12层位移反应峰值比无控分别减小72%和62%，比两输入普通模糊控制分别减小20%和17%。由表4和图5可以看出，在峰值为110 gal的EL Centro波作用下,工况1，2同样有效减小了模型结构的地震反应。其中，底部5层以下工况1的控制效果略好，第6层位移反应峰值2个工况相差不大，均比无控减小52%，模型结构第12层位移反应峰值工况2比无控和两输入普通模糊控制分别减小48%、10%。相比普通两输入模糊控制，Taft地震波作用下工况2控制力峰值略大，但仍在控制器作用力±3 kN范围内；EL Centro波作用下，工况1和工况2的控制力峰值接近。显然，考虑多输入影响的修正模糊控制在所需传感器和控制力峰值均增加不多的情况下，控制效果比普通两输入模糊控制效果更好。

3 模型结构振动台试验

3.1 试验平台与采集系统

模型结构AMD模糊控制振动台试验是在哈尔滨工业大学力学与结构实验室完成的。地震模拟振动台台面尺寸为3 m×4 m，振动台作动器最大出力为250 kN，最大行程为±250 mm，频率范围为0～25 Hz，振动台最大承重为15 t。AMD系统作动器行程150 mm，最大出力为20 kN，作动器配有位移传感器和荷载传感器。

试验主要测量结构的状态向量(位移、速度)。位移测量采用FT71型位移传感器，根据仿真分析结果，位移传感器行程分别选取±100，±150 mm；速度测量采用B&K加速度计，通过多功能电荷电压滤波积分放大器将加速度转换为速度；其余加速度测量采用国产加速度计。

基于MATLAB/Simulink设计控制系统，将连续的控制系统离散化。进入dSPACE中定义输入输出，自动生成模型实时代码。利用ControlDesk采集数据，数据实时进入预先编写的算法内，通过一系列运算得出控制力，ControlDesk将该控制力作为输出量，输出到MTS中。MTS接收到控制力后向AMD作动器发出指令，从而推动AMD运动，达到减小结构地震反应的目的。

3.2 试验结果

图6给出了顶层设置AMD的12层模型结构。框架结构总质量为9290 kg(包括混凝土配重块和AMD质量)，其中AMD质量为170 kg，接近结构总质量的2%。本试验只在近台面层、4层、6层、8层、11层和12层布置了位移和加速度传感器。其中，底层、6层及12层采集的数据作为控制器输入信号，其余数据用于减振分析。

试验中首先对顶层作用有AMD装置的模型结构进行了时间压缩为0.4倍、峰值为110 gal 的Taft波地震激励下无控时结构反应的研究，以进行参数识别。为验证模型修正的效果，采用试验中台面输入的Taft地震记录进行了无控仿真计算，按修正后的模型结构参数(表2)得到的结构顶层相对位移反应与试验所得顶层位移反应对比见图7。可见，无控仿真与试验得到的结构反应形状、大小十分接近，表明修正后的结构模型参数是准确的。

图6 顶层设置AMD的12层模型结构

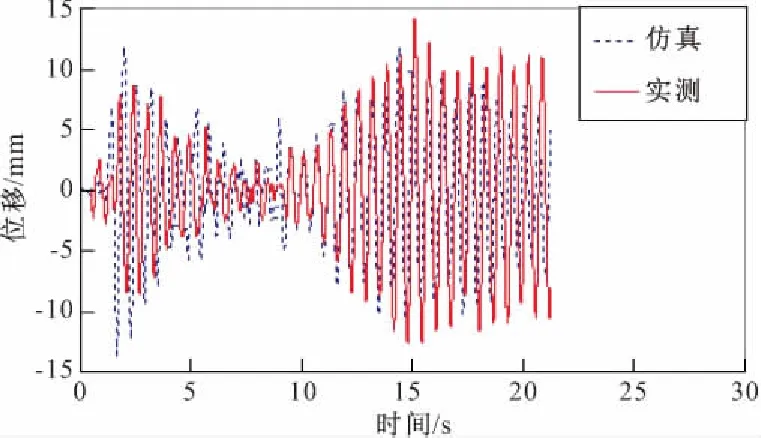
图7 无控工况下结构顶层位移反应对比

表5和图8为Taft波输入下实测的模型结构相对位移峰值和位移及控制力时程曲线。由表5和图8可知，在峰值为110 gal的Taft波输入下，相比无控，工况1、2均能有效减小模型结构地震反应，各监测层相对位移反应峰值的控制效果达到50%以上。其中，考虑多输入影响的工况2的控制效果更好，模型结构顶层相对位移反应峰值比无控减小70%，比两输入普通模糊控制效果提高12%；但相比普通两输入模糊控制，控制力峰值有所增大。数值仿真与试验结果相吻合，验证了修正的两输入模糊控制算法的有效性。

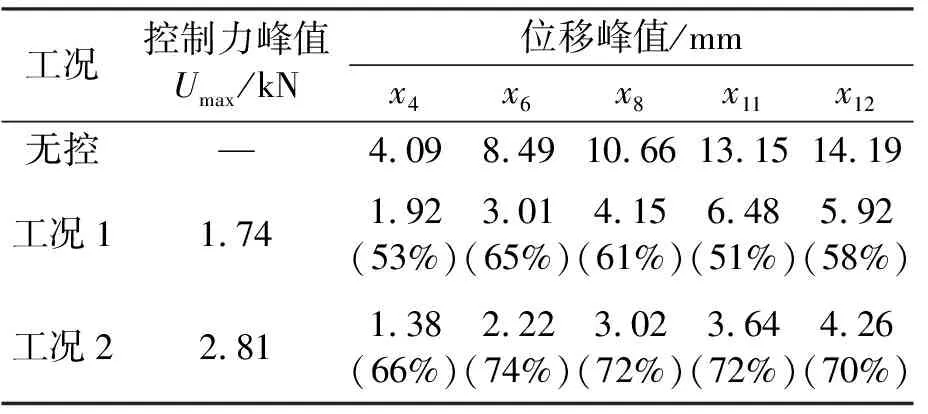
表5 Taft地震波输入下实测模型结构相对位移值

注：括号内的百分数表示各工况下每层位移相对于无控各层位移的减振效果；表中xi表示钢框架模型结构第i层相对位移

图8 Taft地震波输入下实测相对位移及控制力反应时程曲线

4 结 论

本文对顶层设置AMD控制装置的12层钢框架模型结构进行了模糊控制仿真分析和试验研究，得到以下结论：

(1) 采用FCM聚类算法，从初步模型得到的受控结构反应数据中，可方便提取到所需模糊控制规则；

(2) 针对高层建筑结构振动模糊控制，提出了考虑多输入影响的修正两输入模糊控制策略。仿真分析表明该算法减振效果优于普通两输入模糊控制；

(3) 成功完成了大比例高层建筑结构AMD主动模糊控制振动台试验研究。试验结果进一步验证了考虑多输入影响的模糊控制算法的有效性，该算法对顶层相对位移反应峰值的控制效果达到70%，为高层建筑结构模糊控制工程应用提供一定的参考。