沌口长江公路大桥弹性—阻尼复合式减震装置的应用

陈毅明， 付 坤， 杨 健， 任 蒙， 孙 远

(1. 中交城市轨道交通设计研究院有限公司， 湖北 武汉 430056； 2. 中交第二公路勘察设计研究院有限公司， 湖北 武汉 430056；3. 华中科技大学 土木工程与力学学院， 湖北 武汉 430074)

国内部分已建缆索承重大跨度桥梁，运营几年后，梁端伸缩缝损坏的现象较普遍[1]，有的甚至出现墩顶支座损坏的情况。分析其原因，这些桥梁均为采用传统液体黏滞阻尼器的半漂浮结构体系。采用阻尼器的目的是为了减小桥梁结构的地震作用效应[2]，而对车辆、温度等常遇荷载产生的梁端纵向位移和索塔及钢主梁、斜拉索等构件应力状态等问题不够重视。特别是传统阻尼器不能使主梁复位，一段运营期后，梁端累积位移往往超出伸缩缝的允许值，导致相应支座出现大偏位及磨损[3]。

本文结合沌口长江大桥，在塔梁之间设置新型弹性—阻尼复合式减震装置，分析其对大桥静力、动力性能以及稳定性的影响[4]。

1 工程概况

沌口长江公路大桥是首座跨越长江的双向八车道高速公路特大型桥梁，设计速度为100 km/h。跨江主桥采用主跨760 m双塔双索面PK钢箱梁，PK钢箱梁全宽46.0 m(含风嘴及布索区)，综合抗风稳定性要求、建筑景观等因素，主桥采用钻石型索塔，桥型布置及索塔结构如图1，2所示[5]。

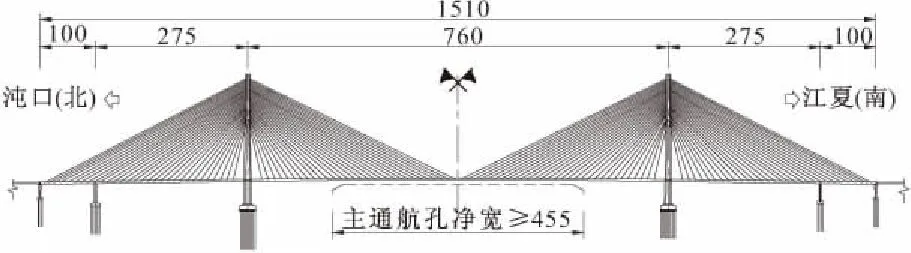
图1 桥型立面布置/m

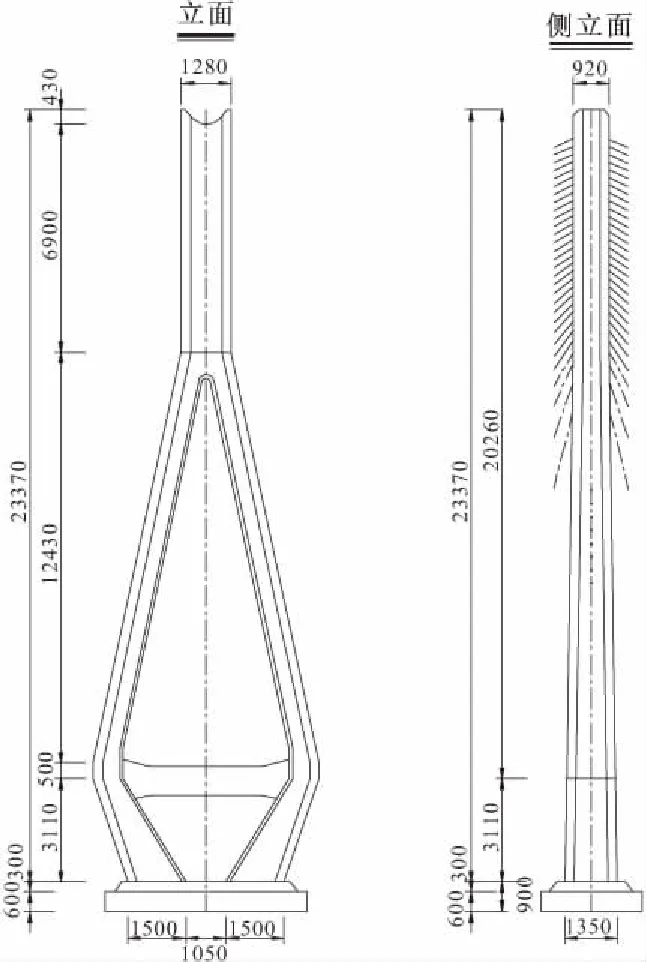
图2 索塔立面、侧面/cm

跨江主桥主体结构采用半漂浮体系，索塔位置设置竖向支座、横向抗风支座、纵向弹性—阻尼器连接；辅助墩位置设置竖向支座；过渡墩位置设置竖向支座(横向约束)。

2 弹性—阻尼复合式减震装置

装置构造图如图3所示。

图3 弹性—阻尼复合式减震装置

如图3所示，装置主要由阻尼腔体1和弹簧腔体2两部分组成。阻尼腔体1内有活塞杆3和阻尼介质，该活塞杆3为双出杆的形式，阻尼腔体1外壳一端接接长套9，接长套9与右球铰座5相连。弹簧腔体2内设有弹簧装置7，该弹簧装置7设置在阻尼腔体1径向外部或轴向，弹簧腔体2侧面两端设有阻力块8，弹簧腔体2外壳与左球铰座4相连，左球铰座4与活塞杆3连接，左球铰座4带动活塞杆3在阻尼腔体1内往复运动，并带动弹簧腔体2外壳一起运动，弹簧腔体2往复运动使弹簧装置7压缩，当弹簧行程较大时，弹簧腔体2内增设滑动块6随着弹簧装置变短、回复，在弹簧腔体2中往复运动。阻尼器工作时，左球铰座4带动活塞杆3相对右球铰座5运动，阻尼介质被迫通过活塞上的孔隙或间隙，产生摩擦、节流、阻尼效应，从而将阻尼器受到的外力所做的功转化为阻尼介质的内能，将外力所做的功消耗掉。同时，弹簧腔体2两端的阻力块8使弹簧装置7的弹簧被压缩，起静力弹簧作用。无论阻尼器被拉伸还是压缩，该弹簧装置7均被压缩。

这种阻尼器将弹簧装置7设置在阻尼腔体1外壳的径向外部或轴向，两端用圆螺母固定。阻力块8螺纹旋入弹簧腔体2外壳并焊接固定。弹簧腔体2与左球铰座4以螺纹和螺栓连接，并焊接固定。左球铰座4与活塞杆3螺纹连接，并用螺母固定。

3 结构抗震分析

进行抗震结构体系研究的目的，是寻求结构在强度、刚度、变形等指标上的最佳组合，使结构能经济地实现抗震设防目标[6]。本项目对结构体系的研究，着重研究塔、梁之间的连接方式。

大跨度斜拉桥采用飘浮体系来减小地震反应内力，实际上是通过延长周期来达到的。由于采用了飘浮体系的大跨度斜拉桥周期太长，而且自身的阻尼也比较低，会导致梁端产生过大的地震位移[7]。要减小梁端的位移反应，可以有两种途径：一是适当缩短结构的周期(增大结构的刚度)，找一个折中方案，兼顾力和位移；二是增大桥梁结构的阻尼。于是，为了控制大跨度斜拉桥的梁端地震位移，可以在塔、梁之间增设减震装置，主要有两类，第一类装置提供纵向刚度，第二类装置提供阻尼。而成功减小地震位移的关键，则在于选择合适的塔、梁连接装置，以及相应的合理参数。下面通过非线性时程分析，比较塔、梁间弹性刚度变化和阻尼参数变化，以及弹性—阻尼复合装置对结构地震反应的影响。

3.1 塔、梁间弹性刚度对地震反应的影响

为了分析塔、梁间弹性连接装置的弹性刚度K对斜拉桥结构地震反应的影响，抗震分析设定了一系列的K值进行了地震反应分析。包括：K=0，000，4000，6000，10000，20000，25000，30000，40000，50000，1.0×105，5.0×105，1.0×106，5.0×106，1.0×1010kN/m共15个值，其中，K=0相当于全飘浮体系，K=1.0×1010kN/m相当于塔、梁纵向固结体系。每个K值对应的地震反应结果都取3组地震动加速度时程所产生的地震反应的最大值，总共计算了45个工况。

三组地震动x方向(顺桥向)加速度时程图如图4所示，图中E2表示设防标准为50年超越概率2%，地震输入方式为：纵向+竖向，其中竖向地震动时程采用0.5倍纵向地震动时程[8]。

图4 地震动加速度时程

如图5～8所示(均指北侧桥塔、梁端，下同)，计算分析表明，随着弹性连接装置的弹性刚度的增大，梁端位移以及塔顶位移总体显著减小；而塔底剪力和弯矩并非完全单调增大，随着弹性连接的刚度增大，传递荷载增大，直至墩顶出现塑性变形，故塔底剪力和弯矩在K=10000 kN/m出现峰值后迅速减小，在K=40000 kN/m后单调缓慢增大。可见，通过综合考虑弹性连接装置的弹性刚度对塔顶、梁端位移与塔底剪力及弯矩的影响，选取合适的弹性刚度，可以有效地减小塔顶、梁端以及塔、梁间的相对位移，而塔底剪力和弯矩增加基本较少。

图5 弹性连接装置的弹性刚度对梁端位移的影响

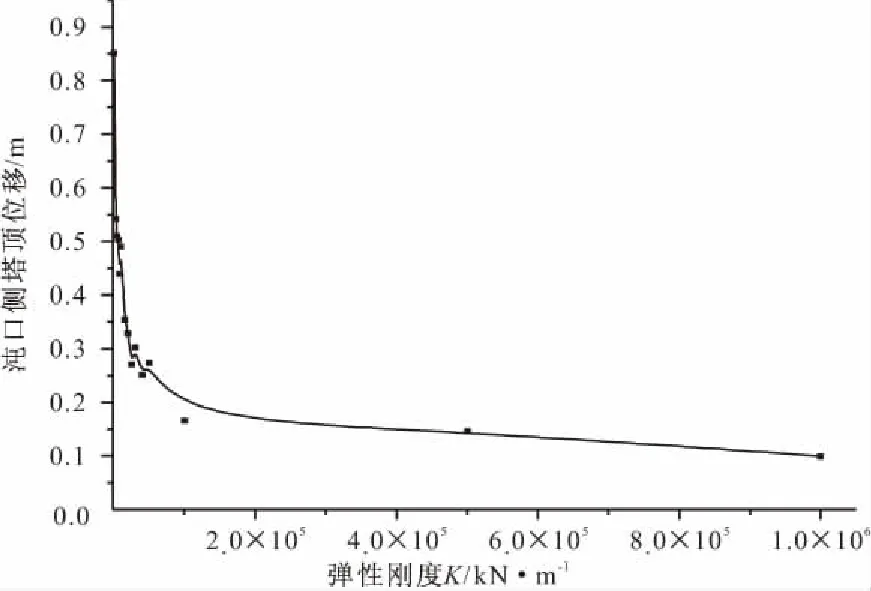
图6 弹性连接装置的弹性刚度对塔顶位移的影响

图7 弹性连接装置的弹性刚度对塔底剪力的影响

图8 弹性连接装置的弹性刚度对塔底弯矩的影响

限于篇幅，仅列出全飘浮(K=0)、弹性连接(K=6.0104kN/m)、固结(K=∞)体系的地震反应进行比较，如表1所示。

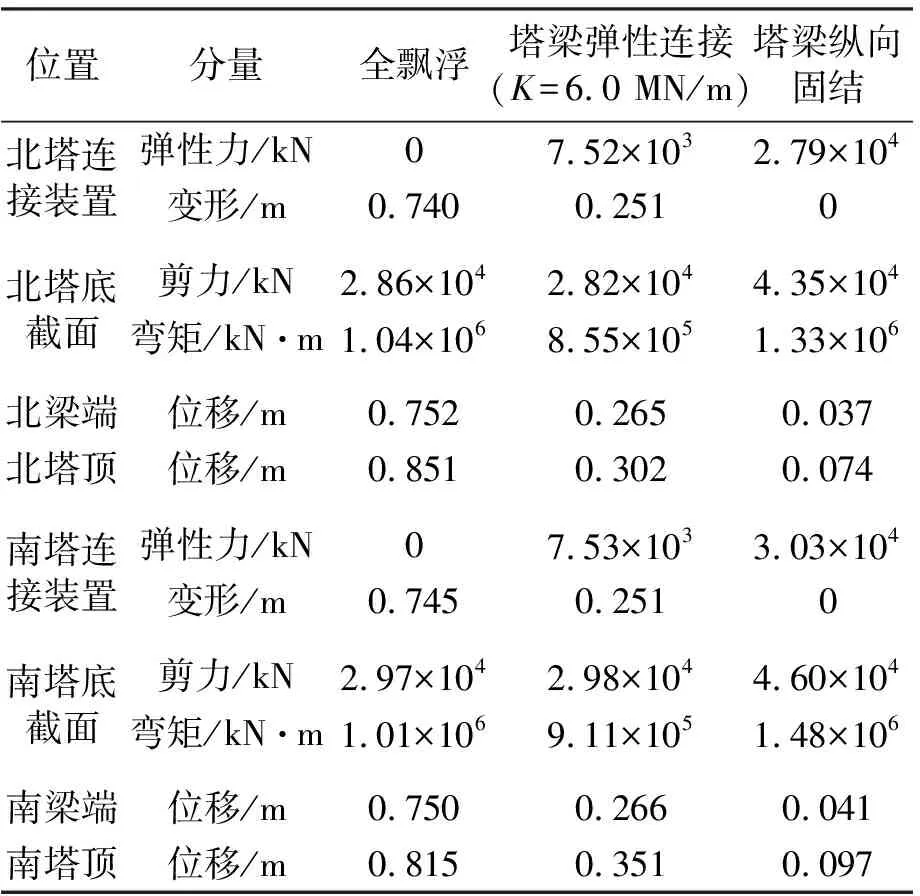
表1 三种结构体系的地震反应比较

注：塔梁弹性连接K=60 MN/m中，K=60 MN/m对应的是每塔处设置4弹性连接装置中4弹性连接装置的合计

表1中数据表明：弹性连接体系是全飘浮体系和塔梁固结体系之间的一个较好的折中方案，与飘浮体系相比，梁端位移减小了64%，而塔根的受力没有增加。

3.2 塔、梁间阻尼对地震反应的影响

阻尼器参数的选择，取决于设置阻尼器的目的：将主梁的纵向位移，索塔内力以及梁、塔的相对位移限制到设计要求的程度。

从抗震分析的角度出发，阻尼器的速度指数α的常用取值范围为0.3～1.0。设定α=0.3，0.4，0.5，0.7，1.0五个值，阻尼系数C设定为0，1000，2000，3000，4000，5000，6000，10000，15000，20000，30000共11个值，其中，C=0相当于全飘浮体系，总共55组参数。每组参数对应的地震反应结果都取3组地震动加速度时程所产生的地震反应的最大值，总共计算了165个工况。

图9～14分别为阻尼器的位移和阻尼力，梁端位移，塔底剪力、弯矩，以及塔顶位移随阻尼器参数的变化曲线。从这些图中可以看出，当阻尼器的速度指数α一定时，随着阻尼系数C的增加，阻尼器位移、梁端位移和塔顶位移单调减小(但位移减小速率变慢)，阻尼器的阻尼力单调增加，而塔底剪力和弯矩先减小后增加。在很大范围内，塔底剪力和弯矩都明显小于飘浮体系的反应，但如果阻尼系数过大，则会超过飘浮体系。虽然从理论上说，阻尼器的阻尼力只和速度(与位移反向)有关，不会直接叠加到结构的内力上，但实际上阻尼力和结构的弹性力是有一定程度的叠加的(尤其是阻尼器的指数较小时，如接近0.3)，而且阻尼越大，这种叠加越明显，所以当阻尼系数过大时，阻尼器会增加结构的受力。另一方面，当阻尼系数C一定时，阻尼器位移、梁端位移和塔顶位移随着阻尼器的速度指数α的增加而增加，阻尼器阻尼力则随着阻尼器的速度指数α的增加而减小。而塔底剪力和弯矩随速度指数α的变化趋势跟阻尼系数有关，当阻尼系数较小时，塔底剪力和弯矩随速度指数α的增大而增大，而当阻尼系数较大时，则相反。显而易见，设置阻尼器可以显著地减小塔顶位移、梁端位移、塔梁相对位移，同时还可以减小塔底剪力和弯矩。

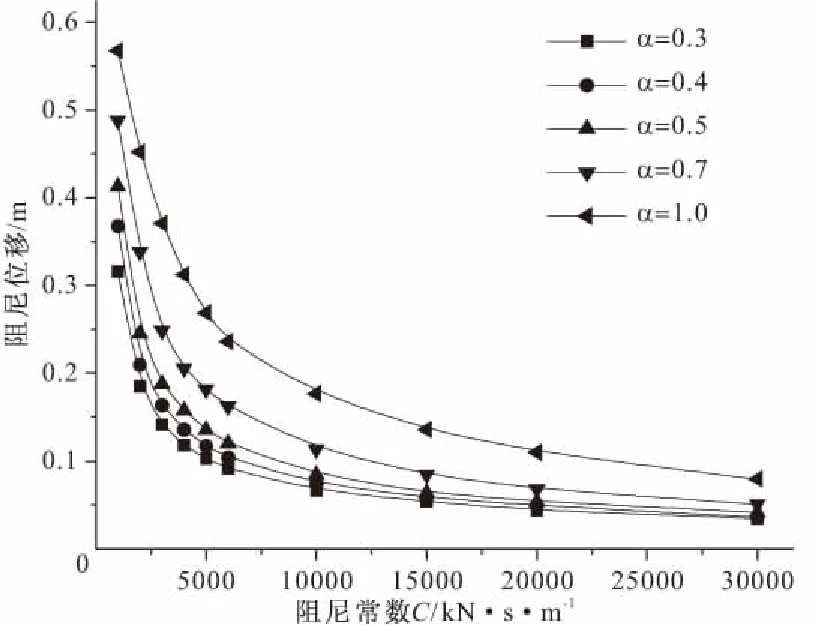
图9 阻尼器参数对桥塔处阻尼器位移的影响

图10 阻尼器参数对桥塔处阻尼力的影响

图11 阻尼器参数对梁端位移的影响

图12 阻尼器参数对桥塔塔底剪力的影响

图13 阻尼器参数对桥塔塔底弯矩的影响

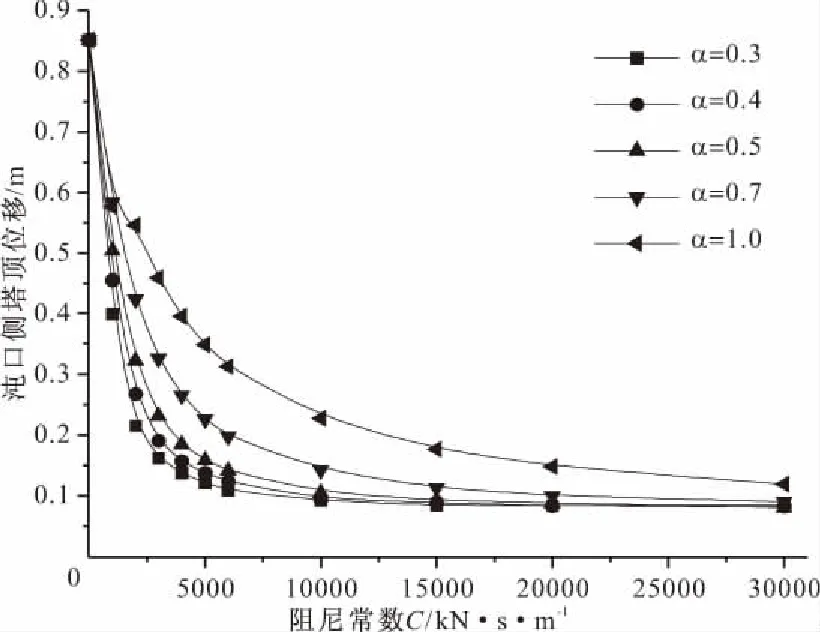
图14 阻尼器参数对桥塔塔顶位移的影响

综合考虑阻尼器位移及阻尼力、梁端位移、塔顶位移、主塔剪力和弯矩随阻尼器参数的变化情况，如果要求将主梁的纵向位移，梁、塔的相对位移控制在15 cm以内，建议选用阻尼系数C为10000，指数α为0.5(单塔处合计)的阻尼器，其最大变形速度为0.26 m/s；而如果要求位移控制在10 cm以内，建议选用阻尼系数C为20000，指数α为0.5(单塔处合计)的阻尼器，其最大变形速度为0.20 m/s，阻尼力和速度对应的单位分别为kN，m/s2。

表2对全飘浮体系，阻尼体系(C=20000，α=0.5)，以及塔、梁纵向固结体系的地震反应进行了比较，表中数据表明：设置阻尼器后，塔底剪力是飘浮体系的86%、纵向固结体系的56%；塔底弯矩是飘浮体系的68%、固结体系的49.8%(南北索塔的平均值)；而梁端位移是飘浮体系的11.6%、固结体系的2.2倍(南、北端平均值)。可见，设置阻尼器可以显著地改善整个斜拉桥的地震反应。

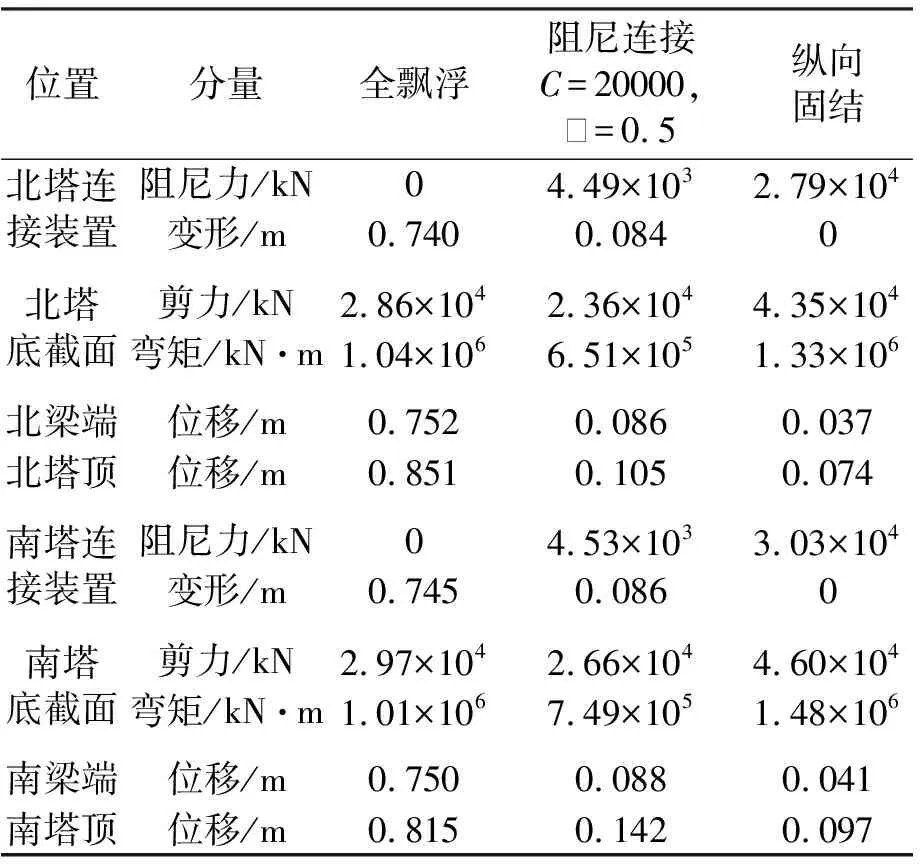
表2 三种结构体系的地震反应比较

注：塔梁阻尼连接中，C=20000为每塔处设置4弹性连接装置中4弹性连接装置的合计

3.3 塔、梁间弹性+阻尼对地震反应的影响

从上述分析可以看出，弹性连接装置和阻尼器均能有效地减小梁端的地震位移，但阻尼器的效果更为理想。

综合考虑静力和动力作用，塔梁连接装置采用“弹性+阻尼”复合减震装置，同时具备弹性连接装置和阻尼器的特点；该装置本构模型为：

F=KX+CVα

(1)

式中：F为阻尼力(kN)；V为阻尼器连接两端相对速度(m/s)；α为速度指数；X为阻尼器连接两端相对位移(m)。

表3，4对塔梁连接弹性刚K=1.2 MN/m(每塔)，阻尼参数分别取C=20000，α=0.5和取C=10000，α=0.5的地震反应进行比较。

表3 两类连接装置的减震效果比较

注：表中阻尼器及弹性参数均对应的为每桥塔处阻尼器总参数，下表同

表4 两类连接装置的减震效果比较

从表中可以看出：相对于传统阻尼器，弹簧阻尼器能减小塔顶、梁端位移，而对塔底剪力、弯矩影响较小。

4 结构静力分析

在塔梁之间增设适当刚度的弹性连接，不仅可以有效减小地震作用效应、控制梁端纵向位移，还能明显地改善其静力性能。此外，弹性连接还可以减小静力工况下主梁的位移，显著提高全桥二类稳定系数，从而增加全桥安全储备。

4.1 对桥塔、主梁及拉索受力的影响

静力受力时塔梁间弹性—阻尼复合连接器仅弹簧刚度发挥作用，静力分析采用MIDAS程序，在建立有限元模型时作了以下处理：

(1)主梁采用鱼骨梁的方式模拟，主塔采用梁单元模拟，斜拉索采用只受拉单元，在进行屈曲分析时，转换为桁架单元，辅助墩与过渡墩也采用梁单元模拟。

(2)桥塔处主梁通过弹性连接竖向支撑于桥塔下横梁上、横向支撑于塔柱上(横向支撑为单向受力)。

(3)斜拉索与主梁的连接采用弹性连接，塔梁连接处也采用弹性连接模拟。

(4)过渡墩、辅助墩、主塔及临时墩旁边的临时支架的支撑点以一般支撑模拟，采用与实际结构布置相同的支撑点数、相同的支撑位置、相同的支撑约束方向及约束。

(5)墩、塔及临时支架与地面的连接，采用节点弹性支撑。

表5～8给出不同弹簧刚度取值对桥梁结构受力的影响。

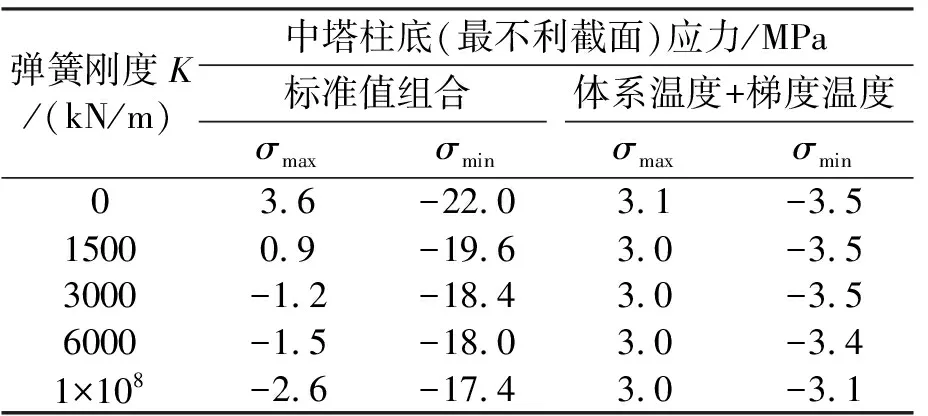
表5 弹簧刚度对桥塔受力的影响

当弹簧刚度超过一定值时，桥塔在标准值组合作用下以全压状态受力，有利于桥塔的耐久性。此外，对于大跨斜拉桥，塔梁间增设纵向弹性连接对于承受温度荷载总体是有利的。

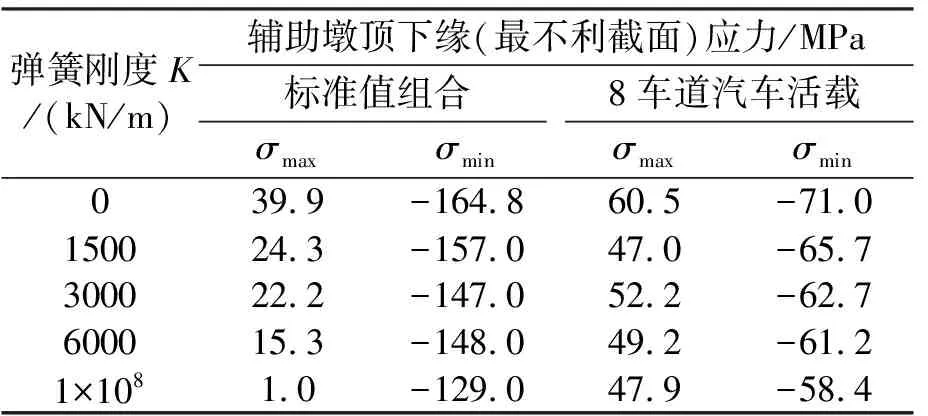
表6 弹簧刚度对主梁受力的影响

由表6可知，塔梁间纵向弹簧刚度的引入，改善了钢主梁的受力，降低了钢主梁疲劳应力幅。

表7 弹簧刚度对拉索受力的影响

注：S22号拉索位于辅助墩顶的梁段上。

分析结果表明，塔梁间设置纵向弹性连接，可减小斜拉索疲劳应力幅。但当弹簧刚度增加至相当于刚性连杆时，温度荷载导致拉索应力显著增加。

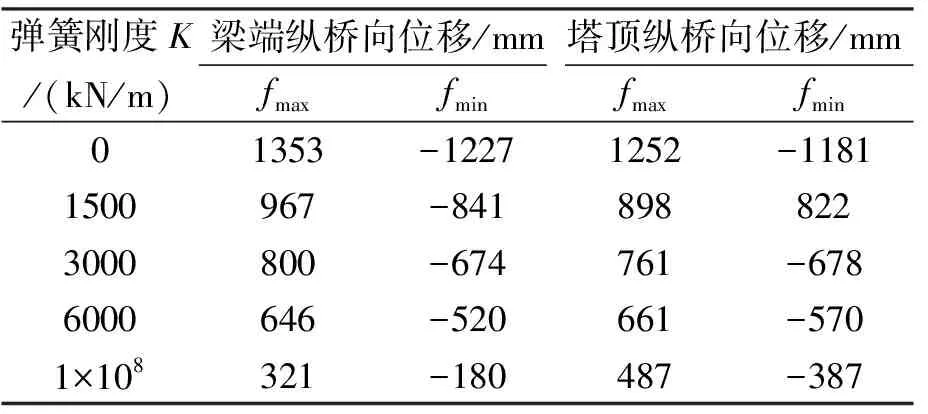
表8 弹簧刚度对位移的影响(标准值组合[9])

塔梁间设置纵向弹性连接，显著减小了全桥位移，减小了梁端伸缩缝的伸缩量、增加了其耐久性。

4.2 对全桥二类稳定的影响

稳定问题是以受压为主的桥梁在结构设计、施工中需要解决的关键问题之一。从斜拉桥的受力分析可知，主梁和索塔是以受压为主的压弯构件，其失稳情况应属于第二类稳定问题。二类稳定分析即考虑几何非线性及材料非线性的承载能力极限状态分析。本文采用ANSYS程序建立全桥模型(图15)。

图15 全桥二类稳定分析计算模型

主梁及桥塔采用beam188单元，拉索采用link180单元，钢材采用双折线理想弹塑性本构关系，混凝土采用GB 50010-2010《混凝土结构设计规范》[10]规定的本构曲线进行分析。分析结果表明，桥塔上塔柱底部截面最先达到承载能力极限的部位，破坏形态为压溃，从而控制全桥的二类稳定系数。表9给出不同弹簧刚度时相对于承载能力极限状态基本组合的二类稳定系数结果。

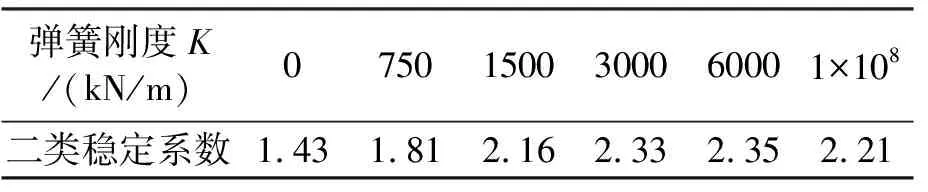
表9 弹簧刚度对全桥二类稳定的影响

由于在施加荷载时已考虑结构重要性系数、各项荷载分项系数及组合系数，故其二类稳定系数仅需大于混凝土材料的分项系数1.45即可保证全桥受力安全。由表9可知，塔梁间的纵向弹性约束可显著提高全桥二类稳定系数，但当弹簧刚度超过3000 kN/m后全桥二类稳定系数基本不再提高，当刚度相增加刚性连杆时二类稳定系数反而下降。

5 结 论

(1)本文提出的塔梁间弹性—阻尼复合连接器，其抗震性能与传统液体黏滞阻尼器相当，但其对大跨斜拉桥静力受力性能有明显提升，降低了索、梁、塔的内力及应力，改善了钢梁、拉索及伸缩缝等构件的耐疲劳性能，提高了桥塔的二类稳定系数，以较小的代价获得了大桥综合受力性能的显著提升。

(2)此外，该新型塔梁间弹性—阻尼复合连接器采用了创新的结构构造，将蝶形机械弹簧与液体黏滞阻尼器封装于一体(机械弹簧密封于防腐、润滑油中)，并设置了受力状态监控传感器，因此具有可靠耐久、维护方便、智能监控的特点。

(3)采用弹簧阻尼器装置后，静力工况得到改善，汽车荷载与温度荷载下斜拉索的疲劳应力，汽车荷载下大桥的纵向位移等都改善较多。综合考虑静力、地震等动力工况，推荐采用“弹簧阻尼器装置”。