基于遗传算法的摩擦摆TMD系统参数优化分析

吴玖荣， 李基敏， 孙连杨， 傅继阳， 段永定

(1. 广州大学 广州大学-淡江大学工程结构灾害与控制联合研究中心， 广东 广州 510006；2. 淡江大学 土木工程学系， 台湾 新北 25137)

随着我国经济的迅速发展和社会需要，近年来相继建造了大量高层和高耸结构。这类结构具有轻质高强、柔细化、低阻尼等特点，水平风荷载成为其结构设计的主要控制因素。当风致响应过大时，可以采用被动结构控制系统对高层和高耸结构进行风振控制。采用传统的调谐质量阻尼器Tuned Mass Damper (TMD)来进行结构风振控制的工程例子已经屡见不鲜，如台北101等的类似单摆TMD系统，但此类被动结构控制系统占据的结构空间比较大，且需要配置额外的阻尼系统。另一类摩擦摆系统FPS(Friction Pendulum System)自1985年由美国Zayas[1]提出， FPS系统依靠上部物体在基础底部隔震系统所设置的圆弧曲面滑道内的摩擦滑动来耗能，以达到消能减振的目的。FPS系统由于其造价低、易于维护且具有良好的自限、复位、摩擦耗能等性质[2，3]广泛应用于桥梁工程和建筑物的基底隔震设计中。为此，部分学者已研究把地震工程中常用的摩擦摆(FPS)隔震系统和常用的调频质量阻尼器(TMD)被动控制系统有机结合，形成一种新型的摩擦摆调谐质量阻尼器(FPS-TMD)被动控制系统，放置在高层建筑与高耸结构顶部，来达到对主体结构进行风振控制的目的[4]。FPS-TMD系统可以根据被控主体结构的双向不同频率设计出不同曲率半径进行双向风振控制，为使此类被动控制系统的风振控制性能达到最优，可以采用一定的优化算法来加以实现。一般来说虽然随着FPS-TMD质量的增加，主结构动力响应会降低，但基于经济性考虑，且TMD质量增加会增加结构额外的负担，故FPS-TMD系统的最佳设计参数中，质量比一般不作为控制系统优化设计参数。而两个方向的滑道半径、滑道与TMD质量块之间的摩擦系数，则一般可以作为此类被动控制系统的优化设计参数。

在现有优化算法中，基因遗传算法作为模拟自然界生物进化过程来搜索最优解的一种优化方法。其拥有生物学独特的高效、并行、全局搜索的特点。它不同于许多传统算法单点搜索的搜索方式，而是采用同时处理种群中多个个体的方法，同时对搜索空间中的多个解进行评估，因此其具有较好的全局搜索性。且由于基因遗传算法是采用适应度函数值来评估基因个体，不受连续可微的约束，因此限制条件大大缩小，使得其应用范围大大扩展。但考虑到基本基因遗传算法往往由于需要预先指定交叉、变异概率和惩罚系数的值，且其值在迭代过程中为定值不变，算法的寻优效果对该值的敏感性较大，易陷入局部收敛等不足之处，本文采用了自适应基因遗传算法，对其优化过程中所采用的交叉、变异概率和惩罚系数值可以在迭代过程中不断改变，克服了基本基因遗传算法的缺点，从而更加快速地获得全局最优值。

本文以广州新电视塔为实例，以其顶部有无设置FPS-TMD系统的主体结构顶部风致位移或风致加速度均方根之比最小作为风振控制优化设计目标，采用自适应基因遗传算法，对其顶部设置带双向摩擦摆TMD系统的相关参数高层建筑，进行风振控制条件下的系统参数(包括两个方向的滑道半径，滑道与TMD质量块之间的摩擦系数)最优化设计相关研究。

1 双向摩擦摆型TMD的动力行为

1.1 曲面的斜率最大方向和曲面方程

因为双向摩擦摆型TMD的质量块运动方向不一定在最大斜率方向上，而其恢复力却始终在最大斜率的方向上，因此在进行风振性能分析时，需先求出最大斜率的方向,并在此方向上进行动力分析[4]。对于任意曲面方程式(1)，其示意图如图1所示，xd、yd分别代表卡氏座标两方向的位移量：

图1 双向FPS型TMD滑动曲面

zd=f(xd,yd)

(1)

假定此曲面上任意一点的位移坐标为(xd，yd)，通过此点且平行于xd-zd平面及yd-zd平面的斜率分别为：

(2)

(3)

式中：sx为此点斜率在x方向分量，sy为此点斜率在y方向分量。可推得最大斜率的向量如图2所示，其最大斜率Smax和向量表示形式v分别为：

图2 双向FPS型TMD滑动曲面最大斜率向量示意

(4)

(5)

(6)

式中：α为通过点(xd,yd)且平行于yd-zd平面及xd-zd平面的斜率之比；i,j,k分别为三个平行于坐标系主轴的单位向量。

xd，yd分别为双向FPS型TMD两方向之位移量，任意一个如碗状的曲面,其示意图如图3所示, 其方程式可表示为公式(7)～(9)：

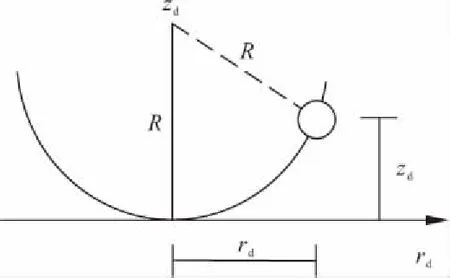
图3 双向FPS型TMD滑动曲面方程示意

(7)

(8)

(9)

式中：zd为滑动曲面上任意一点的高程；R为曲率半径；rd为滑动曲面上任意一点(xd，yd)投影到xd-zd平面后，与坐标原点的距离；Rx，Ry分别为FPS型TMD两方向的曲率半径。

1.2 双向FPS型TMD恢复力与最大摩擦力计算

在计算TMD恢复力时，其方向与最大斜率的方向相同，而最大斜率的大小恰好等于tanθ，其与xd-yd平面的夹角为θ，参考最大斜率向量示意图2，可以推得式(10)～(12)：

(10)

(11)

(12)

TMD质量块在滑道上滑动时的示意图如图4所示，由于TMD质量块滑动时摆动的角度θ很小，故向心加速度很小，予以忽略。由向心方向和切线方向的动力平衡方程，可得滑动曲面上任意一点的恢复力Frθ(t)和正压力N为：

图4 TMD质量块滑动示意

(13)

(14)

式中：Md为摩擦摆的质量。

由上述正压力N也可求得最大摩擦力Ffθ,max(t)：

(15)

式中：μk为FPS-TMD系统的滑道摩擦系数。

1.3 双向FPS型TMD的动力方程

由式(13)，(5)可知，当TMD质量块滑动时，其正压力会随着其在曲面上的位移坐标不同而改变，最大摩擦力以及恢复力均为非线性，都随着θ的改变而改变，双向FPS型TMD受风荷载w(t)作用时，忽略风荷载对质量块的作用，其运动方程可表示为：

(16)

将最大斜率的向量表达式(6)，投影至xd-yd平面后，与xd轴的夹角为φ，最大斜率向量示意图，可以推得下面两式：

(17)

(18)

根据式(17)，(18)，即可求得双向FPS型TMD在两方向的恢复力，先投影至xd-yd平面后，再分解至xd，yd两坐标方向，如式(19)，(20)所示：

(19)

(20)

式(16)为一组左边无刚度的运动方程，由于动力分析的需要，将恢复力分成两部分，一部分由TMD线性刚度所提供的线性恢复力，置于等号左边，另一部分则以式(19)，(20)所表示的总非线性恢复力扣除线性恢复力部分，置于等号右边从而可得运动方程：

(21)

2 顶部加装双向FPS型TMD系统的主体结构动力分析

2.1 顶部加装双向FPS型TMD系统的结构动力方程的建立

设主体结构为n层，每层具有2个侧向自由度，将FPS-TMD系统加装于该主体结构的顶部，变为2n+2个自由度系统，如图5所示。则该系统整体刚度矩阵由TMD线性刚度和主体结构刚度共同组成。

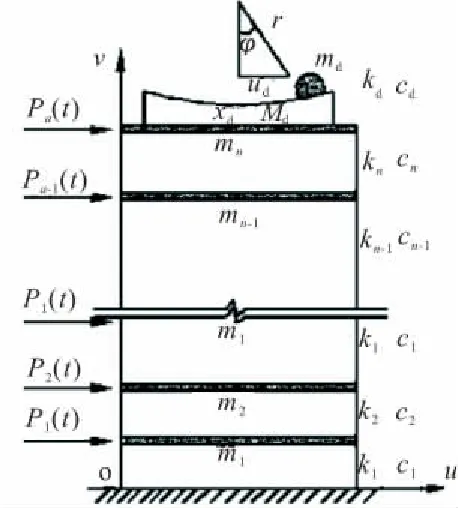
图5 主体结构顶部带双向FPS型TMD系统

其运动方程表示为：

(22)

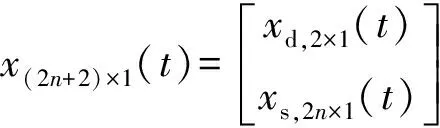
2.2 顶部加装双向FPS型TMD系统的结构动力方程的求解

利用状态空间法求解运动方程(22)，转换成连续时间系统下之状态空间方程式：

(23)

则在离散周期Δt下，离散时间系统状态空间方程式的离散解为：

(24)

式中：Ad,2(2n+2)×2(2n+2)=EAΔt为离散时间系统矩阵；Bd,2(2n+2)×2=A-1(Ad-I)Bc为离散时间摩擦力与部分恢复力配置矩阵；Ed,2(2n+2)×2=A-1(Ad-I)E为离散时间荷载配置矩阵；对于质量块与滑道之间摩擦力，在滑动状态时滑动面之摩擦力即为最大静摩擦力，但FPS-TMD的相对速度为未知值；而在非滑动状态时，滑动面之摩擦力未知，但TMD相对速度可以从动力方程求出。

3 自适应基因遗传算法

为使高层建筑顶部带FPS-TMD被动控制系统的性能达到最优，本文采用改进的自适应基因遗传算法，对其顶部设置带双向摩擦摆TMD系统的高层建筑，进行风振控制条件下的系统参数(包括两个方向的滑道半径、滑道与TMD质量块之间的摩擦系数)最优化设计，利用精英保存策略、自适应交叉和变异算子，以及自适应罚函数处理对基本基因遗传算法进行相应的改进。

3.1 精英保存策略

为了防止最优解在迭代过程中丢失和破坏，本文采用精英保存策略进行处理。即若当前找到的群体中某个体的适应度值比进化至目前出现的最好个体的适应度值还要好，此时就保留进化到目前最好的个体；反之则就找到当前最差的个体，然后用进化至目前出现的最好个体直接替换找到的最差个体，完成保存策略。

3.2 自适应交叉和变异算子

基本基因遗传算法中所采用的交叉概率Pc和变异概率Pm为定值，在优化过程中不变化。因此对于多变量的优化问题，搜索效率往往并不高，容易陷入局部收敛，从而造成“早熟”的结果。本文采取自适应交叉和变异算子的相关算法，使其根据个体适应度值与种群的最小适应度、平均适应度和最大适应度之间的相互关系，来动态调整交叉和变异概率。从而在整个优化过程中能够保证局部和全局搜索能力并重。达到既能在确定包含最优解的区域后收敛于最优解，又能在全局最优解的搜索过程中探索新的解空间区域。其中交叉概率Pc和变异概率Pm按如下公式进行调整[5]：

(25)

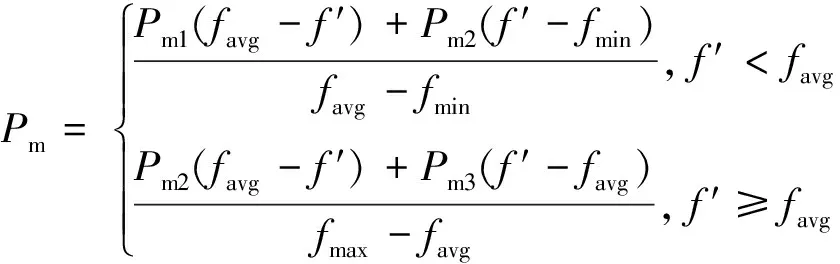
(26)

式中：f′，favg,fmin,fmax分别为个体适应度、种群的平均适应度、种群的最小适应度、种群的最大适应度。

3.3 自适应罚函数

为考虑各类约束条件对优化过程求解的影响，本文采取自适应罚函数来处理优化过程中出现的非线性隐性约束问题。利用当前群体中可行解的比例来衡量约束条件的违反程度，从而使得在优化过程中惩罚项准确发挥作用而不会发生惩罚项过大或过小的情况。与其他罚函数比，它结构简单、参数少易于调整，且能够非常有效地处理各种约束优化问题，具有较强的稳定性。其具体形式如下：

fitness(x)=ranking(f(x)+C×G(x))

(27)

C(ρ)=10β(1-ρ)

(28)

式中：ranking()是一个基于排序的适应度分配函数[6]；f(x)为目标函数值；G(x)为个体x违反约束条件的程度；ρ为本次优化过程中当前群体可行解的比例；β>0是一个需要调整的常量参数，具体可取1～10之间的一个整数；很明显惩罚系数C是随种群可行解的比例变化而改变的，如果可行解比例大那么C值就小，反之C值则较大，可以看出本文的方法是动态的、自适应的，在优化过程中C值不会过大或过小[7]。

4 计算实例及风振控制优化模型

本部分以广州新电视塔为实例，假设将双向摩擦摆TMD系统置于结构主塔顶部用于风振控制，并采用自适应基因遗传算法，对其进行FPS-TMD系统的参数优化分析。广州塔建筑总高度600 m，其中主塔体高450 m，天线桅杆高150 m，由于广州新电视塔有限元模型的动力自由度数非常庞大(图6a)，因此对它采取简化、降阶处理，得到包含37个节点，每个节点含有5个自由度，分别是两个水平方向的平动(x,y)及三个方向的转动(θx,θy,θz)[8～10]，总共185个自由度的糖葫芦串模型，如图6b所示。

图6 广州新电视塔与简化模型

广州新电视塔简化模型的动力特性与原三维有限元模型对比如表1所示[10]。结果表明，简化模型的频率及振型与原三维模型在前6阶基本保持一致，且因高耸结构的风致响应以整体前几阶响应为主，因此采用简化模型进行广州新电视塔的风振分析是可靠的。

本文所输入的外部风荷载激励时程w(t)，是通过采用谐波叠加法，对广州新电视塔在90°风向角沿塔体高度竖向分布的顺风向风荷载进行了模拟，设定时间步长0.5 s，持续1024 s。而脉动风速谱采用沿高度变化的Von Karman谱，并结合快速傅立叶变换和谐波叠加法，进而得到沿结构高度分布的顺风向脉动风速时程，再依据风洞实验得到的风荷载体型系数把脉动风速转化成风荷载后输入结构体系中[8,9,11]。通过模拟得到100年和10年重现期设计风速对应的顺风向风荷载时程后，对上式(22)所示的动力方程组采用状态空间法求解。本文采用100年重现期风荷载进行主体结构顶部风致位移分析，10年重现期风荷载进行主体结构顶部风致加速度(舒适度)分析。

表1 简化模型与三维模型自振频率对比

通过模拟得到100年和10年重现期设计风速所对应的风荷载时程作用于简化模型中，以有或无FPS-TMD系统的主塔结构顶部双向合成位移(加速度)均方根之比最小为目标函数，利用自适应罚函数处理其层间位移约束(100年风荷载下求得)、顶层位移(100年风荷载下求得)和顶层加速度约束(10年风荷载下求得)，采用自适应基因遗传算法对本实例进行风振控制作用下的双向FPS-TMD系统参数优化分析，优化设计变量则取为双向FPS-TMD系统的滑道摩擦系数μk、两个方向的滑道半径Rx、Ry。

本文采用的层间最大位移与楼层高度之比e1(x)、顶层最大位移与楼层总高度之比e2(x)、顶层最大加速度e3(x)约束的限值分别为不大于1/500，1/500，0.25 m/s2。上述三个约束因为均是非线性隐性约束，采用一般优化方法较难处理。本文所采用的自适应基因遗传算法可以很好地解决此类问题。对应于上述三类约束的函数表达式G(x)如下所示：

G(x)=[e1(x)/(1/500)+e2(x)/(1/500)+e3(x)/0.25]

(29)

从上式可以看出G(x)为个体x违反约束的程度且其为一个无量纲值。目标函数的表达式如式(30),(31)所示。

式(30)，(31)分别为100，10年重现期设计风速对应的模拟风荷载作用于顶部时，有无设置双向FPS-TMD系统的主塔结构，其顶部合位移(加速度)均方根之比的目标函数。x、y分别为双向摩擦摆TMD所控制的两个方向。

(30)

(31)

5 双向摩擦摆TMD系统参数优化结果分析

以广州新电视塔为算例，以顶部有无设置FPS-TMD系统的主体结构顶部风致位移或风致加速度均方根之比最小为风振控制优化设计的目标函数，采用前述的改进自适应基因遗传算法，利用精英保存策略、自适应交叉和变异算子，以及自适应罚函数处理被控制系统的风致层间位移约束、顶层风致位移和顶层风致加速度响应约束条件。对其进行风振控制条件下的系统参数(包括两个方向的滑道半径、滑道与TMD质量块之间的摩擦系数)优化设计进行分析。

5.1 100年重现期风荷载作用下风振位移控制的双向摩擦摆TMD系统参数优化分析

在100年重现期设计风荷载作用下，假设将双向摩擦摆TMD系统置于广州新电视塔主塔顶部，采用上述自适应基因遗传算法对双向FPS-TMD系统的滑道摩擦系数μk、两个方向的滑道半径Rx，Ry进行参数优化分析。其中结构阻尼比ξ采用1.5%，TMD的质量Md与结构总体质量Ms之比取为1%，目标函数取式(30)。自适应基因遗传算法的部分设置如下：种群的数量pop_size为20个；最大代数max_gen为100代；编码方式为格雷编码，每个变量的格雷编码位数为8，总长度为24；Pc1，Pc2，Pc3，Pm1，Pm2，Pm3分别为0.8，0.6，0.3，0.12，0.08，0.03；β取为1.3。由此可以得到目标函数的迭代图如图7所示：

图7 风振位移控制目标函数的迭代图

从图7可以看出，风振位移控制目标函数最终迭代到第42次时收敛，其取值为0.563736。相应的滑道摩擦系数μk、两个方向的半径Rx，Ry值分别为0.0067，24.0588 m，16.8627 m。当目标函数取最优值所对应的上述三个参数时，双向摩擦摆TMD的风振位移控制减振效率高达43.6264%。优化过程中种群最优个体目标函数值与种群目标函数均值的差异较大，说明种群在迭代过程中基因库丰富，种群中个体差异性明显，目标函数未陷入局部收敛，体现出自适应基因遗传算法的优越性。

5.2 10年重现期风荷载作用下风振加速度控制的双向摩擦摆TMD系统参数优化分析

在10年重现期设计风荷载作用下，假设将双向摩擦摆TMD系统置于广州新电视塔主塔顶部，采用上述自适应基因遗传算法对双向FPS-TMD系统的滑道摩擦系数μk、两个方向的滑道半径Rx，Ry进行参数优化分析。其中结构阻尼比ξ为1.5%，TMD的质量md与结构总体质量ms之比取为1%，目标函数取式(31)。而自适应基因遗传算法的部分设置如下：种群的数量pop_size为20个；最大代数max_gen为100代；编码方式为格雷编码，每个变量的格雷编码位数为8，总长度为24；Pc1，Pc2，Pc3，Pm1，Pm2，Pm3分别为0.7，0.5，0.3，0.1，0.08，0.03；α为0.9。得到目标函数的迭代图如图8所示：

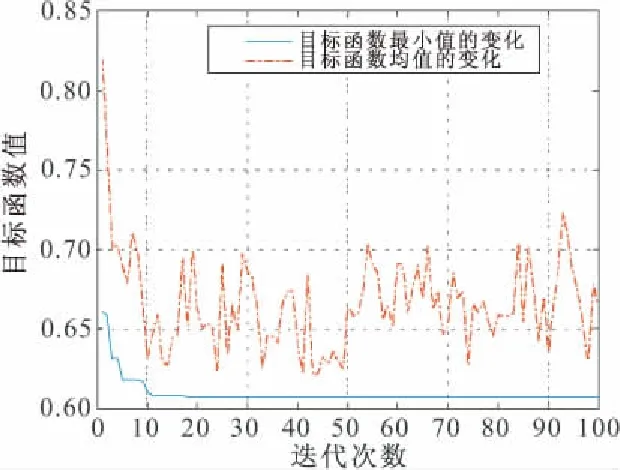
图8 风振加速度控制目标函数的迭代图

从图8可以看出风振加速度控制目标函数迭代到第18次时即收敛，其取值为0.607443。相应的摩擦系数μk、两个方向的半径Rx，Ry值分别为0.0035，21.0588 m，9.1176 m。当取目标函数最优值所对应的上述三个参数时，双向摩擦摆TMD的风振加速度控制减振效率达39.2557%。在迭代过程中，尽管迭代收敛速度快，但种群最优个体的目标函数值与种群的目标函数均值之间的差异较大，说明种群在迭代的过程中基因库丰富，种群中个体差异性明显，目标函数并未陷入局部收敛。从而反映出本算法的可行与优越的性能。

对比上述两种工况可知，在不同重现期设计风速对应的设计风荷载作用下，对于本算例采用的顶部FPS-TMD系统而言，风振位移控制和风振控制加速度目标函数的最优值是不同的，其所对应的双向摩擦摆TMD系统的优化参数值亦不同。当结构设计人员在进行高层建筑顶部设置FPS-TMD系统的风振控制初步设计时，很难取到一个比较好的值，如若利用本文的自适应基因遗传优化方法，可方便、快速而准确地得到双向摩擦摆TMD的最佳参数值，供设计使用。

6 结 论

双向摩擦摆TMD系统其造价低、易于维护且具有良好的自限、复位、摩擦耗能，安装于高层建筑或高耸结构顶部，不失为一种新型有效可行的减振方式。为使其风振控制减振效率尽可能达到最优，需对其系统的相关参数进行优化分析。本文所用的自适应基因遗传算法拥有强大的全局搜索能力，能够保证种群中优秀个体得以保存，同时又增强了种群的局部搜索能力，使目标函数顺利而准确地得到最优解，是一种有效可行的双向摩擦摆TMD系统参数优化方法，为设计人员初步设计提供了一种新的操作方便而准备可行的控制系统优化设计方案。