股线挤压效应对架空地线受力性能的影响

张 宇， 杨 繁， 曾 祥， 陈 波

(1. 国网江西省电力有限公司电力科学研究院， 江西 南昌 330096；2. 武汉理工大学 道路桥梁与结构工程湖北省重点实验室， 湖北 武汉 430070；3. 武汉博理建筑工程质量检测有限公司， 湖北 武汉 430223)

输电线路作为一种重要的电力基础设施，在国内外得到了广泛的应用。由于输电线路长期在野外服役，穿越很多地形和气候复杂地区，因此容易在强风、地震、覆冰等强烈外荷载作用下发生损伤和破坏，这将造成严重的经济损失和次生灾害[1～3]。据不完全统计，自建国以来我国输电线路已发生冰灾事故上千次[4～6]，强风灾变也有上千次。随着西电东送与超特高压输电工程的建设，越来越多的各类输电线路将被建造于地形和气候复杂地区。因此，结合我国输电线路工程灾变的实际，开展相应的防灾减灾和服役性能评估工作具有重要的科学意义和工程价值[7,8]。

架空地线是输电塔线体系中的重要组成部分，这也是输电塔线体系区别于其它各类高耸钢结构的本质特征。架空地线的力学性能和强度设计关系到输电线路的服役安全性，因此是输电线路设计建造中的一个关键问题。但常规输电线设计不考虑架空地线内不同层的力学性能，以往有关设计通常将架空地线视为各向同性的悬索，直接进行承载力分析。这种方法没有考虑架空地线中各股钢绞线的细部力学模型，不能考虑各股之间的相互挤压效应，无法掌握架空地线的细部受力特征[9]。基于此，本文研究了股线挤压效应对架空地线受力性能的影响；采用空间实体单元建立了架空地线的精细化有限元模型，并建立了地线精细化承载力分析方法和非线性迭代收敛准则；以南方某实际输电线路的架空地线为工程背景，研究了自重作用下地线的承载力特性并考察了不同地线参数对其承载力的影响。本文研究表明：架空地线的承载力具有较为显著的局部特性，各层股线的挤压对其承载力有一定程度的影响。

1 架空地线分析方法

架空地线由外层镀锌钢股线和内层钢芯组成，各层股线紧密缠绕在内层钢芯外侧，如图1所示。各层股线的力学性能将会在很大程度上影响架空地线整体的承载力性能。由于股线的长度和空间螺旋形态不同，因此各层地线之间将发生相互挤压和不协调变形，因此这将导致地线各股线之间发生内力重分配。

图1 架空地线构造示意

在进行架空地线钢芯的细部承载力特性分析之前，需确定地线的张力。在此基础上可将张力作为外荷载施加于架空地线精细有限元模型并求解不同层股线的内力。基于非线性有限元理论，可采用三节点索单元模拟具有强几何非线性特性的架空地线。架空地线是一种典型的大垂度悬索，只能承受拉力不能承受压力。可采用拉格朗日法建立架空地线局部坐标系，则地线单元上任意一点的位移可表示为[10]：

(1)

Ue=[uiviwi]Τ,i=1,2,...,n

(2)

(3)

通过建立不平衡张力和位移增量的关系可求得地线单元的切线刚度矩阵KT：

KT=KE+KD+KS

(4)

式中：KE为弹性刚度矩阵；KD为初位移刚度矩阵；KS为初应力刚度矩阵。

确定了地线的单元刚度矩阵后即可组集形成整体坐标系下的地线总刚度矩阵，可采用非线性迭代算法确定地线结构在外荷载作用下的张力。如需细致了解地线的承载力状况及细部应力分布，则需采用实体单元建立精细的架空地线承载力分析模型。通常可采用多用途8节点六面体单元来建立地线的精细化有限元模型，该实体单元中每个节点有3个自由度。单元应变向量ε可表示为：

ε=[∂]u=[∂]Nqe=Bqe

(5)

式中：u为位移向量；B为几何矩阵；[∂]为几何方程的算子矩阵；qe为单元节点位移向量。实体单元的刚度矩阵Ke及等效节点载荷矩阵Pe可表示为：

(6)

(7)

整体坐标系下可将所有单元的刚度矩阵和荷载向量进行组集形成整体刚度矩阵K和整体荷载向量P。自重作用下地线的受力方程可表示为：

Kx=G

(8)

式中：x为输电导线的位移响应；G为导线自重荷载。本文采用Newton-Raphson法和增量法相结合的方式对架空地线的平衡方程进行求解[11,12]。

2 架空地线有限元模型

本文以中国长江流域某山区输电塔线体系为工程背景进行了地线承载力分析研究。地线档距为300 m，地线型号为GJ-50，地线为两层共计7根股线，第二层为6根股线，地线每股直径为3 mm，地线总直径为9 mm，计算截面积为49.48 mm2，地线弹性模量为185 GPa，单位长度重量为411.9 kg/m，线膨胀系数为1.0×10-6/℃，绞线破断拉力为57.8 kN，对应拉断应力为1168 MPa。本文建立了地线局部截断的精细化有限元模型，如图2所示。该段模型长378 mm，包含了二层钢股线的三个完整的螺旋段。结构模型包含29590个节点，23364个三维实体单元，地线模型共有88770个自由度。沿地线轴线方向为x轴，横截面的两个正交方向为y轴和z轴向。各股线之间的摩擦系数μ取为0.20。图3为地线各股示意图。

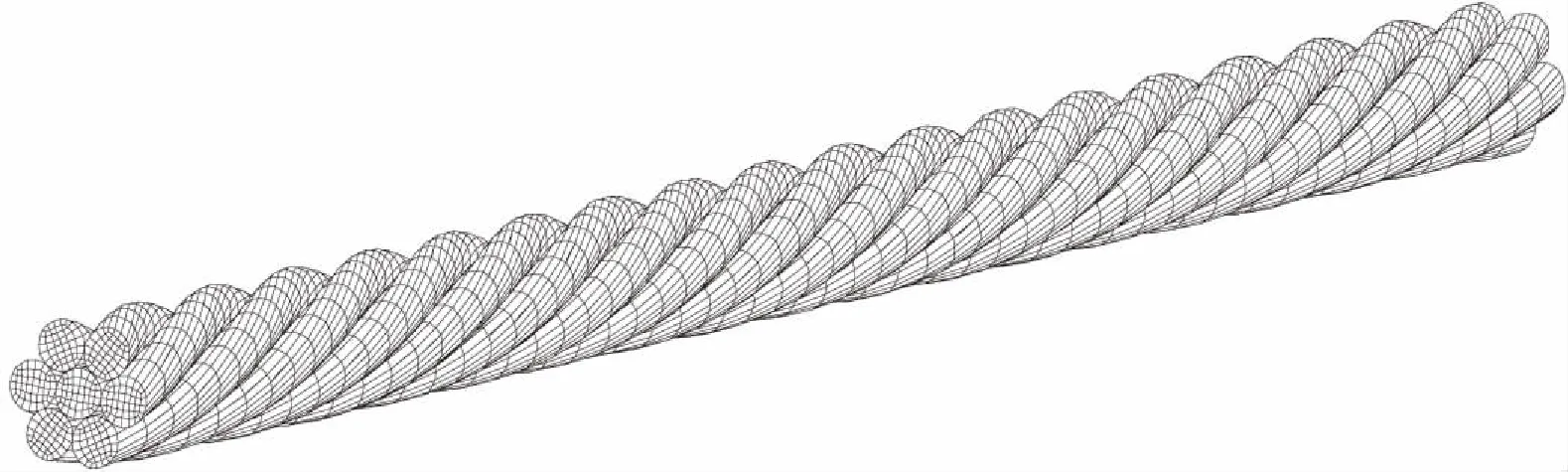
图2 架空地线有限元模型

图3 架空地线各股示意

3 架空地线承载力研究

基于前述建立的精细架空地线的分析模型，本文研究了内层钢芯自重作用下的承载力特性。图4显示了内层钢芯与外层股线截面平均轴应力的对比。由图中结果可知，由于内层钢芯和外层股线具有相同的材料特性和横截面积，因此两者的轴力较为接近，内层钢芯的轴力稍大于外层股线。而外层6根股线围绕内层钢芯基本对称缠绕，因此它们的轴力非常接近。类似的结论也可在轴应力的结果中得到体现。

图5显示了地线不同截面处的轴向应力云图，所选取的位置为所建模型的1/6和1/2截面。结果表明：对于地线而言不同股线的应力实际上存在一定程度的差异，即使对于同一根股线而言，在不同位置其应力也存在一定程度的差异。地线在受到轴向张力后，由于外层股线在轴力作用下将被拉长，因此其不可避免地将对内层钢芯产生挤压效应，同时外层各股线之间也会发生侧向的相互挤压。因此，在个股钢绞线相互接触处其轴向应力发生了一定程度的变化。

图4 地线各股不同位置的轴力和轴应力比较

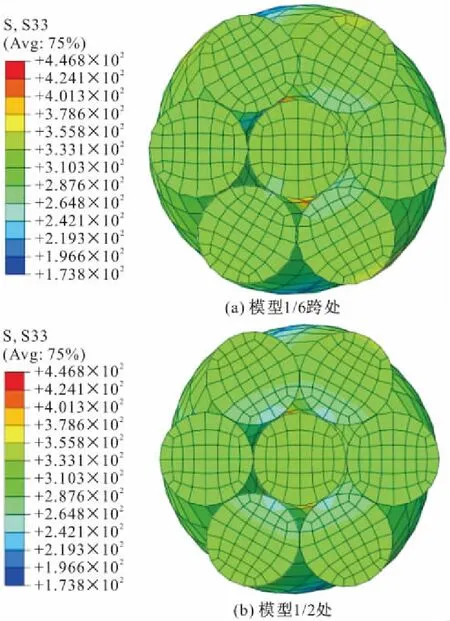
图5 地线不同截面的轴向应力云图/MPa

图6给出了内层钢芯轴应力云图，图7给出了内层钢芯和外层钢股线轴应力云图对比。由图6结果可知：内层钢芯由于受到外层股线的挤压，其轴应力在不同位置存在较大差异，其最大轴应力约为419 MPa，但是在接触挤压局部位置，其轴应力下降至270 MPa。显然内层钢芯的轴应力随着位置的不同存在明显差异，在地线性能评估中必须充分考虑各股钢绞线的细观挤压效应。类似的现象也可以在图7显示的内层钢芯与外层股线应力对比中发现。图7中第一张图显示的外层股线编号为part2-1，其最大最小轴应力分别为446 MPa和181 MPa。显然外层股线1的最小轴应力也发生在与内层钢芯发生挤压之处。由此可知，无论是对于内层钢芯还是外层股线而言，其轴应力峰值较为接近，但是由于股线挤压效应的影响，两者在少量局部区域的轴应力明显减小。

图6 内层钢芯轴应力云图/MPa

图7 内层钢芯和外层钢股线轴应力云图对比/MPa

4 参数研究

上述分析结论是在各股钢绞线摩擦系数为0.2时得到的。实际上由于材质的差异，钢绞线之间的摩擦系数将在一定范围内波动。因此本文在此针对摩擦系数进行了相应的参数研究。选取了0.15，0.20，0.25，0.30，0.35，0.40等6种典型的摩擦系数，考察了地线轴应力的变化特点，其结果如图8所示。图9给出了外层股线part2-1和part2-2的轴应力随着摩擦系数的变化结果。由图8结果可知：摩擦系数对轴应力有一定程度的影响，随着摩擦系数的增加，内层钢芯的轴应力逐渐缓慢增加，但增加幅度有限，并且在地线沿长度方向不同位置的增加幅度存在少量差异，在接触点处增幅稍稍大于非接触点处。

图8 不同摩擦系数下内层钢芯内力变化

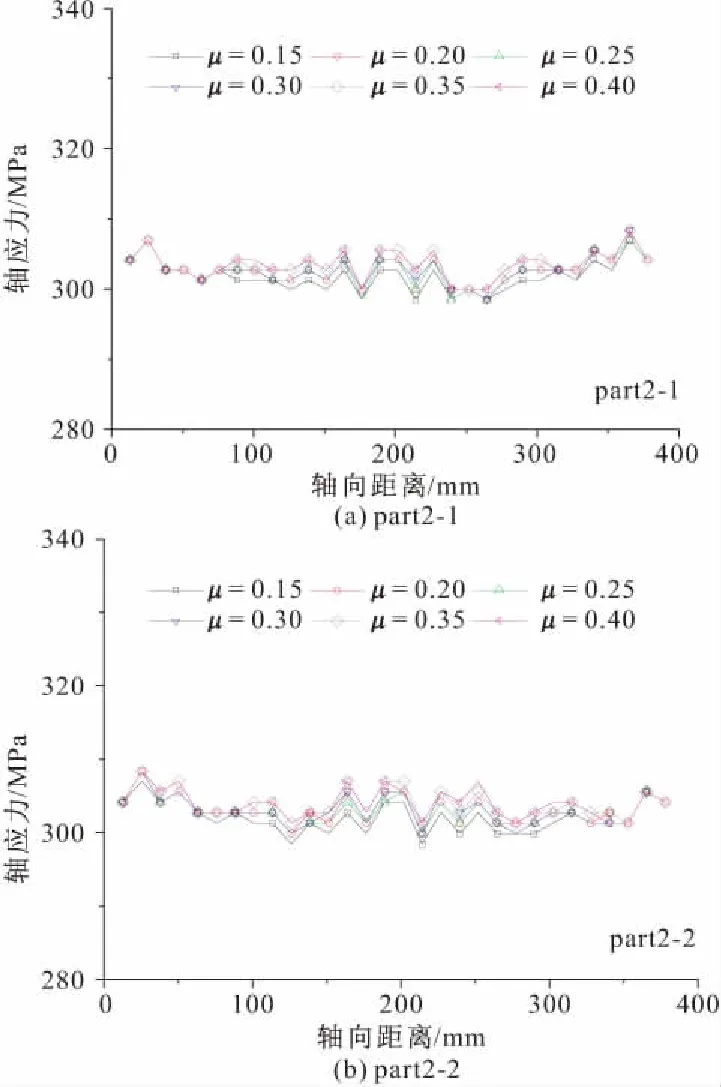
图9 不同摩擦系数下外层钢股轴应力变化

5 结 论

本文研究了股线挤压效应对架空地线受力性能的影响。采用多节点空间实体单元建立了地线的精细化有限元模型并建立了地线精细化承载力分析方法和迭代准则。以某实际架空地线为工程背景研究了自重作用下地线的承载力特性及其参数效应。本文研究表明：内层钢芯和外层股线具有相同的材料特性和横截面面积，两者的轴力较为接近，内层钢芯的轴力稍大于外层股线。外层股线各股的轴力非常接近。地线在受到轴向张力后，由于外层股线在轴力作用下将被拉长，因此其不可避免地将对内层钢芯产生挤压效应，同时外层各股线之间也会发生侧向的相互挤压。因此，在各股钢绞线相互接触处其轴向应力发生了一定程度的变化。架空地线的承载力具有较为显著的局部特性，各层股线的挤压对其承载力有一定程度的影响。