基于分位数的混合地理加权回归模型的商品住宅价格空间分析
——以哈尔滨市为例
石振武, 王 喆
(东北林业大学 土木工程学院, 黑龙江 哈尔滨 150040)
随着城市化进程的加快,房地产价格的空间协调发展问题,是房地产业乃至城市发展的关键问题。十九大提出房地产业要实现稳定发展,房价的稳定是主要因素,因此对房价的预测和分析具有重要意义。
当前研究房价的方法多是利用获得的数据结合地理位置,地理位置间的邻近关系会使得数据具有空间特性[1],为了将数据的空间特性纳入回归模型中予以分析,英国地理学家Brunsdon引入了地理加权回归(Geographically Weighted Regression,GWR),探讨英国房价与楼地板面积的关系,研究结果证实地理加权回归模型较最小二乘线性回归(Ordinary Least Squares,OLS)更优[2],该方法备受国内外学者的亲睐。目前国内有许多学科的学者已将GWR模型引入到自身的学科之中加以研究。汤庆园等[3]研究发现地理加权回归分解成局部参数估计优于OLS提供的全局参数估计,它可以深刻地揭示出房价和空间影响因子之间的复杂关系,而且可视化工具可以用地图的形式更详细地呈现出城市房价的整体景观。分位数回归可以解释变量的分位数来得到被解释变量的条件分布的相应的分位数方程,主要研究非正态变量。王新刚等[4]以湖北省黄石市为例,运用最小二乘线性回归(OLS)发现,GWR和局部线性地理加权回归(Local Linear Geographically Weighted Regression, LLGWR)能更合理和准确地解释住房价格的空间变异,且LLGWR优于GWR。某些研究者将OLS结合GWR提出了混合性地理加权模型,同济大学覃文忠在混合加权地理回归模型中,利用OLS结合GWR分析了上海房价,证明了混合加权的优越性[5]。还有些作者采用分位数方法分析房价,程亚鹏[6]以保定市为例采用分位数分解方法分析房价变动的原因,研究发现商品住宅价格的空间差异主要是由住宅属性特征的跨度性较大引起的。许启发等[7]以Cupola函数刻画资产间非线性关联关系,建立Cupola-分位数回归方法。
上述研究有的考虑了分位数因素的跨度性,有的考虑了局部空间平滑性,都没有将两者结合起来。本文借鉴国内外文献[8~11]提出一种基于分位数的混合地理加权模型,以哈尔滨市二手商品住宅小区(以下简称为“商品住宅”)为研究对象。哈尔滨市作为黑龙江省的省会城市,城区改造与开发并存。目前,全国二线城市房地产市场交易活跃,政府为禁止捂盘惜售出台了一系列政策。哈尔滨市区域分异特征显著,作为代表城市研究。为进一步明确哈尔滨市商品住宅价格影响机理,以期深刻理解都市冰城商品住宅市场空间异质性的驱动机理,从方法和实践上充实房地产经济学的研究案例,同时可为类似地区房地产管理工作提供有益借鉴。
1 研究区概况与数据获取
商品住宅是空间位置中极具固定性的产品,区位因素在空间中分布极不均衡,导致其对商品住宅价格的影响具有跨度飞跃性,同时群体中逐个个体的差异性构成了商品住宅的空间异质性。基于已有文献,应用R语言结合ArcGis技术采用基于分位数的混合地理加权回归模型进行分析。本文以哈尔滨市三环内主城区为研究区域,该区域涵盖了哈尔滨市6个中心区,松北区、道里区、道外区、南岗区、香坊区、群力新区,这片区域是居民活动最为中心分布的区域,也是哈尔滨市集中成片的城市区域。数据来源于目前我国最大的房产交易网站安居客的最新消息,数据信息包含小区名称、地址、价格(元/m2)、竣工日期、经纬度坐标。以住宅小区在售的二手房平均售价为基准数据,剔除奇异数据得到1345个数据。ArcGiS分析底图采用百度地图,所收集的要素点采用POI(Point of Interest)中的进户年份、地铁站、高等学校、公园、购物中心、河流、快速路、三甲医院、中学,在ArcGis-map平台上对所收集的数据建立空间数据库,建立相应点图层。图1,2为建立的数据源分布点、POI分布点以及中位数位置信息。根据图1可以看出,数据源属于研究面域上的离散点分布,此模式聚焦在空间对象的位置分布信息,图2将位置关系、特征以及样本点和要素点的空间分布充分显示。
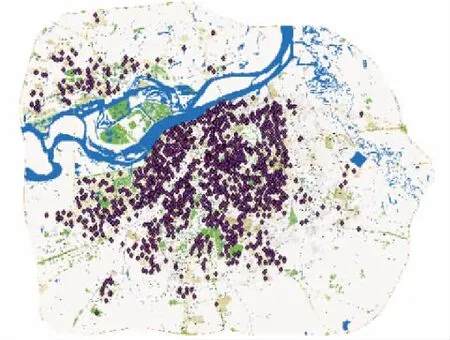
图1 哈尔滨市商品住宅
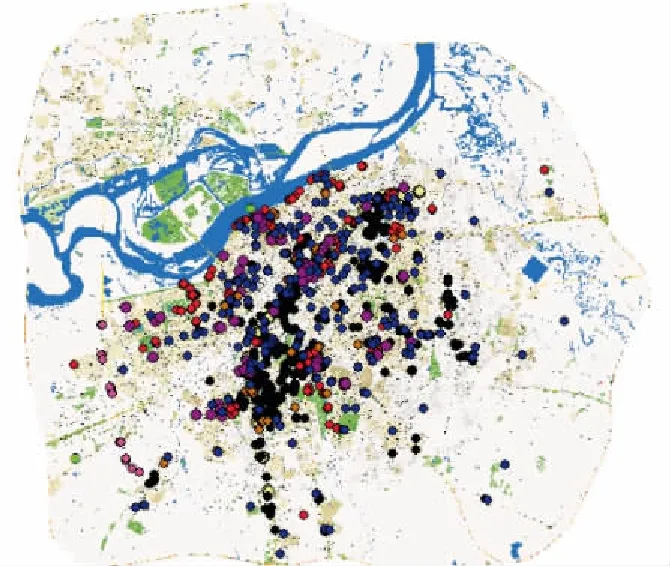
图2 要素点分布
2 研究方法
通过ArcGis软件得到的直方图(图3)和QQ-Plot图(图4)可知,商品住宅价格并不满足正态分布,有显著的异方差性,直接采用OLS或GWR都不能完全处理这种现象,因此对于这种异方差性的处理,选择分位数回归分析,分位数中核心体现数据聚合度的是中位数,所以本文采用中位数回归分析方法。
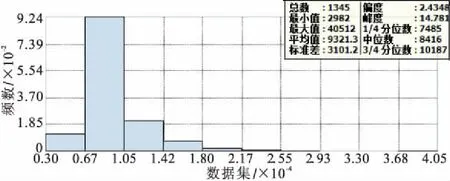
图3 商品住宅价格直方图
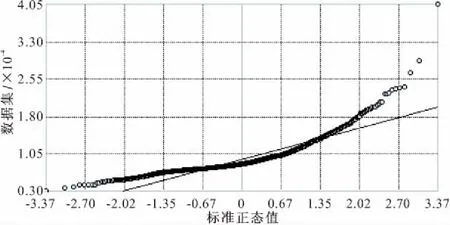
图4 QQ-plot图
2.1 分位数回归模型
设随机变量的分布函数为:
F(y)=Prob(Y≤y)
(1)
Y的τ分位数的定义为:
Q(τ)=inf{y:F(y)≥τ},0<τ<1
(2)
样本分位数回归是使加权误差绝对值之和最小,即
式(3)可等价为:
(4)
设u=Yi-ξ,一般地,τ分位数回归的损失函数为:
ρτ(u)=u(τ-I(u<0))
(5)
式中:I(Z)为示性函数,Z是指示关系式,代表u<0,u=0以及u>0。k个自变量可以得到参数估计值模型为:
(6)
通过式(6)得到其参数估计值,表示的参数意义为:当其他协变量保持不变时,这一估计差异来自一个连续型协变量的单位增量,或者虚拟变量值从0到1的变化。
分位数回归方程为:
(7)
2.2 基于分位数的混合地理加权回归模型(QGWR)
QGWR模型是同时考虑全局系数和局域系数的回归模型,全局系数即为常系数记为A,局域系数即为变系数记为B;对应的独立变量分两组分别记为Xa和Xb。由此MGWR模型为:
Y=XaA+XbB+θ
(8)
式中:Y是因变量矩阵;Xa是全局变量矩阵;A是全局系数矩阵;Xb是局域变量矩阵;B是局域系数矩阵;θ是残差。
本文提出一种基于分位数的混合地理加权回归模型(QGWR),将混合模型中的全局变量回归项引入分位数回归项,模型如下:
(9)

对于此模型的运算具体分为四步:(1)利用R语言对样本数据进行预处理;(2)对数据进行多元分位数回归判断不同参数的分位数结果;(3)对数据进行GWR回归;(4)通过结果分析筛选及剔除部分数据代入形成最终的分位数混合地理加权回归模型。
3 分位数混合地理加权性能分析
首先运用OLS方法进行全局模型估计。模型拟合度R2=0.61,F检验值为7.979693,其Prob(>F)为0.00<0.05,表明通过显著性水平为0.05的F检验,各回归系数与住房价格的线性关系显著。因样本数据空间分布的多重共线性,故构造异质数据去除变量的相关冗余性,以避免某些邻近样本点的多重共线造成的估计偏差。利用R语言对模型进行分位数回归得到图5,从图中可以看出各个变量与价格都不满足正态分布,存在偏差,本文通过对分位数的分析对数据进行二次处理,剔除影响因素小的变量,加大影响因素大的变量的权重,得到新的数据表,利用数据表得到分位数回归系数,带入本文所提出的回归模型式(9)中,得到的数据与传统GWR模型结果的对比如表1所示。AICc作为模型的显著性标识,从GWR模型中的23085.759532增加到25508.637895,远大于3,表明本文所提出的模型拟合度十分显著;拟合度R2由0.901015提高到0.926709,模型拟合性能强。
通过表2的估计系数对比可以看出基于分位数混合模型的关系强度和类型都发生改变,总体上看相关强度除了中学减少外都变大,说明本模型更能体现自变量和因变量之间的关系。产生这样的原因是混合加权地理回归模型的全局参数采用OLS中影响大的因素,本质上认为这些因素满足正态分布,但其实通过分析所有的因素,发现都有上尾和下尾的影响,分位数是考虑每个因素在不同分位时影响效应不同,通过对分位数回归的计算,找出对模型影响最大时相应因素的分位数回归系数替代全局系数,这样更接近实际情况。
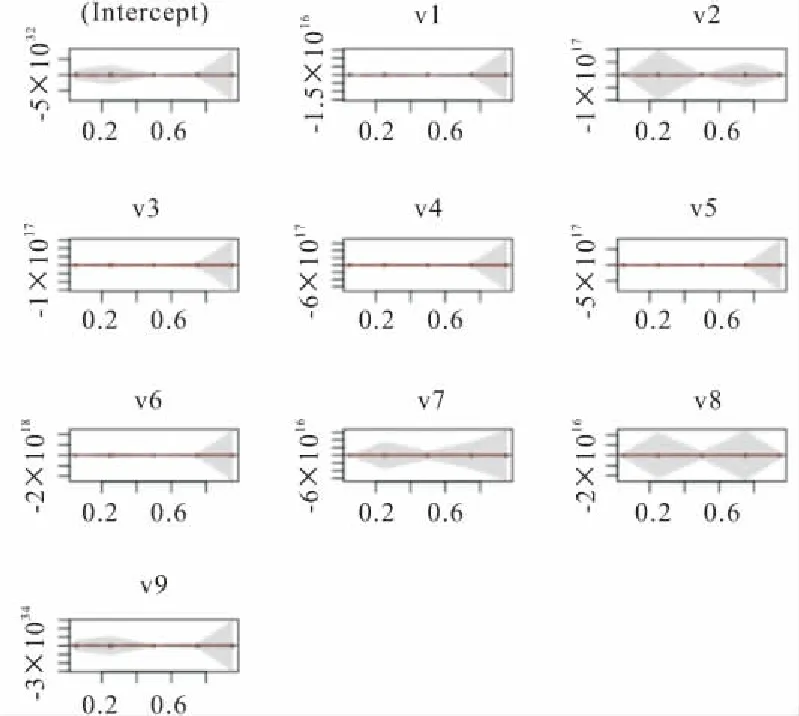
图5 分位数回归结果
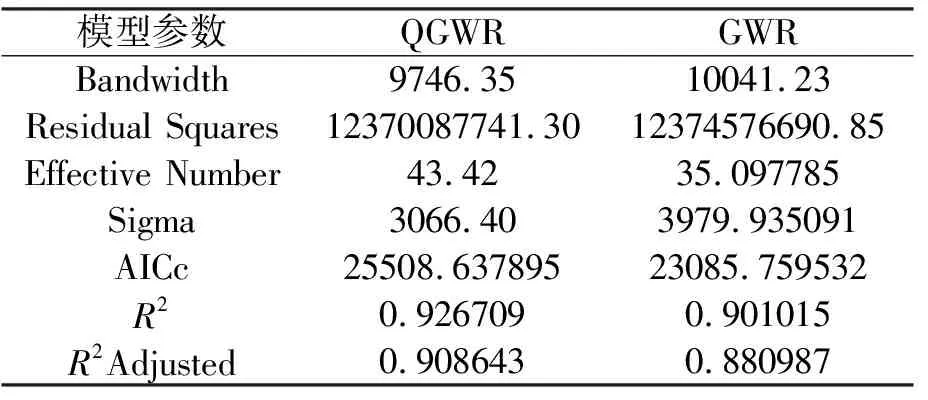
表1 哈尔滨市住宅价格GWR和混合GWR模型结果对比
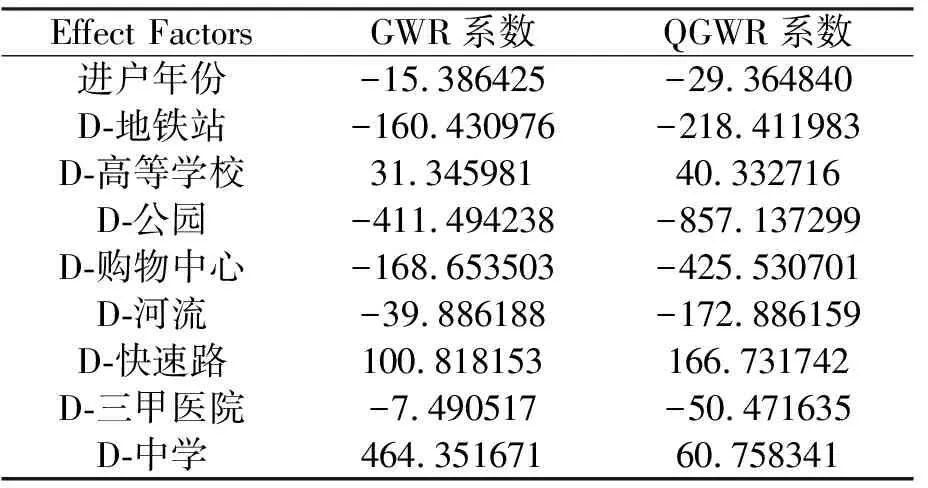
表2 GWR模型与基于分位数的混合GWR模型的估计系数
4 空间异质性分析
4.1 全局空间自相关分析
空间自相关的Moran’s I统计可表示为:
(10)
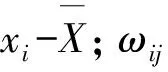
(11)
式中:E(I)=-1/(n-1)为其理论期望;V(I)=E(I2)-E(I)2是Moran指数的理论方差。
利用式(10)计算空间全局Moran’s I指数,进行最近距离分析,住宅价格空间数据需进行对数转换,以保证数据服从正态分布。以空间的1345个数据为基本数据源经对数转换后服从正态分布,大多数点都落在第一和第三象限。ArcGis空间自相关模块可以得到Moran’s I值和Z Score值。Moran’s I指数的值域为[-1,1],-1表示完全负相关,1表示完全正相关,取值为0表示不相关。如果Z Score值在[-1.96,1.96]区间外,那么返回的统计结果为可信;如果Z Score值大于1.96,表示样本点分布聚集;如果Z Score值小于-1.96,表示分布离散。计算结果见表3,I=0.604574>0,Z Score值得分23.388987,远大于99%置信区间双侧检验临界值1.96。表明哈尔滨市商品住宅价格在空间上呈现积聚状态,并存在一定的差异。由表4所示,得出商品住宅的最近邻指数NN比率为0.603727<1,NNZ检验值为-27.844016,在1%的显著性水平下通过检验。二者均表明哈尔滨市商品住宅价格在整体上存在空间正相关性,表现为样本点之间的聚集性较强,即样本点的距离越小,价格的差异越小。具体而言,分布在城市各区核心位置的商品住宅数,香坊区占总数的18.65%,南岗区占总数的25.78%,群力新区占总数的14.39%,道里区占总数的20.98%,道外区占总数的9.55%,其余分布在江北区域以及外围开发区。商品房具有明显的局部性和偏态,商品房高价格明显出现在新区和大型的商业区如群里与哈西,相近的城乡路房地产价格有明显的降低,松花江沿线江南地区价格远高于江北,并整体呈现集中程度由城市中心向外围开发区递减的趋势。

表3 Moran’s I指数

表4 最近邻指数
4.2 空间因素影响分析
样本数据特征表明,基于分位数的混合地理加权回归分析适合于90%哈尔滨市住房价格分析。图6是利用ArcGis统计分析模块中的趋势分析功能,生成哈尔滨市商品住宅价格的空间变化趋势图。哈尔滨住宅的空间格局是在南北两个方向上存在明显的中心俱乐部结构,哈尔滨市以中央大街、秋林、哈西万达为中心的单元结构发展到多元结构,松花江以南方向较以北地区房价明显升高,从侧面反应哈尔滨市的建设是由中心向四周辐射,局部地区形成了次中心,以哈西、群力新区崛起最为迅速。本节利用基于分位数混合地理加权模型得到上述九个自变量的系数,利用ArcGis软件将表2中的系数在地图中以影响因素形式用图6显示,图6表明哈尔滨市商品房价格空间变化趋势明显呈现局部性和偏态。

图6 哈尔滨市商品住宅价格趋势
采用近邻分析形成回归模型输入变量,其中进户年份直接作为变量输入,近邻采用住宅价格与地铁距离为500 m,采用与其余POI要素点距离为1 km。回归结果表明:哈尔滨市商品住宅价格可以由住房的本身属性、环境因素和区位属性来建模。
通过分位数回归模型的估计系数在哈市主城区影响分布图(图7),影响显著的点颜色排列顺序为:粉色>红色>蓝色,得到如下分析结果:

图7 空间因素对住宅价格影响显著的点分布
(1)商品住宅价格与进户年份成负相关,相关强度小,表明城市商品房价与房龄的关系不是太大,这与实际情况一致。
(2)与主城区地铁成负相关,相关强度大,但由于哈尔滨市地铁站数量较少,对整体影响显著性不强;从图7a可以看出,哈尔滨地铁的建设及开通,地铁1号线和地铁3号线已开通运营。交通便利度常被看作是影响住宅价格的重要因素,哈尔滨市早晚高峰期交通阻塞现象严重,由于哈尔滨市天气的特殊性,遇雪期时这种现象更加恶劣。因此居民往往选乘地铁,致哈尔滨市地铁沿线尤其是大直街和哈西地区的商品住宅价格普遍高于其他区位。
(3)与高等学校呈正相关,相关强度较低,这是由于哈尔滨高等学校附近的住宅建成年份较为久远,但在一定程度上在校教师对其购买力更高;从图7b可以看出,对高等学校附近的商品住宅价格有影响的地区,主要集中在江北大学城、学府路附近,此处均为高校密集区。
(4)与公园呈负相关,相关强度强,这是由于选定的公园点较多,从图7c可以看出,由于哈尔滨市的城市建设规划,公园集中在道里区、香坊区、群力新区、江北区,对这几处周边商品住宅价格的影响较为显著;而且大多进入商业区附近,对数据产生影响。
(5)与购物中心呈负相关,相关强度大;从图7d可以看出,商业购物点分布于各主城区中心,辐射范围较大,对整个主城区商品住宅价格均产生一定影响,距离商业购物中心近的住宅价格影响更大。
(6)与河流呈负相关,相关强度较小,这是由于哈尔滨市河流附近住宅样本数较少所引起;从图7e可以看出,哈尔滨市的江景房仅对河流沿线的群力新区有显著影响。
(7)与快速路呈正相关,相关强度较强,由于快速路建成在城市边缘,与实际相符;由图7f可以看出,快速路具有独特性,距离快速路入口的商品住宅价格有较大影响。
(8)与三甲医院呈负相关,相关系数较小;虽然分布系数有影响,从图7g可以看到,由于哈尔滨医科大学附属第一医院周围环绕远大购物、秋林等商业购物中心,因此其周边的商品住宅价格并不仅受医院这一单变量因素影响,其余三甲医院对周边的商品住宅价格影响较小。
(9)与中学呈正相关,相关系数较小,这是由于选取了所有的POI点,哈尔滨中学学区房的特殊性造成此数据不符合消费者观念,但与哈尔滨现状相符;从图7h可以看出,由于哈尔滨中学均分布在市中心,在分布图上可以看出此变量对住宅价格有影响,同时住宅价格还受其周边购物中心、火车站的影响。
5 结 论
本文以哈尔滨市主城区小区商品房为研究对象,提出了基于分位数的混合地理加权回归模型,由此得出以下结论:
(1)基于分位数的混合GWR模型的拟合结果表明哈尔滨市三环内主城区的商品房价格并非平稳,而与地理因素有关,商品住宅在空间上具有显著的空间异质性。模型更好地处理了非正态数据所带来的影响,从结果对比上来看要比传统GWR的性能优越。选取的商品住宅价格影响因素的9个变量存在显著的空间局部性和偏态性,导致价格出现偏差。研究区域化变量的空间属性时引入进户时间属性进行回归分析,模型具有很强的时空分析能力,结果表明时间因素的影响较小。
(2)模型对哈尔滨市商品住宅价格进行了空间计量分析,运行结果显示:哈尔滨市商品住宅价格呈明显的中心包围结构,并随距市中心距离的增加,商品住宅价格逐级呈圈层式递减;在哈尔滨市三环主城区以内对房价的众多影响因素中,以公园、购物中心、地铁影响力较大,表现出消费者对居住环境的舒适度、便利度以及生活质量上要求较多。
(3)商品房价格与整个城市的收入、国际国内金融环境、国家和地方政策及人们主观愿望都息息相关,如果回归更精确就应该考虑上述因素,学者可以在今后的研究中引入,值得深思。

