基于Hermite插值的制导炮弹姿态旋转矢量优化方法

邓志红， 汪进文， 尚剑宇， 张翔，2

(1.北京理工大学 自动化学院， 北京 100081； 2.中国兵器工业集团有限公司 西安电子工程研究所， 陕西 西安 710100)

0 引言

姿态测量是制导炮弹实现精确打击目标的一项关键技术，姿态测量的精度直接影响着炮弹制导的精度。因此，姿态解算算法分析和姿态测量系统设计便成为研究制导炮弹导航制导的重要环节[1]。目前，常用的姿态更新算法主要有欧拉角法、四元数法、方向余弦法和旋转矢量法[2]。针对具有高过载和高转速特点的制导炮弹，在弹丸飞行过程中，弹丸的空间角位置与旋转次序有关，在空间的有限转动具有不可交换性，通常采用等效旋转矢量优化算法对不可交换性误差进行补偿[3]。

在实际制导炮弹制导控制系统中，通常采用抗高过载角速率陀螺仪，其输出为角速率信息。国内外学者针对角速率输入下的捷联姿态算法提出了多种角增量提取方法：文献[4]针对高动态环境，引入规则进动，采用Newton-Cotes插值法进行角增量提取，但只给出了角增量提取公式，没有给出角增量提取过程；文献[5]采用Lagrange插值法对角增量进行提取，引入上一周期的角速率改进算法，算法精度随着子样数的增加而提升，但算法比较复杂；文献[6]提出单步长Newton后插法，但没有给出具体的角增量提取方案以及理论算法漂移；文献[7]给出了一种改进的三子样旋转矢量法，采用Lagrange插值法对角增量进行提取，可通过增加数值积分节点的方法来提高算法精度，但增加了算法复杂度；文献[8]提出了一种三次插值多项式的数值积分方法进行角增量提取，但没有进一步对算法漂移进行深入研究。因此，针对实际制导炮弹的角增量提取，如何降低算法复杂度、提高算法精度以及保证算法实时性，是迫切需要解决的问题。

角增量提取问题的核心就是一种高精度数值积分的构造。数值积分常见的有梯形公式和Simpson公式，它们的计算无需提供导数值，但代数精度不高[9]。吴新元[10]构造了一个高精度数值积分公式，但必须提供求积节点的1阶导数值，在角增量提取中不适用。Newton-Cotes求积公式的渐近性，可大大提高数值求积公式的代数精度，但同样必须提供n+1阶导数值[11]。因此，针对制导炮弹的姿态旋转矢量算法，寻求一种高精度的数值积分方法来解决角增量提取问题，变得十分迫切。

针对上述问题，本文在锥动环境下，提出一种基于Hermite插值法的角增量提取算法，并根据锥动环境下算法漂移最小的原理，优化Hermite插值算法，得出一组优化的角增量提取系数。对比Lagrange插值角增量提取算法，进一步推导各个角增量提取算法的算法漂移，针对不同的锥动频率、半锥角和姿态更新周期进行仿真对比。最后，通过仿真和实际测量数据验证，对Lagrange插值三子样算法、Hermite插值二子样算法以及优化Hermite插值二子样算法进行性能对比分析。

1 传统锥动环境下旋转矢量优化算法

为了更好地补偿刚体的不可交换性误差，常采用等效旋转矢量优化算法进行姿态解算，其核心为旋转矢量微分方程求解。对旋转矢量微分方程的求取，通常采用泰勒级数展开法进行求解，能够得到不同子样数下的求解结果，但对于高动态环境而言，其精度受限，因而需要对高动态环境下旋转矢量微分方程的求取进行研究。在实际应用中，锥动为最恶劣的工作环境条件，因此，本文以锥动环境为背景展开对旋转矢量提取算法的研究。

为了求取每一时刻的姿态更新矩阵，需要求取每一时刻的姿态旋转四元数，在更新之前，需要得到上一时刻弹体坐标系到下一时刻弹体坐标系的旋转矢量q，进一步需要得出等效旋转矢量Φ. 常用的近似旋转矢量微分方程[3]为

(1)

锥动是刚体运动的一种几何现象，当刚体受到环境振动或本身具有角运动，即刚体在两个正交轴方向存在频率相同而相位不同的角振动速率时，将导致刚体的第3个正交轴在空间绕其平均位置做锥面或近似锥面的运动[12]。

锥动环境下，弹体坐标系相对于参考坐标系的角速率[12]为

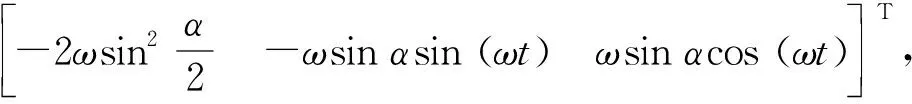
(2)

在锥动环境下旋转矢量算法的优化，主要是进行补偿项系数的优化，使得整个解算算法的漂移达到最小。

理论分析时，对(2)式进行角增量的提取，直接积分：

(3)

式中：i=1,2,…,n，n为子样数；h=tk+1-tk为姿态更新周期，k为第k次采样，k=1，2，…，n；t为开始采样的某个时刻。

针对(3)式进行角增量提取之后，不同子样数下的旋转矢量表达式为

(4)

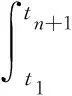
采用算法残留的直流误差作为算法的精度评估准则：

Φε(h)=|2q1-Φx|，

(5)

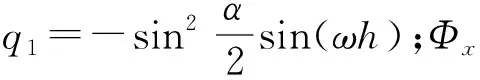
因此，Φε(h)越小，算法精度越高，从而可以得出单子样、二子样以及三子样的旋转矢量，如表1所示[3]。

表1 单子样和二子样及三子样优化算法

由表1不难看出，随着子样数的增加，算法的精度在提高，但算法的复杂度也在增加，从而降低了算法的实时性。因此，在实际应用中，需要权衡算法精度与实时性。此外，表1中的旋转矢量优化算法用角增量表示，但在实际应用中，角增量很难直接提取，通常采用数值积分方法进行提取，常用的数值积分方法是Lagrange插值[14]。

根据Lagrange插值积分公式，可得三子样角增量：

(6)

(7)

进一步可得三子样算法漂移为

(8)

将(6)式和(7)式代入表1中的三子样公式中，即为基于Lagrange插值三子样旋转矢量算法。

2 基于Hermite插值的角增量提取算法及其优化算法

对于制导炮弹，一般采用的是角速率陀螺仪，得出的是弹体角速率值，因此，针对这种角速率输入下的旋转矢量法，需要进行角增量的提取。为提高角增量提取精度，研究高精度的数值积分方法，引入Hermite插值积分，又根据算法的精度评估准则，使之最小，得出优化的Hermite插值积分公式。

2.1 基于Hermite插值的角增量提取算法

Hermite插值公式是区域上解析函数的Lagrange插值多项式的积分表示式。根据文献[15]中所构造的基于Hermite插值的高精度数值积分公式，可得只需计算求积节点函数值，无需提供求积节点导数值，求积公式如(9)式所示：

(9)

对于n子样算法，原理同Lagrange插值推导过程，将对应的时间节点以及陀螺角速率代入(9)式，可得

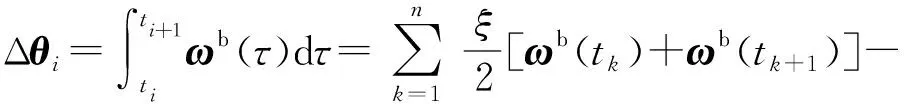
(10)

(11)

(12)

同理可得

(13)

(14)

将(13)式和(14)式代入表1中的二子样优化旋转矢量并联立(2)式，可得

(15)

根据算法的评估准则，将(15)式代入(5)式，可得基于Hermite插值的二子样算法漂移：

(16)

对比(16)式和(8)式，可得基于Hermite插值二子样算法漂移小于基于Lagrange插值三子样算法漂移，算法精度有明显的提高。

2.2 优化Hermite插值的角增量提取算法

虽然Hermite插值二子样算法的算法漂移相对于Lagrange插值三子样算法有一定的提高，但都处于同一个数量级，对提高姿态解算精度的效果不是很突显，且Hermite插值积分公式的角增量提取系数不能确保算法漂移最小。因此，需要对Hermite插值积分公式的系数进行优化处理，从而降低算法漂移，达到提高姿态解算精度的目的。

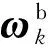
(17)

(18)

式中：k1和k2为待定优化系数。

将(17)式和(18)式代入表1中的二子样优化旋转矢量并联立(2)式，可得

(19)

根据算法的评估准则，将(19)式代入(5)式，可得基于Hermite插值的二子样算法漂移：

Φε=|2q1-Φx|=

(ωh)(2k1+k2)+

(20)

对(20)式中的三角函数作泰勒级数展开，并作同类项合并：

(21)

由于ωh≪1，为了尽量减少Φε，应该确保ωh的低幂次项为0，为此取

解得

将k1和k2代入(17)式和(18)式，可得优化Hermite插值二子样角增量提取算法：

(22)

(23)

将k1和k2代入(21)式，可得优化Hermite插值的二子样算法漂移为

(24)

对比(16)式和(24)式可知，优化Hermite插值二子样算法的算法漂移比Hermite插值二子样算法和Lagrange插值三子样算法的算法漂移小，算法精度有两个数量级的提升，为后续高精度的姿态解算奠定了良好的基础。

3 仿真实验结果与分析

本节分3步对算法效果进行分析和验证：首先进行算法漂移的仿真对比；然后在锥动环境下进行姿态角误差的仿真对比；最后，利用某型制导炮弹的试验数据进行验证，充分比较分析各个算法的优缺点。其中Lagrange插值三子样算法、Hermite插值二子样算法和优化Hermite插值二子样算法分别用L3算法、H2算法和Hopt算法表述，且各算法的漂移分别对应为Φε1、Φε2和Φε3.

3.1 算法漂移仿真结果与分析

由(8)式、(16)式和(20)式可知，算法漂移主要受锥动频率、半锥角和姿态更新周期影响，为了更加直观地得出这3个要素对算法漂移的具体影响，分别对L3算法、H2算法和Hopt算法得到的算法漂移进行仿真对比，充分分析各个算法的适用范围及优缺点。

3.1.1 锥动频率对算法漂移的影响

根据实际情况以及经验值选择仿真条件，半锥角α=1°，采样周期Ts=5 ms，姿态更新周期h=20 ms，锥动频率f的变化范围为1～100 Hz，锥动角速度ω=2πfrad/s. 根据(8)式、(16)式和(20)式对算法漂移进行仿真，采用对数坐标系突显细节，仿真结果如图1所示。

由图1可知：在锥动频率f≤50 Hz时， Hopt算法的算法漂移比其他算法小，且小于一到两个数量级；在锥动频率f≤37 Hz时，H2算法的算法漂移比L3算法小；由于ω=2πfrad/s，则ω>1 rad/s，算法漂移中含有锥动频率的幂次乘积，随着锥动频率的增大，幂次越高的算法漂移越大，当f>37 Hz时，算法Hopt的算法漂移大于其他算法。综合考虑，实际制导炮弹锥动频率小于25 Hz，则Hopt算法的算法漂移整体小于其他算法，适用于实际高动态环境下制导炮弹的姿态解算。

3.1.2 半锥角对算法漂移的影响

仿真条件：锥动频率f=1 Hz，采样周期Ts=5 ms，姿态更新周期h=20 ms，半锥角α的变化范围为1°～20°，锥动角速度ω=2πfrad/s. 根据(8)式、(16)式和(20)式对算法漂移进行仿真，采用对数坐标系突显细节，仿真结果如图2所示。

由图2可知，在半锥角α≤10°时，Hopt算法的算法漂移明显小于其他算法，且Φε3<Φε2<Φε1；当半锥角α>10°时，3种算法的算法漂移很接近，但Hopt算法的算法漂移始终小于其他算法。此外，实际情况中，半锥角的范围一般小于10°，因而Hopt算法具有一定的实际应用价值。

3.1.3 姿态更新周期对算法漂移的影响

仿真条件：锥动频率f=1 Hz，半锥角α=1°，采样周期Ts=5 ms，锥动角速度ω=2πfrad/s，姿态更新周期h变化范围为5～100 ms. 根据(8)式、(16)式和(20)式对算法漂移进行仿真，采用对数坐标系突显细节，仿真结果如图3所示。

由图3可知，在姿态更新周期h变化范围为5～100 ms之内，Hopt算法的算法漂移整体小于其他算法，且随着姿态更新周期的增大，各算法之间的算法漂移差距越来越明显，并始终保持Φε3<Φε2<Φε1的趋势。综合考虑，在实际应用中，Hopt算法可降低姿态更新采样频率，降低对导航计算机的要求，具有一定的实际应用价值。

3.2 姿态角误差仿真结果与分析

为了更加直观地对比各算法的性能，以锥动为研究环境，并以锥动旋转四元数为真实姿态旋转四元数，解算出理论姿态角。以(2)式为角速率输入量，分别采用上述3种角增量提取算法进行姿态解算，用解算出来的姿态角与真实姿态角作差，得姿态角误差作为最终的输出量。

仿真条件：锥动频率f=1 Hz，半锥角α=1°，采样周期Ts=5 ms，姿态更新周期h=20 ms，锥动角速度ω=2πfrad/s，仿真时间t=60 s，仿真结果如图4所示。

由图4可知： H2算法和Hopt算法的姿态角误差很接近，没有明显差别；H2算法和Hopt算法相比于L3算法的姿态角误差在滚转轴和偏航轴上的体现效果明显，H2算法和Hopt算法明显优于L3算法，但对于俯仰轴的体现效果不明显。此外，仿真结果也验证说明了锥动环境对俯仰轴的影响较大。3种算法间姿态角误差对比如表2所示，俯仰轴选取60 s处的角误差，滚转轴和偏航轴的角误差选取正弦波的极大值。

由表2可以直观看出，Hopt算法的整体效果优于其他算法。

为了更好地体现算法在高动态环境下的应用效果，将锥动频率提高至f=10 Hz，其他仿真条件及思路不变，可得仿真结果如图5所示。由图5可知，在高动态环境下， Hopt算法的姿态角误差随着时间发散的趋势小于其他算法，且H2算法比L3算法的姿态角误差小，说明H2算法和Hopt算法优于L3算法。具体的3种算法间姿态角误差对比如表3所示，俯仰轴选取60 s处的角误差，滚转轴和偏航轴选取60 s附近的峰值作为姿态角误差。

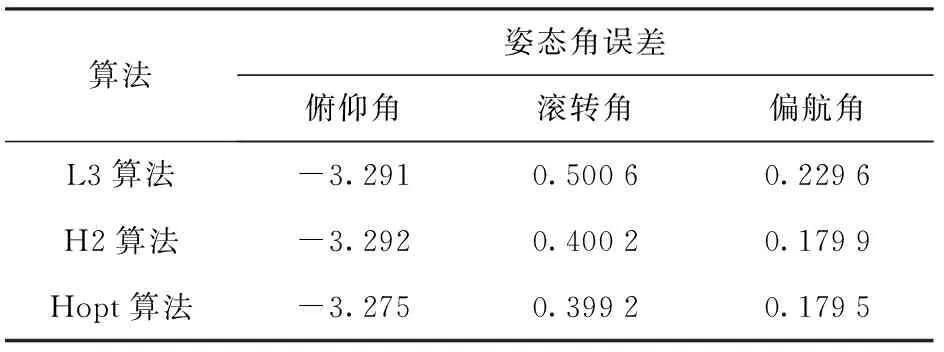
表2 f=1 Hz时姿态角误差仿真结果对比

表3 f=10 Hz时姿态角误差仿真结果对比

由表3可知：一方面，随着锥动频率的提升，姿态角误差也随着增大，这与3.1节中的算法漂移仿真结果相对应；另一方面，就俯仰角误差而言，Hopt算法明显优于其他算法，相比于L3算法姿态解算精度提升40.3%，相比于H2算法姿态解算精度提升24.0%.

综合上述仿真结果可知：锥动环境下，算法漂移趋势与理论研究是一致的；另一方面，整体而言，Hopt算法和H2算法优于L3算法，且Hopt算法在H2算法的基础上只改变了插值积分角增量的系数，没有增加算法的复杂度，仿真结果表明Hopt算法优于H2算法。

3.3 姿态角误差试验结果与分析

引入某弹实际试验数据，对各算法的性能进行验证。实弹试验以磁阻传感器和陀螺仪组合解算的姿态角作为真实值，以陀螺仪输出的角速率作为算法的角速率输入，利用3种角增量提取算法对该角速率进行处理，提取角增量，完成姿态解算。将解算出的姿态角与真实值作差，得出姿态角误差作为最终的输出量，进行定性分析。由于高动态环境下弹丸高速旋转，其滚转角变化迅速，本文利用弹载陀螺输出试验数据解算出的滚转角不具有实际价值，故不作考虑，可忽略。

试验条件：采样周期Ts=5 ms，姿态更新周期h=20 ms. 初始姿态角为：俯仰角29.46°、滚转角175.32°和俯仰角15.97°. 如图6所示为某弹的真实姿态角。

由图6可知，在弹丸发射后，25 s之前为上升阶段，弹体不稳定，且滚转轴转动较快，当俯仰角为负数之后，炮弹进入下降瞄准阶段，偏航角进行调整锁定目标。此外，由图6亦可知，实际弹丸的运动比锥动环境更复杂，可能含有规则进动、一般角速率运动以及随机角振动，因此仿真结果与试验结果存在一定的区别，但就整体趋势而言，仿真结果与试验结果存在一定的共性。

分别采用L3算法、H2算法和Hopt算法对角增量进行提取，完成姿态解算，与图6真实值作差运算，得出姿态角误差如图7所示。

由图7可知，对于俯仰角和偏航角而言，H2算法和Hopt算法的姿态角误差小于L3算法。具体的3种算法间姿态角误差对比如表4所示，俯仰轴和偏航轴姿态角误差选取末端处的角误差值。

表4 姿态角误差结果对比

由表4可知，从L3算法到Hopt算法，俯仰轴与偏航轴的姿态角误差呈现递减趋势，说明Hopt算法优于其他算法。具体对俯仰轴分析可知，Hopt算法明显优于其他算法，相比于L3算法姿态解算精度提升22.0%，相比于H2算法姿态解算精度提升6.7%.

综合算法漂移仿真、姿态角误差仿真和姿态角误差试验结果，不难得出，Hopt算法整体优于其他算法。

4 结论

本文就制导炮弹姿态解算过程中角增量提取精度不高的问题展开了研究，引入基于Hermite插值的高精度数值积分公式，设计了二子样角增量提取算法，并在此基础上提出了一种基于Hermite插值的制导炮弹姿态旋转矢量优化方法。仿真与试验结果表明：

1)Hermite插值二子样算法相比于Lagrange插值三子样算法，不仅算法漂移小，而且姿态解算更精确，说明本文引入的Hermite插值积分降低了旋转矢量算法的子样数，并极大地提高了算法精度，在实际应用中具有重大研究意义。

2)优化Hermite插值二子样算法相比于Hermite插值二子样算法的姿态解算精度有一定的提高，更重要的是优化Hermite插值二子样算法可降低姿态更新采样频率，降低了对导航计算机的要求，且适合高动态环境，具有很强的实际应用价值。