基于地磁辅助的弹载两轴陀螺传感器校正方法研究

鞠潭， 于纪言， 王晓鸣， 顾晓辉

(南京理工大学 智能弹药技术国防重点学科实验室， 江苏 南京 210094)

0 引言

陀螺传感器不仅能够测量物体角速率并解算物体姿态，而且具有小体积、低能耗、低成本等特点。因此，陀螺传感器被应用于各个领域[1-4]。然而，由于外界环境的干扰，陀螺传感器存在一定的非正交误差、刻度因子误差和零偏，这些误差使陀螺传感器测量精度下降[5]。因此，为了获取高精度的角速率测量信息，需要对陀螺传感器进行校正处理。

一般而言，陀螺传感器无法实现自校正功能，需要外部信息辅助校正[6]。对于三轴陀螺传感器的校正，最常用的辅助校正方法有基于全球定位系统(GPS)的辅助校正、基于加速度计的辅助校正和基于地磁传感器的辅助校正。将GPS测量运动物体得到的位置和速度信息作为输入量，以物体的运动学和动力学方程作为状态量，采用滤波估计的方式实时校正陀螺传感器相关系数[7]，但是在静态环境中，该方法无法获得较好的校正结果。在基于加速度计或地磁传感器辅助校正陀罗传感器的方法中，利用同一时刻物体姿态相同的思想，建立相应的校正模型，可以解算得到陀螺传感器的相关校正系数[2,8]。

基于上述方法建立的陀螺传感器校正模型具有高维度、非线性等特点，解决这种高维度、非线性系统的常用方法有卡尔曼滤波(KF)模型和最小二乘(LS)模型[9]。这两种常见的方法都能较大程度地改善陀螺传感器的测量结果。针对陀螺传感器校正模型的高精度解算，Yong等[10]研究了基于罗德里格斯参数的非线性观测器解算方法，Kim等[11]研究了非线性高斯牛顿回归法。与常见的KF模型和LS模型相比，这两种方法可以获得更高的解算结果。

上述研究只涉及陀螺传感器的三轴校正问题，但当陀螺传感器应用于低旋炮弹的姿态测量时，陀螺传感器的量程远远小于弹丸的滚转速率，陀螺传感器无法测量弹丸x轴的角速率，仅能使用两轴陀螺传感器测量弹丸y轴和z轴的角速率。然而，两轴陀螺传感器的校正同样涉及与x轴相关的非正交误差项。由于弹丸x轴角速率远远大于弹丸y轴和z轴的角速率，该非正交误差项将较大程度地影响陀螺传感器的测量精度。与其他陀螺传感器的应用环境不同，低旋弹丸独特的运动特性给两轴陀螺传感器的校正带来了挑战。

针对弹载环境下两轴陀螺传感器的校正问题，本文研究了基于地磁辅助的方法来校正两轴陀螺传感器。结合弹丸的绕心运动方程，推导了两轴陀螺传感器测量误差模型。由地磁信号解算得到弹丸x轴滚转角速率，结合两轴陀螺传感器的测量值，运用线性LS模型和KF模型校正陀螺传感器。数值仿真验证了本文方法的可行性，分析了弹丸x轴角速率解算误差和陀螺传感器测量噪声对较正结果的影响。最后，通过搭建半实物仿真平台，模拟弹丸转动，验证了在弹载环境下两轴陀螺传感器的校正效果。

1 陀螺传感器测量误差模型

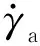
(1)

式中：t1、t2分别为地磁信号为0的两相邻时刻点。

(2)

由弹丸的绕心运动方程[12]可知，弹丸x轴的角速率ωx表示为

(3)

(4)

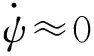
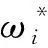
(5)

式中：ωi、ωj、ωl为弹丸三轴的真实角速率。由(4)式和(5)式可得到基于地磁辅助的两轴陀螺传感器角速率测量模型[5]为

(6)

2 陀螺传感器校正方法

在传感器的校正中，当已知弹丸角速率的真实值和测量值时，结合陀螺传感器的测量模型，就能求解出陀螺传感器的非正交误差、比例因子误差和偏差。本文研究了线性LS模型和KF模型求解两轴陀螺传感器相应校正参数的方法。

2.1 线性LS模型

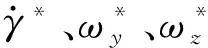
(7)

c=XR+N，

(8)

‖XLSR-c‖2=min ‖XR-c‖2，

(9)

式中：XLS为方程组的LS解。由(9)式将(8)式求解问题转化为线性LS问题。因此，可以得到方程组的LS解X0为

X0=cRT(RRT)-1.

(10)

由(10)式可得陀螺传感器校正的未知量。

2.2 KF模型

运用KF模型校正两轴陀螺传感器时，其第k个时刻的状态变量矩阵Xk为

Xk=[bxkyxsgykyzbykzxkzysgzbz]T.

(11)

由陀螺传感器常值误差假设可知，KF模型的状态方程为

Xk=Xk-1+wk-1.

(12)

zk=HkXk+uk+vk，

(13)

式中：

2.2.1 线性离散系统可观性判断

本文构建的KF模型属于线性离散系统，在求解状态变量矩阵Xk之前，需要研究线性离散系统的可观性。

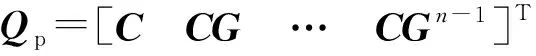
(14)

矩阵Qp的秩由ωxi、ωyi、ωzi决定，下面分两种情况分析矩阵Qp的秩：1)当ωx、ωy、ωz均恒定不变，即Hk1=Hk2=…=Hk9时，则rank(Qp)=3

2.2.2 KF模型更新方程

KF模型时间更新方程为

(15)

式中：P为X的协方差矩阵；Q为过程噪声方差矩阵。

KF模型测量更新方程为

(16)

式中：K为增益矩阵；R为测量噪声方差矩阵。

3 数值仿真

为了验证校正方法的可行性及各因素对该方法的影响，本文以某型尾翼稳定低旋弹丸为例。该弹丸x轴的角速率在50 rad/s附近，远远大于陀螺传感器的测量量程(<18 rad/s)。为了将两轴陀螺传感器应用于该弹丸的角速率测量中，必须对两轴陀螺传感器进行校正工作。

3.1 校正方法可行性分析

为了分析线性LS模型和KF模型校正两轴陀螺传感器的可行性，本文从陀螺传感器相关参数的校正结果、弹丸y轴与z轴角速率校正值和弹丸y轴角速率校正误差值3个方面进行研究。

仿真中取角速率陀螺测量误差的均值为0、方差为0.000 5 rad/s，陀螺传感器的轴间非正交误差(kyx、kyz、kzx、kzy)、各轴刻度因子误差(sgy、sgz)及各轴零偏(by、bz)设定值如表1所示。同时，表1中给出了线性LS模型和KF模型对各相关参数的校正结果。对比表1中设定值与两种方法的校正值可得，线性LS模型和KF模型得到的校正值与设定值十分相近，因此两种模型都能校正两轴陀螺传感器。

表1 两轴陀螺传感器相关参数设定值及两种模型校正值

为了更加直观地分析两种模型对两轴陀螺传感器的校正效果，通过下面方法还原弹丸角速率，得到弹丸角速率的真实值。在(6)式中，忽略各轴的测量噪声ni，可将(6)式简化为

(17)

由弹丸角速率的测量值M和陀螺相关参数的校正值A和B，可以得到弹丸角速率的校正值T的计算公式：

T=A-1(M-B).

(18)

由(18)式计算弹丸角速率的校正值T，图2中给出了弹丸y轴角速率校正值、真值与测量值的对比图，图3中给出了弹丸z轴角速率校正值、真值与测量值的对比图。由于弹丸低速滚转，随着弹丸滚转角的周期性变化，陀螺传感器y轴和z轴的测量量呈现出类正弦变化。同时，陀螺传感器y轴和z轴测量值的大小变化相同，仅相位相差π rad. 因此，在图2和图3中，y轴和z轴的校正量、真值和测量值看起来大体相同。在图2和图3中，经过LS模型和KF模型校正后，弹丸y轴和z轴的校正值与真值几乎重合。因此，LS模型和KF模型都能很好地校正两轴陀螺传感器。

为了进一步分析LS模型和KF模型对两轴陀螺传感器的校正效果，图4中给出了弹丸y轴角速率的校正误差和测量误差。在全弹道上，两轴陀螺传感器y轴角速率的测量误差均值为0.454 1 rad/s. 经LS模型和KF模型校正后，校正误差在0 rad/s附近。为了看清楚校正误差的局部细节，图4的子图中显示了弹道上2.0～3.0 s校正值误差的局部放大图。由图4的子图中可以看出，两轴陀螺传感器经过校正后，弹丸角速率的校正值误差在0.010 0 rad/s以内。从图4中可得，弹丸y轴的角速率测量误差从0.454 1 rad/s大幅降低到0.010 0 rad/s以内，因此LS模型和KF模型均能很好地校正两轴陀螺传感器。

3.2 影响因素分析

通过分析弹丸角速率的测量值M对弹丸y轴角速率校正误差的影响可知，当弹丸x轴角速率测量误差在0.261 8 rad/s以内且当角速率陀螺测量误差在0.001 6 rad/s以内时，经过本文方法的校正后，弹丸y轴和z轴的校正误差在0.010 0 rad/s以内。

4 半实物仿真

为研究基于地磁辅助的两轴陀螺传感器校正方法在工程应用中的效果，本文进行了半实物仿真试验，试验现场如图7所示。智能手机(试验用机型为荣耀8)内部自带有陀螺传感器和地磁传感器，将手机作为弹上姿态探测传感器。三轴转台模拟弹丸3个方向的角运动，通过局域网连接手机版与电脑版数学仿真软件。在试验过程中，将手机自带传感器测量的实时数据上传到电脑，从而获取本文校正方法中所需的陀螺传感器和地磁传感器测量信息，将转台内部反馈信息作为弹丸姿态角速率真值。由线性LS模型和KF模型校正两轴陀螺传感器，通过对陀螺传感器相关参数校正值、弹丸z轴角速率校正值和弹丸z轴角速率校正误差3个方面进行研究，分析了两种模型在工程应用中的校正效果。

根据手机传感器测量数据和转台内部反馈数据，分别由线性LS模型和KF模型校正两轴陀螺传感器，求解得到的两轴陀螺传感器相关参数见表2. 对比表2中与y轴和z轴自相关的4个参数kyz、kzy、sgy、sgz，发现LS模型和KF模型计算得到的结果十分相近。在校正与y轴和z轴自相关的4个参数kyz、kzy、sgy、sgz时，两种方法具有较高的一致性。然而，弹丸x轴角速率与y、z两轴的角速率存在两个数量级的差距。这是因为校正方法的细微差别，与x轴相关的两个参数kyx、kzx和与零偏相关的两个参数by、bz存在一定的差距。

表2 两轴陀螺传感器相关参数校正值

在第3节数值仿真中，通过对比校正值与设定值，可以判断LS模型和KF模型解算陀螺相关参数的优劣。但是，在半实物仿真中，两轴陀螺传感器相关参数为未知量，没有统一标准对比两种模型校正陀螺传感器的优劣。为研究两种模型在工程应用中的校正效果，由(18)式计算弹丸角速率的校正值T. 弹丸z轴角速率校正值、真值和测量值如图8所示。在图8中，测量值与真值存在较大的差距。然而，通过LS模型和KF模型校正后，两组校正值与真值几乎重合。因此，在工程实际中，LS模型和KF模型均能有效校正两轴陀螺传感器，基于地磁辅助的两轴陀螺传感器校正方法可行。

为进一步分析LS模型和KF模型对两轴陀螺传感器的校正效果，由地磁测量信息解算得到的弹丸x轴角速率测量误差如图9所示，弹丸z轴角速率校正值误差和测量误差如图10所示。从图9中可知，弹丸x轴角速率解算误差在-0.8～0.8 rad/s之间。从图10中可知，由两轴陀螺传感器测量得到的弹丸z轴角速率误差在-0.30～-0.05 rad/s之间。从图10中2.0～3.0 s校正值误差子图可知，LS模型和KF模型的校正误差在-0.02～0.02 rad/s之间。在弹丸x轴角速率存在较大解算误差时，经本文方法校正后，两轴陀螺传感器的测量误差可以从-0.30～-0.05 rad/s的范围减小到-0.02～0.02 rad/s的范围内。因此基于地磁辅助的两轴陀螺传感器校正方法具有较好的校正效果。

5 结论

本文研究了基于地磁辅助的两轴陀螺传感器校正问题，建立了两轴陀螺传感器测量误差模型。由单轴地磁信号解算得到弹丸x轴角速率，解决因陀螺传感器量程有限而无法测量弹丸x轴滚转角速率的问题。研究由线性LS模型和KF模型计算两轴陀螺传感器相关参数的校正方法。数值仿真验证线性LS模型和KF模型均能有效地校正两轴陀螺传感器。仿真分析弹丸x轴角速率解算误差和陀螺传感器测量噪声对校正结果的影响。通过半实物仿真，模拟弹丸角运动，验证了线性LS模型和KF模型的校正效果。试验结果表明：

1)当弹丸x轴角速率测量误差在0.261 8 rad/s以内并且当角速率陀螺测量误差在0.001 6 rad/s以内时，校正后弹丸y轴和z轴的校正误差在0.010 0 rad/s以内。

2)当弹丸x轴角速率解算误差在0.80 rad/s以内时，两种校正模型均能将陀螺传感器的测量误差从-0.30～-0.05 rad/s范围减小到-0.02～0.02 rad/s范围内。

数值仿真和半实物仿真证明：基于地磁辅助的两轴陀螺传感器校正方法具有较好的校正效果。