基于流固耦合方法的某风扇超声速非失速颤振研究

张 帅，陶 冶，高 磊，张霞妹

(中国飞行试验研究院 发动机所，陕西 西安 710089)

0 引 言

航空发动机的风扇/压气机转子工作在高压比、高转速、高负荷的级环境中，实际流动中存在风扇的长叶片与流体间强烈的耦合作用，这会引起叶片的气动弹性不稳定现象，严重时会导致发动机非包容性破坏[1]。因此，对风扇/压气机叶片的气动弹性响应预测和颤振产生及发展研究具有重要意义。发动机风扇/压气机中典型的颤振边界包括：亚/跨声速失速颤振、超声速失速颤振、超声速非失速颤振、堵塞颤振、弯扭耦合颤振、A100型颤振等类型[2]。

超声速非失速颤振通常发生在大型跨声速或超声速风扇/压气机上，典型特征就是发生颤振的叶片叶尖马赫数为超声速，是当今最引人关注的一种颤振现象[3-5]。这种颤振之所以引起人们的强烈关注，不仅仅是因为涡扇发动机的应用越来越广泛，更是因为这种颤振类型自身极其危险。D. G. Halliwell描述叶轮机械超声速非失速颤振两个典型特征：颤振边界随转速变化而快速变化、一般为突发型颤振[6]。

国内外针对叶轮机械中的叶片气动弹性问题的研究大多是通过流固耦合的分析方法来实现的。徐敏等[7]通过流固耦合的方法来预测叶轮机械的气动弹性稳定性。王征等[7]以简化后的某风扇转子为研究对象，对该风扇转子进行全通道的双向流固耦合数值模拟，研究其耦合前后气动及结构性能的变化情况，并通过模态耦合等方法求解转子叶片颤振问题，最终获取其颤振边界。

随着民用涡扇发动机的涵道比及风扇负荷的不断增加，风扇叶片的超声速非失速颤振问题日益突出。笔者将针对高转速下的风扇转子设计转速下近效率最高处的超声速非失速颤振问题展开研究。

1 叶轮机械颤振分析方法

能量法是目前叶轮机械叶片颤振分析方法中应用最广泛的一种，通过计算振动叶片表面非定常气动力在一个振动周期内对叶片所做的积累功，进而以气动力或气动阻尼系数作为系统颤振分析的衡量标准，这种方法一般能够较精确地对叶片的颤振现象进行预判。而通过流固耦合方法获得叶片表面的非定常气动力，不仅考虑到气动力对叶片的影响，还考虑到叶片变形对转子流场的影响，是一种比较接近实际流动的计算方法。

针对叶轮机械的超/跨声速非失速颤振问题，采用基于流固耦合方法的能量累积法进行求解。目前，对于压气机叶片颤振问题的研究多以二维叶片算例为主，研究三维气动弹性问题研究较少，且大多数不直接涉及颤振边界问题研究。由于发动机中压气机内部流动具有强烈的三维效应，传统方法选取三维模型的典型特征截面进行研究，这导致研究模型与三维流动实际状况的误差大，而按照三维问题进行研究就会更接近压气机内部的真实流动状况。

1.1 叶轮简化数学模型

由于流体计算软件中不存在移相周期性边界条件，在对叶片排的颤振问题进行数值模拟时，需进行多通道甚至全通道计算，这对计算资源提出了很高要求。为了简化叶片排的非定常计算，引入叶间相位角(Inter-Blade Phase Angle，简称IBPA)概念对叶片排的计算模型进行简化，这种简化方法可以大大减小三维问题非定常计算的计算量。

通过实验经验发现，当叶片振动时，叶轮机械上相邻叶片之间存在固定的相位差，而相位差的大小与叶轮机的颤振特性紧密相关。于是，Lane[8]提出了具有叶间相位角的颤振模型，该模型假定振动中所有叶片振动频率与幅值都相同，且相邻叶片间存在固定相位差。当整个叶轮机振动时，波动的叶片间貌似存在一种横波在叶片之间传播，这种横波被称为行波模型。因为叶轮机械的典型特征就是旋转对称性，可以通过行波模型简化叶片排计算模型，替代非定常计算中的多通道或是全通道计算模型。

假定叶排中的叶间相位角为σ，则叶排中每过2π/σ个叶片通道，叶片上下周期就会满足周期性条件，因而整个叶片排计算模型就可以缩减到2nπ/σ个叶片通道，其中n为大于等于1的正整数。叶片排的简化周期性边界如图1所示。

图1 叶栅周期性边界

通过移相周期性边界条件将叶片排的计算域进一步简化为单叶片通道。如图2所示，假设行波方向与叶片运动方向相反，进行移相后，在周期性边界条件上满足条件：

(1)

从式(1)看出，任何相位差σ均可应用于移相周期边界条件上。但在实际的叶轮中，叶片的数量是有限的，并非所有的IBPA都会出现。假定叶轮机械中有NBL个叶片，那么可能出现的叶间相位角为：

(2)

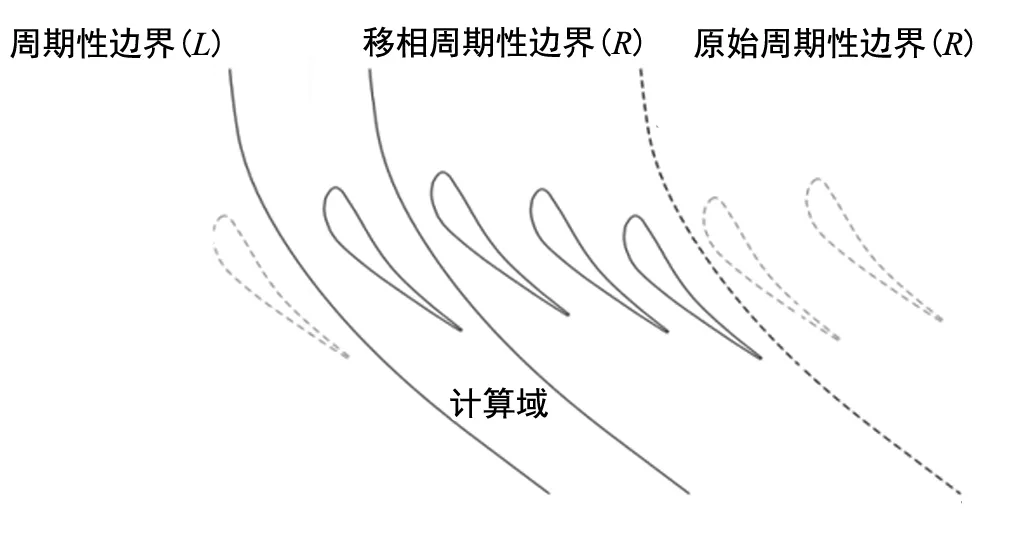
图2 叶栅移相周期性边界

1.2 能量法基本原理

能量法是属于解耦方法的一种。假设叶片发生振动，并以某一固有模态振型的形式，在其对应的固有频率下进行振动。然后通过计算叶片在一个振动周期内气动力对叶片的做功情况来判断能量的流动方向。若气流对叶片做正功，叶片在振动过程中从气流中源源不断地吸取能量，那么振动将可能趋于发散；当气流对叶片做负功时，气动力在振动过程中起到气动阻尼的作用，振动则趋于逐渐收敛。因此，可以通过定义气动阻尼系数来判断系统的稳定性。由于能量法将气动力的功作为判据，故将气动阻尼定义为与其相对应的负值。

=Aζ0πsin(φ)

(3)

对所得到的模态气动功进行傅里叶变换，得到一阶谐波。并对气动力系数无量纲化之后，定义气动阻尼系数(Aerodynamic Damping)。

(4)

(5)

(6)

当阻尼系数Ξ<0时，系统趋于不稳定；当阻尼系数Ξ>0时，系统趋于稳定。

1.3 基于流固耦合方法的振动模态耦合求解

在对叶轮机械的叶片耦合问题进行研究时，需要对其结构动力学方程进行求解。认为叶片在振动过程中是属于弹性形变的，因此采用振动模态对叶片结构的变形进行线性描述，假定其矢量位移为：

(7)

流固耦合问题的时域数值模拟过程中，流体域与固体域在交界面处的数据传递是非常重要的一步。由于在求解过程中，流体域网格与固体域网格在耦合交界面处完全不匹配，特别是流体域在叶片表面所生成的网格密度远大于固体域所生成的网格，这样就需选取一种数值插值方法来搭起流体域与固体域之间数值传递的桥梁。使用有限元方法计算叶片结构的模态振型之后，通过插值的方法将振型的变形后的坐标赋值于流体域的计算网格上。一般常用的数值插值方式有通用网格界面法(Generalized Grid Interface, GGI)与型函数法。

2 叶栅颤振特性分析与验证

2.1 叶栅算例简介

由于针对叶片结构特性测量的实验数据很少，针对三维叶片结构特性的实验数据更是无法获取。因此，选择二维叶栅Standard Test Configuration 4标准算例(简称STCF 4算例)作为验证能量法预测叶片颤振特性可靠性的算例[9]。图3是文献中实验所使用的试验装置实物图，在涡轮静子上共安装了20个根梢比为0.8的涡轮叶片，叶片通过弹性梁与轮毂间进行连接。在颤振试验中弹性梁发生弯曲，带动叶片发生振动，而其振动方向与叶片弦向的夹角为60.4°。

图3 STCF 4标准算例叶片实物图

取该叶片的50%叶高位置进行二维简化计算。在此叶片截面上，叶片的栅距为0.056 5 m，叶片弦长0.074 4 m，叶片安装角为56.65°，进口气流角与来流攻角在图中均已有表示。

2.2 STCF 4叶栅气动性能分析

对STCF 4叶栅的Case627实验状态进行定常状态下的气动性能研究。其中，进口气流角为-15.2°，进口总压为160 900 Pa，进口气流总温为288.15 K，进气攻角为41.45°，出口背压为100 700 Pa。

图4表示STCF 4叶栅在Case627实验状态下，叶片表面压力的数值计算结果与实验测量结果的对比图。从对比中发现，在此流动状态下，数值计算与实验测量的叶片表面压力值的分布不仅在变化趋势上相同，而且在数值上的分布也一致。

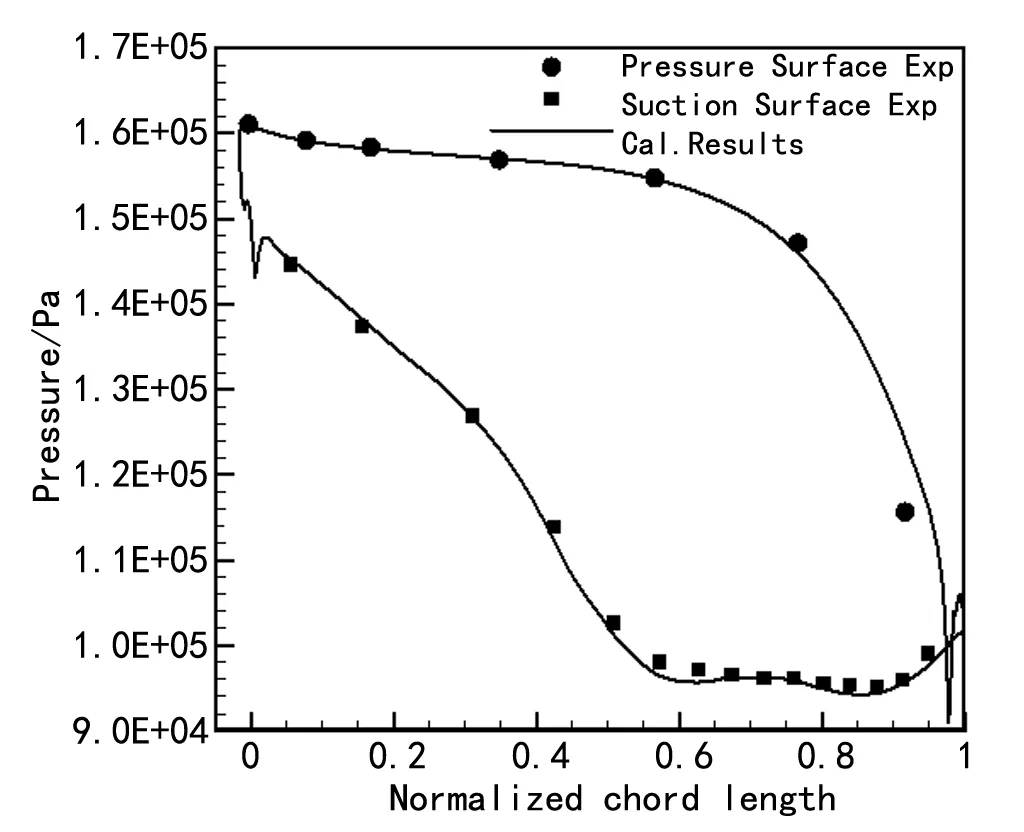
图4 STCF 4 Case627叶片表面压力分布对比

2.3 叶栅颤振特性分析

由STCF 4叶栅气动性能结果分析可知，叶栅Case627工况气动性能的实验值与数值计算值吻合较好。因此，基于Case627工况进行简化假设及非定常计算研究。图5所示为文献[10]中给出的STCF 4中的行波假设模型。

对叶片的运动位移进行简化，其运动方程为：

h=h0cos(ωt+nσ)

(8)

式中：h为叶片沿振动方向(与叶片弦向夹角60.4°)的位移值，h0=0.000 299 m为运动中的位移幅值；ω=936 rad/s为振动的圆频率；n为叶片编号；σ为叶间相位角IBPA。

图5 STCF 4中行波方向的定义

非定常气动力系数及气动阻尼系数定义为：

(9)

(10)

图6为Case627工况下，叶片的稳定区域(IBPA)数值计算与实验测量值的对比图。从对比图中分析发现，Case627中气动阻尼系数在分布趋势上吻合，对于叶栅弹性失稳区域的预测与实验数据基本一致。

图6 Case627工况下气动阻尼系数对比图

通过以上标准二维叶栅算例的计算分析，验证了基于流固耦合方法的能量累积法对于超/跨声速工况的颤振预测的正确性。对于下文复杂几何的三维转子叶片的颤振特性问题研究奠定了坚实基础。

3 某风扇转子超声速非失速颤振研究

图7所示为在进行风扇叶片颤振特性数值分析时所采取方法的流程示意图。

图7 叶片颤振分析流程图

其过程是先对固体结构进行结构动力学分析，分析预应力作用下的叶片模态振动状况，得到叶片的振型、自振频率等结构参数；再基于该转子以此阶模态振动的假设来进行非定常的流固耦合数值模拟；最后根据能量法计算叶片表面累积功或气动阻尼系数来判断其气动弹性稳定性。

选取该风扇转子在设计转速下的近效率最高点处的工况进行研究，此工况进口总压Pt=101,325 Pa、总温288.15 K，出口平均背压Pb=115 kPa。由叶轮机械转子叶片实验研究发现，转子叶片颤振受其前三阶模态影响较大，高阶模态由于其本身对应的叶片振动频率很高，而实际中叶片发生振动的频率较小且振动时幅值较大，所以文章主要对该风扇转子前三阶模态进行分析。

3.1 风扇转子计算模型简化

在进行风扇转子的颤振研究时，假定叶片以某阶模态按照前文假设的行波模型的方式进行简谐振动，则其关于位移的运动方程如下所示：

h=φζ=φζ0cos(ωt)

(11)

式中：h表示叶片表面位移矢量；φ表示振型的矢量；ζ=ζ0cos(ωt)为系统中模态的广义坐标；ζ0为广义坐标幅值；ω为振动圆频率。

定义风扇转子非定常模型的行波方向与叶片转动方向相反。为确定风扇转子叶片的颤振边界，先对转子叶片的前三阶模态振动的气动阻尼进行求解，来判断转子在各阶模态下是否出现负阻尼；然后针对出现负阻尼的不同模态状况，计算对应模态频率下叶片在各个IBPA的气动阻尼曲线；最后针对出现负阻尼对应的叶间相位角IBPA，改变叶片的振动频率，计算该模态及IBPA下的阻尼系数，通过插值方法得到气动阻尼零点，该点即为风扇转子对应模态下的超声速非失速颤振临界点。

3.2 风扇转子颤振特性分析

基于能量法理论，风扇转子对应的非定常气动力系数定义为：

(12)

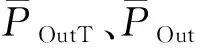
(13)

模态分析得到该转子叶片前三阶模态频率分别为189.34 Hz、599.32 Hz、967.69 Hz。图8所示为风扇转子叶片一阶振型表面非定常积累功率分布，气动力做功主要集中于叶片的上半部分。分析发现，当叶间相位角IBPA=120°时，叶片上半部分表面有较大面积的气流正功和负功区域，负功所占面积及强度较大，叶片发生颤振的可能性较小；当叶间相位角IBPA=334.3°时，叶片表面正功区面积及强度较大，其发生颤振可能性增加。将风扇叶片的一阶模态对应的气动阻尼系数随叶间相位角变化的关系绘制如图9，叶片在此阶模态振动时，气动阻尼系数在IBPA=334.3°附近出现负值，即出现颤振不稳定区域，这与叶片表面的能量分布分析相一致。

图8 转子一阶振型叶片表面非定常积累功率分布

图9 f=189.34 Hz一阶模态下叶片气动阻尼系数

该风扇转子叶片的第二阶、三阶模态对应的气动阻尼系数随IBPA变化的分布如图10、图11所示。分析发现，转子叶片的第二阶、三阶模态对应的气动阻尼系数均为正值，说明在此工况下，该转子叶片不会发生基于第二阶、三阶振动模态的颤振现象。

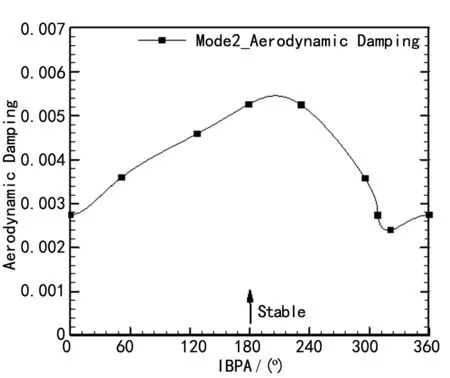
图10 f=599.32 Hz二阶模态下叶片气动阻尼系数

图11 f=967.69 Hz三阶模态下叶片气动阻尼系数

通过数值计算及分析发现，对于该风扇转子，一阶模态为其最危险的模态，并且其最危险的IBPA在334.3°附近。控制叶间相位角IBPA=334.3°不变，改变风扇转子叶片的振动频率，得到其不同叶片振动频率对应的气动阻尼系数，通过进一步处理得到转子的颤振临界点。

图12为一阶模态气动阻尼系数在临界点附近随叶片振动频率的变化图。依据线性插值的方法对气动阻尼系数零点进行插值，当气动阻尼系数为零时，其对应的叶片振动频率为f=201.68 Hz，即为一阶模态对应的超声速非失速颤振边界。对于该风扇转子而言，第一阶模态是其前三阶模态中最不稳定的模态，所以认定一阶模态颤振边界即为该风扇转子的颤振边界。从以上分析可知，当叶片的一阶模态频率低于f=201.68 Hz时，该风扇转子叶片会以一阶模态、IBPA=334.3°的形式发生超声速非失速颤振。

图12 IBPA=334.3°时一阶模态气动阻尼系数

4 结 论

采用基于流固耦合方法的能量累积法对某典型大尺度风扇转子的超声速非失速颤振特性进行了研究，得到以下主要结论：

(1) 风扇转子叶片在近效率最大点可能发生基于一阶模态、IBPA=334.3°的超声速非失速颤振，其边界的一阶叶片结构固有频率为f=201.68 Hz。

(2) 改变系统结构阻尼和材料阻尼等可提高叶片固有频率可达到避免发生超声速非失速颤振的目的。