齿轮传递误差与制造误差关联规律研究

唐健杰

(湖南农业大学，湖南 长沙 410128)

0 引 言

随着现代工业对齿轮要求的提高，齿轮受到了越来越多的关注。齿轮副的传递误差能够全面反映齿轮传动质量与动态特性[1]，许多学者在齿轮传递误差研究方面做了许多工作，Shuting Li[2]研究了制造误差、安装误差、轮齿修形对传递误差的影响，在文中他指出齿轮传递误差曲线的值会随着各项误差的增大而增大，其中制造误差还会改变传递误差曲线的形状，而安装误差与轮齿修形只改变齿轮误差传递曲线的值，不改变传递误差曲线的形状。Munro[3]提出了一种简单、精度高的计算直齿轮线外啮合所引起的传递误差计算公式，并使用实验结果对公式进行了验证。Rigaud, E[4]采用有限元方法，使用两种不同的三维单元，建立了考虑齿轮变形的齿轮有限元模型。分析得到了齿轮在准静态情况下的传递误差。然后对修形齿轮进行了分析，并将传递误差曲线与未修形得到的传递误差曲线进行了对比，证明恰当的修形可以减少传递误差的结论。李瑰贤[5]等人分别计算了齿轮副综合误差及弹性变形,并首次考虑误差影响因素的边界模糊性,把模糊数的概念引入到齿轮副静态传递误差的计算中,给出了模糊静态传递误差的计算方法。吴勇[6]将考虑传递误差影响的直齿轮副的扭转振动简化为一个自由度的变刚度系统。用平均值法并将参变方程转变为非参变方程后，得到其在静载作用下系统响应及其均值、方差的近似解析表达式。讨论了传递误差对响应均值、方差的影响。综上可见齿轮传递误差是齿轮研究中的一个重要的方面，目前给出传递误差与制造误差、及受载变形关联模型的文章很少，导致接近实际应用的齿轮动力学研究存在缺陷，笔者在唐进元提出的齿轮传递误差模型[7]基础上，考虑制造误差、受载变形等因素的选取，使用一对具体的齿轮进行传递误差的计算研究，将计算结果与齿轮箱设计分析软件Romax的计算结果进行对比，验证了模型的正确性，同时分析了制造误差对传递误差曲线的影响规律。

1 传递误差与齿轮制造误差、工作载荷的关联模型

唐进元在齿轮传递误差计算新模型[7]一文中，首先使用一对概念标准齿轮与一对实际齿轮建立了齿轮传递误差的概念模型。然后综合考虑齿轮的实际啮合情况，基于齿轮啮合的物理意义；建立了包含齿轮制造产生的齿距误差、齿形误差(考虑齿形的修形作用)，以及啮合过程中的轮齿弹性变形、接触变形的计算齿轮传递误差的力学模型。最后基于其所建立的齿轮传递误差的力学模型，推导出了计算齿轮传递误差的理论计算公式：

TE=Ef1+Ef2+ESAB-(DB1+DB2+DH1+

DH2)

(1)

式中：EF1、EF2为实际齿轮的齿形误差(包含修形量)；ESAB是当前啮合齿对与前一啮合齿对之间的综合齿距偏差；DB1、DB2为啮合点两轮齿沿啮合线的弯曲变形量，DH1、DH2为在啮合点两轮齿沿啮合线方向的接触变形量。

2 考虑齿轮制造误差与工作载荷的传递误差计算

2.1 齿轮制造误差的选取

齿轮的制造误差对齿轮的传动使用性能有着极其重要的影响，因此为了使所选用的齿轮能满足工作要求，必须合理选择齿轮的各项公差。按各项公差对使用性能的影响，齿轮每个等级的各项公差被分成三个公差组。制造过程中应根据齿轮的用途、工 作条件，在各个公差组中选用合适的精度等级。各公差组中的精度等级可以不同，但各组公差组之间是有紧密的联系的，所以各组的公差等级也不可能相差很大。

研究对象以某机械厂的一对直齿圆柱齿轮为原型；其精度等级为七级，主要参数及工作载荷如表1所示。为便于分析计算，现取小齿轮的齿廓偏差为零(即实际齿形偏向理想齿形的内部)；取小齿轮的齿距误差为按正弦分布的函数值，其分布函数为：

(2)

式中：z为齿轮的齿数；t为齿轮轮齿的编号，其取值范围为：t∈[1～z]。取大齿轮的齿廓偏差同为零，大齿轮的齿距误差的分布函数为：

(3)

齿轮结构如图1所示。

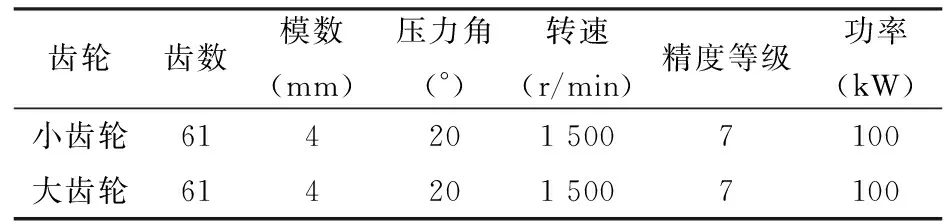
表1 齿轮参数及载荷参数

图1 齿轮啮合结构示意图

2.2 齿轮受载变形的规律

由于齿轮材料的柔性，轮齿在受载时会产生挠曲变形和接触变形[8]，综合表现为齿轮的啮合刚度。已有很多文献讨论了齿轮啮合时的变形规律[9]。使用载荷与Kuang, J.H.和Y.TYang[10]推导出来的刚度公式计算轮齿的接触变形和挠曲变形。单齿刚度公式Ki(ri)为：

(4)

式中：A0、A1、A2、A3为与齿数相关的系数。i=(p、g)，rp、rg分别为主、从动轮的基圆半径；Rp、Rg分别为主、从动轮的分度圆半径。X为变位系数，m为模数。

依据文献[11]，假设：①在实际啮合中忽略动态载荷对刚度的影响；②齿轮的各齿几何，物理特性一样。此时啮合点处综合刚度k(t)为：

(5)

齿轮在啮合过程中存在单双齿的交替，其中双齿啮合时间为(ε-1)×100%，理想状态下双齿啮合区啮合时间长度可以分为相等的两部分，这两部分中间既是单齿啮合区。因此可使用单齿啮合刚度叠加得到齿轮的啮合刚度；叠加部分的时间长度为(ε-1)×50%。按照上述公式，计算出例举齿轮对中齿轮啮合过程中的刚度曲线k(q)，如图2所示。在设定的功率下轮齿的弹性变形为：

DB1+DB2+DH1+DH2=δ=(fp/b)/k(q)

(6)

其曲线如图3所示。

图2 齿轮啮合刚度

2.3 基于齿轮制造误差与工作载荷的传递误差计算

由式(2)知齿轮的传递误差由制造误差与轮齿的受载变形所组成。以大小齿轮啮合处的一对轮齿为起始点(标定此时的传递误差为零)，分别标定大齿轮、小齿轮上的轮齿。则第k(取值范围为1～z)对轮齿参与啮合时的传递误差可记为：

DH1+DH2)

(7)

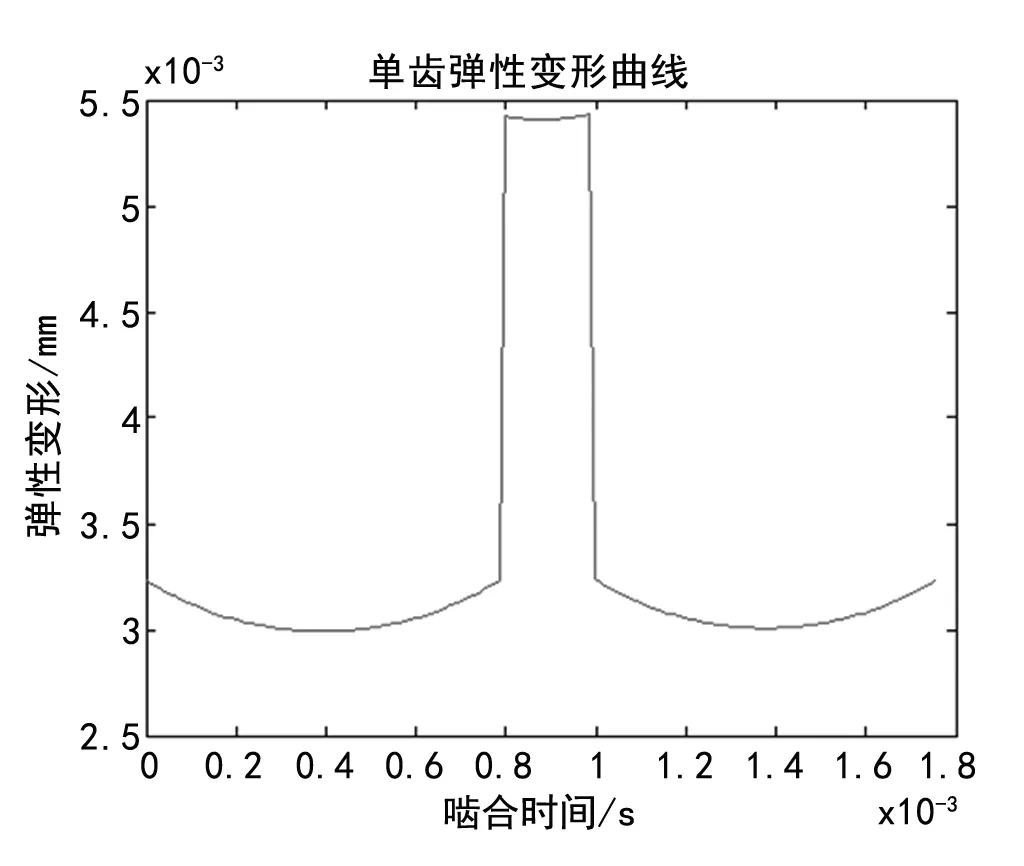
图3 单个轮齿在啮合过程中的变形曲线

在啮合过程中各对轮齿上的载荷历程相同，所以只需计算出啮合齿轮中一对轮齿的变形即可。按上述公式原则在MATLAB中编程计算出表1的啮合齿轮传递误差如图4所示。图4的横坐标为啮合齿对，纵坐标为传递误差(啮合线上的位移μm )。

图4 Romax计算得到的齿轮传递误差

2.4 传递误差计算与Romax计算结果的对比

Romax软件是一款专门进行齿轮设计分析的专业软件，将使用公式(1)计算所得的传递误差与Romax计算结果进行对比；如图5所示。由图可见两种计算结果的峰值为±52 μm，最大峰峰值均为100 μm，且两种传递误差曲线变化趋势基本上相同。但是使用新模型计算所得到得传递误差值与Romax计算得到的曲线相比， Romax软件计算得到的传递误差曲线中有许多尖点，并且在中间偏右有一部分曲线误差较大。误差的原因分析主要是因为在新模型中没有考虑到齿轮侧隙与偏载对齿轮传动的影响，当齿距误差较小且正负值变动时，由侧隙与偏载引起的传递误差被凸显出来；因此引起了传递误差曲线局部不符。但是总体上，与图4的对照表明我们提出的传递误差公式(1)的正确性。

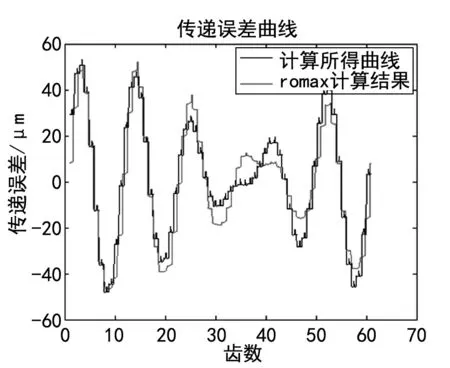
图5 传递误差对比

2.5 传递误差与制造误差推算分析

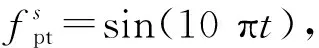
图6 传递误差曲线与制造误差关联图

4 结 论

使用提出的齿轮传递误差计算模型，给出变形与误差的具体计算公式，以一对齿轮传动为例，利用公式计算了传递误差，计算结果与Romax软件的计算结果进行对照，结果表明两种方法计算出的传递误差基本相同，并给出了制造误差对传递误差曲线的影响规律。研究给出的传递误差的计算模型与方法概念清晰、计算简单，通过传递误差与齿轮动力学方程的关联可实现制造误差、工作载荷等与动力学性能参数的耦合，为齿轮动力学研究基础性提供了相关基础条件。