高速机车走行部齿轮传动系统的动力学仿真

刘海娥, 张建国

(郑州铁路职业技术学院 机电工程系，河南 郑州 451460)

0 引 言

渐开线齿轮作为一种必不可少的连接和传动的通用零件, 广泛应用于机床、车辆、船舶及航空器等传动装置中。同时在机车传动领域也有着重要地位，作为整个传动装置的核心部分，传动齿轮使机车通过牵引电机电枢轴传递动力而使车轮转动，而齿轮又是最容易损坏的机械零件之一，齿轮传动机构的故障和失效将会对整个生产造成巨大的损失[1]。准确掌握齿轮传动的力学特性及运动特点，对于齿轮系统的可靠性设计、校核计算及故障诊断具有重要作用[2]。

1 高速机车走行部齿轮传动系统虚拟样机模型

虚拟样机仿真分析软件ADAMS(Automatic Dynamic Analysisof Mechanical Systems)是对机械系统的运动学与动力学进行仿真计算的软件，集建模、计算和后处理于一体。采用SolidWorks软件建立齿轮传动系统各零件的模型并进行装配，高速机车走行部齿轮传动参数如表1所示。装配设定达到要求后，将三维模型导入ADAMS，完整的齿轮传动系统虚拟样机模型如图1所示(为了更清楚地观察齿轮传动机构内部接触，对上箱体进行了隐藏)。

2 动力学模型仿真分析

某型机车走行部齿轮传动系统参数如表1所示。现假设电机转速400 rad/s，车轴负载2 584.3 N·m。

为在电机轴上施加转速时不出现突变，并模拟电机启动和关闭状态，使用STEP函数使转速在1.5 s内由0增加到400 rad/s；1.5～4.0 s保持匀速转动；4.0～5.0 s转速由400 rad/s减回0。即STEP(time，0.0，0.0，1.5，400)+STEP(time，1.5，0.0，4.0，0)+STEP(time，4.0，0.0，5.0，-400)，time为时间自变量。在车轴上施加负载2 584.3 N·m。

完成模型的定义之后，考虑到齿轮的转速较高，以及进行仿真操作耗时较长，所以设置仿真总时长为5 s，总步数为2 500步。首先进行正常状态仿真，用以验证试验的正确性，如图2所示。

表1 某型高速机车传动齿轮参数

图2 正常工况下两齿轮的加速度

在1.5～4 s的时间内，从动齿轮转速基本稳定在91.90 rad/s。则有实际平均传动比为：

与理论传动比4.35误差只有0.05%，可以忽略不计，满足传动比要求。同时验证了齿轮齿形和建模方法的正确性。

为了分析各种故障状态下齿轮的动力学表现，分别模拟了以下六种不同工况：

(1) 正常状态：以导入的正常模型进行仿真分析；

1.1.5 排除标准 非随机对照研究，患者为非慢性阻塞性肺疾病合并呼吸衰竭，对照组非无创正压通气治疗，两组常规治疗不一致，数据统计不完整，无有效数据提取，重复发表的研究，综述等。

(2) 齿轮偏心(径向跳动)：导入正常模型之后，主动齿轮轴线与电机轴轴线偏离10 mm，然后进行仿真分析；

(3) 传动轴偏斜：导入正常模型后，主动齿轮与电机轴旋转0.04 rad，然后进行仿真分析；

(4) 中心距误差：导入正常模型之后，主动齿轮与电机轴平移10 mm，然后进行仿真分析；

(5) 主动齿轮断齿：以导入的主动齿轮断齿模型进行仿真分析；

(6) 被动齿轮断齿：以导入的被动齿轮断齿模型进行仿真分析。

2.1 角速度曲线分析

通过ADAMS/View的后处理功能，可以得到仿真结果数据组成的曲线图，如图3所示。

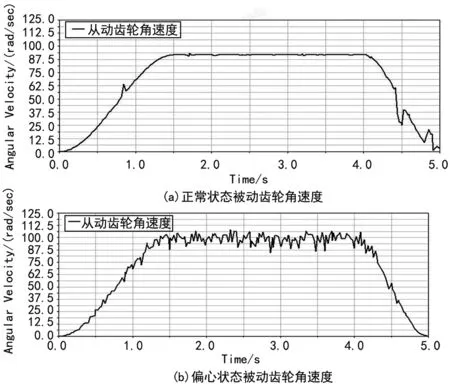
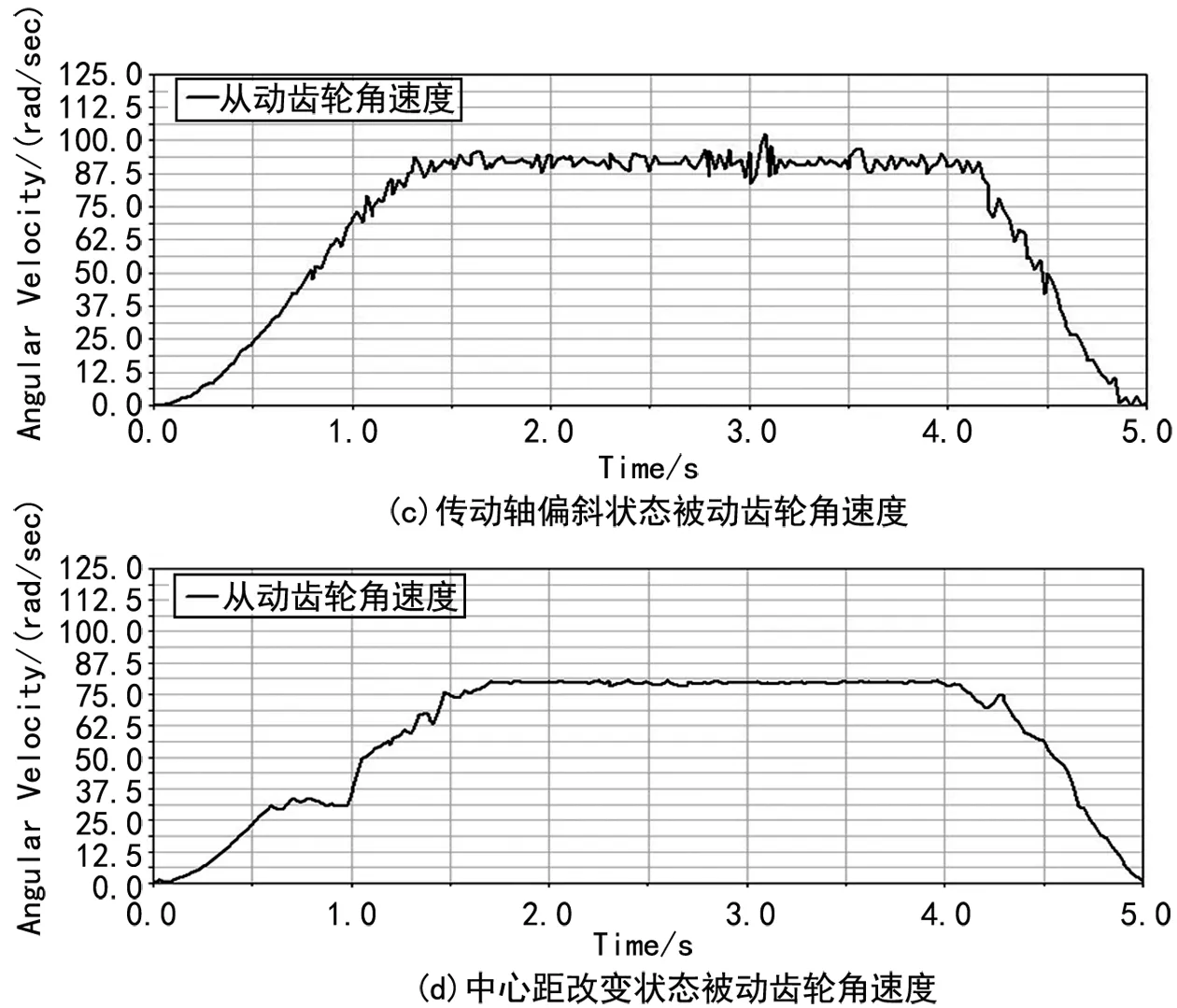
图3 各工况下从动齿轮角速度曲线

通过数据曲线，可以看出齿轮啮合时，角速度不是平稳的直线，而是在一定范围内波动的，通过ADAMS的数据处理功能，还可以得出角速度的极值和均值方便进行比较如表2。

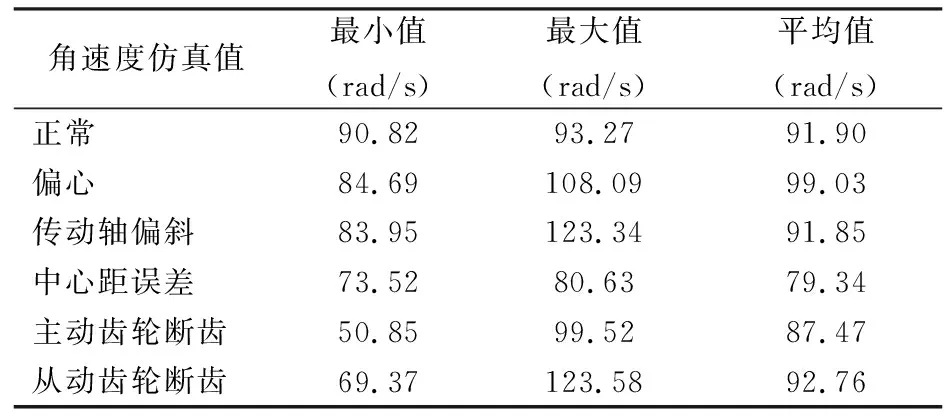
表2 各工况下1.5～4 s角速度仿真值

由图3及表2可以看出：

(2) 传动轴偏斜时，曲线波动主要以小坡度曲线为主，传动比均值与正常状态下相差0.05 rad/s，变化不大。说明传动轴平行度误差不大时，虽然平均传动正常，但是仍然存在瞬时传动比的变化。

(3) 中心距存在误差(偏大)时。从动齿轮角速度曲线较为平滑，波动情况不明显。但是角速度平均值仅为79.34 rad/s，明显小于理论值，说明此故障状态下，传动比较平稳，但是传动比明显减小。

(4) 当齿轮传动系统出现断齿故障时。角速度曲线呈锯齿状，齿轮啮合过程中产生瞬时传动比变化，而主动齿轮断齿比被动齿轮断齿角速度曲线波动更为剧烈，主要是由于主动齿轮转速要高于被动齿轮引起的，而两种故障状态下角速度平均值与正常状况差值小于5 rad，说明对平均传动比影响不是很大。

2.2 接触力曲线分析

通过ADAMS/PostProcessor模块，除了角速度曲线，还能得其它诸如加速度、力、力矩等许多测量值曲线，通过观察齿轮接触力曲线，与图3比较分析，检测角速度与接触力的关系。各工况齿轮啮合接触力曲线如图4所示。

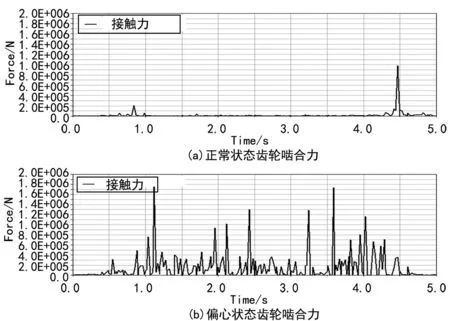
图4 各工况下齿轮啮合力曲线

通过数据曲线可以看出：

(1) 与被动齿轮角速度曲线相似，齿轮啮合力也不是平稳的直线，而是在一定范围内波动的，这样的数据更符合真实的齿轮啮合情况。当齿轮的第一对轮齿啮合后, 接触行为便一直存在。

(2) 啮合力的大小变化是因齿轮在克服负载转矩做功过程中两接触轮齿啮合时造成的接触变形量的变化引起的, 在齿轮加速或者减速阶段，随着速度的变化，负载增大，啮合力的大小一方面随着负载的增加而增大，另一方面呈周期性波动。

(3) 输入速度、外载荷和接触刚度系数都相同的情况下，主动齿轮转速稳定时，齿轮出现故障，啮合力曲线均呈锯齿状，其中以主动齿轮断齿时最为剧烈。

(4) 从动齿轮角速度的波动趋势与齿轮啮合力波动趋势基本保持一致，啮合力波动幅值大较大的故障状态的速度曲线波动幅值也大。角速度曲线越平稳，啮合力曲线也平稳。

3 结 语

将所建立的齿轮传动动力学模型导入MSC ADAMS，采用多体动力学方法对所建模型进行仿真分析，分析了齿轮传动系统在各种故障状态下的动力学行为表现形式，为机车牵引齿轮强度的提高和参数的优化设计提供了依据。