转动双星同步和轨道圆化的物理过程研究∗

李志 宋汉峰2)4)† 彭卫国 王靖洲 詹琼

1)(贵州大学物理学院,贵阳 550025)

2)(瑞士日内瓦大学天文系,瑞士,日内瓦 1290)

3)(凯里学院物理与电子工程系,凯里 556011)

4)(中国科学院天体结构与演化重点实验室,昆明 650011)

(2018年5月30日收到；2018年7月6日收到修改稿)

1 引 言

探索恒星结构与演化是天体物理的基础课题,它对了解星系乃至整个宇宙都有重要意义.宇宙中超过一半的大质量恒星为双星,双星的研究占有极其重要的地位.双星系统中由于两子星间的相互作用使得两子星的演化特征与单星有明显不同[1,2].近年来人们逐渐认识到转动效应是影响双星结构和演化非常重要的物理因素[3−7].Huang[8,9]提出:转动离心力使恒星内产生了新的物质运动形式——子午环流和剪切湍流.两种物理过程引起恒星内的化学元素扩散和角动量的转移,会对恒星结构与演化产生极其重要的影响.

在转动双星中两子星不但受到自转离心力的作用,并且受到潮汐力的作用.潮汐力拉伸每颗子星产生沿两子星连线方向的隆起[10−13].当子星的自转角速度与公转角速度不同时,潮汐隆起形成潮汐转矩.它使自转角速度与公转角速度趋向于一致,称为潮汐同步和锁定[14,15].潮汐同步过程不仅影响子星获得或失去自转角动量和子星内传输角动量的快慢,更重要的是在潮汐同步过程中,由于恒星表面和内部产生的强剪切效应,引起化学元素的强烈转移和混合,产生元素超丰现象.潮汐同步过程也会影响恒星内部自转角速度分布轮廓的变化,引起剪切湍流传输化学元素和子午环流传输角动量的效率.这些将极大地影响恒星的结构和演化[16−20].

然而精确计算大质量恒星的同步和轨道圆化过程是不容易的.恒星的初始转速、金属丰度、轨道周期、质量比率和对流超射等物理因素对其都有重要影响.本文详细研究了这些物理因素对潮汐同步和轨道演化的影响.在第2节中给出了计算潮汐同步和轨道圆化的基本公式,介绍角动量转移和元素扩散方程及边界条件和初始条件等；第3节中,用数值方法计算了这几种物理因素对恒星结构与演化的影响；第4节给出了主要结论.

2 潮汐同步和圆化时标、角动量转移和元素扩散方程

2.1 潮汐同步和圆化时标

潮汐可以分为两种.1)平衡潮汐.假设恒星结构对伴星引力场的扰动调整是处于流体静力学平衡的,平衡潮汐耗散最有效的形式是对流区域的湍流黏滞,它使潮汐效应产生的大尺度湍流的动能被分化成越来越小尺度湍流的动能,最终由于黏滞效应而消散成热能.如果耗散过程发生在恒星内部,平衡潮汐将落后于或超前于两星的连线,由此导致的力矩引起自转角动量和轨道角动量的转移.平衡潮汐通常应用在包层为对流区的恒星中,这时主星的同步时标可以表示为[15,21]

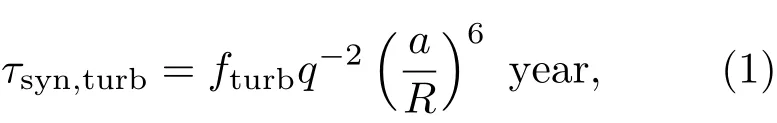
式中fturb=1,q=M2/M1为伴星和主星的质量比,M1为主星质量,M2为次星质量,a为双星间距,R为恒星半径.对应的圆化时标为[22]

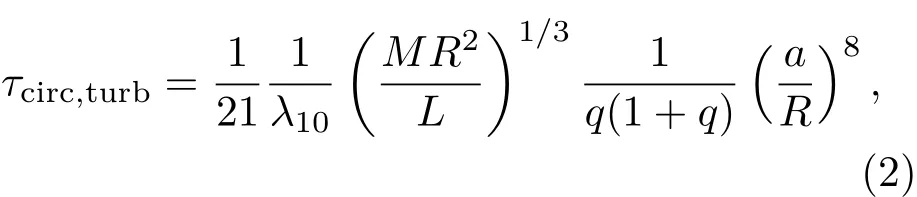
式中的λ10为转动恒星的结构参数,与拱线运动常数量级大小相似；L为恒星光度.

2)由于恒星震动所引起或驱动的动力学潮汐.拥有辐射包层的大质量恒星,在趋于同步转动的过程中,由于伴星引力场的变化,在恒星内产生一系列振荡.由于辐射衰减,这些振荡波在恒星表面被消散.选取双星系统的主星为研究对象,它的潮汐同步时标可表示为[14,15]

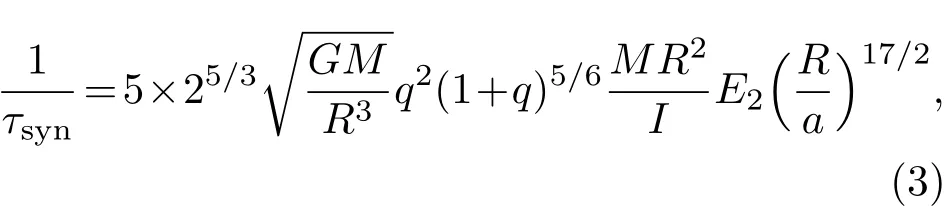
式中的E2=1.592×10−9(M/M⊙)2.84,I为转动惯量,对应的轨道圆化时标表示为

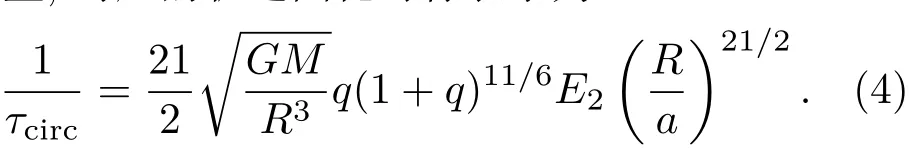
2.2 双星同步和轨道圆化方程

由于潮汐转矩,造成自转角速度的变化方程为

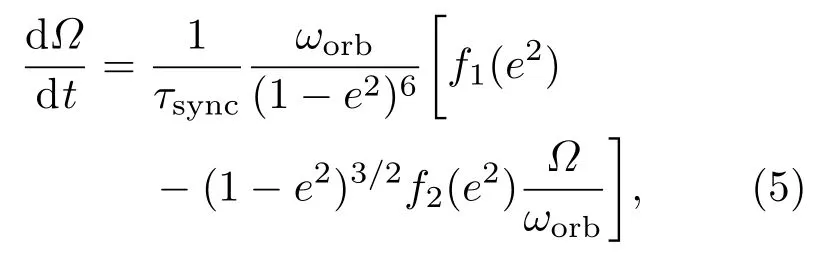
式中

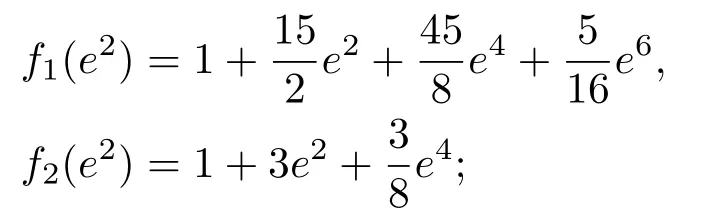
ωorb为轨道角速度,它可以写成ω=G(M1+M2)/a3；Ω为自转角速度；e为轨道偏心率.同理,由于潮汐摩擦造成的轨道圆化方程为

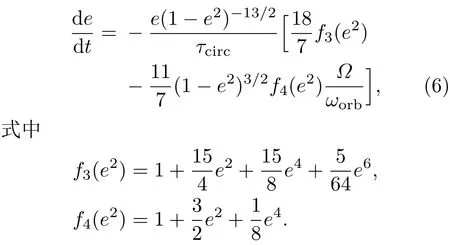
2.3 元素扩散方程和各种不稳定性造成的元素扩散系数

恒星中转动效应产生流体的各种不稳定性,造成恒星内部的元素混合和角动量转移.Endal和So fia[23]以及Pinsonneault等[5]假定长期不稳定性的元素混合率与角动量转移率成正比,可以得到由不稳定性导致的元素混合的径向扩散方程为

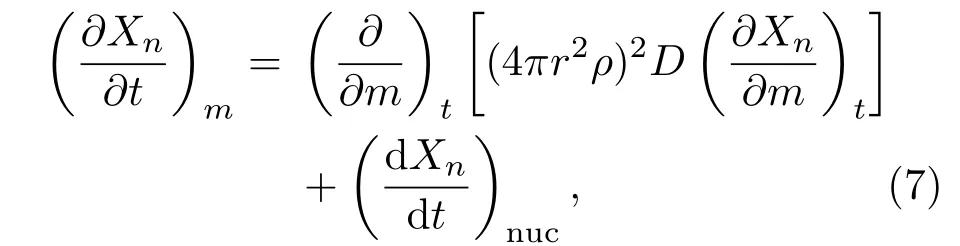
其中Xn是某种元素n的质量丰度；右边第一项表示扩散效应对化学元素丰度的影响,右边第二项表示核反应对化学元素丰度的影响.相应的边界条件为

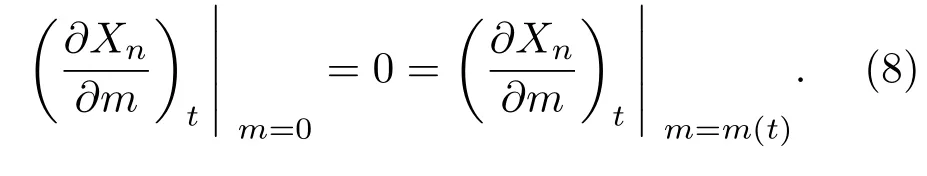
方程(7)中的D为元素扩散系数,包括对流和半对流及各种不稳定性对元素扩散的影响,可以表示为

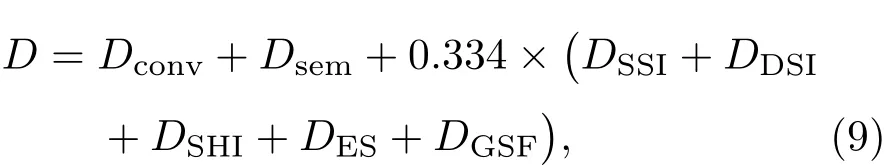
其中Dconv为对流不稳定造成的元素扩散系数；Dsem为半对流不稳定产生的元素扩散系数；DSSI为长期剪切不稳定产生的元素扩散系数；DDSI为动力学剪切不稳定产生的元素扩散系数；DSHI为Solberg-Hoiland不稳定产生的元素扩散系数；DES为子午环流产生的元素扩散系数,由于转动造成恒星产生变形,极区温度变高,赤道区温度变低,产生热不稳定,恒星内部形成大尺度子午环流[24],它是影响恒星内部角动量转移和元素扩散的主要因素；DGSF为Goldreich-Schubert-Frike不稳定产生的元素扩散系数.这些扩散系数的详细计算参见文献[25].

2.4 角动量转移方程

由于转动恒星中产生的这些不稳定,造成恒星内部的角动量转移.角动量转移方程可以写为[25]

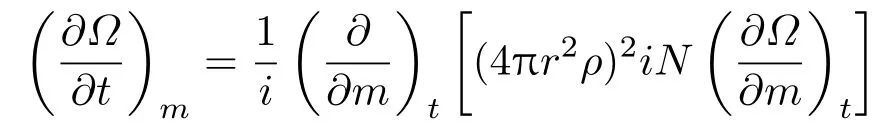
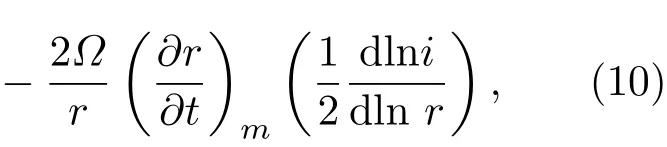
式中的i为质量坐标为m的单位壳层的转动惯量,设其内半径为ri,外半径为ro,则i=0.4(r−)/(+r).N为湍动黏度,可以写为

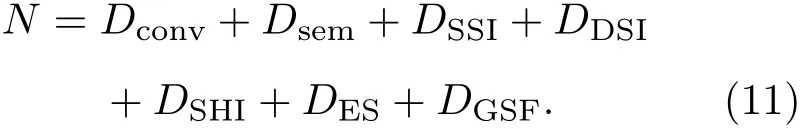
注意潮汐转矩作用在恒星的外表面,当作角动量转移方程的外边界条件.

3 数值计算方法及结果

我们采用Paxton等[26−28]编写的MESA程序做数值计算.初始模型选取为:零龄主序的恒星质量为15M⊙,金属丰度为Z=0.014,混合长参数取为2.0.采用Vink等[29]的星风公式做计算.各种模型的初始参数列在表1中.对单星模型计算到主序阶段结束,对双星模型计算到物质交换前停止.

图1给出了双星模型中同步时标随时间的演化.比较双星模型B1和B2,大质量恒星模型B2具有较小的潮汐同步时标.原因是:大质量星潮汐同步时标依赖于辐射衰减,近似为热时标.而大质量星的热时标短于小质量星.实际上,根据方程(3),当主星质量变大时,双星质量比q变小,潮汐同步应该变长.这说明潮汐同步时标对双星质量比并不敏感.对比模型B1和B3,低金属丰度恒星具有较长的同步时间,这是因为低金属丰度恒星的半径较小.同理,对比模型B1和B5,发现超射大的恒星具有较长的同步时标,也是因为恒星半径小的缘故.另外,初速度小的双星模型(如B6)比对应初速度大的双星模型(B1)的同步时标短.这与自转速度快的恒星将自转角动量转化为轨道角动量,轨道间距变长有关(见图4).随着恒星演化,所有模型的潮汐同步时标均变短,这些也是因为恒星半径随演化变大造成的.另外对比模型B1和B4,发现轨道周期长的系统,潮汐同步时间较长.这是因为轨道周期长的系统双星间距长,而潮汐同步时标对双星间距非常敏感,正比于双星间距的8.5次方.轨道周期大的系统,潮汐力矩迅速减弱.轨道圆化时标与同步时标变化有相似的结果.

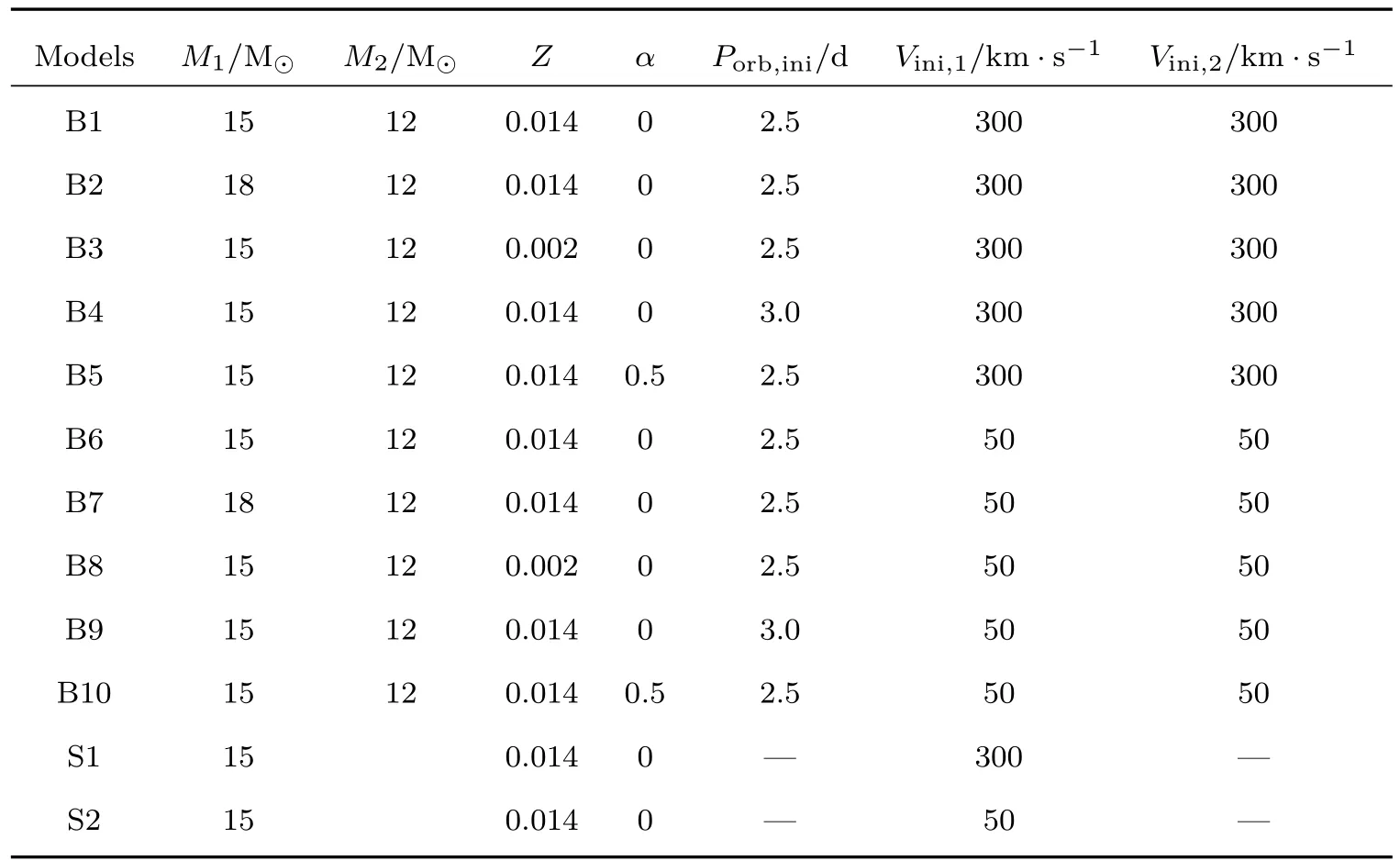
表1 单星和双星理论模型的初始参数Table 1.The initial parameters for single stars and binaries.

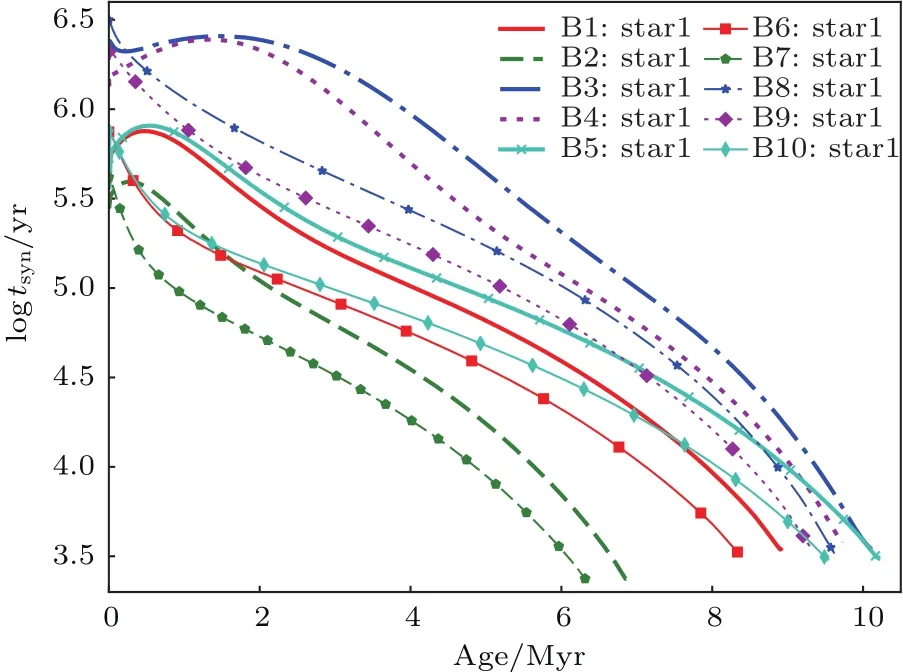
图1 双星模型中同步时标随时间的变化 双星模型(B1—B10)的初始偏心率为0.3,模型(B1—B5)的初始速度为300 km/s,模型(B6—B10)的初始速度为50 km/sFig.1.Synchronous timescales for the models of binaries vary with evolutionary time.The initial eccentricity are set to be 0.3 for the models of binaries(B1–B10),the initial velocities are set to be 300 km/s for models(B1–B5)and the initial velocities are set to be 50 km/s for the models(B6–B10).

图2(a)和图2(b)给出了单星和双星模型中的主星的赤道速度随时间的演化.从图2(a)可以看出,单星模型的赤道转动速度大于对应双星模型中的主星的转动速度.原因是:潮汐转矩对初速度大于轨道速度的恒星产生减速,使恒星自转速度与轨道速度趋于一致.达到同步后,我们发现B1和B4模型中的自转速度Veq,1略小于对应的轨道速度Vorb,1.原因是:潮汐转矩正比于自转角速度和轨道角速度之差,在同步转动状态Veq,1=Vorb,1,潮汐转矩为零.星风转矩进一步减速恒星,使自转角速度进一步减小.当潮汐转矩和星风转矩平衡时,恒星达到平衡速度.而平衡速度比轨道速度略小,它与轨道速度的差值及星风强弱有关.自转角速度锁定在平衡速度,随着恒星半径逐渐增加,自转速度逐渐增加.

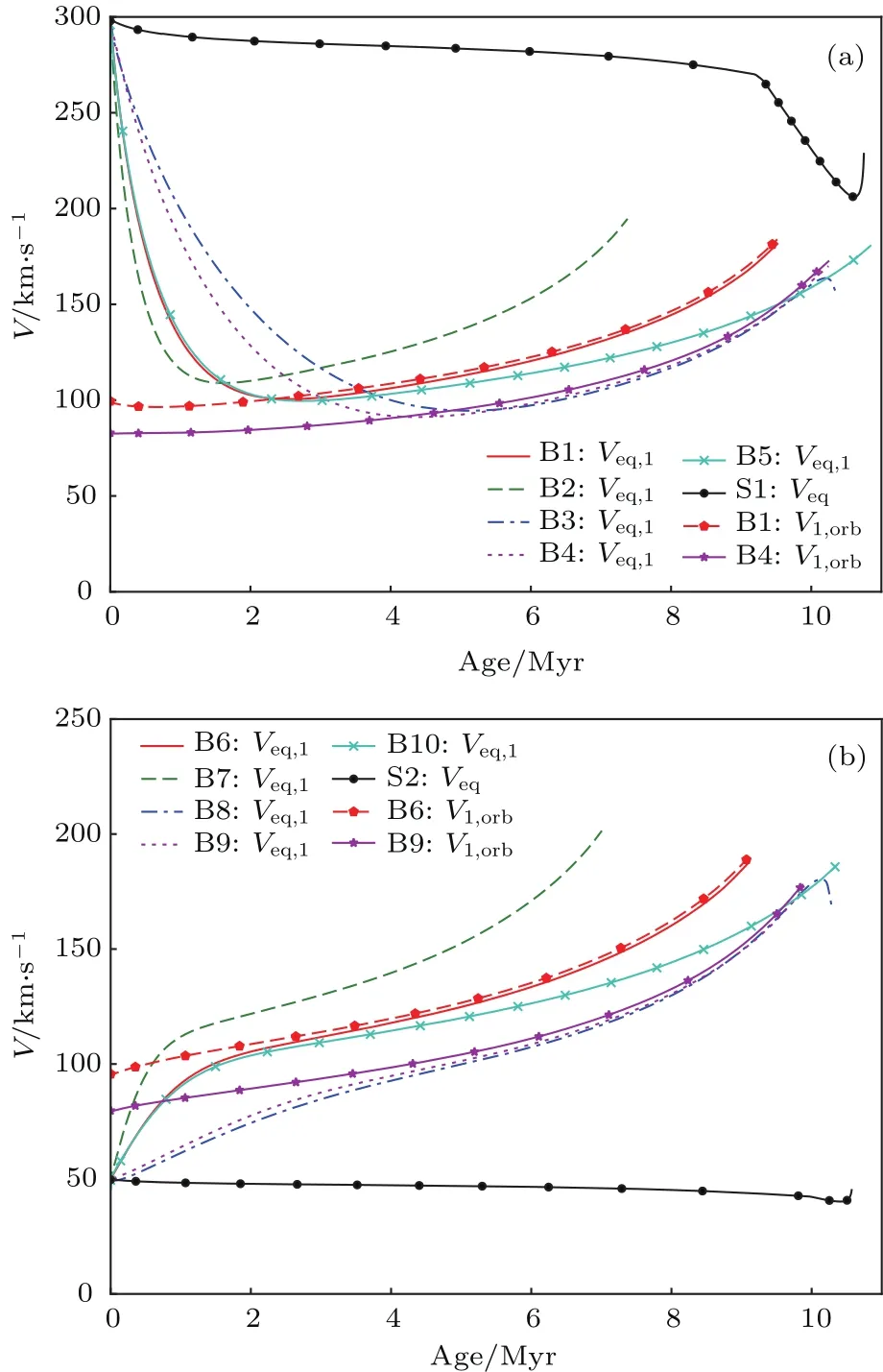
图2 (a)初始速度为300 km/s时,双星模型(B1—B5)中主星和单星模型S1的赤道速度随时间的变化,作为对比,给出了双星模型中B1和B4的轨道速度；(b)初始速度为50 km/s时,双星模型中主星(B6—B10)和单星模型S2的赤道速度随时间的变化,作为对比,给出了双星模型中B6和B9的轨道速度；双星模型(B1—B10)的初始偏心率为0Fig.2. (a)Equatorial velocities vary with evolutionary timefor the models of single stars S1 and binaries(B1–B5),the initial velocities are set to be 300 km/s；(b)equatorial velocities vary with evolutionary timefor the models for single stars S2 and binaries(B6–B10),the initial velocities are set to be 50 km/s.The initial eccentricity are set to be 0 for the models of binaries(B1–B10).

对比B1和B2,发现B2模型中的主星在潮汐同步减速过程中速度减小速度较快,达到平衡速度时具有较高的速度.原因是大质量恒星的同步时标短,它又具有较大的半径.对比B1和B3,发现低金属丰度恒星B3模型潮汐减速过程较慢,达到的平衡速度小.原因是:潮汐同步时标约反比于恒星半径的7次方.低金属丰度的恒星具有较小的半径,因而同步减速时间较长.对比B1和B4,发现长周期的双星系统,潮汐减速过程较慢,达到的平衡速度小.这是由于潮汐同步时标正比于双星间距的8.5次方,长周期双星系统的潮汐转矩较小、而轨道角速度也较小造成的.对比B1和B5,结果显示对流超射大的恒星,其平衡速度较小.

从图2(b)可以看出,双星模型(B6—B10)的转动速度均大于单星S2的转动速度.原因是潮汐转矩对自转角速度小于轨道角速度的子星产生潮汐加速作用.潮汐效应是产生快速转动恒星的方式之一.对比模型B6和模型(B7—B10),发现大质量、短轨道周期、高金属丰度和对流超射小的子星潮汐转矩大,因而潮汐加速过程比较快.对比双星系统B6和B9的赤道速度和轨道速度,显示双星模型中子星的赤道速度均小于对应的轨道速度.这说明对于初始速度小于轨道速度的情况,同步转动状态是不可能达到的.原因是当恒星的自转速度接近轨道速度时,潮汐转矩变得越来越弱,并趋于零.星风转矩阻止其达到同步状态(Veq,1=Vorb,1),但子星可以达到平衡速度(即潮汐转矩和星风转矩相平衡的状态).

图3(a)给出了双星系统轨道偏心率随时间的演化.结果表明:初始转动速度快的双星系统(B1—B5),系统轨道偏心率随时间先增长后减小；初始转动速度慢的双星系统(B6—B10),系统轨道偏心率随时间永远减小(参见图3(c),(de/dt)tide＜0). 原因是:根据方程(6),当Ω/ωorb＞18/11时,de/dt＞0,因而初始角速度快的系统,潮汐摩擦反而增加轨道偏心率(参见图3(b),(de/dt)tide＞0).正是由于这个原因,对初始速度快的恒星(B1—B5),轨道圆化的时间被延长.但当Ω/ωorb＜18/11时,de/dt＜0.表明在初始速度较高的双星系统,潮汐同步过程减小恒星的转动速度,促进轨道偏心率减少.

对比B1模型中的子星,从图3(b)和图3(c)可以看出:具有低金属丰度、轨道周期长、低质量且超射较大的系统,轨道圆化速度较慢,系统具有较大的轨道偏心率.对初始轨道周期大的双星系统B4可以达到较大的轨道偏心率e∼0.42.

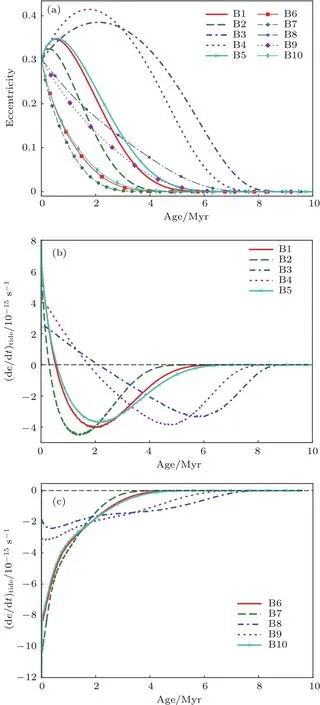
图3 (a)双星系统轨道偏心率随时间的演化；(b)初始速度为300 km/s的双星系统(B1—B5),潮汐摩擦造成的轨道偏心率随时间的演化；(c)初始速度为50 km/s的双星系统(B6—B10),潮汐摩擦造成的轨道偏心率随时间的演化；双星模型(B1—B10)的初始偏心率为0.3Fig.3.(a)Orbital eccentricity vary with evolutionary timefor the models of binaries；(b)the variation rate of orbital eccentricity induced by tidal friction in the binaries with the initial velocities of 300 km/s；(c)the variation rate of orbital eccentricity induced by tidal friction in the binaries with the initial velocities of 50 km/s.The initial eccentricity are set to be 0.3 for the models of binaries(B1–B10).

图4给出了双星系统轨道周期随时间的演化.结果显示,对于初始转速快Veq=300 km/s的双星模型,轨道周期先增加后减少.原因是:当恒星自转角速度大于轨道角速度时,潮汐转矩将子星的自转角动量转化为轨道角动量,恒星自转速度变慢,双星间距增加,双星系统轨道周期增加.对于初始轨道周期为3.0 d的双星系统B4,轨道周期变大的幅度最大,意味着有更多的自转角动量转化成为轨道角动量.但当恒星自转角速度小于轨道角速度时,潮汐转矩将系统的轨道角动量化转为子星的自转角动量,双星间距减少,双星系统轨道周期逐渐减小.

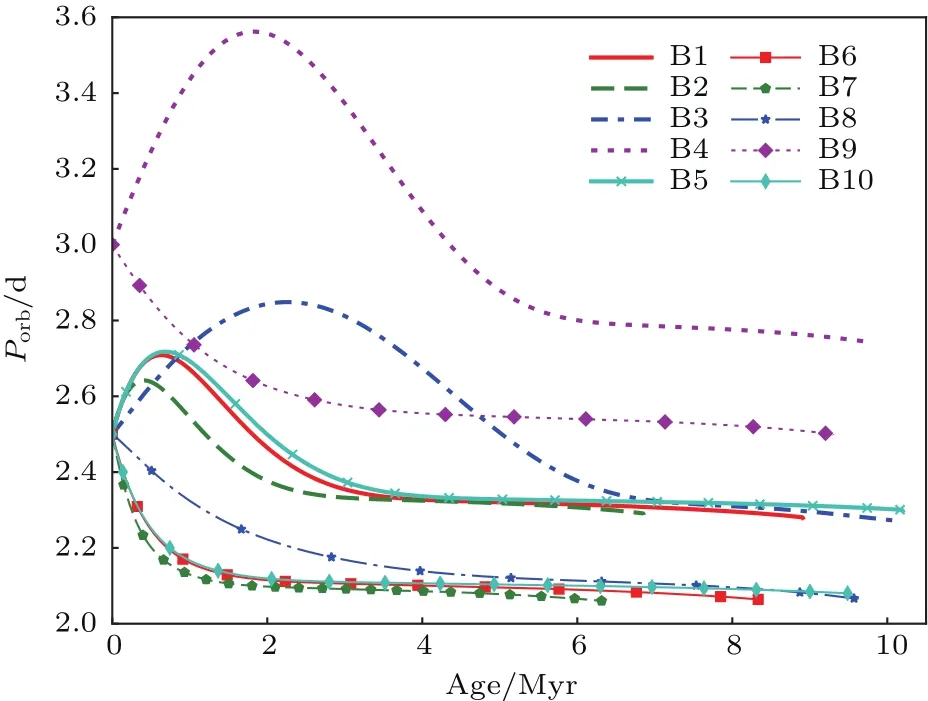
图4 双星系统轨道周期随时间的演化,双星模型(B1—B10)的初始偏心率为0.3Fig.4.Orbital periods vary with evolutionary timefor the models of binaries.The initial eccentricity are set to be 0.3 for the models of binaries(B1–B10).

对于初始转速慢,Veq=50 km/s的双星模型,轨道周期始终减少.意味着潮汐转矩始终将系统的轨道角动量化转为两颗子星的自转角动量,双星间距减少,双星系统轨道周期逐渐减小.当双星系统的子星达到平衡速度后,轨道周期略微变小,近似保持为常数.因为这时潮汐转矩与星风减速转矩相平衡,而星风转矩对轨道演化的影响很小,可以忽略,所以轨道周期近似为常数.实际上,自转角动量与轨道角动量间的转化效率就是潮汐转矩的大小,因而潮汐转矩影响轨道周期的变化率.

图5给出了单星模型S1和双星模型(B1—B5)中恒星表面氮丰度随时间的演化.结果显示,随着恒星演化,单星模型S1中恒星表面的氮增丰比双星模型中主星的氮元素增丰显著.原因是:在我们的模型中,子午环流是元素混合的最主要物理因素,环流速度与转动角速度的平方成正比.单星的转动速度快,而双星的转动速度由于受到潮汐同步的影响,转速减慢,因而元素混合变慢.另外可以看到,低金属丰度的恒星,表面氮丰度较低.原因是:低金属丰度的恒星初始的C,N,O丰度较低,因而由C元素和O元素转化成N元素的丰度较低.由图中可以看出,大质量星表面氮增丰快,这是因为子午环流随辐射压的增大而增大,元素混合时标与主序演化时标的比率与恒星的质量的1.1次方成反比[30],对同一个初始转动速度,大质量星的元素混合较快.此外,对比双星模型B1和双星模型B4和B5,结果显示超射大(B5)和周期短(B1)的双星系统氮元素增丰较显著.超射大的恒星,说明在核反应区由C,O元素转化为N元素比较多,较容易扩散到恒星表面.短周期系统则是平衡速度比较大、环流速度大、增丰显著造成的.

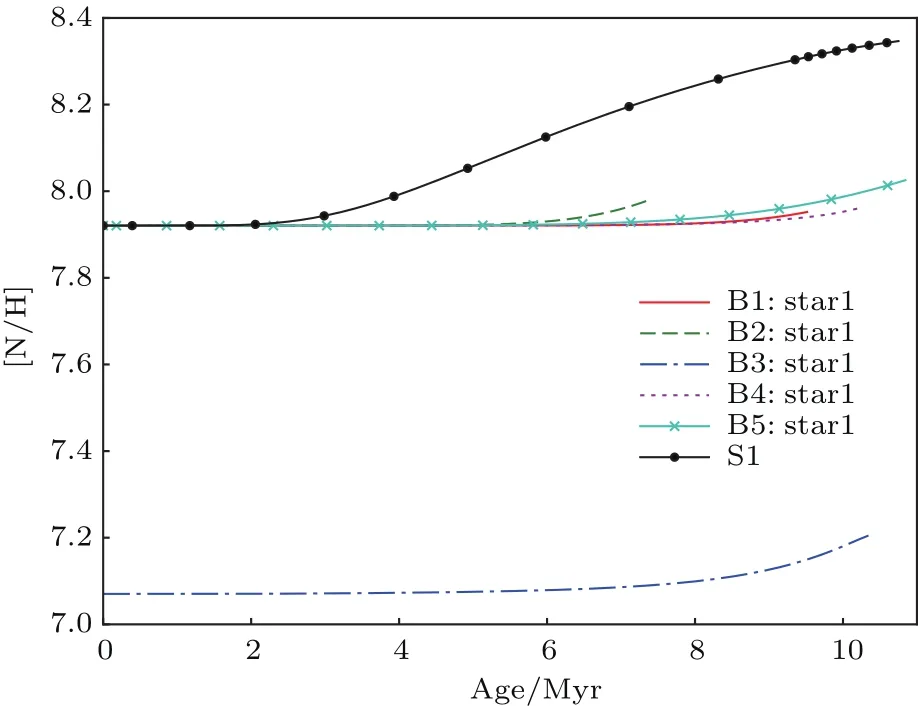
图5 单星和双星模型中恒星表面氮丰度随时间的演化,初始速度为300 km/s,双星模型的初始偏心率为0Fig.5.Surface nitrogen abundances vary with evolutionary timefor the models of single stars and binaries with the initial velocities of 300 km/s.The initial eccentricity are set to be 0 for the models of binaries.

图6(a)给出了单星模型S1和双星模型(B1—B5)中恒星半径随时间的变化.从图中可以看出,双星模型B2中的主星具有最大的恒星半径,因为其具有较大的质量.双星模型B3中的主星,因为具有较小的金属丰度,而具有最小的恒星半径.对比单星模型S1和双星模型B1,可以看出,单星模型S1具有较大的恒星半径.原因是单星模型具有较快的转速,强离心力减小了恒星包层的重力,恒星更容易膨胀的缘故.对比双星模型B1,超射大的恒星B5,具有较小的恒星半径.对比模型B1和模型B4,发现轨道周期对恒星半径演化的影响很小.

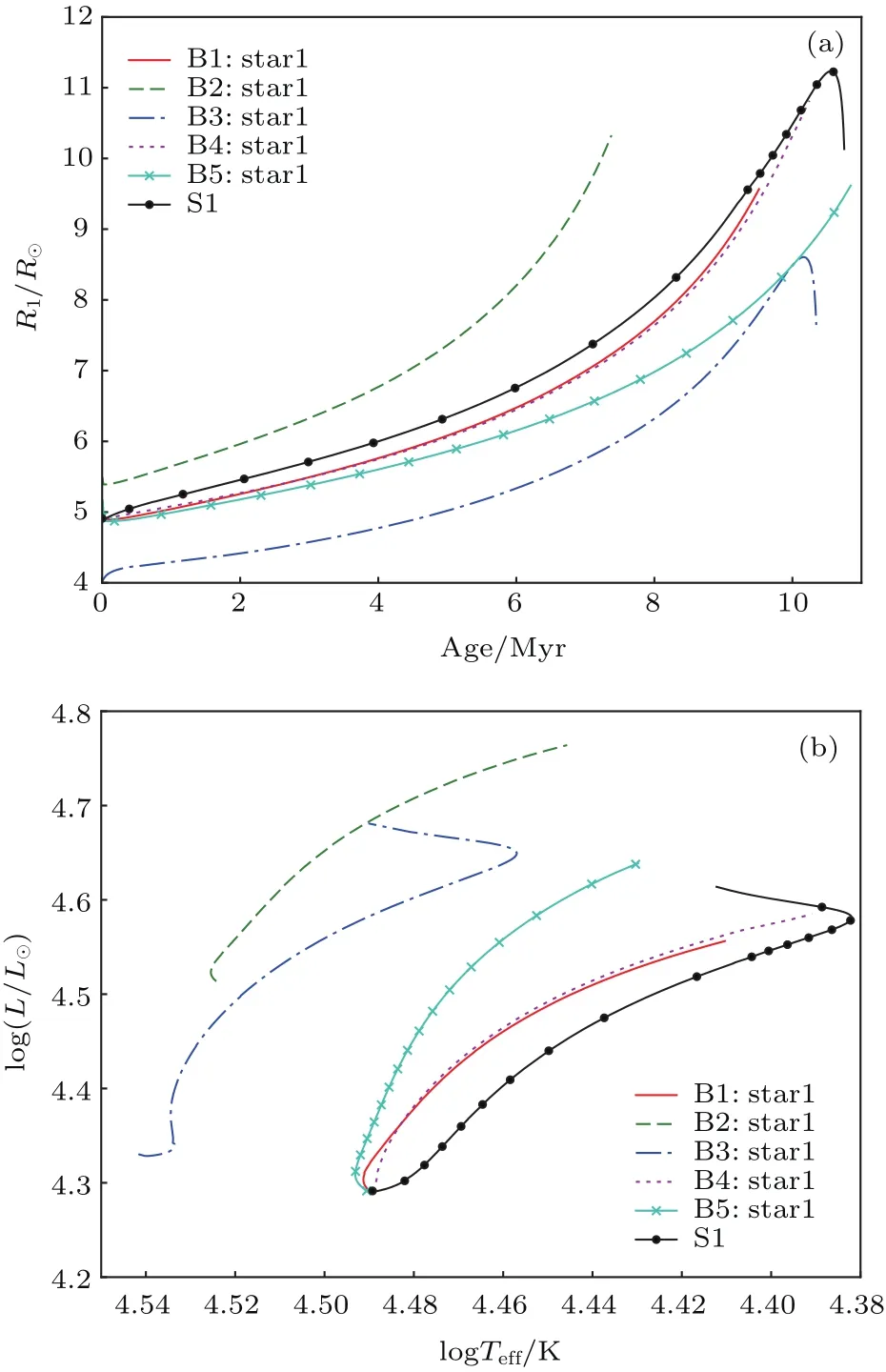
图6 (a)单星和双星模型中恒星半径随时间的变化,初始速度为300 km/s；(b)单星和双星模型中恒星在赫罗图中的演化,初始速度为300 km/s；双星模型的初始偏心率为0Fig.6. (a)Stellar radii vary with evolutionary timefor the models of single stars and binaries with the initial velocities of 300 km/s；(b)the evolution of the primary stars in HR diagram for the models of single stars and binaries.The initial eccentricity are set to be 0 for the models of binaries.

图6(b)给出了单星和双星模型中恒星在赫罗图中的演化.从图中可以看出,双星模型B2中的主星由于具有较高的中心温度和质量,因而具有最大的恒星光度.双星模型B3中的主星由于具有较小的金属丰度,表面具有较高的有效温度.对比单星模型S1和双星模型B1可以看出,单星模型S1的恒星表面具有较低的有效温度和光度.原因是单星模型具有较快的转速,强离心力减小了恒星的有效质量,因而具有低的有效温度和光度.另外,按照引力昏暗效应,恒星光度正比于表面重力加速度[31],强离心力也减小了恒星表面的有效重力加速度,因而光度较低.对比双星模型B1,超射大的恒星B5具有较大的恒星光度.原因是对流超射增加了中心对流区,有更多的氢元素参加核反应,使总产能率增加.对比模型B1和模型B4,发现双星的轨道周期对恒星的演化影响不大.

4 讨论与结论

1)潮汐同步与轨道圆化是影响转动双星结构与演化非常重要的物理因素.潮汐同步和与圆化时标与恒星质量、初始转速、轨道周期、金属丰度,对流超射等物理因素有密切关系.结果表明,质量大的恒星,初始转速慢、对流超射小.轨道周期短的双星系统,潮汐同步时标和轨道圆化时标短,双星系统更容易达到同步和轨道圆化.随着恒星演化,潮汐同步和轨道圆化时标均变短,这是恒星半径变大的原因造成的.

2)由于潮汐同步,使初始速度大的恒星赤道转动速度小于对应的单星模型,使初始速度小的恒星赤道转动速度大于对应的单星模型.潮汐效应是恒星具有较高速度的原因之一.对初速度高于轨道速度的子星,由于潮汐转矩在同步转动状态时为零,星风转矩进一步减速恒星,子星不能永久保持在同步状态,但恒星速度可以长期保持在平衡速度(即:潮汐转矩与星风转矩相平衡的速度).对初速度低于轨道速度的子星,子星不可能达到同步状态,但可以达到平衡速度.平衡速度低于同步转动速度,两者差值大小与星风强弱有关.

3)初始速度的大小影响轨道圆化.当Ω/ωorb＞18/11时,de/dt＞0.具有快速转动、低金属丰度、轨道周期长、质量低且超射较大子星的系统,轨道圆化速度慢,因而系统可以具有较大的轨道偏心率.初始转动速度快的子星,自转角动量通过潮汐转矩转变为轨道角动量,轨道间距变长,使潮汐同步和轨道圆化速度变慢.初始速度慢的子星,潮汐转矩始终将轨道角动量转化为自转角动量,轨道间距变短,潮汐同步和轨道圆化速度快.因而初始转动速度决定潮汐同步和轨道圆化的速率.

4)初始转动速度大的子星,由于潮汐同步过程,转动速度变慢,因而双星系统中氮元素增丰没有单星的氮元素超丰显著.大质量、高金属丰度、超射大和短周期的双星系统,氮增丰相对显著.质量小、低金属丰度、转动速速慢、超射大的恒星具有较小的恒星半径.低金属丰度恒星表面具有高的有效温度,而超射大的恒星具有较高的光度.轨道周期对恒星结构和演化(恒星半径、中心温度、中心集中度、光度等)的影响很小,可忽略.快速转动使单星向低温和低光度端演化.