关于角动量的教学探讨*
周鹏宇 李晗 宋更新 刘 帅 王 波 侯朴赓
(东北电力大学理学院 吉林 吉林 132012)(吉林农业科技学院文理学院 吉林 吉林 132101)(东北电力大学理学院 吉林 吉林 132012)
角动量是研究物体转动的重要物理量, 是转动动力学的核心概念之一.目前, 绝大多数大学物理教材在介绍角动量时[1~7], 都是先定义质点角动量, 再通过质点角动量推演出刚体和一般质点系的角动量.然而, 由于质点角动量是力学中最初涉及物理量间矢积运算的物理量之一, 它与学生之前所遇到的物理量都不相似, 具有明显的特殊性, 会使初次接触它的学生感到十分陌生, 不容易理解和掌握.本文提出了讲解和阐释刚体、质点以及一般质点系角动量概念和相关理论的新思路: 通过将描述刚体转动物理量和描述质点平动物理量进行类比, 引入刚体角动量概念及其表达式; 利用转动定律推导出角动量定理, 阐释角动量引入的合理性和物理意义;再通过刚体角动量的表达式讨论得出质点角动量和一般质点系的角动量, 说明角动量概念及其相关理论的普适性.
用来研究刚体定轴转动的物理量, 如角速度ω,转动动能ET,转动惯量J,力矩M和角加速度α等, 与用来研究质点运动的物理量, 如速度v,动能Ek,质量m,力F和加速度a等具有很强的对应关系, 比如:ω和v相似, 都代表研究对象运动的快慢; 刚体的ET可由质点的Ek导出, 且表达式相似
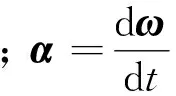
L=Jω
(1)
那么猜想得到的这个新概念是否合理和有意义呢?这需要验证一下.如何验证?可以检验它与已知物理量间是否存在联系, 或者看看它是否可以由已知的物理量衍生出来.由于角动量L表达式中含有J和ω两个量, 因此它应与力矩M有紧密联系; 因为M=Jα, 与L相似都是由转动惯量和角量构成.将M=Jα式子的两边同时对时间积分得
(2)
由此可知, 作用在刚体上的力矩对时间的累积等于刚体末态角动量和初态角动量之差, 这表明是一个用来描述刚体转动的状态参量.
一般情况下, 刚体可能会同时受到多个力矩作用.按照这些力矩来源的不同可将它们划分为内力矩和外力矩.对于刚体(或一般物体)而言, 内力是源于其内部各质元的相互作用, 由牛顿第三定律可知, 作用力和反作用力始终大小相等、方向相反, 且作用的位置相互重合; 由此可知作用力和反作用力形成的力矩必然是大小相等方向相反的, 又由于作用力和反作用力总是成对出现, 因此可知它们对总力矩贡献为零, 即内力矩之和为零.由此推论, 一个刚体(或一般物体)角动量的变化应来源于合外力矩的作用, 即
(3)
此为角动量定理.
角动量定理还有一个重要的推论: 当合外力矩M外=0时,L2=L1.该推论称为角动量守恒定律.
上面通过类比法, 引入刚体角动量概念, 并且讨论得出角动量和力矩之间的关系, 以及角动量守恒.对于角动量这个概念, 它不仅可以用来描述刚体转动, 而且可以用来描述和研究一般的质点和质点系的运动, 例如:绕固定点作匀速圆周运动的质点, 假设质点质量为m, 圆周半径为R, 角速度为ω, 那么, 该质点相对于固定点的转动惯量为
J=mR2
其角动量为
L=Jω=mR2ω
下面来考虑作一般运动质点相对于空间中某参考点的角动量.
如图1所示, 一质点, 其质量为m, 速度为v, 相对于参考点O的位矢为r.质点运动过程中位矢r相对于水平线的夹角θ随时间变化, 因此质点相对于点O应具角速度ω.将v向与r平行和垂直的两个方向上投影, 分解成v∥和v⊥.
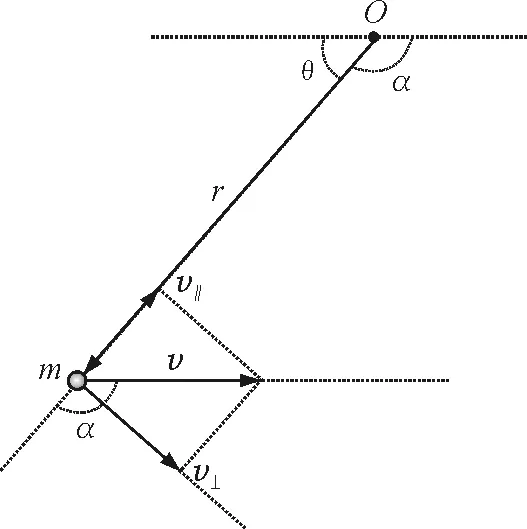
图1 求解质点m相对于参考点O的角动量的示意图
由图像可知, 只有v⊥对ω有贡献, 而v∥对ω无贡献; 利用角速度和线速度的关系可得
那么, 该质点相对于O点的角动量为
根据图1中各矢量的关系可得, 质点角动量表达式的矢量形式应为
L=r×mv=r×p
(4)
单一质点相对于某一参考点的角动量也可视为该质点相对于穿过该参考点且与速度矢量和参考点所在平面垂直的假想轴的角动量[8], 那么可推知, 由多个质点构成的质点系相对于某个轴也应具有角动量.根据矢量的可叠加性可知, 某一质点系的总角动量应等于其内部各个质点的角动量之和, 即

(5)
以上讨论表明, 质点和质点系的角动量表达式可由刚体角动量表达式衍生出来, 因此质点和质点系相对于某个参考点的角动量同样满足角动量定理和角动量守恒定律.

