国债远期利率的量子场理论模型构建∗

雷丽梅 冯玲

(福州大学经济与管理学院,福州 350002)

(2018年3月12日收到；2018年8月7日收到修改稿)

1 引 言

在现实世界中,由于复杂的交互作用和多样化机理使得时间序列可能包含隐含的相关性信息,这些相关性的特性对理解它们的本质和机理至关重要.而在成熟的金融市场中,几乎所有利率衍生产品的定价都取决于远期利率,探寻一种更符合实际的远期利率曲线的统计模型对风险控制和利率衍生品的定价和对冲至关重要.虽然目前我国的利率衍生产品种类不多,但随着我国利率市场化改革的全面推进和对外开放的进一步扩大,引进这些金融工具势在必行.因而,研究我国国债远期利率的精确与合理建模,为不久的将来中国利率衍生产品的开发、设计及应用提供定价依据与支持,具有重大的理论意义和实际意义.

在利率的建模方面,众多学者提出了大量的利率模型,包括单因子均衡模型,如Merton模型、Vasicek模型和CIR模型；多因子均衡模型,如Brennan-Schwartz模型、Fong-Vasicek模型和Longstaf f-Schwartz模型；带机制转换的均衡模型,如RSCIR模型；无套利模型,其典型代表是Heath-Jarrow-Morton(HJM)模型和LMM模型,而它们也是当前利率及其衍生品建模的主流模型,已经成为大量有关利率衍生品定价和对冲研究的基础.但是经典的HJM模型和LMM模型的主要局限性在于:将远期利率作为一维的随机过程来模拟,即假定不同到期期限的所有远期利率均是完全相关的,而在实际的金融市场中,不同到期期限的远期利率并非完全相关.虽然之后有很多学者[1−5]从引入波动率结构和相关性的角度对HJM模型和LMM模型进行了各种修正和拓展,虽然可以考虑这种不完全相关性,但即使引入有限个白噪声也无法捕捉到相关性函数的所有信息,例如一个K因子HJM模型,意味着K个债券价格的变化将决定所有其他债券的价格运动,即在K因子HJM模型框架下,用K个债券即可对冲任何固定收益工具,这显然是不符合实际的.如一个两因子HJM模型意味着可以用一个3个月期限和一个6个月期限的票据来对冲一个10年期的国债,这显然是不合理的.而引入无限个白噪声,在实践中这些方法均变得无效.因而,迫切需要寻求一种更符合实际的新的远期利率模型.

近几年,来自物理(特别是统计物理和量子场理论)的概念已经显示出其在金融理论和应用上的巨大潜力[6−16]. 特别地,Baaquie等[17−23]开始将量子场理论引入到衍生品定价方面的研究,并处理金融中的随机过程.本文利用量子场理论对我国国债瞬时远期利率进行建模,与随机微积分相比,来自量子场理论的一些方法在描述远期利率的波动和相关性时具有更大的优势.与传统的远期利率建模不同(传统的远期利率建模只考虑了在日历时间方向上的相关性),本文的一个主要创新在于利用量子场理论有效纳入了国债瞬时远期利率在日历时间和到期时间两个维度上的相关性,以提高远期利率模型对市场数据的拟合精度；本文的第二个创新之处在于,运用量子场理论技术直接对国债远期利率的实际市场演化建模,模型所需估计的参数均直接由市场数据拟合得到,而不像传统金融上的动态利率期限结构,需要事先对波动率函数或其他参数的函数形式进行设定,且随着引入因子个数的增加,模型估计会越来越困难.

本文主要从研究国债远期利率的瞬时变化的相关性结构入手,运用量子场理论技术,试图在保持模型简单的同时,建立一个更加符合实际的新的国债远期利率模型.本文第2部分对文中所用到的模型进行简要的基础理论介绍；第3部分构建最优的量子场理论模型,并将所构建的场理论模型结果与金融业内应用最广泛的两因子HJM模型的实证结果进行比较；第4部分是将第3部分估计所得的最优参数分别代入各最优模型进行回测检验,用于验证考虑日历时间和到期时间两个维度上的国债远期利率之间不完全相关性的量子场理论模型对市场数据的拟合效果的优越性；第5部分为结论.

2 模型描述

2.1 传统金融上的HJM模型

在金融应用上,利率衍生品的定价要求由利率模型所推导出的债券价格必须与实际初始期限结构一致,进而对基础证券进行套期保值.出于这一目的,Heath,Jarrow和Morton[24]于1992年提出了HJM分析框架,给出了无套利模型的一般形式.HJM分析框架从设定瞬时远期利率在现实测度下的随机过程出发,将当前的利率期限结构作为输入变量,基于无套利条件推导出风险中性测度下瞬时远期利率所应遵循的随机过程,进而求解债券与衍生品价格.

记f(t,T)表示远期利率,则在K因子HJM模型中,远期利率的演化为

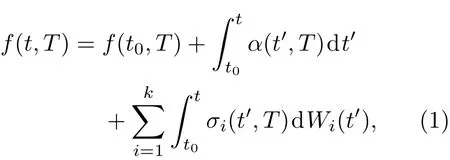
式中,f(t0,T)是t0时刻观测到的瞬时远期利率,即初始远期利率曲线；α(t,T)和σi(t,T)分别对应现实世界的瞬时远期利率的漂移率和波动率；Wi(t)(i=1,2,...k)是k个相互独立的标准维纳过程.也可写成

其中ηi(t)表示相互独立的高斯白噪声.

可推出HJM框架下瞬时远期利率的风险中性随机过程为

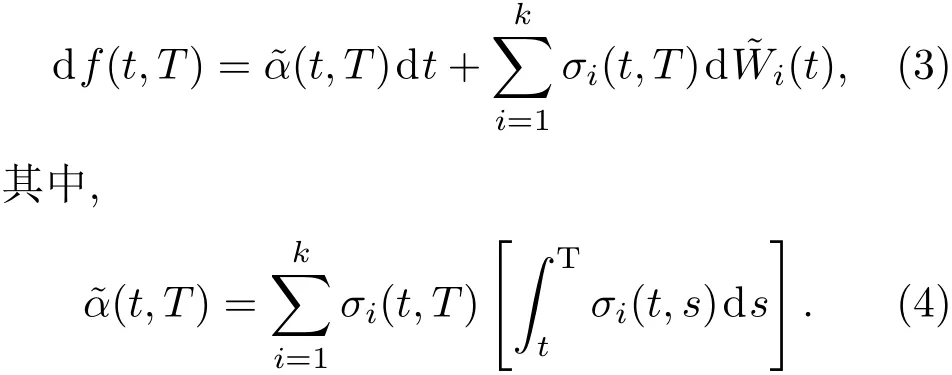
(4)式是HJM分析框架的核心结论.它意味着在无套利条件下,风险中性测度下瞬时远期利率的漂移项是波动率的函数,波动率完全决定了瞬时远期利率的风险中性过程,而在HJM分析框架下,风险中性测度和现实测度下的波动率是相同的.因而,在HJM框架下,只要给定波动率,同时运用初始远期利率曲线,就可以为利率产品定价.

2.2 远期利率的量子场理论模型

在K因子HJM模型中,远期利率的演化是由K个独立的高斯白噪声驱使的,它们对所有远期利率的冲击是一样的,即HJM模型假定所有远期利率的波动是一样的,这在现实中是不合理的.而将每个不同期限的远期利率作为独立的随机变量已经通过随机偏微分方程得到研究.用广义的连续随机过程来纳入远期利率间不完美的相关性的研究包括Kennedy[25,26],Goldstein[27],Santa-Clara和Sornette[28].Baaquie[17]以及Kim等[29]按照这个思路,将所有这些模型纳入量子场理论的框架内进行了推广.

Baaquie[19]基于将(1)式中的白噪声用一个量子场取代,将远期利率的演化方程以速度量子场A(t,T)形式写为

其中,远期利率f(t,T)和它衍生的速度场A(t,T)均被认为是一个二维量子场.

场理论模型对HJM的主要扩展在于A(t,T)既依赖于t,也依赖于T,而不像HJM中的白噪声W(t)只依赖于t.而尽管可以放入多个场Ai,但分析表明使用一个场就足以描述利率的行为.因而,量子场论下的远期利率模型为

此外,与HJM模型通常假定波动率函数σ(t,T)的形式不同,场论方法中的波动率可直接由市场数据拟合得到,不需要对其函数形式进行事先假定,而漂移项α(t,T)则由鞅条件确定.

可自由选择量子场A(t,T)的动态性.根据Baaquie[20]的分析,描述瞬时远期利率演化的Lagrangian是由参数µ和λ来定义:

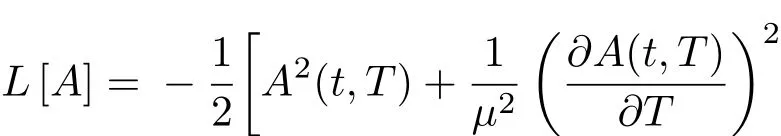
进而,可得出相应的action指数S[A]:

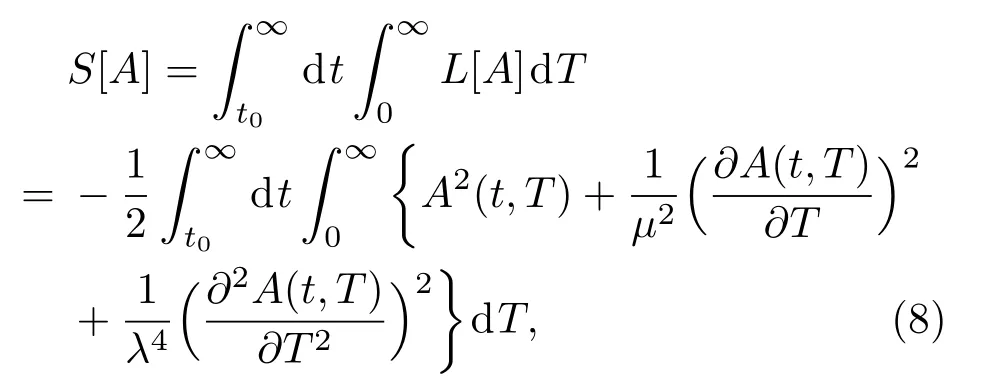
其中,µ是描述场A(t,T)一个“rigidity”参数,λ描述的是远期利率曲线的“stiffness”,上面定义的量子场理论称为刚性作用量下的量子场理论.

远期利率的量子场理论是通过对A(t,T)的所有变量的一个泛函积分来定义,并得到配分函数:

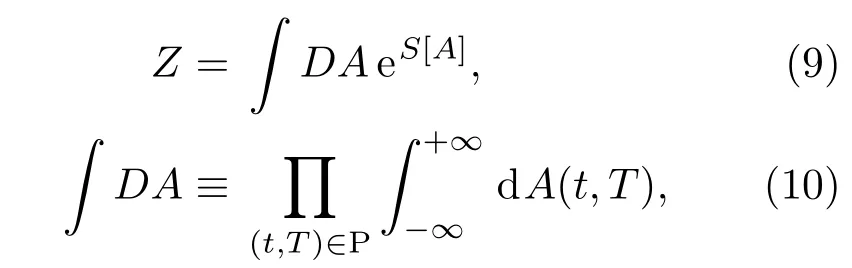
其中,P表示远期利率的定义域,如图1所示.

图1 远期利率f(t,T)的定义域PFig.1.Domain P of the forward ratef(t,T).

而量子场,如f(t,T)或A(t,T),本身不能直接观察到,因为它们是波动的,可观察到和测量的是量子场的某些函数的量的平均值,特别地,量子场可测量的量是相关性函数,它表示的是场在某点的波动对场在其他点的波动的影响.更准确地说,场A(t,T)两点的相关性定义为

其中D(T,T′；t)称为传播子(propagator),是场A(t,T)在点(t,T)的波动对A(t′,T′))在另一个点(t′,T′)的波动的影响的度量. δ(t− t′)为狄拉克δ函数,当t̸=t′时,δ(t−t′)=0.

在刚性作用量下的场理论模型下,可推出在远期测度下满足鞅条件的瞬时远期利率的漂移率为

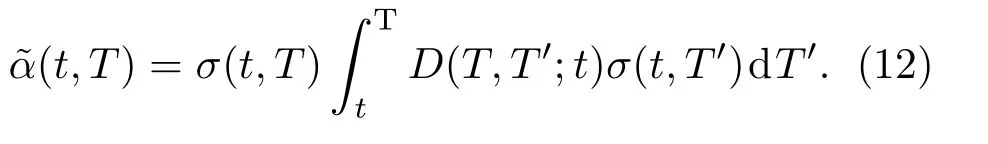
在刚性作用量下的远期利率量子场理论模型中,为了与实证数据进行比较,定义θ=T−t,可得模型的相关性函数

其中

而

3 远期利率的量子场理论模型的构建

由数据的可得性和一致性,我们采用的样本数据是2011年1月4日到2017年12月30日的国债瞬时远期利率的日数据,即1740个瞬时国债远期利率的期限结构,数据均来源于Choice数据库整理,从中选择了0.1年期、0.2年期、0.3年期......9.9年期以及10年期等100个期限的瞬时远期利率数据来进行研究.本研究将样本分成两个子样本,第一个子样本从2011年1月4日到2016年12月30日,共有1490个瞬时远期利率的期限结构,作为模型的估计窗口,利用该子样本内的远期利率数据来选择最优模型并进行参数估计；第二个子样本从2017年1月3日到2017年12月30日,共有250个瞬时远期利率的期限结构,作为模型的预测窗口,对本研究所构建的最优模型的预测能力进行评价.

由于所采用的样本数据是日数据,将时间进行离散化,t=n∗ε,由(6)式表示的远期利率模型可得:

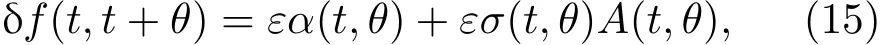
其中,δf(t,t+θ)=f(t+ ε,t+ θ)−f(t,t+ θ),代表新息(innovations),且在后面所有的实证研究中,取时间间隔ε=1 d.

3.1 波动率期限结构和市场相关性结构

在远期利率f(t,θ)的分析中,一个重要的量是δf(t,θ)和δf(t,θ′)之间的相关性, 由(15)式且ε=1,可得δf(t,θ)和δf(t,θ′)的协方差和相关系数分别为(16)和(18)式:

所以,对θ̸=θ′,可得

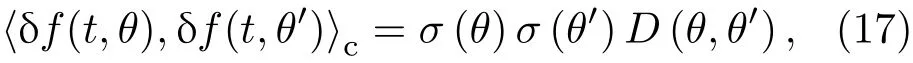
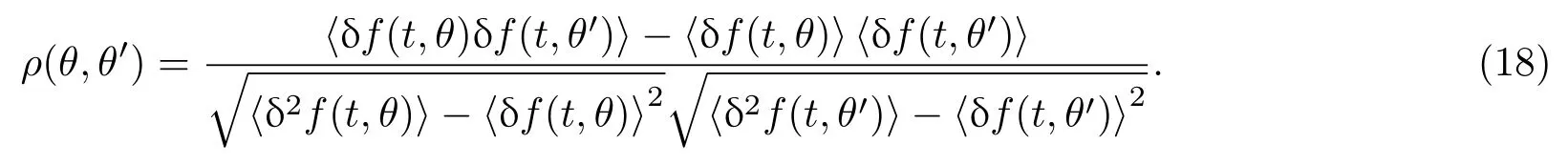
而模型的波动率σ(t,T)=σ(θ)的实证的波动率如下:⟨ ⟩

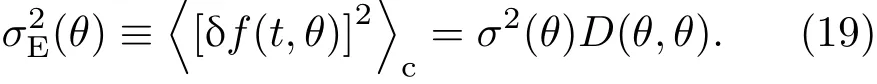
由(19)式可得

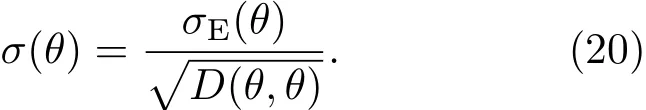
由(17)和(20)式可得

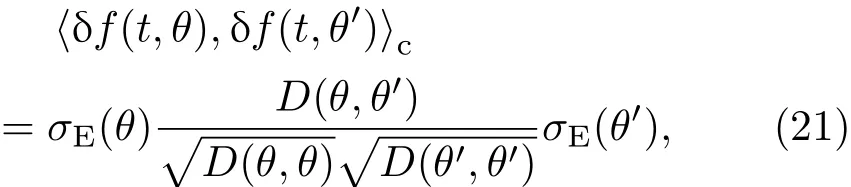
即表明市场的协方差是由实证波动率σE(θ)和模型的标准化后的传播子惟一决定.

而在实证中,实证的波动率可由下式求得(L表示数据的天数):

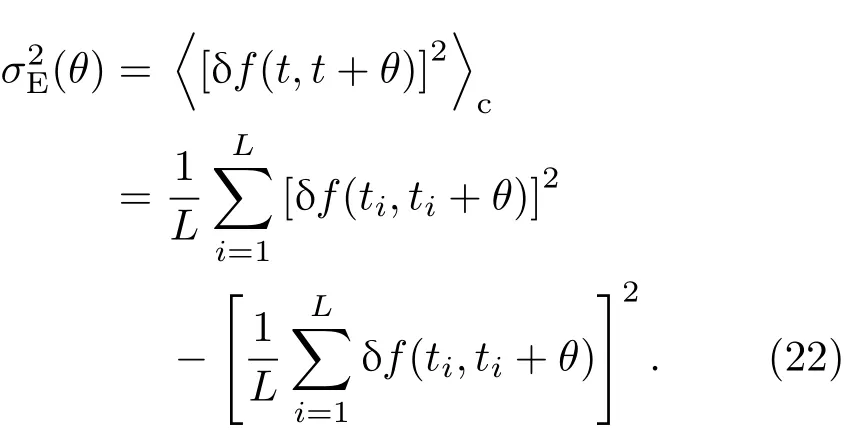
由(17)式可得

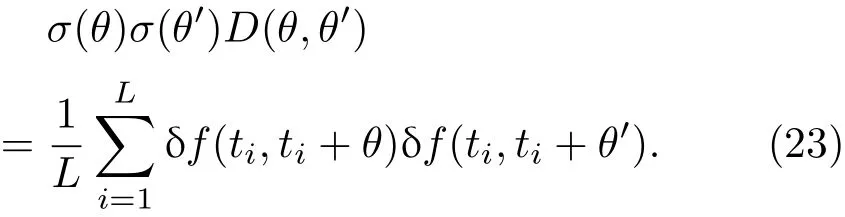
将2011年1月4日到2016年12月30日的样本数据代入(22),(23)和(18)式可分别得到市场上国债远期利率的波动率期限结构和新息的市场相关性结构,分别如图2和图3所示.

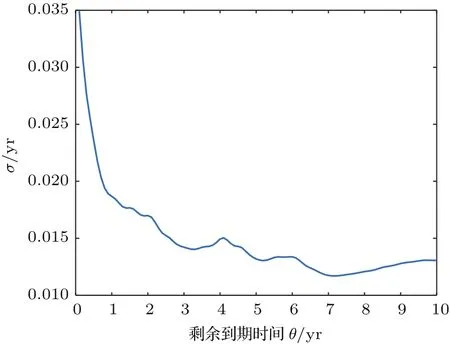
图2 国债远期利率的波动率期限结构Fig.2.Volatility term structure of treasury forward rates.

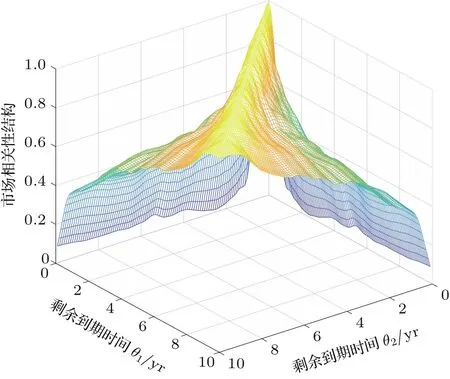
图3 新息的市场相关性结构Fig.3.Correlation structure of the innovations.

由图2可以看出,总体上,我国国债市场的瞬时远期利率的波动率期限结构呈现出缓慢下降的过程,然后在7年左右达到最小值,之后波动率又开始缓慢上升.这说明不同交易日由新的信息所带来的国债瞬时远期利率的波动率以及不同剩余到期时间的波动率增速均受到日历时间t和未来时间T的共同影响,而传统的金融随机过程无法对该性质进行准确的刻画.从图3可以看出,由市场上的各种新的信息引起的不同到期期限的国债瞬时远期利率之间的相关性是不完全的相关性,而传统的金融利率模型即使引入有限个白噪声也无法捕捉到相关性函数的所有信息,而随着模型引入白噪声个数的增加,模型估计难度会显著加大.因而,需要寻求一种能有效纳入这种不完全相关性的新的远期利率模型.

3.2 传统金融上的两因子HJM模型的参数估计

为了验证考虑日历时间和到期时间两个维度上的国债远期利率之间不完全相关性的量子场理论模型的优越性,首先对只考虑日历时间方向上的相关性的传统金融上的HJM模型的拟合结果进行简要说明.

实证中,本文使用国际上应用最广泛的两因子HJM模型,其波动率设定形式如下[30]:

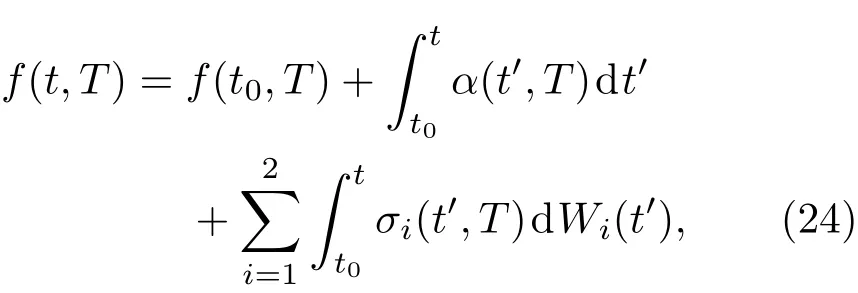
其中σ1(θ)= σ1；σ2(θ)= σ2exp(−γ/2 ∗ θ),θ=T−t.

经过一系列计算后,可得由(24)式表示的两因子HJM模型下的协方差和相关性分别为:

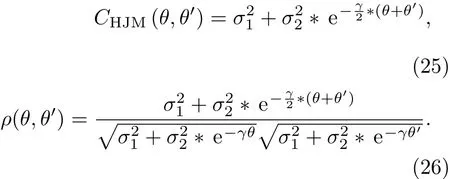
(26)和(18)式提供了模型预测的相关性和市场相关性之间的联系,参数σ1,σ2和γ的值是通过使理论相关性函数与样本期内数据得到的市场相关性函数的均方误差最小而得到的,即基于(27)式来进行参数校准,

研究中,使用非线性函数参数估计的Levenberg-Marquardt法得到参数估计结果列于表1.

表1 两因子HJM模型下参数的最优拟合结果Table 1.Optimal parameters fitting result for twofactor HJM model.

由表1的结果可知,当σ1=0.2682,σ2=2.5279,γ=1.6210时,所得到的两因子HJM模型对国债远期利率的拟合是最优的,因为此时的拟合均方误差最小,约为19.39%,但其对国债远期利率的拟合效果较差,拟合优度R2仅为69.02%,可能原因在于HJM模型只考虑了在日历时间方向上的相关性,而忽略了在到期期限方向上国债远期利率之间的这种不完全相关性.因而,下面将对考虑不同到期期限方向上的国债远期利率之间不完全相关性的量子场理论模型进行研究.

3.3 刚性作用量下的量子场理论模型的参数估计

(13)和(18)式提供了模型预测的相关性和市场相关性之间的联系,参数λ和µ的值是通过使

的理论相关性函数与样本期内数据得到的市场相关性函数的均方误差最小而得到的,即基于(28)式来进行参数校准,

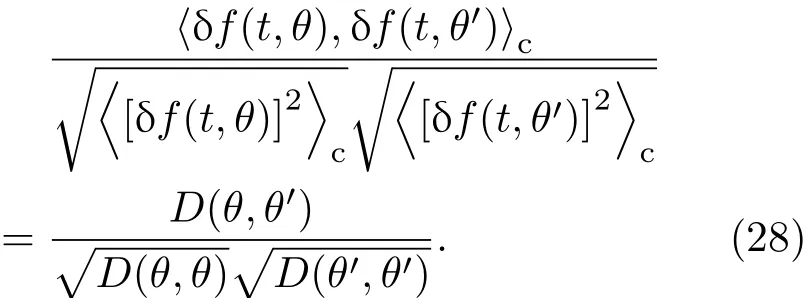
运用非线性函数参数估计的Levenberg-Marquardt法得到参数估计结果列于表2.

表2 刚性作用量下的量子场模型参数的最优拟合结果Table 2.Optimal parameters fitting result for quantum field model based on stif faction.

由表2的结果可知,当λ=3.4015/yr,µ=0.7442/yr,相应的b=3.0371时,所得到的拟合是最优的,整个拟合的均方根误差约为18.59%,而该模型对国债远期利率的拟合优度约为63.23%.

根据数据估计出相关参数后,代入(14)和(13)式即可求出刚性作用量下的量子场理论模型预测的非标准化的刚性传播子和标准化后的相关性结构,如图4和图5所示.

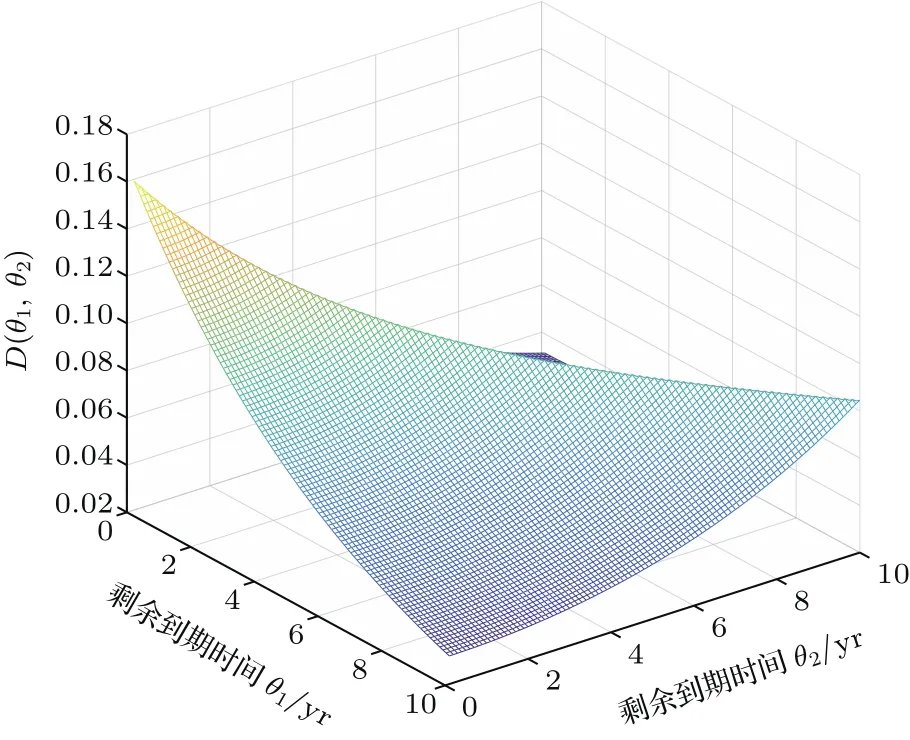
图4 非标准化刚性传播子Fig.4.Non-standardization stif fpropagator.

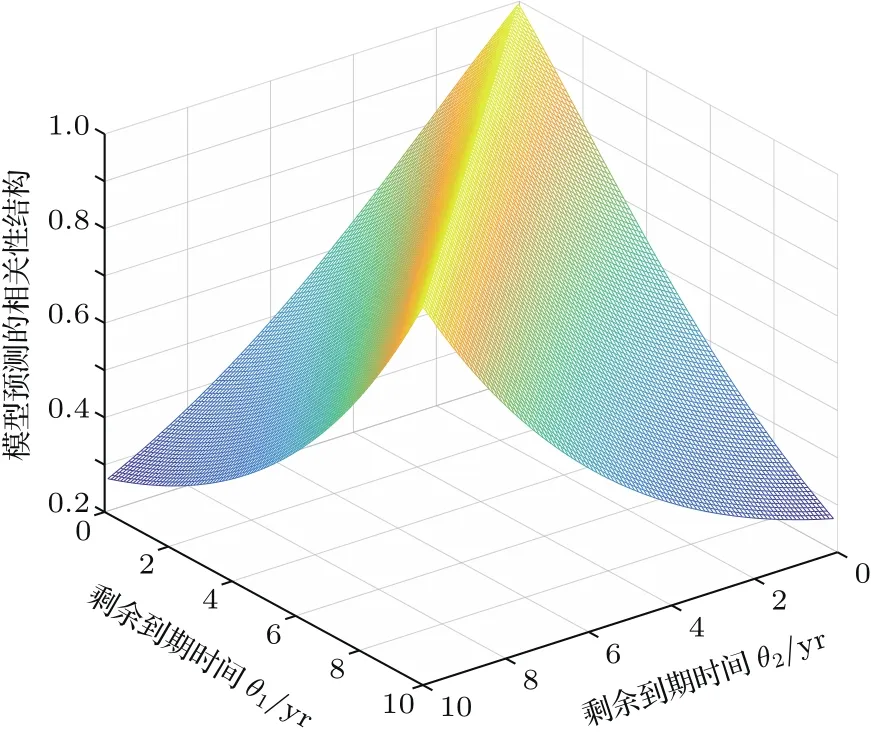
图5 标准化刚性传播子Fig.5.Standardization stif fpropagator.

由表2可知,刚性作用量下的远期利率量子场理论模型对国债远期利率的拟合优度约为63.23%,并没有达到理想的效果.比较图5和图3也可以看出,刚性作用量下的量子场理论并不能对不同到期期限的国债瞬时远期利率的市场相关性结构进行有效刻画.而由于受投资者心理、市场情绪等影响,剩余到期时间对投资者所产生的作用并不像简单的物理时间上的距离那样明显,即两种到期期限的远期利率变化的实际差别并不像由实际的剩余到期时间θ所表现的那样(在物理时间上的距离θ相同,其结果也相同),例如市场参与者通常认为未来10—15年之间的远期利率差异与从当前到5年后之间的远期利率差异是不一样的(但θ均等于5),而这在直观上是合理的,因为对市场参与者而言,距离当前更远的未来的不确定性越大,因而人们感觉到更远的未来的冲击比在较近的未来的冲击在当前更难解决.类似地,在同一时刻,人们所感知的10年后的1年期远期利率的变化可能与1个月后2周期限的远期利率的变化是相似的,这点在3.4节的实证中z(θ)=θv,υ≈0.1142,亦得到了证明.因而,下面试图通过引入人们所感知的剩余到期时间变量z(θ)来提高量子场理论模型的拟合精度.

3.4 引入感知的剩余时间变量后的量子场理论模型的参数估计

引入感知的剩余时间变量z(θ)后,与(13)式类似,模型的相关性函数为

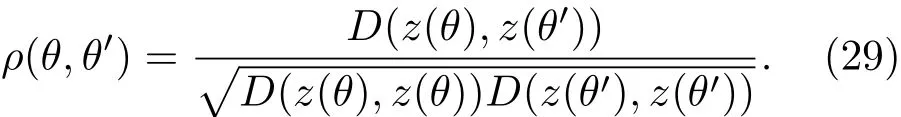
由(14)和(29)式可得

其中z±(θ+；θ−)≡z(θ)±z(θ′).

在文献[20]中表明,在时间θ下,由(13)式表示的归一化相关性模型ρ(θ+,θ−)在θ= θ′处的曲率为

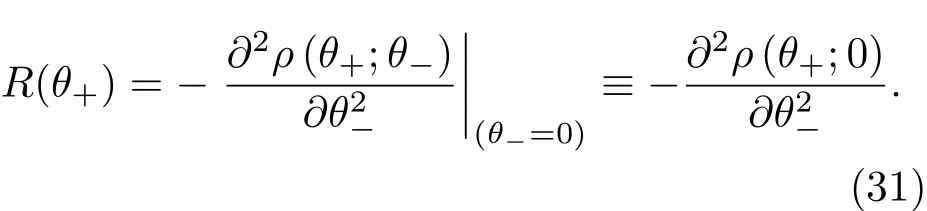
经过一系列计算,最终得到

因而,可得到由(30)式表示的引入心理感知的剩余到期时间变量z(θ)后的归一化相关性模型在θ=θ′的曲率为

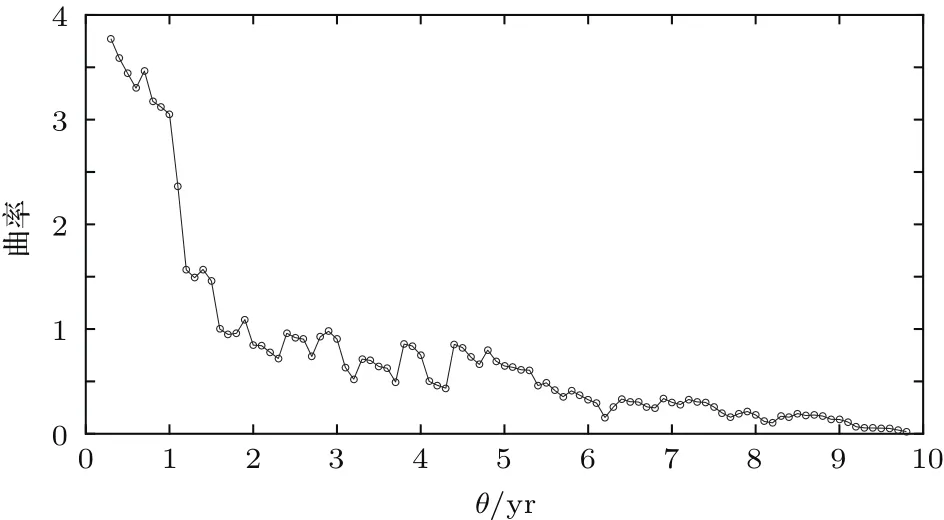
图6 观察到的市场相关性的曲率Fig.6.Curvature of correlations observed in the market.

其中R是时间θ下模型的曲率.由于观察到曲率大致以幂律形式下降(如图6所示),而根据Baaquie[20]的研究结果可知,标准化传播子的曲率变化的形状几乎完全由(33)式中的第一部分[z′(θ+)]2来决定. 因此,z(θ)也应大致是θ的幂函数,故拟设z(θ)= θv来拟合数据,可得到υ≈0.1142.

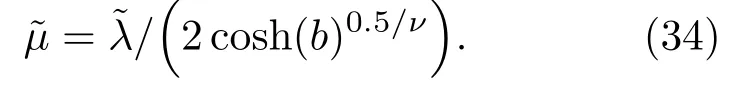
已经利用曲率的市场行为确定γ的值,因此,现在只剩下2个参数ν和µ来拟合整个相关性平面ρ(θ,θ′). 模型的参数估计依然是基于(28)式来进行参数校准,只是将(28)式中的θ用z(θ)= θν来代替,参数估计量多了一个ν,因为z=θv,定义λz=[θ]v和µz=[µ˜θ]v,则在θ是以年来测度的单位内,使用非线性函数参数估计的Levenberg-Marquardt法得到参数估计结果列于表3.

表3 引入z(θ)后的量子场模型参数的最优拟合结果Table 3.Optimal parameters fitting result for quantum field model with z(θ).

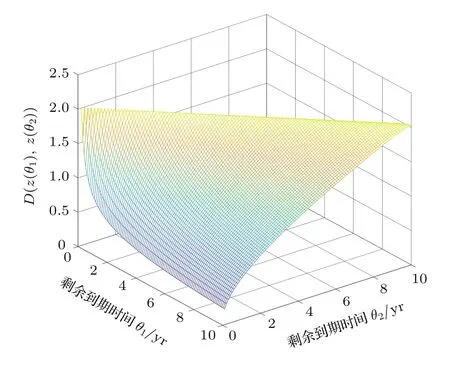
图7 z(θ)下非标准化传播子Fig.7.Non-standardization propagator with z(θ).

图8 z(θ)下标准化传播子Fig.8.Standardization propagator with z(θ).

通过比较图8和图3可看出:两个图形所表示的相关性结构几乎是完全符合的,即图3表示的不完全的市场相关性结构可有效地通过引入心理感知剩余时间变量的量子场理论模型来进行准确刻画.这一方面是由于在远期利率的量子场理论模型中,利用二维量子场有效纳入了国债瞬时远期利率在日历时间和到期时间两个维度上的相关性,相比传统金融上的HJM模型只考虑日历时间方向上的相关性,有效提高了远期利率模型对市场数据的拟合精度；另一方面,心理感知剩余时间变量的引入,囊括了市场情绪、投资者心理等因素的影响,进一步提高了量子场理论模型对数据的拟合效果.

4 最优模型的预测结果分析

由第三节的内容可知,当υ=0.1142,˜λ=28.7300/yr,˜µ=0.0565/yr,相应的b=1.9372时,得到量子场论下国债远期利率的最优模型.在此基础上,通过将量子场A(t,T)离散化,利用最优模型对2017年1月3日到2017年12月30日的0.1年期、0.2年期、0.3年期......9.9年期以及10年期等100个期限的250个瞬时远期利率的期限结构进行样本外预测,将模型预测的远期利率的理论值与实际远期利率进行比较,来对本研究所构建的最优模型的预测能力进行评价.研究中,使用均方根误差(RMSE)和Theil不等系数(U)两个相对指标来进行评价,二者的计算公式如下:

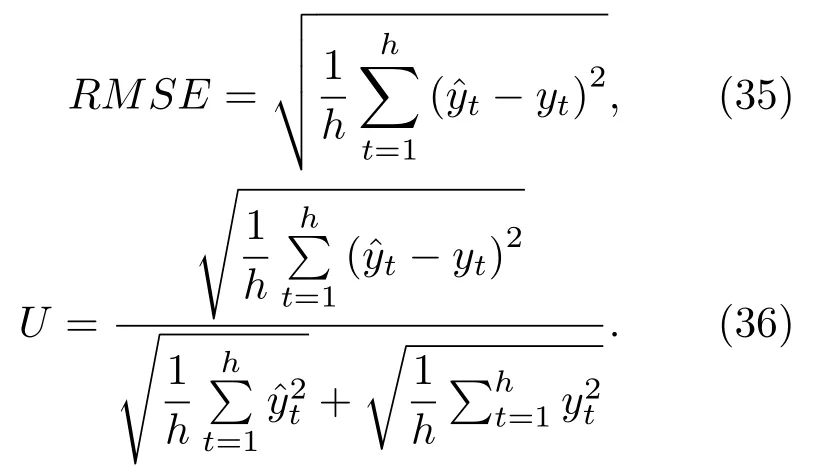
4.1 离散化量子场A(t,T)

由于传播子D(θ,θ′)是个正定对称矩阵, 因而可利用Cholesky分解将传播子D分解为一个下三角矩阵Y及其转置矩阵YT的乘积. 令0 6θ6θM, 其中θM=max(T−t), 对传播子D(θ,θ′)进行Cholesky分解可得

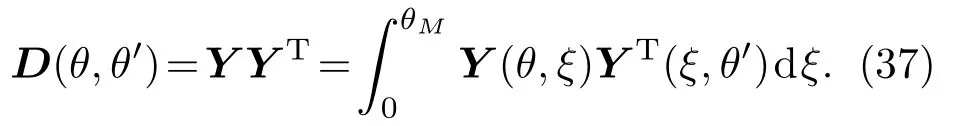
对于θ=T−t,令

其中E[R(t,ξ)R(t′,ξ′)]= δ (t−t′)δ(ξ−ξ′),R(t,ξ)是每个日历时间t和未来剩余时间ξ所对应的独立高斯随机变量.当i,j为离散整数时,根据狄拉克-δ函数可得

因此,当未来剩余时间ξ=ξ′时,由上式可得:

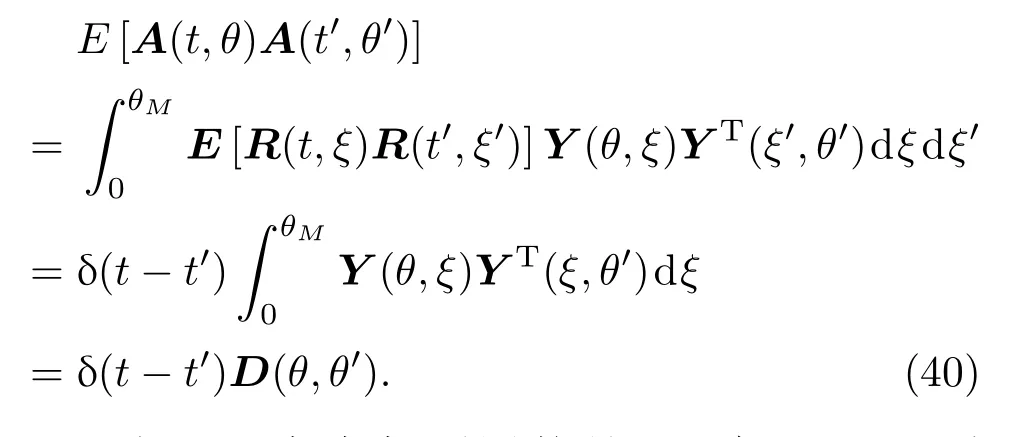
由于研究中想预测的是2017年1月3日到2017年12月30日期间的0.1年期、0.2年期、0.3年期......9.9年期以及10年期等100个期限的瞬时远期利率,共250个瞬时远期利率的期限结构,因而在实证中,以2016年12月30日的远期利率期限结构作为初始的远期利率期限结构.此外,设t0=0年,将日历时间t和剩余到期时间θ离散化为:

其中,εt=1,2,...,250,j=1,2,...,100.

则 量 子 场A(t,θ)和 远 期 利 率f(t,θ)重 新表示为

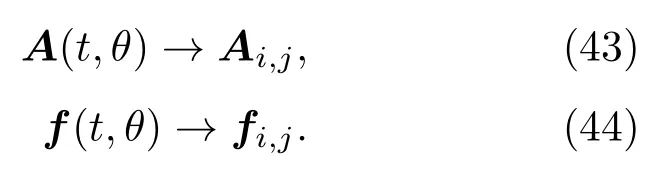
由远期利率推导公式可以得到:

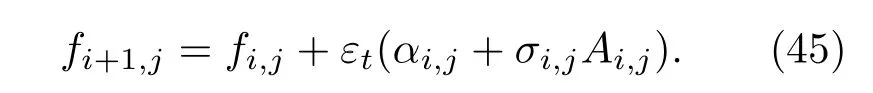
则离散化下的剩余未来时间θ=j∗εθ,θ′=j′∗εθ,(38)式可重新表示为

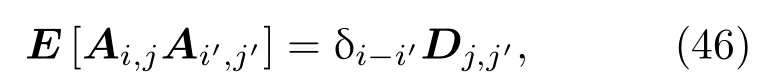
其中,i,i′=1,2,...,250,j,j′=1,2,...,100.则由(37)式可得:

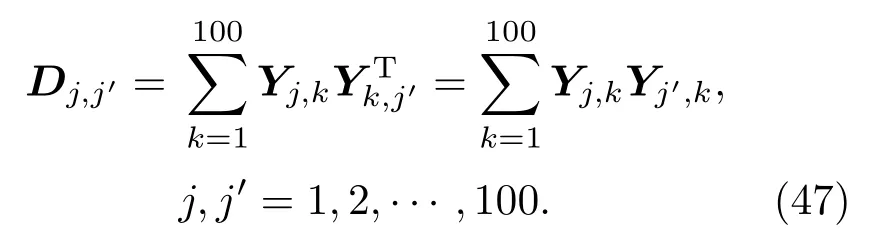
因而,量子场Ai,j可以通过(48)式得到

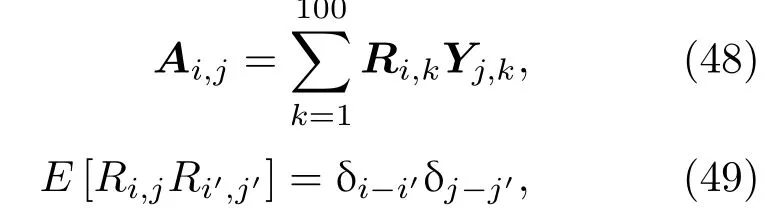
其中,Ri,j是方差为的高斯随机变量,即

根据连续时间下漂移率α˜(t,T)的(12)式可推出,离散时间下漂移率满足下列条件:

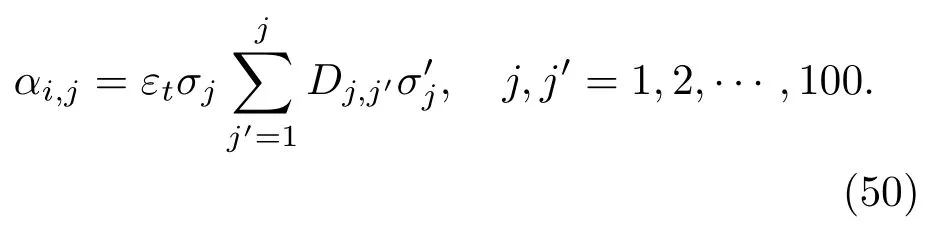
因而可得,国债瞬时远期利率的更新方程如下:

4.2 稳健性检验

为了对模型的稳健性进行检验,将引入感知的剩余时间变量z(θ)得到的最优远期利率量子场理论模型的参数估计结果代入所得到的传播子进行Cholesky分解,利用Matlab对(48)式中的Ri,j模拟10000次并对模拟得到的10000次结果取平均值,最后将所有参数代入由(51)式表示的远期利率更新方程即可得到2017年1月3日到2017年12月30日期间的0.1年期、0.2年期、0.3年期......9.9年期以及10年期等100个期限的瞬时远期利率的250个瞬时远期利率的期限结构结果.

为了将考虑日历时间和到期时间两个维度相关性的远期利率的量子场理论模型的预测效果与传统金融上只能考虑日历时间方向上的相关性的两因子HJM模型进行比较,将(24)式表示的两因子HJM模型进行离散化,可得其利率更新方程:

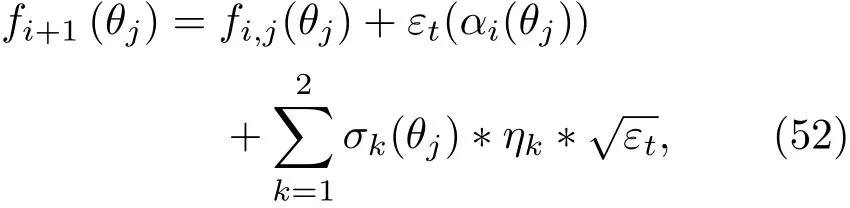
其中ηk表示相互独立的高斯白噪声,且αi(θj)和σk(θj)满足(53)式,

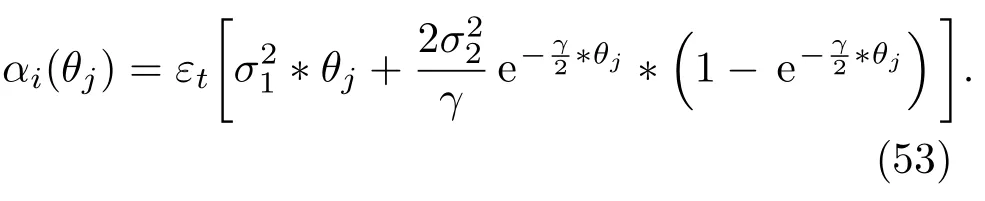
将最优估计参数σ1=0.2682,σ2=2.5279,γ=1.6210代入(53)式可得到本文所设定的两因子HJM模型下的漂移项,利用Matlab对(52)式中的ηk(k=1,2)模拟10000次并对模拟得到的10000次结果取平均值,最后将所有参数代入由(52)式表示的远期利率更新方程,即可得到2017年1月3日到2017年12月30日期间的0.1年期、0.2年期、0.3年期......9.9年期以及10年期等100个剩余到期期限的瞬时远期利率的250个瞬时远期利率的期限结构结果.

图9给出了最优量子场理论模型和传统两因子HJM模型预测的100个剩余到期期限的平均瞬时远期利率期限结构图,而图10和图11则分别给出两个模型预测的各期限瞬时远期利率的均方根误差(RMSE)和Theil不等系数(U)的图形.

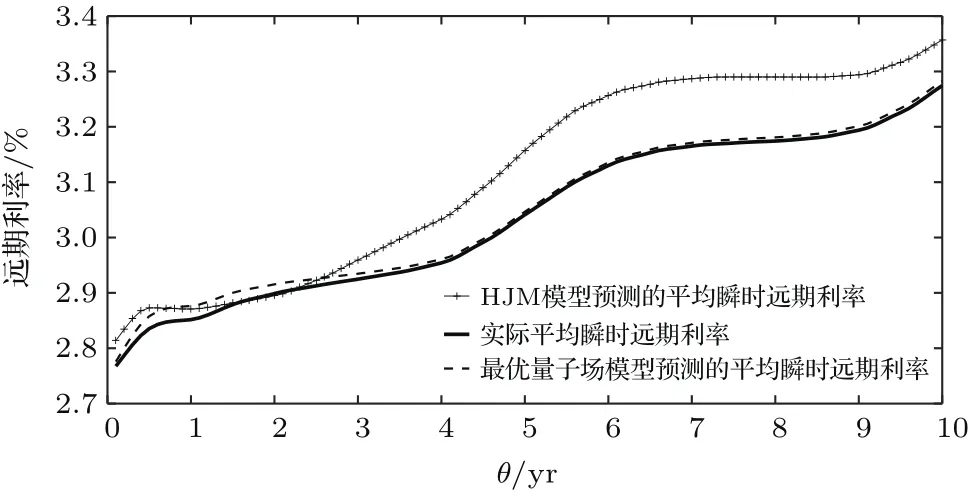
图9 平均瞬时远期利率期限结构图Fig.9.Average instantaneous forward rate term structure.

由图9可知,平均而言,在剩余到期期限θ小于2.3年时,利用最优量子场理论模型模拟得到的平均瞬时远期利率期限结构存在一定的误差,而当θ大于2.3年以后,二者几乎重叠在一起.此外,当θ较小时,最优量子场理论模型与HJM模型预测的平均瞬时远期利率差异较小,但随着θ的不断增大,二者的差值在不断增大.而图10和图11的两个指标均直接证实了同时考虑日历时间和到期时间两个维度的相关性的量子场理论模型大大提高了远期利率模型的精度,因为对量子场理论模型预测的任意剩余到期期限θ的瞬时远期利率,其均方根误差(RMSE)和和Theil不等系数(U)均小于相对应的HJM模型的预测值.这主要是由于远期利率的量子场理论模型是直接对远期利率的实际市场演化进行建模,模型所需估计的参数均直接由市场数据拟合得到,无需对波动率的函数形式做任何假定,而由市场得到的确定性波动率大幅度提高了量子场理论在金融应用上的准确性,而不像传统金融上的HJM模型,需要事先对波动率的函数形式进行设定.

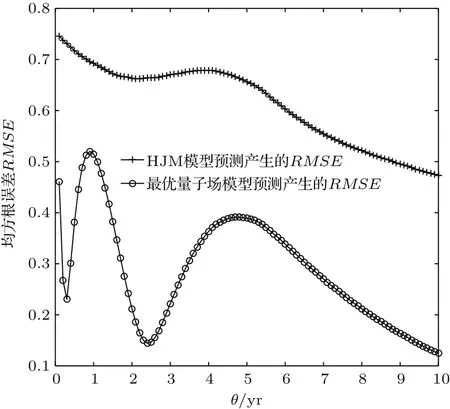
图10 预测的各期限瞬时远期利率的RMSEFig.10.RMSE of instantaneous forward rates predicted.

图11 预测的各期限瞬时远期利率的UFig.11.U of instantaneous forward rates predicted.

5 结 论

传统金融上使用的绝大多数的远期利率模型均是HJM模型的推广,而由于传统随机微积分存在着提高模型精度与简单模型之间的固有矛盾,使得当前主流的HJM模型无法对实际金融市场中不同到期期限的远期利率的不完全相关性进行准确刻画.而利用量子场理论来对远期利率期限结构的动力学过程进行建模的背后直觉来自于:每个不同到期期限的国债远期利率既随机演化又不与其他到期期限的远期利率完美相关,在每一个场理论模型中,无限个因子是通过一个支配不同到期期限的远期利率之间的相关性的函数(即场理论模型中的传播子算符)来关联.此外,本文所构建的量子场理论模型产生于有限因子HJM框架,将HJM模型中只依赖于日历时间t的布朗运动用一个既依赖于日历时间t又依赖于到期时间T的二维量子场来代替,另一方面,相比传统金融的HJM模型,国债远期利率的量子场理论模型适用性更强,特别地,无需对波动率的函数形式做任何假定,由市场得到的确定性波动率大幅度提高了量子场理论在金融应用上的准确性.

实证研究结果亦表明,所构建的考虑日历时间和到期时间两个维度上的相关性后的远期利率量子场模型所得到的结果与观察到的远期利率的市场行为更符合,尤其在引入心理感知剩余时间变量后的量子场理论模型下,远期利率的量子场理论模型对国债远期利率市场行为的拟合优度超过92%,远优于传统金融上只能考虑日历时间方向上的相关性的两因子HJM模型69.02%的拟合优度.此外,通过对传播子进行Cholesky分解,离散化量子场,并将估计所得的最优参数代入最优量子场理论模型下的远期利率更新方程,进行样本外预测.从平均瞬时远期利率、均方根误差(RMSE)和Theil不等系数(U)三个方面的结果均直接证实了同时考虑日历时间和到期时间两个维度的相关性的量子场理论模型对国债远期利率期限结构建模的优越性.

本文的实证结果,一方面对有关国债远期利率的实证研究具有重要意义,因为一个精确的远期利率模型可有效提高相关的以国债为标的的各种金融产品定价的准确性.另一方面,从金融理论方面来看,场理论方法确实为研究和理解资本市场的动力学特征增加了新的思路.