超高精度空间站共视时间比对新方法∗

刘音华 李孝辉

1)(中国科学院国家授时中心,西安 710600)

2)(中国科学院大学,北京 100049)

(2018年4月27日收到；2018年6月25日收到修改稿)

1 引 言

目前广泛应用的导航卫星共视时间比对技术可以实现3—5 ns的时间比对精度,但星载原子钟的性能和时间比对链路的误差特性限制了比对精度的进一步提高.随着科技的发展,纳秒级的时间比对精度已经不能满足许多基础前沿研究的需要,例如精细结构常数测量、引力红移测量等基础物理实验,对时间比对精度提出了更高的要求[1−5].目前可实现的精度最高的时间比对技术基于光纤链路,其精度能达到几十皮秒甚至皮秒量级[2,6,7],但这是以光纤物理链路为前提的,存在较大的应用局限性.

我国正在大力建设的载人航天空间站和欧洲ACES(Atomic Clock Ensemble in Space)空间原子钟组计划,本文把两个系统统称为空间站,在空间站上均搭载高精度原子钟组,空间原子钟在近地微重力环境下具有比地面原子钟更好的性能[8−11],形成周期性覆盖全球的最高稳定度的时间系统.利用空间站对地的高性能微波时间比对链路,可以实现基于空间站的超高精度共视时间比对[12−16].

空间站共视时间比对技术类似于导航卫星共视时间比对,但两者存在一定的差别.首先,空间站运行在近地环境下,轨道高度低,运行速度快,可视时间短[9,10,12,13],每天只能在极少数的时间内利用空间站进行共视时间比对,部分地面站不满足同时可视空间站的条件,尚不能进行共视比对.而导航卫星数目多,且包含有全天可视的GEO(Geosynchronous Earth Orbit)卫星[17−19],利用导航卫星可进行实时共视时间比对.其次,对于共视时间比对技术而言,轨道误差对时间比对的影响与轨道高度成反比,导航卫星共视中完全可以忽略轨道误差的影响,但轨道误差是空间站共视的主要误差源,不能忽略.再次,导航卫星共视的精度在纳秒量级,许多百皮秒量级或者更低的精细误差不用考虑,空间站共视的目标是实现几十皮秒精度的时间比对,需要以更精确的理论框架——广义相对论为基础来考虑皮秒级别以上的所有误差源.鉴于此,不能直接利用传统的共视时间比对原理开展空间站共视时间比对,需要提出适用于空间站特性的共视时间比对新方法.

目前空间站共视时间比对在国内外都属于预先研究领域,本文打破传统实时共视的常规,提出空间站分时共视时间比对的新方法,一方面解决空间站地面可见性带来的共视盲区问题,另一方面很好地修正了空间站轨道误差带来的影响.通过仿真实验对所提方法进行了验证,可以在地面站间实现几十皮秒精度的共视时间比对.

2 空间站共视时间比对原理

利用空间站高精度原子钟作为参考源,实现两地面站间的高精度共视时间比对.由于空间站原子钟与地面站钟都处于地球引力场中,要想实现几十皮秒量级的比对精度,必须要以广义相对论的时间比对理论作为基础来建立数学模型[11,12,20−22],充分考虑地球引力时延的影响,才能达到预期的时间比对精度.在广义相对论地心非旋转坐标系GCRS(Geocentric Celestial Reference System)中,介绍空间站与两地面站之间的共视时间比对原理.

假设地面站A和B在t0时刻接收到空间站的时间比对信号,两地面站与空间站的钟差可以表示为:

其中,∆TAS和∆TBS分别为两地面站与空间站的钟差,PA和PB为两地的观测量,ρSA和ρSB为空间站和地面站之间的距离矢量,c为光速,νA和aA分别为地面站A在地心非旋转坐标系中的速度和加速度矢量,νB和aB分别为地面站B在地心非旋转坐标系中的速度和加速度矢量,τ和τ为电离层延迟,和为对流层延迟,其余为与相对论有关的时延. ρSA.νA/c2和ρSB.νB/c2为Sagnac效应产生的影响,代入400 km的轨道高度和地球自转线速度,可以粗略估计该项影响为10 ns量级.

为地面站速度的二次幂和加速度的影响,同理可以估算其影响在0.1 ps以下.两式右边倒数第二项为夏皮罗时延,G为牛顿引力常数,ME为地球质量,rS和rA,rB分别为空间站和地面站到地心的距离,影响为10 ps量级.

(1)和(2)式右边最后一项为坐标时到两地面站原时之间的转换时延,是广义相对论中需要考虑的时间坐标转换量.根据广义相对论时空间隔与度规张量的关系,忽略高阶项的影响,地面站原时与坐标时的关系表示为:

(5)和(6)式中,TSA和TSB分别为信号从空间站到两个地面站之间传输延迟,包括(1)和(2)式右边括号中除和以外的所有延时项.因此,可以粗略估计和的数量级在皮秒量级.

忽略(1)和(2)式中量值在皮秒以下的部分,两式相减可以得到两站共视时间比对的表达式,如(7)式所示.

从(7)式可以看出,两站的共视时间比对其实是各项延迟之间的差分运算,通过差分可以抵消两站的共有误差,改善时间比对的精度.但是共视时间比对要求两个地面站同时获取观测量,才能以空间站原子钟作为媒介计算地面站间的钟差.

3 传统共视方法的应用局限

(7)式是考虑了皮秒级精细误差的空间站共视时间比对公式,是基于传统的共视方法推导得来,直接应用于空间站共视时间比对存在一定的局限性.

3.1 空间站可见性导致的应用盲区

空间站运行在近地环境下,轨道高度大约为400 km,平均轨道周期大约为1.5 h,一天可视的飞行周期大约为9个,每个轨道周期对于单个地面站的平均可视时间非常短,大约在400 s左右,因此每天只能在极少数的时间内利用空间站进行时间比对.另一方面,鉴于对地面接收信号质量的考虑,一般会利用高度角来对空间站数据进行筛选,很多文献利用高度角大于10◦作为数据筛选条件,这势必导致空间站有效的可视时间进一步缩短.因此,如果利用空间站进行两个地面站的共视时间比对,对空间站的可见性要求更加苛刻,按照共视比对原理,要求两个地面站同时可视空间站,这将使能进行比对的时间进一步减少,部分地面站之间由于不存在同时可视空间站的时刻而存在共视时间比对的盲区.

利用卫星工具软件STK(satellite tool kit)来对我国载人航天空间站的轨道进行建模,对中国几大主要地理城市进行空间站的可见性仿真分析.

具体的仿真过程概述如下:首先,新建一个STK软件的仿真工程,仿真时长设置为1 d,在“object browser”菜单中的“satellite”功能项中建立空间站模型,按照图1所示参数对空间站轨道进行建模,主要参数包括近地点和远地点的轨道高度、轨道倾角和升交点的经度；接着通过“object browser”菜单中的“facility”功能项添加地面城市,通过“properties”选项设置各地面城市的坐标；然后,在“analysis”菜单中选择“access”选项,在弹出的图2所示界面中设置需要进行可见性分析的地面城市,例如图中设置的是进行长春的可见性分析,也可以通过“select object”选项选择其他城市.最后,点击图2中的“compute”按钮,进行可见性计算,通过“reports”和“graphs”下面的“access”按钮分别可以获取该地面城市对空间站一天内的可见时段分析数据和分析图.

本文以高度角为10◦作为下限条件,对北京、长春、漠河、西安、喀什、昆明、拉萨、上海和三亚等城市进行了空间站的可见性分析,分析时间长度为1 d.汇总各城市在1 d内对空间站的可见时段数据绘图,如图3所示,图中横坐标为1 d的分钟累计数,其数值范围为[1,1440],由于700 min之前空间站还没有入境,所以图中横坐标起始点从700开始.从图中可以看出,每个城市每次的可见时段都非常短.通过对绘图原始数据进行分析可知,每个城市平均每次可视空间站的时长约为4 min.漠河在中国最北方,每天对空间站的有效观测时段只有一个,大约为4 min.其余城市,不论是西北部的喀什,东北的长春,东部的上海,西部的拉萨,还是南部的三亚和昆明,每天可见的空间站轨道周期数目至少有3个.

图1 空间站建模轨道参数Fig.1.Orbit parameters of space station modeling.

图2 STK软件中空间站可见性分析界面Fig.2.Space station visibility analysis interface in STK tool.

图3 中国几大地理城市对空间站的可见时段(高度角＞10◦)Fig.3.Visibility of main geographical city in China(elevatio＞10◦).

对图3在800 min附近的那个空间站轨道周期进行放大,如图4所示,可以清楚地看出在该周期各城市对空间站的可见性.由图4可见,在该周期内,空间站对漠河和喀什不可见,其他城市的可见时段并不同步且时间长短也不相同.不同的两个地面站对空间站同时可见的时间长度也不相同.三亚和拉萨同时可见空间站的时长最长达6 min,昆明和北京只有1 min的同时可见时间.尽管长春和西安在该轨道周期均有可视时间段,但这两个城市没有有效的同时可见空间站的时段.因此,在该轨道周期内各地面站间进行空间站共视时间比对的时长并不相同,还有些站之间因为没有同时可见时段不能进行传统的共视时间比对,例如长春和西安、喀什和其他各站、漠河和其他各站等.

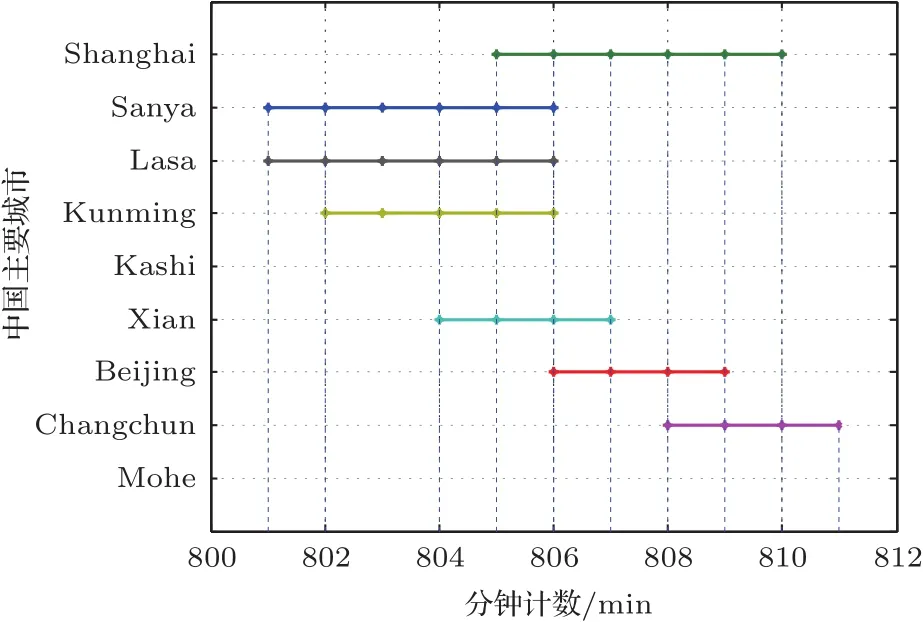
图4 单个轨道周期各城市的可见性(高度角＞10◦)Fig.4.Visibility of main geographical city in one orbit period(elevatio＞10◦).

综合各个轨道周期的可见性仿真结果可知,各站之间每次进行传统共视时间比对的时长非常短,平均在3 min左右,每天也就在十几分钟左右.还有些站之间不能进行传统共视时间比对,例如喀什和西安、三亚,长春和昆明、三亚,漠河和三亚、拉萨等.因此,鉴于空间站对地可见性特点,传统的实时共视时间比对方法存在一定的应用盲区.

3.2 空间站轨道误差导致共视精度受限

(7)式中忽略其他项的影响,等号两边对空间站位置求导,可得到

对上式进一步转换,可以得到

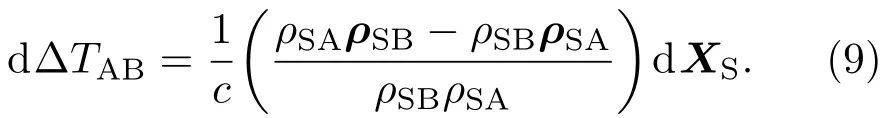
假设ρSA=ρSB+∆ρ,则有

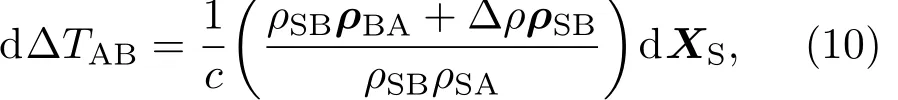
ρBA为地面站A与地面站B之间的基线矢量.因此,可以得到

进一步化简,得到

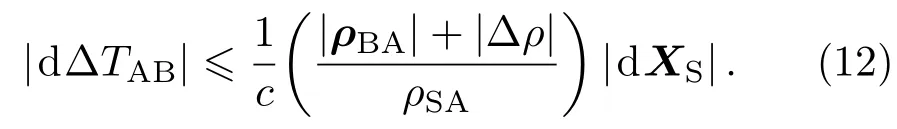
由(12)式可知,空间站轨道误差对共视时间比对的影响与空间站与地面站的几何距离、两地面站之间的基线长度和轨道误差本身的大小有关.空间站上搭载高性能GNSS(Global Navigation Satellite System)接收机,用于实时提供空间站轨道信息.随着全球卫星导航系统的建设与发展,目前GNSS接收机定位精度已达到分米甚至厘米量级.有研究表明,GPS接收机曾搭载在地球低轨飞行器上,提供了优于10 cm的轨道位置服务[23−25].空间站与地面站的几何距离可近似用轨道高度来估计,轨道高度大约为400 km,如果两地面站之间的基线长度大于400 km,空间站轨道误差会得到放大.利用空间站进行远距离的共视时间比对,基线长度一般都会大于轨道高度.对于基线长度为2000 km的共视时间比对,轨道误差按10 cm估算,其对两地时间比对的影响可达纳秒量级,这对精度为几十皮秒量级的时间比对来说影响是巨大的.

结合空间站1 d的运行轨道,把空间站在径向R、切向T和法向N(RTN)三个维度的轨道误差均设置为0.1 m,地面站设置为西安和长春,对轨道误差对传统共视时间比对的影响进行仿真,轨道误差引起的共视时间比对误差仿真结果如图5所示,图中横坐标为1 d的秒累计数,其数值范围为[1,86400],由于西安和长春只在35000—60000 s之间有传统共视比对的数据,所以图中横坐标范围为[35000,60000].从图5可以看出,1 d中不同的时刻轨道误差对传统共视时间比对的影响量并不相同,RTN三个方向各0.1 m的空间站轨道误差对西安和长春共视时间比对造成的影响最大可为850 ps,最小为550 ps左右,引起的共视时间比对误差波动范围达到了300 ps左右.因此,空间站轨道误差不仅对传统共视时间比对的影响数值较大,还会引入百皮秒量级的误差波动.经过分析发现,RTN三个方向各0.1 m的空间站轨道误差在不同的时刻对共视比对的影响值不同,是由于在不同的时刻空间站与两个地面站的相对位置关系并不相同,确切地说是空间站与两个地面站间的视线方向与RTN三个方向的夹角一直在随时间发生变化,导致轨道误差在两个地面站视线方向的投影一直在发生变化,从而使不同时刻轨道误差对共视时间比对的影响不相同.空间站与两个地面站的相对位置关系对共视时间比对的影响将在下面详细分析.

图5 RTN 0.1 m轨道误差引入的共视时间比对误差Fig.5.Common-view time comparison error caused by orbit error of RTN 0.1 meters.

因此,通过上述理论分析和仿真实验,均可以看出轨道误差对空间站共视时间比对的影响是巨大的,采用传统的共视时间比对方法不能实现几十皮秒精度的时间比对.

4 空间站共视时间比对新方法

从前面的分析可知,传统的共视时间比对方法不能直接应用于空间站共视比对,一方面存在应用的盲区,另一方面由于轨道误差的影响也不能实现几十皮秒量级的超高精度时间比对.为了克服上述困难,本文提出了适用于空间站轨道特性的共视时间比对新方法——分时共视法.

4.1 分时共视方法的工作原理

图6为空间站(设为S)与两个地面站(站A和站B)之间的位置关系示意图.αSA,βSA,γSA分别为空间站与地面A站之间的矢量与轨道径向、切向和法向之间的夹角.

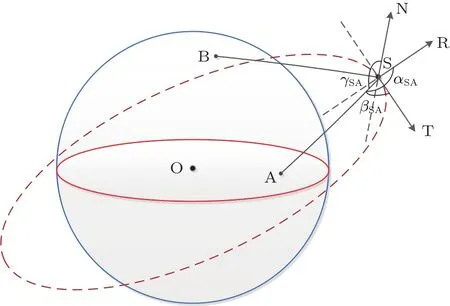
图6 空间站与地面站之间的位置关系示意图Fig.6.Position relationship between space station and ground stations.

空间站轨道误差对于地面站A单向时间比对的影响可以表示为

式中dX,dXdX分别为空间站轨道误差的径向、切向和法向分量,dSA为轨道误差对空间站与地面站A钟差的影响量.

同理,可以推导出轨道误差对于地面站B单向时间比对的影响表达式:

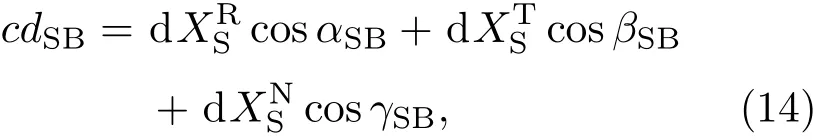
式中αSB,βSB,γSB分别为空间站与地面B站之间的矢量与轨道径向、切向和法向之间的夹角,dSB为轨道误差对空间站与地面站B钟差的影响量.

因此,结合(13)和(14)式,可以得到空间站轨道误差对共视时间比对的影响,表示为

从(15)式可知,如果空间站与地面A站之间的矢量与轨道RTN三个方向之间的夹角余弦值与空间站与地面B站之间的矢量与RTN三个方向之间的夹角余弦值符号分别相同且大小分别相当,则(15)式右边三项误差基本能够得到抵消,这样就能满足超高精度共视时间比对的要求了.因此,可以利用两地面站和空间站的相对位置关系,在两地与空间站满足特定位置关系时进行观测,这时轨道误差的相关性最高,利用共视原理可以抵消大部分轨道误差的影响.本文采用(16)式作为判决条件,来寻找符合要求的空间站与两个地面站的相对位置关系.

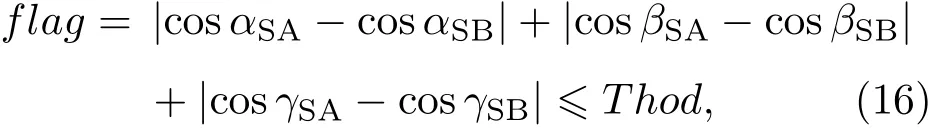
(16)式中,flag为判决因子,Thod为判决门限,通过判决门限来调整轨道误差对两个地面站间时间比对的影响量.例如空间站在RTN三个方向轨道误差均小于0.1 m,判决门限设置为0.03可以使轨道误差对时间比对的影响小于10 ps.需要注意的是,判决门限并不是越小越好,判决门限越小,满足(16)式限制条件的两个地面站的观测时刻越少,需要综合权衡来设置适当的判决门限.

所谓分时共视,即两个地面站并不同时获取空间站的观测量,例如地面站A在t1时刻采集观测数据,地面站B在t2时刻采集观测数据,地面站A在t1时刻、地面站B在t2时刻与空间站的位置关系满足(16)式的判决条件,则地面站A在t1时刻通过单向时间比对原理解算的A站与空间站的钟差∆TAS(t1)和地面站B在t2时刻解算的B站与空间站的钟差∆TBS(t2)中包含的空间站轨道误差分量几乎相当,对∆TAS(t1)和∆TBS(t2)进行差分运算,可抵消空间站轨道误差的影响.

但由于两个原子钟之间的相对频率偏差会使其相位偏差随着时间发生变化,不能直接对∆TAS(t1)和∆TBS(t2)相减计算A,B两站的钟差,必须获取同时刻的两个地面站与空间站的钟差才能计算两个地面站的钟差,这是共视时间比对原理的根本.

由于空间站原子钟具有高于地面原子钟的稳定性,秒级稳定度优于10−13,天稳定度优于10−15,需要进行几十皮秒超高精度时间比对的地面站原子钟也具有很好的频率稳定性,频率漂移可以忽略不计.因此,可以采用一次多项式对地面站与空间站的解算钟差进行建模,得到相对频率偏差.钟差模型如(17)式所示:

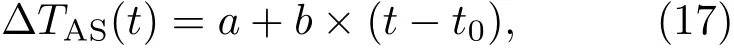
式中,a为常数项；b为一次项系数,即相对频率偏差,为目标参数；t0为模型起点.

然后可以通过(18)式外推得到地面A站在t2时刻与空间站的钟差∆T(t2).

获得了两地同时刻相对于空间站的钟差之后,可以通过下式计算两个地面站之间的钟差:

由于∆TAS(t1)和∆TBS(t2)中包含的空间站轨道误差分量几乎相当,在(19)式中抵消了空间站轨道误差的影响,至此实现了分时共视时间比对.

从(17)式可知,钟差建模是基于单向时间比对原理解算的地面站与空间站的钟差数据进行的,该数据包含有空间站轨道误差的影响,所以会存在一定的建模误差.忽略其他误差的影响,只考虑空间站轨道误差和建模误差,图7定性地展示了分时共视轨道误差的抵消过程.地面站A在t1时刻、地面站B在t2时刻与空间站的位置关系满足(16)式的判决条件,则A站t1时刻解算钟差中包含的轨道误差和B站t2时刻解算钟差中包含的轨道误差几乎相当,为εor,分别如图7中A,B两点所示.A站经过建模外推获得其在t2时刻与空间站的钟差,该钟差值除包含原有的轨道误差以外还增加了建模误差εmod,如图中A′点所示.最后的时间比对是在A′点和B点开展的,通过共视原理抵消了轨道误差εor,只保留了建模误差εmod.本方法巧妙地通过建模获取钟差的线性化变化参数,即使钟差解算值轨道误差较大,但建模误差导致的最终时间比对误差却远远小于原始轨道误差带来的影响.第5节将通过仿真实验来进行验证.

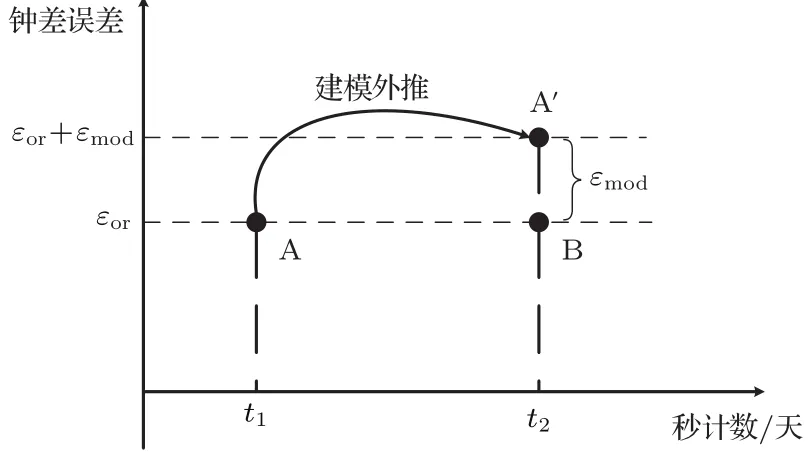
图7 分时共视轨道误差抵消过程Fig.7.Orbit error canceling course of asynchronous common-view time comparison.

4.2 分时共视方法的优势

从分时共视的工作原理可知,本方法的理论根本还是(7)式,即通过获取两个地面站同时刻与空间站之间的钟差,然后再利用共视原理抵消轨道误差和其他共有误差的影响.但是两个地面站同时刻与空间站之间的钟差并不都是通过观测量解算得来,一个地面站的钟差通过观测量直接计算获得,另一个地面站的钟差通过建模外推获得.分时共视方法充分利用了空间站原子钟和地面站原子钟的高稳定性,通过钟差建模外推既解决了共视原理要求的两地同时刻钟差的差分计算,也极大程度地抵消了空间站轨道误差这一主要误差源的影响,结合(7)式各项精细误差修正,可以实现几十皮秒精度的时间比对目标.

另一方面,由于分时共视方法并不要求两个地面站同时可视空间站,可以用于传统共视方法的应用盲区.例如,喀什和西安不满足同时可视空间站的条件,则不能按照传统共视方法进行时间比对.但是,喀什和西安满足上述分时共视的条件,可以利用分时共视方法进行时间比对.

此外,分时共视方法基于空间站的无线电信号进行时间比对,是基于自由空间的时间比对方法,不用铺建时间比对的物理链路,比光纤时间比对技术具有更广泛的应用范围.

5 新方法的仿真验证

为了验证上述空间站分时共视时间比对方法的有效性,开展了地面站间分时共视时间比对的仿真实验.

5.1 西安-长春分时共视仿真实验分析

西安和长春的时间比对基线长约2000 km.在进行分时共视时间比对仿真之前,首先对西安和空间站的原子钟差、长春和空间站的原子钟差进行仿真.西安原子钟的秒级稳定度设为10−13,天稳定度设为10−15,长春原子钟的秒级稳定度设为5×10−12,天稳定度为3×10−14.然后进行两个地面站观测量的仿真,观测量包含空间站与地面站的几何距离、电离层延迟、对流层延迟、夏皮罗延迟等各项延迟分量.电离层延迟的仿真利用IGS网站发布的垂直电离层电子含量网格文件,电离层延迟的解算采用双频观测量组合计算方法.对流层延迟利用Saastamoinen模型建模仿真,气象参数仿真条件:温度T=298 K,气压P=1 bar,水汽压e0=0.5 bar.空间站在RTN三个方向的轨道误差均设为0.1 m,误差矢量绝对值为0.17 m.观测量的噪声均值设置为0,方差设置为1 ps.分时共视判决门限Thod设置为0.03.

利用上述方法进行分时共视时间比对,西安和长春的时间比对判决因子如图8(a)所示,时间比对误差如图8(b)所示,两图均为三维坐标图,X和Y轴分别为西安和长春一天内的秒累计数,两图Z轴分别为判决因子flag和分时共视时间比对误差.从图8(a)可以看出,满足(16)式判决条件的判决因子在西安和长春两地并不是同时发生的,所以两地用于时间比对的解算钟差也不是基于同时刻获取的观测量得来的.从图8(b)可见,两地分时共视时间比对的绝对误差小于40 ps,符合超高精度时间比对的性能要求.图8(b)的分时共视误差包含有残留的轨道误差、钟差建模误差和观测量噪声等,对比图8(b)和图5可知,分时共视方法即使引入了钟差建模误差,建模误差的数量级也远小于轨道原始误差对共视时间比对的影响.

在分时共视仿真实验时设置了空间站轨道误差和观测量噪声,为了分析各项误差对分时共视时间比对的影响,对图8(b)中的误差进行分解.空间站轨道误差经分时共视抵消后的残差如图9(a)所示,误差范围为[−10,5]ps.空间站轨道误差还会对用于建模的空地钟差解算过程产生影响,从而引入建模误差.为了分析这部分误差,在分时共视计算时,(17)式钟差建模的基础数据采用空地钟差真值,而不是解算值,获取模型一次项系数后再进行后面的分时共视比对,两地的时间比对误差如图9(b)所示.图9(b)所示的误差范围在[−10,10]ps左右,平均误差比图8(b)要小十几皮秒,这十几皮秒的误差主要来源是轨道误差对解算钟差的影响,而钟差建模是基于解算钟差进行的,所以这部分误差是轨道误差导致的建模误差.

图8 西安-长春分时共视时间比对结果 (a)判决因子；(b)时间比对误差Fig.8.Results of Xi’an and Changchun asynchronous common-view time comparison:(a)Flag distribution；(b)time comparison error.

对比图9(a)和图9(b),发现即使采用钟差真值建模,时间比对的误差较轨道误差也大了几个皮秒.经过分析,认为是观测量噪声导致的.观测量噪声一方面直接影响钟差解算,另一方面对双频解算电离层延迟也会产生影响,均值为0方差为1 ps的观测量噪声产生的电离层延迟计算误差在5 ps以内,与该部分误差的数量正好符合.为了验证上述分析的正确性,把观测量的噪声均值和方差均设置为0,重新利用钟差真值建模进行分时共视,时间比对的误差如图9(c)所示.对比图9(a)和图9(c)可知,两幅图的误差分布特性几乎一致,细微的差别是由钟差模型和钟差真值之间的偏差造成.因此,论证了图9(a)和图9(b)之间的差别主要由观测量噪声造成.在空间站发射之后,利用空间站进行高精度共视时间比对时,可以采用载波相位平滑伪距方法、卡尔曼滤波法、最小二乘平滑等多种方法对原始观测数据进行平滑预处理,降低观测量噪声的影响,进一步提高空间站分时共视时间比对的性能.

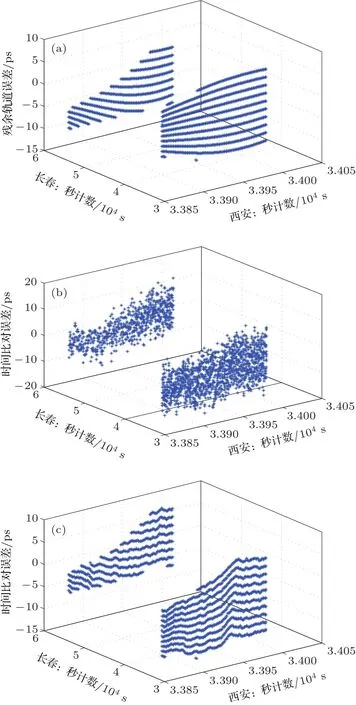
图9 西安-长春分时共视各项误差分布 (a)残余轨道误差；(b)钟差真值建模后的分时共视误差(1 ps观测噪声)；(c)钟差真值建模后的分时共视对误差(0 ps观测噪声)Fig.9.Error distribution of Xi’an and Changchun asynchronous common-view time comparison:(a)Residual orbit error；(b)time comparison error modeled based on the actual clock bias(with 1 ps noise)；(c)time comparison error modeled based on the actual clock bias(with 0 ps noise).

综合上述仿真实验的分析结果可知,利用本文提出的空间站分时共视时间比对新方法,对西安和长春的钟差进行时间比对,比对误差小于40 ps.分时共视的精度主要受空间站轨道误差的残差、地空钟差建模精度和伪码噪声影响.伪码噪声的影响包含直接影响和对电离层延迟解算导致的间接影响.地空钟差的建模精度一方面也受轨道误差的影响,另一方面建模效果还与地面原子钟的特性息息相关.

5.2 西安-喀什分时共视仿真实验分析

从前面空间站的可见性分析可知,西安和喀什不满足传统同时共视时间比对的条件,如果按照传统方法则不能进行共视时间比对.采用本文的分时共视时间比对方法,可以实现西安和喀什的共视时间比对.西安和喀什分时共视的仿真条件和长春基本相同,仅仅喀什原子钟的仿真参数稍有变化,其秒级稳定度为5×10−13,天稳定度为10−14.西安和喀什的分时共视判决因子如图10(a)所示,时间比对误差如图10(b)所示.

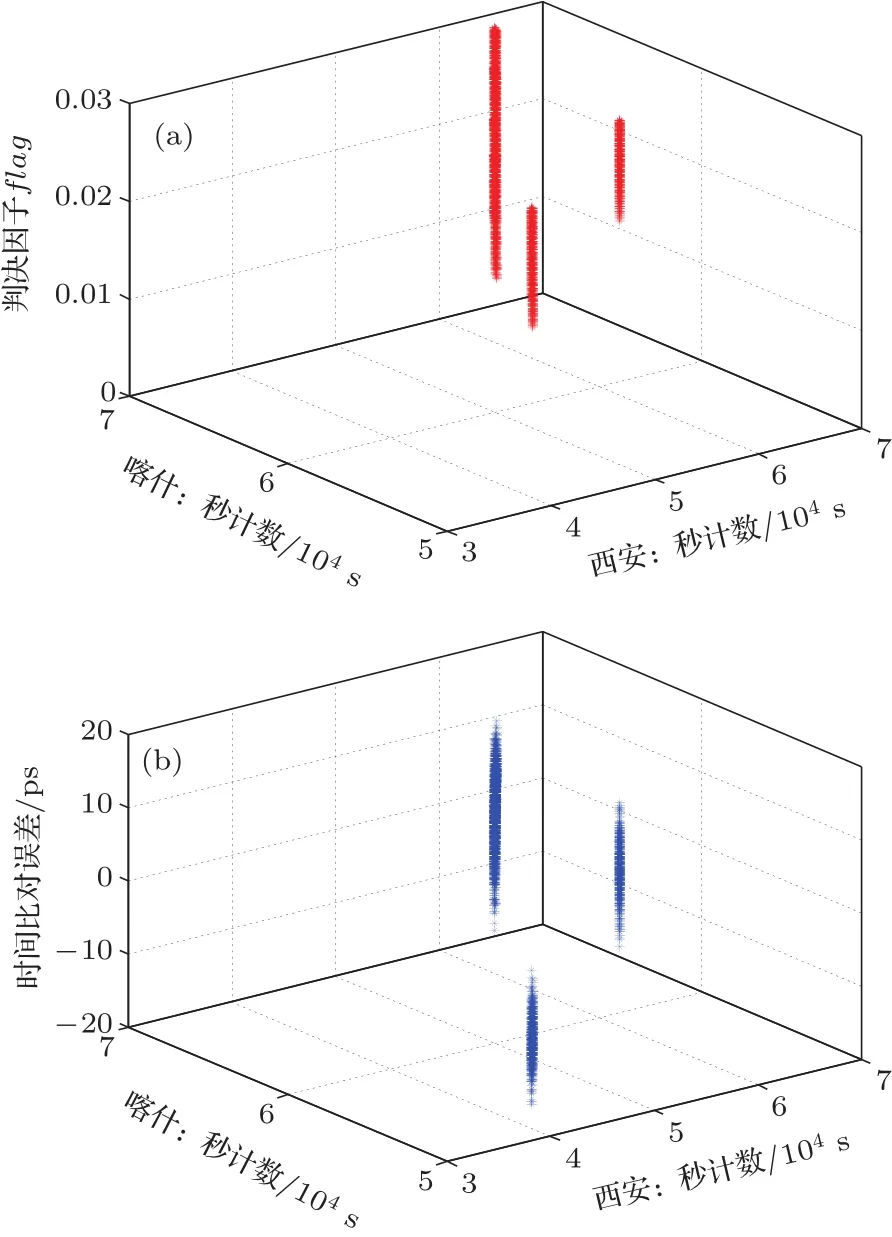
图10 西安-喀什分时共视时间比对结果 (a)判决因子；(b)时间比对误差Fig.10.Results of Xi’an and Kashi asynchronous common-view time comparison:(a)Flag distribution；(b)time comparison error.

从图10(b)可见,西安和喀什分时共视时间比对的误差小于20 ps,既解决了传统共视不能进行西安和喀什时间比对的问题,也实现了超高精度的时间比对.从图10(a)可见,判决门限设置为0.03时,满足条件的西安和喀什分时共视观测时刻并不多.但图10(b)的分时共视时间比对误差较小,小于20 ps.因此,可以适当放大判决门限,以获取更多的分时共视时间比对的样本.

6 结 论

本文以广义相对论理论为基础,分析了进行几十皮秒量级的高精度空间站共视时间比对的工作原理,考虑了皮秒级以上的时延项.基于共视时间比对的原理,分析了传统共视方法的两个应用局限.一方面,传统共视方法对空间站共视时间比对存在一定的应用盲区；另一方面,传统共视方法不能有效地抵消空间站轨道误差,导致时间比对的精度只能达到几百皮秒.本文提出的分时共视时间比对新方法,可以把轨道误差的影响降低至10 ps量级,最终可以实现几十皮秒的共视时间比对精度.此外,本方法不要求两个地面站同时观测空间站,很好地解决了传统共视的盲区问题.通过仿真实验验证了本方法的有效性,能够实现几十皮秒超高精度的时间比对,比对基线可达上千公里,且能很好地应用于传统共视方法的工作盲区.