基于区域CORS的实时精密卫星钟差估计研究
高成发,沈雪峰,,汪登辉,赵 毅
(1.东南大学 交通学院,南京 210096;2.上海华测导航技术有限公司,上海 200233)
1 引言
GPS精密单点定位技术(precise point positioning,PPP)借助国际或区域GPS数据处理中心的高精度实时精密卫星轨道和钟差产品以及互联网、移动通讯服务,完全可以实现实时、单机、厘米级的定位结果[1]。目前,IGS服务组织及其分析中心提供的实时IGS预报产品,其预报轨道(IGU)精度与IGS的最终轨道几乎相当[2]。由于GPS卫星所携带原子钟易受到钟噪声和频移的影响,致使其变化的复杂性难以进行模型化并做出准确预报,因此其对应的预报产品精度较低[3]。目前的IGU预报钟差及其时钟漂移与IGS最终钟差相比,偏差达数十厘米甚至数米,这种精度的钟差产品不能满足一些高精度的应用要求,因此,实现实时的关键是实时精密卫星钟差的估计。
本文探讨了基于区域参考站网络的实时卫星钟差估计方法,提出了基于组合差分模型的精密卫星钟差估计策略,结合重庆的区域CORS数据,实现了算法测试和卫星钟差估计的精度评估,并验证了其实时精密钟差产品对于不同网形区域结构之间的关系。
2 基于区域CORS的精密卫星钟差估计模型
在精密卫星钟差估计和精密单点定位中,国内外主要学者大多采用无电离层组合模型,其非差模型的估计方程如下
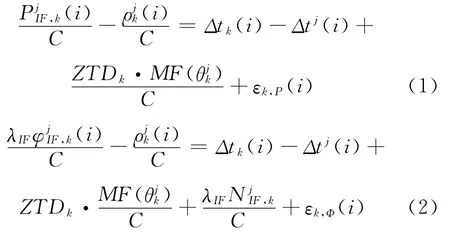
式中,k为测站号,j为卫星号,i为对应的观测历元,PIF、φIF对应无电离层组合的伪距观测值和载波观测值,tk、tj分别代表接收机钟差和卫星钟差,ZTDk为天顶对流层延迟,MF(θjk)为投影函数,θ为卫星高度角,C代表光速,ε为噪声项。
本文利用区域参考站网络,通过星间单差与历元间单差组合差分模型进行实时卫星钟差的估计,具体可分三步进行实时精密钟差的估计。
第一步,构建低采样率星间单差模型;利用CORS网双频原始观测值建立单差无电离层相位观测值组合以及单差无电离层伪距组合,采用经验模型确定观测值权重以及参数初始值,同时采用随机游走过程来模拟对流层参数随机模型,采用白噪声来模拟卫星钟差的变化,利用Kalman滤波并设置一定历元间隔,从而建立绝对卫星钟差滤波器;其单差观测方程为

式中,对于对流层延迟影响,使用全球大气模型GPT设定其大气参数,其干分量部分利用现有经验模型 (Sasstamoinen和Hopfield)可修正至亚毫米级,对于湿延迟部分,由于水汽分布不均匀且变化较快,经验模型对湿分量改正精度较差,约为几个厘米,这里将天顶湿延迟值作为未知参数进行估计。
第二步,建立高采样率相对钟差估计模型。建立历元间差分的无电离层相位观测值组合消除模糊度参数,将卫星钟差历元间变化作为估计参数,同样采用随机游走过程来模拟对流层参数随机模型,采用白噪声来模拟卫星钟差的变化,建立卫星钟差历元间变化估计滤波器,实时估计的历元间的相对卫星钟差,从而建立相对卫星钟差滤波器;观测方程为

通过式 (5)消除模糊度参数,直接采用高精度的对流层延迟模型 (如Niell模型、Saastamoinen模型)估计历元间对流层延迟的变化率,得到简化的误差方程

第三步,对于n个参考站,根据每个参考站估计得到绝对钟差 (基于星间单差的卫星钟差)(i),以及相对钟差 (历元间相对卫星钟差)(i,i+1),分别通过加权平均可得到最终的钟差估计值(i)和(i,i+1)为

式中,pk为权值,由各站钟差计算结果的中误差决定。对于任意时段,得到该时段内1s间隔采样率的相对卫星钟差结果。
在区域CORS的精密钟差估计的数据预处理中,还需考虑相位缠绕改正[4]、相位中心变化[5]、地球固体潮改正、海洋负荷潮汐改正、地球自转改正、相对论效应改正等误差项的影响,以消除系统误差项对钟差结果的影响。
3 基于区域CORS的精密卫星钟差的估计策略
针对本文提出的基于星间单差与历元间差分相结合的卫星钟差估计组合模型,需在构建统一的卫星轨道、初始卫星钟差基准的基础上,选择区域参考站网络的共视参考卫星 (一般以高度角最高卫星),并以此卫星钟作为基准钟。
针对星间单差的绝对卫星钟差估计,建立绝对卫星钟差的卡尔曼滤波器为

由于在卫星钟差估计中,钟差是作为未知参数处理,必须顾及钟差的随机模型。实践表明采用白噪声过程描述钟差随机过程比较简单且有效,即在每个历元,钟差值与其他历元值不相关,钟差参数与其他参数共同解算。
通过建立基于星间单差的绝对卫星钟差滤波器和基于历元间差分的相对卫星钟差滤波器,实时估计得到绝对卫星钟差和相对卫星钟差之后,根据本文提出的方法对绝对卫星钟差和相对卫星钟差进行组合即可得到1Hz的实时精密卫星钟差。而实时卫星钟差一般来说是通过网络播放给用户,但由于时间延迟问题或者是网络中断造成用户无法获得最新的实时卫星钟差,因此用户需要对卫星钟差进行外推,以此获得当前历元的卫星钟差,一般来说若是外推时间不长,广播星历中卫星钟的漂移及漂移速度即可满足外推的要求,即
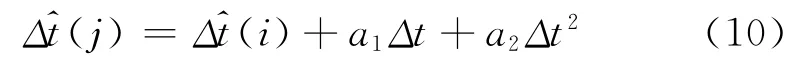
4 实验数据分析与处理
4.1 绝对卫星钟差估计试验
试验网络:重庆市国土资源GNSS网 (CQCORS),包括南川 (NACH)、南岸 (NAAN)等共25个连续运行参考站,该网络中所有参考站均使用天宝天线TRM55971和参考站型接收机,试验时间:2010年11月10日00:00:00~23:59:45(采样率15s)。如图1所示。
试验策略:本文主要从两个方面来试验本文提出的绝对卫星钟差估计策略,一方面比较自编软件解算的钟差与IGS最终发布的钟差产品的一致性;另一方面分析区域参考站网络对于估计钟差的影响因素。
采用二次差比较的方法分析精密卫星钟差估计结果与IGS事后精密钟差的符合程度,即先通过选择某一参考卫星 (可与星间单差形式选择的参考卫星不同),将其它卫星的钟差与参考卫星的钟差作一次差,消除由于基准钟选择不同而对钟差产生的影响;然后,将消除了基准钟影响的计算结果与IGS相应钟差数据之间作二次差,计算实时精密卫星钟差估计的标差值。

图1 采用的CQCORS站分布图
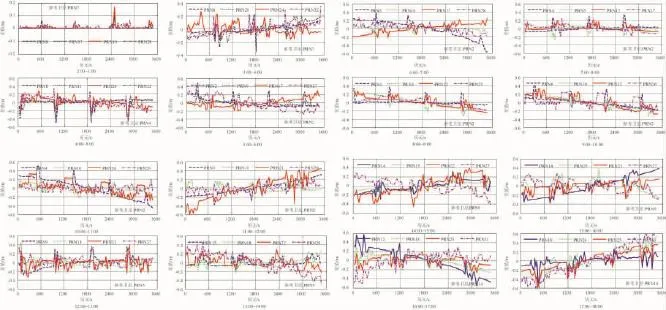
图2 2:00~18:00时间内估计卫星钟差与IGS产品的较差
从图2可以看出,根据本文算法估计得到精密卫星钟差与IGS最终精密卫星钟差间的差值主要在±0.2ns内波动,部分卫星存在一些跳变现象,主要与卫星升降以及相应模糊度重新收敛有关。
从图3可以看出,利用区域参考站网络结合本文提出的绝对卫星钟差估计方法估计得到的卫星钟差与IGS最终精密卫星钟差具有较好的一致性,卫星钟差的估计误差基本都在0.2ns之内波动。此外经统计卫星钟差估计的平均标准差为0.15ns,而IGS提供的事后精密卫星钟差的最终产品精度优于0.1ns,由此可见利用本文提出的基于区域参考站网络的绝对卫星钟差估计方法解算得到实时卫星钟差产品,其精度与国际IGS各分析中心估计的卫星钟差精度基本相当。
4.2 相对卫星钟差估计试验
同样采用上述参考站网络,从两个方面来试验本文提出的相对卫星钟差估计策略,一方面比较估计的相对钟差与IGS最终发布的钟差产品的一致性;另一方面分析估计的相对钟差与绝对钟差的一致性。
统计2:00~22:00相对卫星钟差的RMS值,统计结果见图4。
从图4可以看出,利用基于历元间差分的相对卫星钟差滤波器估计得到的相对钟差与IGS最终精密钟差的历元间差值互差对应的RMS值都优于0.2ns;结合图4也可以看出,在时间序列上也与绝对卫星钟差和IGS最终精密钟差互差的RMS值较为一致,如在时间段7:00~8:00上两种卫星钟差与IGS最终精密钟差互差的标准差都较小,而在时间段17:00~18:00、20:00~21:00上两者的标准差都较大。综合所有时间段可知,平均标准差为0.1ns,其精度与IGS各分析中心估计的卫星钟差精度基本相当。
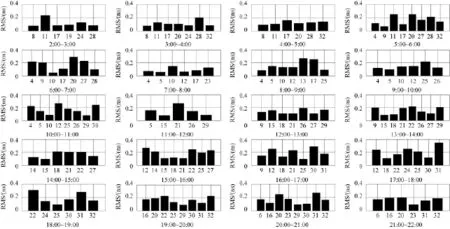
图3 估计的绝对卫星钟差与IGS最终精密钟差作差RMS比较
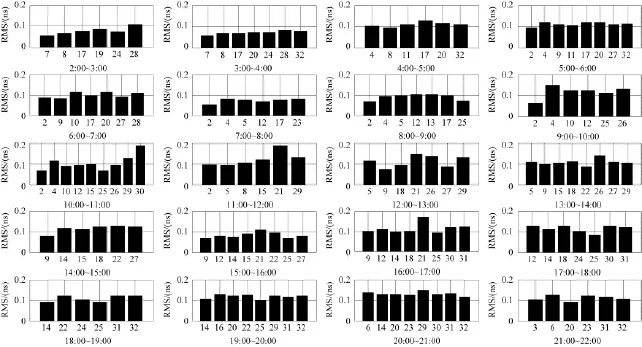
图4 估计的相对卫星钟差与IGS最终精密钟差精度比较
为分析相对钟差与绝对钟差的一致性,将估计得到绝对卫星作历元间差值并与相对钟差进行分析比较。同样根据绝对卫星钟差估计的平均误差值的大小,选择7:00~8:00、2:00~3:00以及17:00~18:00三个时间段,对应的平均标准差分别是0.09ns、0.11ns、0.20ns,比较结果时间序列图见图5。
从图5中可以看出,无论是对于平均标准差较大的时间段还是较小的时间段,估计的相对钟差与绝对卫星钟差历元间差值互差基本都在±2×10-5ns范围内波动,表明估计的相对卫星钟差与绝对卫星钟差历元间差值有着极好的耦合性,两者基本一致,故可以认为相对卫星钟差等同于绝对卫星钟差历元间差值,在实时估计过程,通过估计相对卫星钟差,可以避免绝对卫星钟差估计过程需要估计大量模糊度等相关的参数,简化了实时计算量,而且精度基本不损失,同时也说明通过两者的组合可以较为实 时的准确估计卫星钟差。
4.3 区域参考站网络对估计钟差影响因素分析
利用重庆市国土资源GNSS网,分别选择两种网形的参考站网络分布图,如图6所示的区域A和区域B,进行卫星钟差的估计根据平均标准差值大小分别选择最大(0.20ns)、中等(0.11ns)、最小(0.09ns)3个时间段的解算结果与IGS结果相比较,见图7。
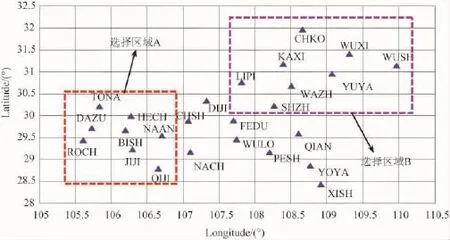
图6 选用的两种网形的CQCORS站分布图
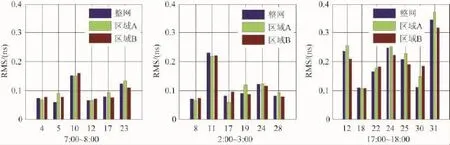
图7 利用不同网形估计卫星钟差与IGS最终精密钟差精度比较
从图7中可以看出,不同区域解算得到的卫星钟差的精度大致相当,而且与整网估计的结果一致;同时也可以看出平均标准差无论是大还是小,其对应时间段解算结果也与参考站网络网形无关。因此可以看出,本文提出的基于区域参考站网络的绝对卫星钟差估计方法具有较好的适应性,与区域参考站网络本身的网形关系不大。
综合上述绝对卫星钟差估计试验与相对卫星钟差估计试验,可以表明利用本文提出的基于星间单差与历元间差分相结合的组合卫星钟差估计模型得到的卫星钟差产品精度基本与IGS各分析中心估计的卫星钟差精度相当,同时也充分考虑的实时性要求,简化了卫星钟差计算的复杂性。
5 结论与建议
本文利用IGU超快轨道与区域CORS观测数据进行实时卫星钟差估计,结合区域参考站网络的特点,提出了基于星间单差与历元间差分相结合的卫星钟差估计组合模型,确定了基于组合模型的实时卫星钟差估计策略,结合卡尔曼滤波参数估计方法,在建立基于星间单差的绝对卫星钟差滤波器和基于历元间差分的相对卫星钟差滤波器的基础上,通过组合实时生成了精密卫星钟差产品。试验结果表明,实时绝对卫星钟差和相对卫星钟差其精度都在0.2ns之内,与国际IGS各分析中心估计的卫星钟差精度基本相当;且估计的相对卫星钟差与绝对卫星钟差历元间差值有着极好的耦合性,简化了计算量,满足了卫星钟差实时性的要求。通过该方法计算的精密卫星钟差产品,不仅可以用于CORS网本区域,还可以用于距离CORS区域达数百公里以外的地区进行实时定位,这对于实时精密单点定位技术的实现具有重要意义。
[1]ZUMBERGE J F,HEFLIN M B,JEFFERSON D C,etal.Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks[J].Journal of Geophysical Research,1997,102(B3):5005-5017.
[2]HAUSCHILD A,MONTENBRUCK O.Kalman-filter-based GPS Clock Estimation for Near Real-time Positioning[J].GPS Solutions,2009,13(3):173-182.
[3]李 黎,匡翠林,朱建军,等.基于IGU预报轨道实时估计精密卫星钟差[J].大地测量与地球动力学,2011,31(2):111-116.
[4]WU J,WU S,HAJJ G,etal.Effects of Antenna Orientation on GPS Carrier Phase[J].Manuscripta Geodaetica,1993,18(2):91-98.
[5]SCHMID R,STEIGENBERGER P,GENDT G,etal.Generation of a Consistent Absolute Phase Center Correction Model for GPS Receiver and Satellite Antennas[J].Journal of geodesy,2007,81(12):781-798.
[6]葛茂荣,刘经南.GPS定位中对流层折射估计研究[J].测绘学报,1996,25(4):285-291.
[7]HAN S.Quality-control Issues Relating to Instantaneous Ambiguity Resolution for Real-time GPS Kinematic Positioning[J].Journal of Geodesy,1997,71(7):351-361.
[8]叶世榕.GPS非差相位精密单点定位理论与实现[D].武汉:武汉大学,2002.
[9]BAR-SEVER Y,BELL B,DORSEY A,etal.Space Applications of the NASA Global Differential GPS System[EB/OL].[2012-12-28].http://trs-new.jpl.nasa.gov/dspace/bitstream/2014/7840/1/03-2193.pdf.
[10]Agrotis L,Dow J,Martinez C G,etal.Real Time GNSS Processing at ESOC:Infrastructure and Initial Results[EB/OL].[2012-12-28].http://www.ngs.noaa.gov/IGSWorkshop2008/docs/RTPoster-agrotis.pdf.
[11]楼益栋,施 闯,周小青,等.GPS精密卫星钟差估计与分析[J].武汉大学学报:信息科学版,2009,34(1):88-91.
[12]李浩军,王解先,王 虎,等.基于GNSS网络的卫星精密钟差估计及结果分析[J].武汉大学学报:信息科学版,2010,35(8):1001-1003.
[13]李星星,徐 运,王 磊.非差导航卫星实时/事后精密钟差估计[J].武汉大学学报:信息科学版,2010,35(6):661-664.
[14]ZHANG Xiao-hong,LI Xing-xing,GUO Fei.Satellite Clock Estimation at 1Hz for Real Time Kinematic Applications[J],GPS Solutions,2011,15(4):315-324.

