部分斜拉桥混凝土脊骨梁受力机理与结构优化

孙建渊， 谢津宝， 涂坤凯

(同济大学 土木工程学院，上海 200092)

部分斜拉桥为介于斜拉桥和连续梁(刚构)之间的一种索辅助梁式结构体系桥型[1-2].部分斜拉桥的先驱是Christian Menn设计的建于1980年的甘特(Ganter)大桥[3].现代部分斜拉桥的结构形式首次由法国工程师Jacgues Mathivat等[4]于1988年提出，其首次明确地提出了Extradosed Prestressed Bridge的概念.而Menn将其1991年在Poya桥上提出的矮塔斜拉桥方案于1998年应用在瑞士阿尔卑斯山区的旅游胜地Kloster镇的Sunniberg桥[5]中，其兼顾了力学与美学，满足了环境景观要求，从而得到采纳.Honigmann等[6]在Menn设计的基础上，进一步详细介绍了概念设计的计算方法以及各关键构件的受力状况与构造确定.部分斜拉桥从出现以来，由于其经济、美观等特点，近十几年来应用日趋广泛，其跨径也在不断增大.

以往部分斜拉桥一般采用单索面布置[2-3]，因为单索面布置让主梁在横向受力上呈现顶板受拉、底板受压的状态，因此在构造布置时只需在桥面板中加入相应横向预应力配筋即可有效解决该问题，因此受力明确，配筋布置相对简单[7].但随着跨径增大及桥面宽度增加，单索面部分斜拉桥主梁抗扭性能不足的问题日益凸显[8].另外，跨径较大时单索面设计往往为减缓抗扭刚度不足，并考虑施工中的稳定，常做成塔墩梁固结体系，使箱梁在荷载作用下出现较不利的剪力滞现象[1].部分斜拉桥采用双索面布置可有效提高主梁的抗扭刚度，一定程度降低单索面所带来的剪力滞效应，且视觉上更为美观[8]，但鲜有展开对双索面部分斜拉桥主梁受力性能和结构优化的研究.而且，双索面布置会使得主梁在横向受力上类似于简支梁，呈现顶板受压而底板受拉的受力特点，成为构造设计上的一个难点.

不同于一般的缆索承重斜拉桥, 部分斜拉桥主梁承载特性一般表现为以承受弯矩为主的梁式桥, 而斜拉索具有体外预应力及辅助索的特征[8].双索面部分斜拉桥索的水平夹角一般不大于30°，主要利用其水平分力对主梁产生预压应力作用，其箱型主梁除支点外无内横梁[8-9]；而斜拉桥是利用其斜拉索的竖向分力支撑主梁，且斜拉索都必须锚固在主梁横梁上，而双索面部分斜拉桥索梁锚固区由于无主梁内横梁，因此其拉索横向传力及受力性能是需要解决的关键技术问题，同时合理的主梁结构及构造形式成为保证索梁横向传力可靠的控制要素[10]，但针对双索面部分斜拉桥的横向受力性能问题，目前国内外尚未有相应构造提出及应用涉及.

以长山大桥——大跨径双塔双索面预应力混凝土部分斜拉桥的概念设计为研究背景，对双索面预应力混凝土部分斜拉桥索梁锚固区的主梁横向受力性能进行研究，并研究基于受力机理及构造优化的具有稳定三角边箱室的预应力混凝土变高度脊骨梁结构形式，以适应斜拉索锚固力的局部作用;采用多向混合预应力布置、边箱室加劲肋构造设计的优化办法，在此基础上采用数值模拟分析建立全桥有限元模型对结构优化的合理性进行验证.

1 工程简介

中国辽宁省长山大桥是世界上第一座预应力变高度混凝土脊骨梁式双索面部分斜拉桥.依据跨海大桥设计通航要求[11]，综合考虑水文、气象、地形地质等条件，确定其主跨为260 m.跨径布置采用双塔三跨式，两边跨140 m对称布置.由于跨径较大，为增强主梁抗扭刚度，斜拉索采用桥面两侧竖直平行双索面布置.为提高结构刚度，减小主梁和塔柱的挠度及变形，采用塔、墩、梁固结体系，同时采用双薄壁墩减小纵向抗推刚度，避免产生过大温度应力[7].考虑到桥位附近机场通航限制，桥面以上塔高确定为37 m.桥梁全宽23 m，其上布置双向四车道，两端各设置1. 5 m宽布索区.为减轻自重及满足主梁承受较大支点负弯矩及剪力的要求采用变截面，变截面梁段长度为57 m，自0号块端部开始到有索区附近结束，并结合内力分析确定主梁支点梁高为9.0 m、跨中梁高为4.5 m.混凝土脊骨梁双索面部分斜拉桥立面布置如图1所示.

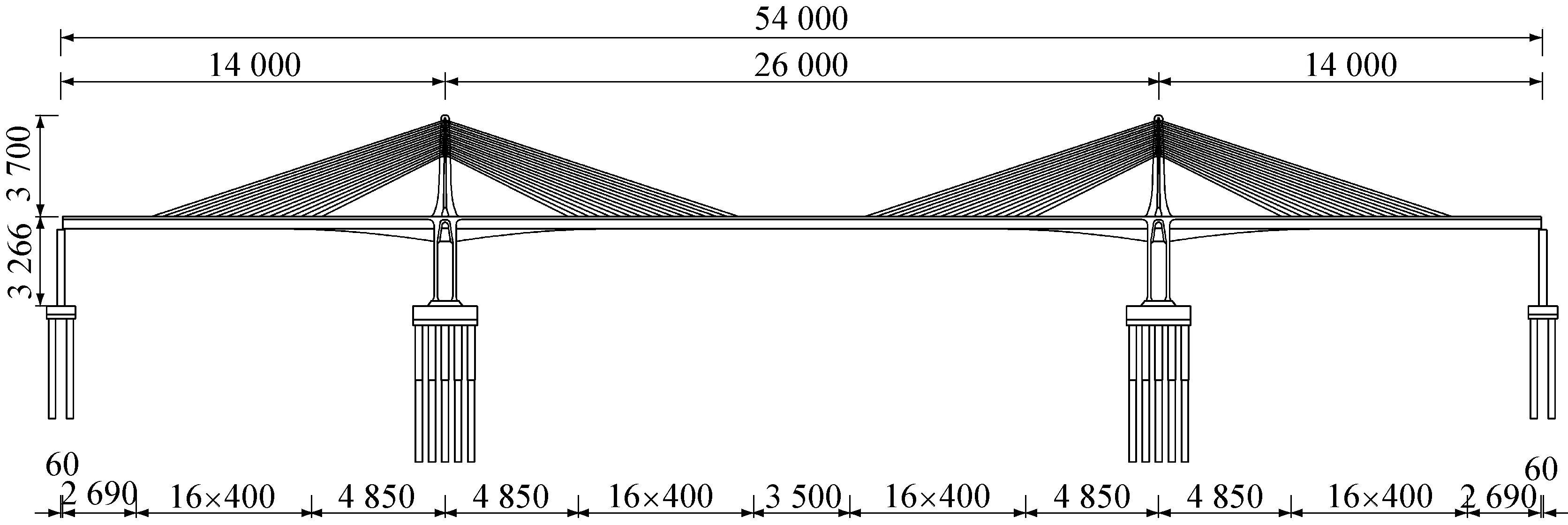
图1 主桥立面布置(单位：cm)

2 部分斜拉桥脊骨梁受力机理

双索面部分斜拉桥的受力类似有体外预应力索的连续梁桥[12]，且采用节段悬臂浇筑施工，故主梁纵向一般采用变截面布置，自0号块端部开始到有索区附近结束[10].同时，为满足双索面布置的受力要求，减小悬臂施工难度、加快施工进度，双索面部分斜拉桥变截面区域仅限于四边形中箱室，其梁高、底板及直腹板厚度沿纵向按二次抛物线变化，脊骨梁两三角边箱室沿纵向尺寸不变，形成如同人体“脊骨”状的构造,如图2所示.

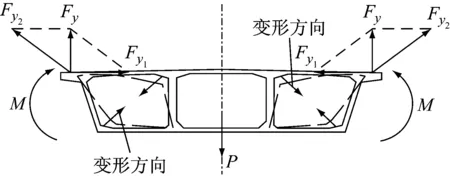
部分斜拉桥索面布置对主梁横向受力有影响，索布置在中间，主梁横向处于悬臂受力状态，索布置在两侧，主梁横向处于简支受力状态，因此索面的布置情况决定了脊骨梁的受力特征、结构构造.在有索区，双索面布置的斜拉索锚固在箱型主梁横向两侧，为箱梁提供弹性支承，在箱梁的两侧产生较大的锚固力，产生竖向分力Fy及沿桥梁纵向的水平力，箱梁在竖向分力Fy、自重及梁上荷载P的作用下，箱型主梁横向受力类似于简支梁，在箱梁横向受到正弯矩M的作用.其内力呈现框架受力模式，外斜腹板、底板受拉，顶板(除两侧悬臂板外)、直腹板受压.

图2 脊骨梁结构形式

若采用常规的倒梯形单箱三室截面，在索力由边箱室传递至中箱室的过程中，由于边箱室为四边形的可变结构，且斜腹板与顶、底板均较薄，刚度较小，其在拉力分量Fy2作用下会发生较大变形，甚至破坏，如图3a.为保证边箱室在传递索力的过程中不致发生过大变形，在图3a截面的基础上进行构造优化，缩短箱底宽度，增加斜腹板的水平投影长度与桥面板的伸臂长度，形成具有稳定三角边箱室的单箱三室脊骨型箱梁，如图3b.

a 倒梯形单箱三室截面

b 扁平三角边箱脊骨梁

在索塔附近的无索区，主梁纵向受负弯矩作用，需对底板进行加厚.同时，中室高度的增加使得斜腹板仅仅固结于直腹板上.主梁横向受力相当于悬臂梁，当车辆荷载Q作用于边室时，在负弯矩M作用下，斜腹板受压.当来自三角斜腹板的冲剪力传递至中室直腹板上固结点A时，会产生应力集中.竖向冲剪力虽可由竖向预应力抵消，但水平冲剪力导致薄弱的直腹板在水平方向产生较大的变形，甚至沿冲剪力方向劈裂，如图4a.针对上述情况，增大直腹板与底板处梗腋的尺寸，使其竖向边长大于固结点A到底板的距离，这样增大了直腹板的刚度，使斜腹板中压应力由梗腋顺利传递至底板，应力线过渡平缓，避免了应力集中，如图4b.

a 改进前

b 改进后

Fig.4Stressmechanismofspinebeaminnon-stayedcablesegment

3 三角边箱脊骨梁配束及构造优化

大跨径双索面部分斜拉桥的整体结构受力状态是支点产生较大的负弯矩、跨中需要承受正弯矩，双索面使得箱梁顶板在有索区横向受压、下缘底板受拉，故双索面部分斜拉桥三角边箱脊骨梁的配束需要采用多向混合预应力布置，主要包括主梁纵向预应力、体外斜拉索、直腹板竖向预应力与无索区桥面板横向预应力以及主梁下缘底板弓形预应力.由于腹板竖向预应力等属于常规布置，所以重点讨论纵向、横向预应力配束优化.

3.1 纵向体内外混合配束优化

目前部分斜拉桥纵向预应力的配置有采用下弯束的经典配束和取消下弯束的直线式配束.直线式配束没有下弯束对梁体产生的竖向分力，造成抗剪能力不足以及主拉应力过大，后期运营阶段可能出现主梁跨中下挠和腹板斜裂缝等病害，故本桥采用经典配束形式进行纵向预应力的布置.由于跨径较大，需要配置较多的预应力抵消荷载作用下主梁截面产生的拉应力.但箱梁有限的截面尺寸限制了预应力孔道的增加，锚固装置的安放也存在困难.为此，将该区域部分顶板束通过连接器接长，锚固在下一个节段末端，弥补截面尺寸限制造成的预应力不足[13].最终确定的纵向预应力布置形式如图5(以中跨为例，取1/2结构).

图5 主梁纵向预应力束布置

Fig.5Longitudinalprestressedtendonarrangementofmainbeam

部分斜拉桥在结构力学上的受力特性接近于带体外预应力索的连续刚构(梁)，斜拉索通过矮塔上设置的转向块——索鞍对主梁产生竖向支反力和水平压力，承担部分荷载效应(约占30%)，对主梁起到一定的辅助作用[14-15].结合部分斜拉桥的结构特点，采用分丝管式鞍座，通过在索鞍内设置分丝小管使每根钢绞线相互平行，从而改善受力，且防腐防水性能好，换索方便，抗滑移性好.

3.2 横向弓形预应力优化

横向预应力的布置需对无索区和有索区分别考虑.在有索区段，除需布置横向预应力束外，还需考虑额外的配束以满足索力作用下主梁的横向受力要求.在双索面布置下，主梁横向受力相当于简支梁.在索力由边箱室传递至中箱室的过程中，截面受正弯矩作用，箱梁下缘底板和斜腹板受拉，需要配置预应力束抵消产生的拉应力.如果在斜腹板和底板分别张拉预应力束，则由于箱梁高度限制以及底板在三角边室设计下长度受到压缩，钢束的锚固长度十分有限，预应力损失很难控制，需要进行优化改进.

根据以往优化竖向预应力时采用的环向预应力筋布置形式，结合主梁的横向构造，在主梁有索区截面设置了“弓形”预应力束.如图6所示，将通长的预应力束穿过底板和两斜腹板，锚固在梁端的悬臂板处，形成“弯弓”状.该布置方式增加了预应力束的长度，解决了预应力损失严重及张拉操作不便的问题.同时，预应力筋的走向与索力的传递路径一致，提高了索力传递效率.在有索区每个施工梁段，“弓形”预应力束沿纵向间隔0.45 m布置，使预应力横向分布趋于均匀.

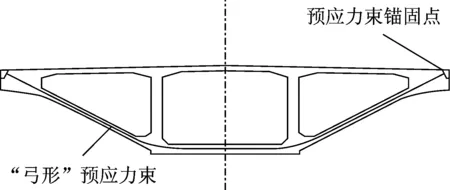
图6 “弓形”预应力束布置

在无索区段，主梁受力与连续刚构桥完全相同.仅需在顶板布置横向预应力束，以加强桥梁的横向联系，增加悬臂板的抗弯能力，并抵抗在车辆荷载和其他荷载作用下顶板下缘产生的拉应力，避免纵向开裂.

3.3 边箱室加劲肋构造优化

箱梁的约束扭转和畸变主要由截面周边变形引起.在当前的工程实践中, 部分斜拉桥往往参照正常斜拉桥, 在索梁锚固处设置横隔板.其优点在于增加截面横向刚度，限制截面约束扭转和畸变，进而减小翘曲正应力.但对于部分斜拉桥是不合理的，因为有索区设置的锚下横隔板不仅会增加主梁结构自重, 还将引起节段施工内模难以拆卸及滑移, 从而造成挂篮难以推进、工期过长等诸多问题.在受力方面，横隔板的存在使得传递至桥面板的有效横向预应力减小.因此，本桥索梁锚固处不设置横隔板，在边箱室设置横向加劲肋限制截面约束扭转和畸变，改善索力传递下截面的传力及受力特性.索梁锚固截面三角边箱室内设置的空三角加劲肋肋高0.5 m、厚0.3 m，其构造如图7.

图7 加劲肋构造(单位：cm)

4 计算分析

4.1 最不利工况验算

根据上述优化后的结构，建立全桥有限元模型并进行整体受力性能的计算，如图8所示.

计算持久状况下的结构应力时，考虑的荷载为自重、二期恒载、预应力以及汽车荷载.此外，为体现材料的长期影响，还需在定义材料性质时引入混凝土的收缩与徐变.全桥关键构件最不利荷载组合应力如表1所示，满足规范要求，其中压应力为负，拉应力为正.而且，主梁中跨在最不利荷载组合作用下的最大挠度仅为10.65 cm，远低于规范限值43.3 cm.

图8 全桥有限元模型

Tab. 1 Most unfavorable load combination stress of key members of full bridgeMPa

4.2 剪力滞效应验算

由于单箱多室部分斜拉桥存在剪力滞效应过大的问题，为了计算双索面布置下主梁采用脊骨梁并进行结构优化后对剪力滞效应的降低程度，首先将全桥划分成有索区与无索区两部分，并以中跨作为研究对象，建立中跨这一典型区域的有限元节段模型，并包含了无索与有索段两部分.由弹性力学中的圣维南原理，结构在远离集中荷载作用点一定距离时其应力状况才会趋于均匀，故建立了较长的有索区段.边界条件采用在主梁一端固结约束、在另一端施加全桥模型内力的方法进行模拟.计算荷载主要考虑运营时的状况，并将全桥模型计算得到的内力结果施加在主梁断面上，故荷载组合为自重、预应力、二期恒载、汽车荷载，纵向布载方式使得主梁跨中应力最大.剪力滞效应分析时活载沿横向对称布置，使得箱梁截面不出现扭转变形，以便研究纵向弯曲变形引起的剪力滞效应.

对有索区分析时,选取在距离固结端有一定距离的主跨四分点处进行，并且考虑加劲肋对于纵向正应力横桥向分布的影响.在前述荷载组合下，有索区关键截面处的顶板纵向正应力分布如图9所示，其中压应力为负，拉应力为正.

由图9可知，顶板纵向正应力全为压应力，沿横桥向分布较为均匀，绝对值最大为12.8 MPa，最大纵向正应力与最小正应力相差均仅在0.5 MPa左右.直腹板处顶板纵向正应力略小于边、中箱室中心处顶板纵向正应力，负剪力滞效应不明显.

对无索区的分析需要考虑跨中处钢束锚固和全桥模型内力的影响，故选取主跨中间处分析.在前述荷载组合下，有索区关键截面处的顶板纵向正应力分布如图10所示，其中压应力为负，拉应力为正.

图9 有索区顶板纵向正应力在横向的分布

Fig.9Transversaldistributionoflongitudinalnormalstressofthetopplateinstayedcablesegment

图10 无索区顶板纵向正应力在横向的分布

Fig.10Transversaldistributionoflongitudinalnormalstressofthetopplateinnon-stayedcablesegment

如图10所示，关键截面顶板纵向正应力全为压应力，最大绝对值出现在直腹板处顶板，为5.5 MPa，但该截面处正剪力滞效应并不明显，与中箱室中部应力相差不大.在边箱室处，纵向压应力由直腹板处向边箱室边缘处递减，在边箱室斜腹板处存在最小压应力4.0 MPa，表现为一定负剪力滞效应.

截面最大剪力滞系数λe可表示为

(1)

假定实际的顶板纵向应力σx沿厚度方向没有变化，令

(2)

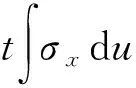
对式(2)进行变换后，可得有效宽度比为

(3)

基于前述公式，可求得最大剪力滞系数λe与有效宽度比B，如表2所示.

表2有索区、无索区最大剪力滞系数与有效宽度比

Tab.2Maximumshearlagcoefficientandeffectivewidthratioinstayedcablesegmentandnon-stayedcablesegment

位置σmax/MPaσe,x/MPaλeB有索区12.8011.201.140.97无索区5.455.441.000.90

由表2可知，剪力滞效应得到很大程度的降低，证明了双索面部分斜拉桥主梁采用脊骨梁结构形式的合理性.

4.3 加劲肋对横向受力的影响

为了确定加劲肋的设置对横向受力的影响，可建立设置横隔板、设置加劲肋和不设置横隔板3种不同的有限元节段模型进行比较分析.

混凝土主梁采用实体单元模拟，并在有索区段模拟主梁锯齿型锚块及锚垫板.在设置加劲肋模型中，加劲肋肋高50 cm、厚度30 cm，加劲肋与顶、底板间设置20 cm×20 cm的直倒角，加劲肋中心在顺桥向位于距离锚固中心0.775 m处；在设置横隔板的模型中，横隔板厚度30 cm，设置在顺桥向距离锚固中心0.775 m处.预应力钢束采用杆单元模拟，按设计要求考虑纵向、横向、竖向预应力，并考虑由于摩阻力、预应力松弛和锚具变形造成的损失，通过设置初应变模拟预应力效应.边界条件采用一端固结、一端对称约束的方式，在靠近桥塔侧的一方固结所有节点，在跨中处对所有节点均采用对称约束，结构模型如图11所示.

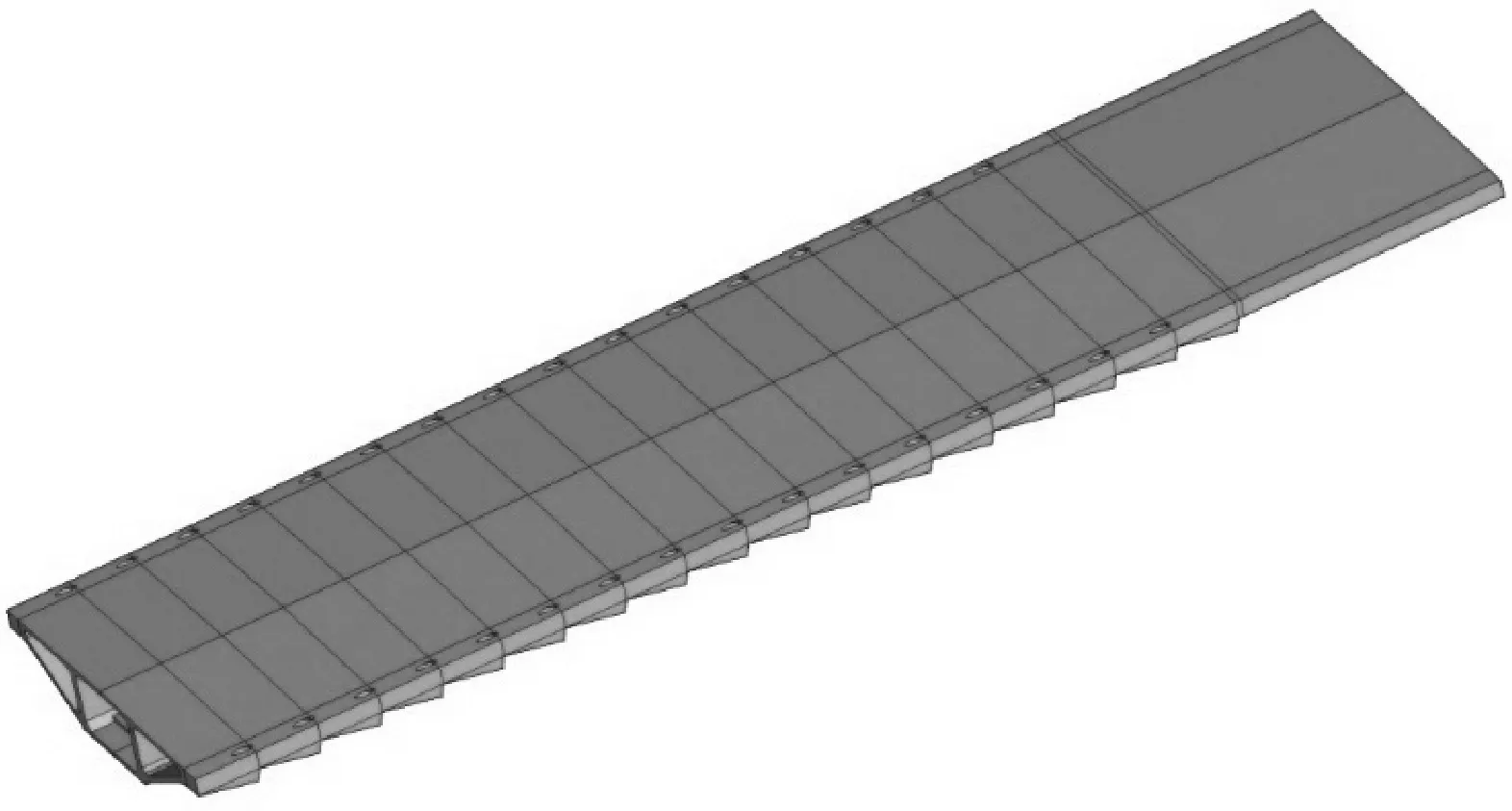
图11 中跨节段模型

在模型加载中，将最大偏载下的汽车活载分解为对称荷载和非对称荷载，分别计算出对应的正应力数值.在表3中，列出了3种构造下反对称荷载(σa)作用下顶板最大翘曲应力以及对称荷载和恒载(σp+σs)(包括自重、预应力和拉索索力)作用下顶板最大弯曲应力.

表3不同构造下顶板最大正应力

Tab.3Maximumnormalstressofthetopplateunderdifferentstructures

情形σa/MPaσp+σs/MPaσaσp+σs横隔板0.0313.620.9%加劲肋0.0312.821.1%无横隔板0.0342.371.4%

由表3可知，3种情况下的翘曲应力均远小于对称荷载和恒载作用下的弯曲正应力.故设计时可忽略翘曲应力的影响，无需采取构造措施.

双索面部分斜拉桥索力主要通过三角边箱室传递到全桥，为了明确以上3种构造对于索力传递的影响，在只考虑索力作用下，计算主梁的横向应力分布.其中顶板下缘和底板上缘受力较为不利，其应力分布如图12、图13所示.

图12 顶板下缘横向应力

图13 底板上缘横向应力

从图12、图13可知，在不设横隔板时，边箱处顶板最大压应力为4.82 MPa，底板最大拉应力为2.94 MPa.设置横隔板和加劲肋时，边箱处顶板最大压应力分别为2.87 MPa和3.13 MPa，底板最大拉应力分别为1.41 MPa和1.49 MPa.可见设置横隔板和加劲肋均可以减小边箱处最大压应力和拉应力数值，使应力分布更均匀，有利于索力横向传递.但两者应力相差不大，对索力横向传递影响相近.

基于上述分析，在限制箱梁畸变、改善索力传递方面，在边箱室设置加劲肋的作用与横隔板相当，并且方便施工，缩短了工期，是更为经济、合理的设计.

5 结论

(1) 为保证部分斜拉桥双索面布置的箱型主梁传力可靠，首次采用具有稳定三角边室的预应力混凝土脊骨梁，以适应双索面斜拉索在无内横隔梁时锚固力的局部作用，并在无索区通过增大直腹板与底板处梗腋的尺寸，提高直腹板的刚度，使应力线过渡平缓，避免了应力集中，可供工程设计及分析参考.

(2) 为进一步优化主梁整体受力及局部传力，提出了多向混合预应力尤其是“弓形”预应力束的布置方案，以提高预应力传递的有效性；并优化分析确定了在有索区主梁三角边室内设置加劲肋以替代整体横隔板的横向传力构造，使顶底板上下缘应力分布均匀，同时有利于节段悬臂浇筑施工, 更为经济合理.

(3) 采用变高度带三角边箱室脊骨梁构造截面，可有效改善双索面部分斜拉桥的索力传递及截面应力状态的合理分布.数值分析计算结果表明，在最不利状态下全桥应力、挠度远低于规范限值，剪力滞现象得到明显改善，横向受力更为均匀、合理.