球状飞射物对屋面瓦片冲击效应的数值模拟
王 枫, 胡 丰, 黄 鹏, 顾 明
(同济大学 土木工程防灾国家重点实验室,上海 200092)
近年来建筑主体及其围护结构的抗风研究受到普遍关注.当建筑结构设计需考虑围护结构的易损性问题时,风致飞射物造成的破坏就成为一个至关重要的因素.风致飞射物是指在极端风气候条件下(如台风)被吹起的高速飞行的物体[1],而我国是世界上热带气旋登陆最多、受其影响最严重的国家之一[2].风致飞射物对高层建筑立面及低矮房屋屋面造成的冲击破坏作用[3],是台风给登陆地区带来巨大损失的主要原因之一.
目前,国内外学者对冲击效应的研究多集中于建筑玻璃、压型钢板及复合板的数值模拟和冲击试验[4-6],风致飞掷物对低矮建筑屋面瓦片的冲击破坏未得到关注.此外,在已有风致飞射物损伤预测的统计模型中,大多数是针对“区域”尺度(如城市)进行评估[7],很少有研究关注“单体”尺度(如房屋)的损伤评估.而多数风灾破坏往往发生于低矮房屋,对低矮房屋单体风灾破坏的评估与预防是亟待解决的问题.为有效预防风致飞射物引发的次生灾害,有必要对其造成的冲击破坏机理进行深入研究.
多项调查显示[8-9],风致飞射物对低矮房屋屋面瓦片破坏作用显著.选取一种典型的陶土屋面瓦片,参考落球冲击试验数据[10],基于ANSYS/LS-DYNA平台,深入研究球状飞射物对瓦片的冲击碰撞机理,建立相应损伤评估方程,对瓦片的抗冲击性能做相应分析,并计算陶土瓦片在球状混凝土飞射物冲击下的风速阈值.
1 落球冲击试验
落球冲击试验是测试物体抗冲击性能最直接有效的方法[11].笔者参与文献[10]中对陶土瓦片的落球冲击试验,该试验选取一个质量为0.549 kg的混凝土球块对3组陶土瓦片进行落球冲击试验,瓦片几何尺寸如图1所示.试验中,瓦片放置于平台上,落球的高度有规律地增加,直至瓦片被冲击破坏.试验中获取的平均落球高度反映了该陶土瓦片的破坏强度.由于试验中落球的质量一定,故瓦片的破坏能量与落球的高度成正比.图2为整个试验过程,试验结果如表1所示.

a 瓦片截面

b 瓦片俯视图

a 落球b 试验装置c 黏土瓦片破坏情况
图2落球冲击试验
Fig.2Dropballimpacttest
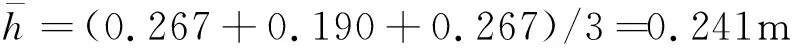
瓦片破坏时裂纹纵向开展,呈现明显的脆性性质.
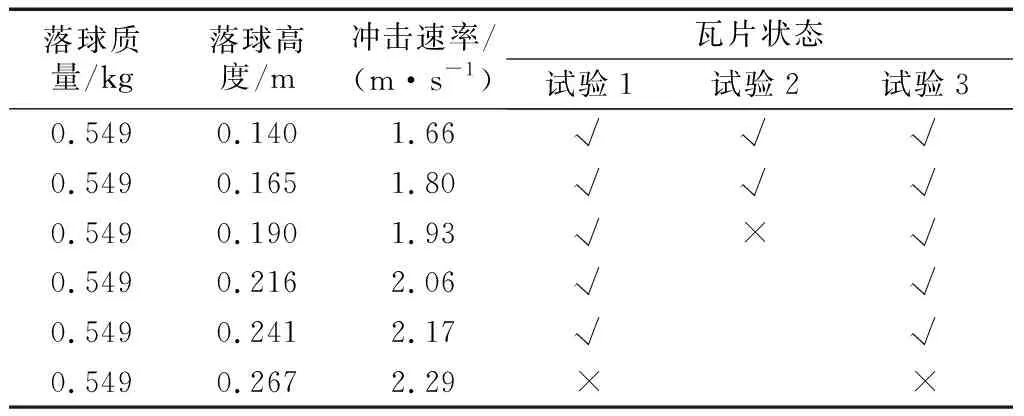
表1 陶土瓦片落球冲击试验结果
注:表中“√”表示瓦片完好,“×”表示瓦片破坏.
2 数值模拟
2.1 数值模型的建立
考虑到碰撞机理的复杂性,为更深入地研究球状飞射物对陶土瓦片的冲击作用,基于ANSYS/LS-DYNA平台,对上述落球冲击试验建立相应的有限元模型.模型中采用3D SOLID164实体单元建立球体及瓦片模型,将球体与瓦片分为2个部分,落球撞击位置为瓦片拱形区域中心,为使计算更加精确,对撞击区域附近瓦片网格进行加密处理,经过网格无关性检验,最终确定计算模型如图3所示.模型共18 032个单元,其中球体单元864个,瓦片单元17 168个.约束瓦片底部的平动自由度即边界条件为简支.

图3 落球冲击试验有限元模型
由于仅关注冲击过程,故设定初始状态为球即将碰撞瓦片的时刻,落球与瓦片的初始距离为0.01 m,定义接触类型为面面接触(surface to surface),接触过程为侵蚀接触(eroding contact).采用Lagrange与单点积分算法并控制沙漏现象[12],计算单位为:cm·g·μs.
2.2 材料模型的选择
数值模型中材料本构模型的选取对于计算结果的准确性有决定性的影响[13].Johnson-Holmquist-Concrete模型能较好模拟混凝土球的特性;由于瓦片在试验中体现出脆性性质,而Johnson-Holmquist-Ceramic模型在模拟脆性材料方面具有独特的优势,故选用该模型模拟瓦片.
混凝土落球模型参数的选取参考文献[14],由于较少研究资料介绍陶土瓦片的材料参数,因此设计试验获取了瓦片的相关材料参数.弹性模量是有限元分析中一个重要的材料参数,其定义如式(1)所示:
(1)
式中:E为弹性模量;σ为试件应力;P为轴向压力;A为试件横截面积;ε为试件轴向应变.
根据美国材料与实验协会(ASTM)E111-04标准进行试验[15],装置如图4a所示,2组试件的横截面尺寸为0.05 m×0.01 m、高为0.08 m.试验数据如图4b所示,取平均值得到陶土瓦片的弹性模量为1.40×1010Pa.总结现有文献[8-11]数据及上述试验数据,确定混凝土落球及陶土瓦片的材料参数如表2所示,表中D1、D2为损伤指数.
2.3 数值计算结果
根据以上材料参数构建的本构模型即可进行相应数值计算,本文计算时长为104 μs,经过反复试算发现,当冲击速率设置为u=2.17 m·s-1时,瓦片仅拱形区域下侧及水平连接处上端部分开裂,并未发生整体完全破坏,开裂情况如图5a所示.

a 试验装置
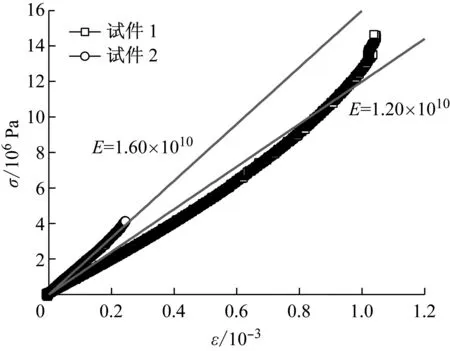
b 试验数据

物体密度/(kg·m-3)弹性模量/GPa泊松比剪切模量/GPaD1D2抗拉强度/GPa混凝土落球2 440300.214.860.0401.00.004 0陶土瓦片1 380140.21.960.0010.50.002 6
当冲击速率增大至u=2.30 m·s-1时裂纹逐渐开展至边缘直至瓦片完全破坏,破坏情况如图5b所示,瓦片裂纹呈十字对称状,纵向裂纹形状与落球冲击试验结果吻合良好.计算结果表明,数值试验与落球试验中临界冲击破坏速率(2.17 m·s-1)误差为6.0%,这有效证明了数值模型的正确性.

a 瓦片部分开裂b 瓦片完全开裂
图5瓦片损伤破坏情况模拟
Fig.5Tiledamagesimulation
当冲击速率u=2.30 m·s-1时,进一步分析瓦片在碰撞历程中的von mises应力状态如图6所示,落球与瓦片在t=850 μs时开始接触,瓦片应力集中于碰撞点附近区域,随着冲击过程的进行,瓦片应力逐渐开展,t=1 100 μs时瓦片内部出现最大等效应力31.31 MPa,最终在t=1 650 μs时扩散到整体,如图6a所示.t=1 900 μs时瓦片边缘开始开裂,t=6 650 μs时裂纹完全开展至边缘,其内部应力分别如图6b和6c所示.在整个时间历程中,瓦片最大应力出现在13 129号单元,选取其时间历程示于图6d中,由图可知,自落球与瓦片接触时刻开始,该单元内部应力激增,到达峰值后迅速衰减,此时单元已达到破坏条件而失效.
2.4 参数分析
以上计算证明了数值方法的正确性,在此基础上对冲击速率u、球块质量m、瓦片倾角α这几个主要影响参数进行分析,以避免试验操作的复杂性,更方便快捷地得到可靠的结果.
以u=2.30 m·s-1、m=0.549 kg、α=0°为基准工况,假定各变量之间相互独立,以控制变量法分别改变每个变量的取值,计算瓦片在各冲击过程中的最大等效应力.例如在研究冲击速率u时,固定球块质量m=0.549 kg、瓦片倾角α=0°,仅改变冲击速率的取值.具体变量参数选择见表3.

a 应力完全开展时(t=1 650 μs)

b 开始开裂时(t=1 900 μs)

c 完全破坏时(t=6 650 μs)

d 第13 129号单元应力时程
图6u=2.30m·s-1时冲击历程中瓦片应力状态
Fig.6Tilestressstateduringimpactprocessatu=2.30m·s-1
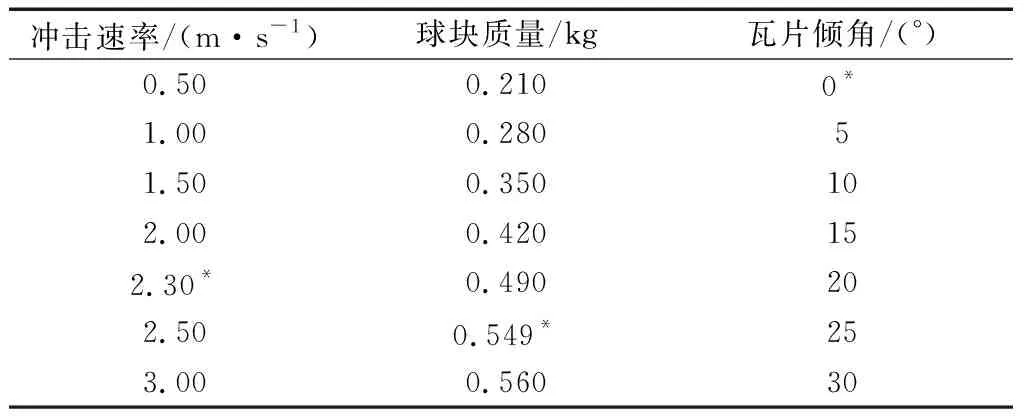
表3 参数分析
注:*为基准工况参数取值.
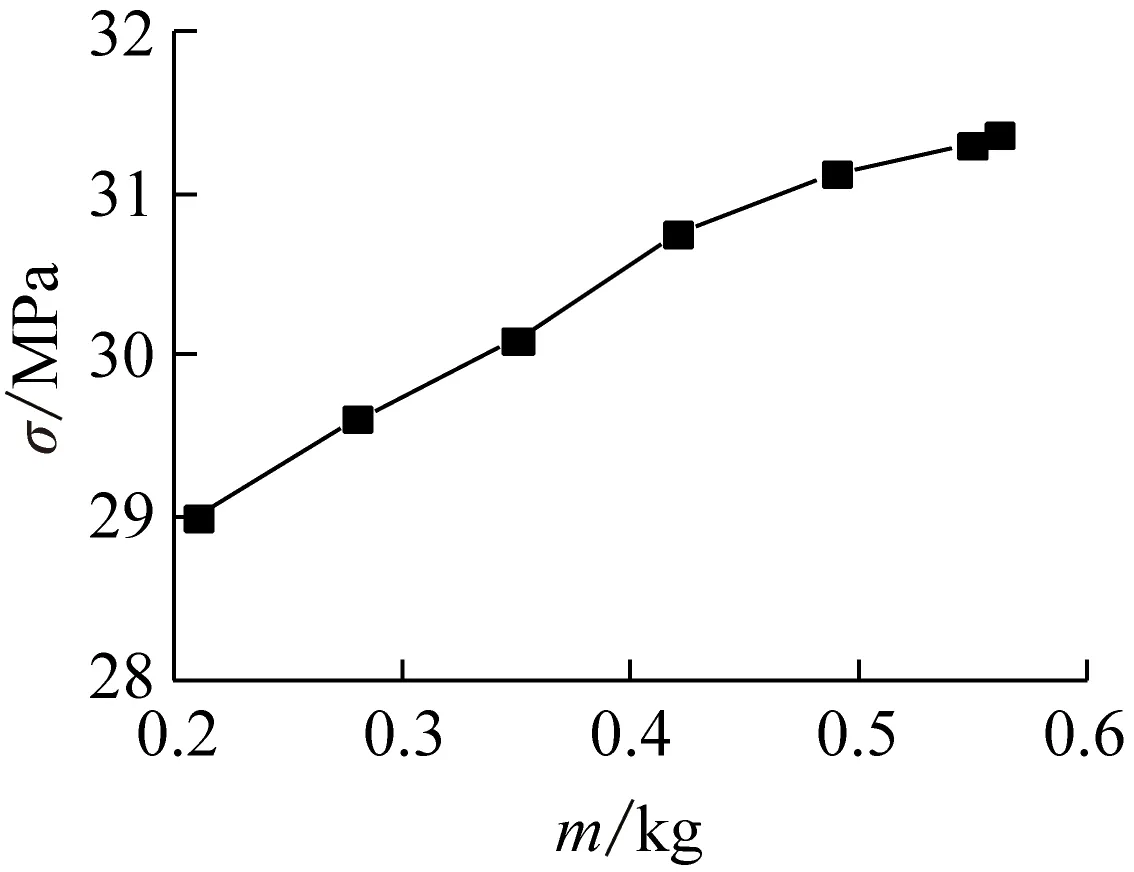
对以上21个参数对应的19个工况(1个基准工况加上其余18组参数对应的18个工况)分别进行计算,提取每种工况下瓦片的最大等效应力,计算结果见图7.由图可知,瓦片最大等效应力与瓦片倾角α相关性不大,与落球质量m和落球速率u近似成正比.当u=3.00 m·s-1时,瓦片最大等效应力为35.77 MPa;当m=0.560 kg时,瓦片最大等效应力为31.38 MPa;当α=0°时,瓦片最大等效应力为31.31 MPa.
3 损伤方程
3.1 飞射物形成条件
在进行损伤估计之前首先应确定建筑周边环境中的碎片是否具备成为飞射物的条件,根据Wills等[16]的研究,物体被风吹起成为飞射物的临界条件为

a 冲击速率
b 球块质量

c 瓦片倾角
(2)

根据上式可得球状混凝土飞射物直径D与来流风速U的关系如图8所示,该图反映了一定风速U下能被吹起的最大飞射物直径D.
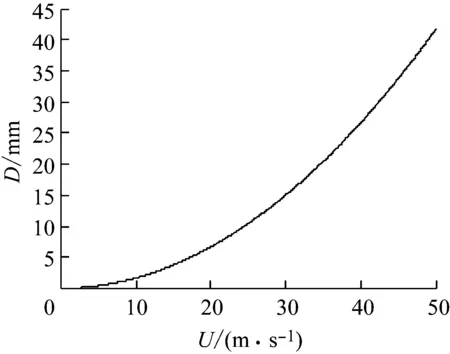
图8 球状混凝土飞射物最大起飞直径与来流风速的关系
以上海地区为例,参考我国建筑结构荷载规范(GB50009—2012)[18],上海地区10年、50年和100年重现期空旷地貌10 m高度处10 min平均基本风压分别为0.40 kN·m-2、0.55 kN·m-2和0.60 kN·m-2,换算成基本风速分别为24.90 m·s-1、29.20 m·s-1和30.50 m·s-1.假设该风速即为来流风速,对应的球状混凝土飞射物的最大起飞直径分别为10 mm、14 mm和16 mm(对应最大起飞质量分别为0.001 3 kg、0.003 5 kg和0.005 2 kg).
3.2 能量损伤方程
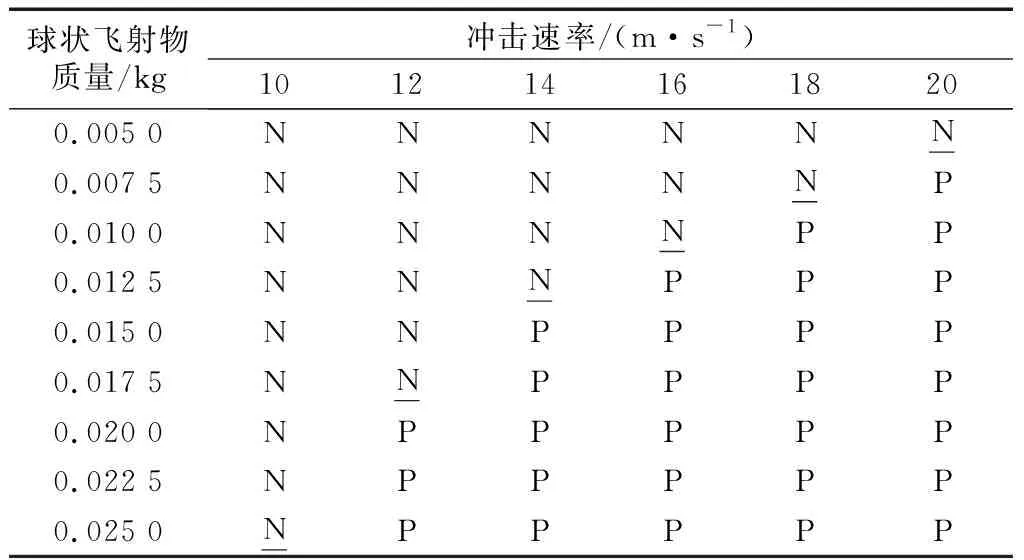
第2节的研究表明,当冲击速率较小、球块质量较大时,瓦片内部最大等效应力与二者均近似成正比,因而多数研究采用落球试验得到的临界动量作为材料抗冲击性能的判别标准.试验所得的临界动量值Rp=m·v=0.549 kg×2.17 m·s-1=1.19 kg·m·s-1.进一步研究表明,当冲击速率较大、球块质量较小时,材料能承受的最大冲击动量较落球试验(相对低速情况)不同.例如选取m=0.070 kg、v=15.00 m·s-1的工况进行计算,其冲击动量为Pdeb=m·v=0.070 kg×15.00 m·s-1=1.05 kg·m·s-1 (3) 式中:Ddeb为损伤指数;K为飞射物速率与来流风速比,根据宋芳芳[9]和Holmes[17]的研究成果,球状飞射物在风速小于40 m·s-1时其最终落地速率约为风速的一半,即K=0.5;RD为临界能量损伤指数. a 不同速率下球状飞射物动能 b 不同质量下球状飞射物动能 Fig.9Kineticenergytimehistoriesofsphericaldebrisduringimpactprocess 由图9a中v=2.30 m·s-1的标准工况计算结果可知,球块的冲击动能为1.45 J,将此动能作为使得瓦片破坏的临界能量值,即取RD= 1.45 J. 将式(2)代入式(3),消去飞射物特征长度,得 (4) 图10给出了能量损伤指数与风速之间的关系,由该图可知能量判别准则下陶土瓦片能承受不超过34.35 m·s-1的来流风速下球状混凝土飞射物的冲击破坏作用,其含义为34.35 m·s-1的风速能吹起最大直径为20 mm的球状混凝土飞射物(图8),这些飞射物造成的最大冲击效应刚好使得陶土瓦片破坏. 由式(4)可知,能量损伤指数与风速的八次方相关,这表明能量损伤指数对风速极为敏感.如图10所示,当风速U增大至35 m·s-1以上时,Ddeb迅速增大,说明风速越大,其破坏程度显著增大. 图10 能量损伤指数与风速的关系 仍以上海地区为例,规范[18]给出上海地区空旷地貌10 m高度处的阵风系数βgz=1.70,则10年、50年和100年的阵风风压(βgzw0,w0为基本风压)分别为0.68 kN·m-2、0.94 kN·m-2和1.02 kN·m-2,换算成阵风风速分别为32.47 m·s-1、38.18 m·s-1和39.77 m·s-1.因此若该陶土瓦片(能承受风速不超过34.35 m·s-1时球状混凝土飞射物的冲击作用)应用于上海地区,在10年重现期的阵风风速下是安全的,而在50年和100年重现期阵风风速下将受到飞射物的冲击破坏. 无论是从动量角度还是从能量角度判别材料的抗冲击性能,冲击物的质量和速度都是至关重要的2个物理量.由这2个物理量可绘制相应的易损性包络曲线. 已有文献表明,台风最大阵风风速常分布在20到40 m·s-1,对应的球状飞射物冲击速率约为10到20 m·s-1.取冲击速率依次为10、12、14、16、18和20 m·s-1.基于第2节的数值模型,取不同质量的球状飞射物反复进行数值模拟试验,记录瓦片的冲击破坏情况.试验结果见表4. 根据上表的临界破坏点即可给出陶土瓦片在风致球状飞射物冲击下的易损性曲线,如图11所示. 由能量损伤方程Ddeb≥RD及瓦片破坏的临界能量值RD=1.45 J推导出瓦片在混凝土飞射物冲击作用下的易损性判别式如下: 表4 陶土瓦片碰撞结果 图11 陶土瓦片的易损性曲线 (5) (6) 将RD代入式(5),给出瓦片在一定风速的飞射物冲击作用下所能承受飞射物的临界质量如式(6),从而可以根据式(6)绘制易损性曲线. 在易损性曲线的左下方区域,瓦片是安全的,即瓦片在球状飞射物的冲击下不会发生破坏.而在易损性曲线的右上方,瓦片将受到飞射物的冲击而发生破坏.将数值模拟结果与能量损失方程判别结果对比可知,数值模拟得到的易损性曲线与能量判别曲线基本一致,数值模拟结果略小于能量判别公式结果,能量损伤方程可作为材料冲击破坏的判别标准.另一方面,2个结果比较一致,也说明了本文数值模拟模型的合理性. 本文数值模拟模型能较好模拟混凝土球块冲击陶土瓦片的冲击破坏过程,数值模拟得到的陶土瓦片的易损性曲线可用于低矮房屋屋面陶土瓦片风灾评估与设计,且其偏于安全. 针对风致飞射物对建筑围护结构的破坏问题,基于数值模拟方法深入研究了球状混凝土飞射物对陶土瓦片的破坏损伤机理,主要结论如下: (1) 球状飞射物-瓦片碰撞数值模型计算结果与落球试验结果吻合良好,数值模型能准确反映冲击过程中应力、应变、位移、能量等关键物理量. (2) 参数分析表明瓦片最大等效应力与冲击速率及球块质量成正比,而与瓦片倾角相关性不大. (3) 冲击过程中球状飞射物的动能呈阶梯式迅速衰减,说明该过程是一个能量显著转移的过程,为能量判别标准提供了依据.在此基础上建立了球状混凝土飞射物对陶土瓦片冲击的能量损伤方程. (4) 该典型陶土瓦片能承受不超过34.35 m·s-1的风速下球状混凝土飞射物的冲击作用.若将该瓦片应用于上海地区,能满足10年重现期下阵风风速所致球状混凝土飞射物的冲击作用,不能满足50年和100年重现期下的设计要求. (5) 在大量数值模拟试验的基础上,并与能量判别方程对比,得到了陶土瓦片的易损性曲线,供设计与评估以参考.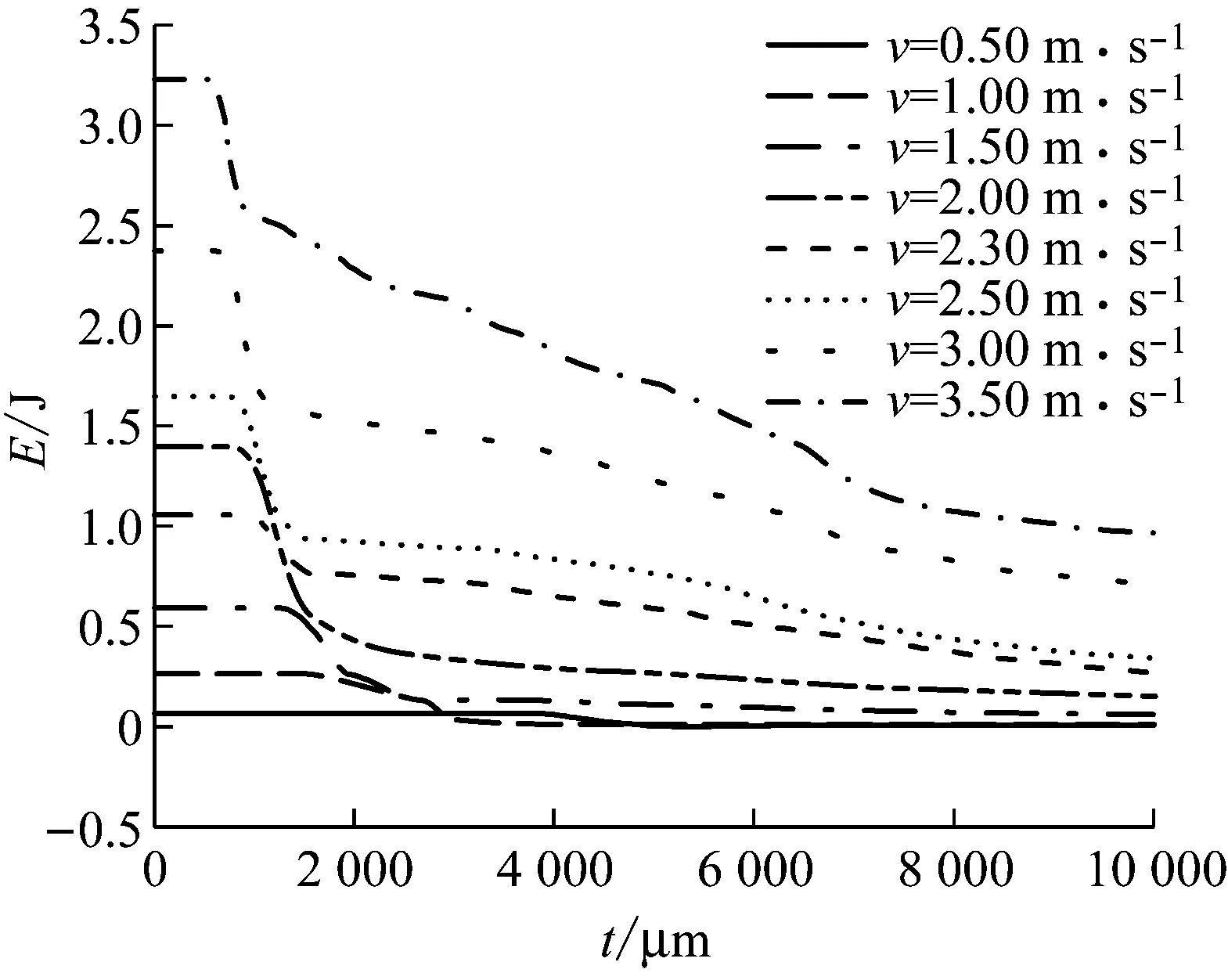


3.3 易损性分析
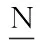

4 结论

