高速列车车内“声-振”特性试验

郭建强， 葛剑敏， 朱雷威

(1. 同济大学 物理科学与工程学院，上海 200092；2. 中车青岛四方机车车辆股份有限公司，山东 青岛 266111)

为满足高速运行工况下的车内压力波动小、乘坐舒适性要求，高速列车为全气密车厢，车体的设计具有良好的水密性和气密性，因此从声音的传播路径上考虑，从车外直接传递到车内的泄露声可以忽略不计.按照激励方式的不同，车外噪声源以空气声和结构声的方式传播到车内[1].从车内声腔的角度考虑，2种方式均体现为内饰板振动与车内声场的耦合特性.笔者曾以高速列车车顶结构为研究对象，分析了车体振动与声场响应的关系，给出了1/3倍频程各频率下的“声-振”关系式[2]，进而针对受电弓区噪声较高的问题，提出一种受电弓减振安装结构，实验室验证降噪效果可达到4 dB(A)[3]，这能够很好地解决了袁旻忞等[4]提出的受电弓区结构声传递问题.文献[5-6]研究了结构振动与声传播的关系，包括声致振动、声波在结构中的传播、不同形式入射波导致的结构响应差异，并对双层板中空结构的隔声性能进行了探讨.左曙光等[7]分析了影响板结构声辐射的主要因素，提出结构振型主导中低频声辐射、振幅决定高频辐射的观点.作者也与帅仁忠等[8]合作，对薄板结构低频隔声性能与振动模态特性进行了研究，并采用声学灵敏度方法研究了高速列车车体型材声学响应与各面板振动的关系，提出了高速列车车体型材断面的声学优化方向[9].

在上述研究基础上，应用振动声辐射理论，在薄板理论假设前提下分析空间声场与板件振动的关系，并用高速列车局部车体台架试验进行验证，用此理论解释高速动车组车内噪声低频峰值来源以及导致隧道运行噪声增加的传播途径2个问题.

1 振动声辐射理论

在均匀的理想流体媒质中，小振幅板辐射声场满足介质的声波动方程[10]，如式(1)：

(1)

声辐射时，结构和声场的协调条件是，垂直于板的声粒子速度分量应等于板表面的法向振动速度.

假设板表面的法向振动速度υn(t)为

υn(t)=υnaejω t

(2)

式中：υna为振幅；ω为角频率；t为时间.

已知板表面任意一点rS的法向振动速度为υna(rS)，通过瑞利积分可得到远场辐射声压[6]：

(3)

式中：ρ0为流体密度；k为波数；S为面积；R=|r-rS|为选取点到矩形板表面一点的距离.

2 局部结构台架试验验证

根据振动声辐射理论可知，空间某点的声压级来源于板上各点振动辐射噪声的叠加.取高速列车车顶局部结构为研究对象，开展台架试验研究与验证.四周采用混凝土墙密封，避免外部其他声源和侧向漏声的影响，顶部为实际的高速列车车顶结构，试验台如图1所示.试验时先用集中力扫频方式激励车体，在车内同时测试内饰顶板振动和距离顶板200 mm处的声压级，建立声压级和振级的关系，如式(4)所示.

Lp=Lv+c

(4)

式中：Lp为声压级，dB；Lv为振级，dB；c为常数.

对于平面声波，声压p与质点速度u的关系如式(5)所示：

p=ρac0u

(5)

式中：ρa是空气密度；c0是空气中的声速.两者乘积是空气的特性阻抗，在20 ℃标准大气压下，ρac0=415 kg·m-2·s-1.

上式两边同时除以p0u0并取对数，可以得到如式(6)所示的声压级和振级关系式：

(6)

式中：p0为参考声压，p0=2×10-5Pa；μ0参考速度，μ0=1×10-6m·s-1.

图1 局部结构试验台

用面声源在车顶施加一个白噪声激励，测试获得各个频段的内饰顶板振动和近场声压级.将振动数据代入式(4)，计算获得的声压级与实测声压级具有很高的吻合度，如图2所示.这说明，内饰板振动和车内声场耦合响应特性在空气声和结构声传播过程中具有普遍适用性，可用于高速列车实车线路运行条件下的车内噪声特性分析.

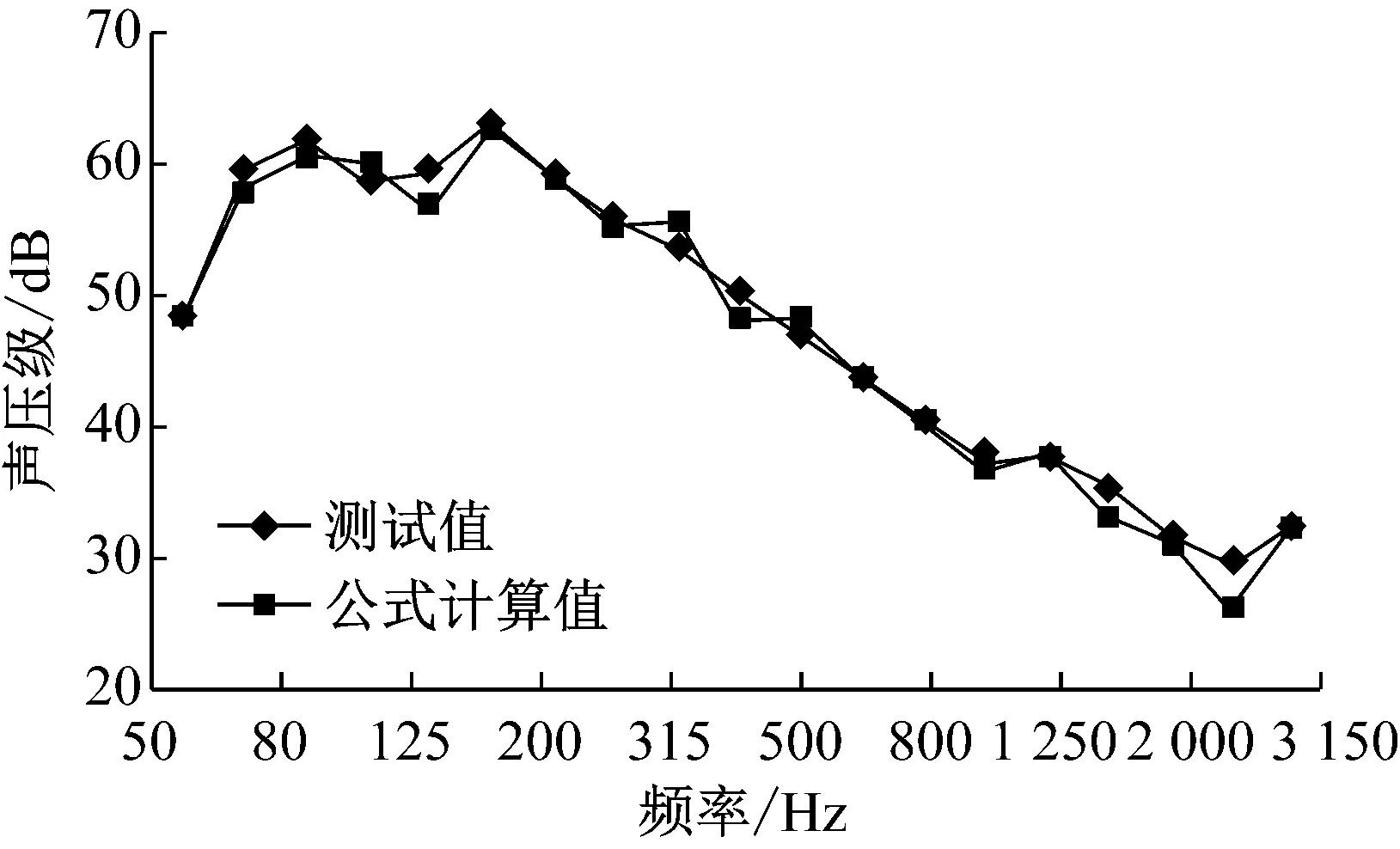
图2 “声-振”关系验证

3 高速列车实车试验

3.1 “声-振”断面测试

为分析车内噪声低频峰值来源，研究导致隧道运行噪声增加的传播途径，在某高速列车线路试验过程中开展了车内“声-振”特性试验，研究不同速度级车内噪声特性与内饰板振动的关系.

列车的内饰板按照结构功能不同，可以分为地板、窗下墙板、窗口墙板、车窗、侧顶板、中顶板六部分.以车辆纵向中心面为分界面，各面板均为左右对称结构，如图3所示.基于这种结构对称性，在进行“声-振”断面测试时，只在半个断面范围内布置噪声和振动测点.测点布置图和现场照片如图4所示.

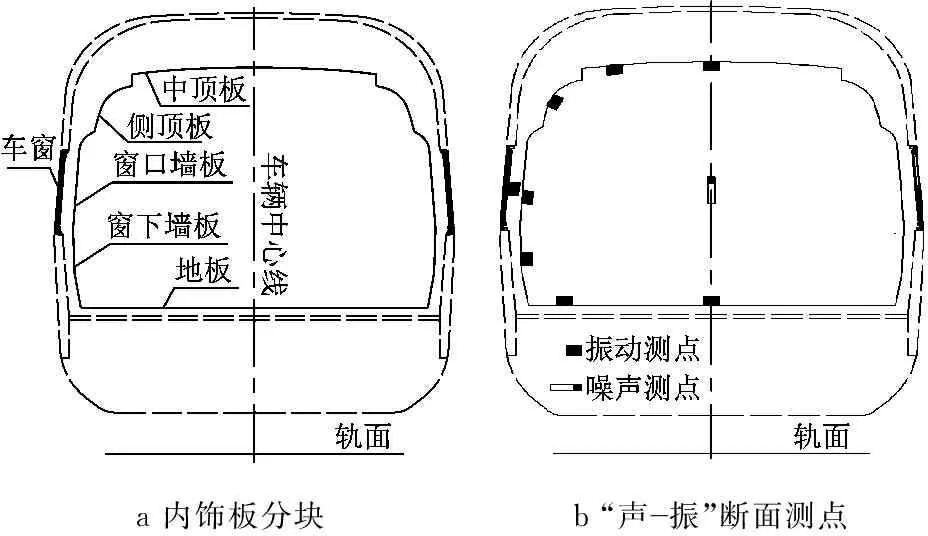
a 内饰板分块b “声振”断面测点

图3 内饰板分块及“声-振”断面测点布置

图4测试现场照片

Fig.4Testsitephotos

3.2 车内噪声和振动的相关性分析

高速列车车内噪声实际上是内饰板振动的响应，车内距离地板面1.2 m的声压级是六部分内饰板振动辐射噪声叠加的结果，可等效为多输入单输出系统.

相干函数γ(f)能够反映输入和输出过程在各频率分量上的线性相关度，可根据输入和输出过程的自功率谱密度函数和互功率谱密度函数计算[11].

(7)

式中：f为频率；Gxy(f)为互相关函数；Gxx(f)和Gyy(f)分别为x、y信号的自相关函数.

相干函数反映了车内噪声与内饰板振动之间的相关性，计算结果表明，绝大多数频段的相关性均在0.9以上，整个频段的平均相关系数达到0.94，如图5所示.车内噪声和内饰板振动的高度相关性说明，内饰板振动辐射是车内噪声的主要来源，从内饰板振动的角度来分析车内噪声问题是一种合理可信的分析方法.

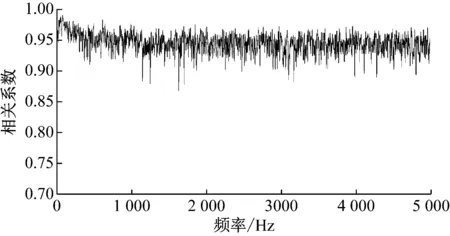
图5 车内噪声与内饰板振动的相关性

3.3 不同速度级的“声-振”特性

图6给出了200 km·h-1、250 km·h-1、300 km·h-1、350 km·h-1四个速度级的车内噪声频谱，并用虚线框出了从噪声峰值下降10 dB(A)的频带范围作为噪声控制的重点频带.可以看出，随着速度级的提升，需要重点控制的频带范围越来越小，越来越向中低频集中，350 km·h-1速度级下的重点控制频带为100 Hz～630 Hz，而315 Hz～630 Hz频带的声压级比160 Hz的峰值低约9 dB(A).若进一步忽略该频带的影响，则高速下车内噪声的重点控制频带为100～315 Hz，这在内饰板振动频谱上的体现尤为明显.以地板振动为例，由于车辆采取的减振措施，总体上看，250 Hz以上的振动幅值较小，个别频率出现振动峰值，在200 km·h-1和250 km·h-1速度工况下，与低频幅值相当，在300 km·h-1和350 km·h-1速度工况下，则远远小于低频峰值，如图7所示.

图6 不同速度级车内噪声频谱

图7 不同速度级下的内饰地板振动频谱

3.4 350 km·h-1速度级“声-振”特性

车内1/3倍频程谱显示，低频成分对车内噪声影响显著，主要峰值频段出现在160～250 Hz频段，其中，160 Hz的峰值最高，如图8所示，比相邻的125 Hz高7 dB(A)，比200 Hz高3 dB(A)，对车内噪声总值贡献最大.分析获得该频段噪声的主要来源，对其进行优先控制，是降低车内噪声最经济有效的途径.

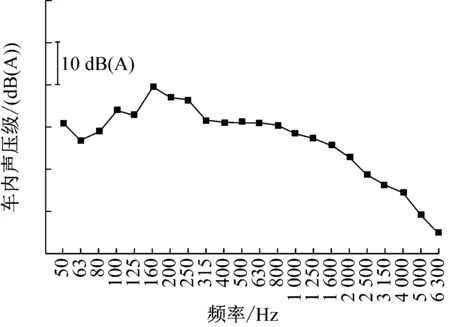
图8 350 km·h-1时车内噪声频谱

对车内噪声进行窄带分析，发现噪声谱上存在148.5 Hz和151.5 Hz两个尖锐峰值，这2个峰值均在160 Hz的1/3倍频带内，是导致该频带噪声高的主要原因.把车内噪声谱分别与地板、车窗、墙板和顶板振动谱进行对比，发现该峰值在地板振动谱上有显著的对应特征，而侧墙结构和车顶结构上无该频率特征，如图9所示.

在140～160 Hz的窄带频段内，对车内噪声和地板振动信号做相关性分析，结果表明148.5 Hz的相关性达到0.92，151.5 Hz的相关性达到0.84，表现出强相关特性，如图10所示.因此，可以确定，160 Hz频带噪声峰值主要来源于内饰地板结构的振动辐射.

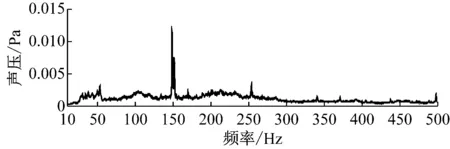
a 车内噪声

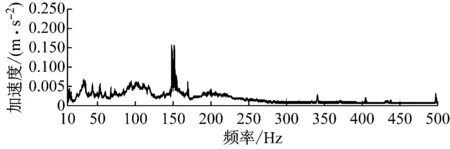
b 地板振动

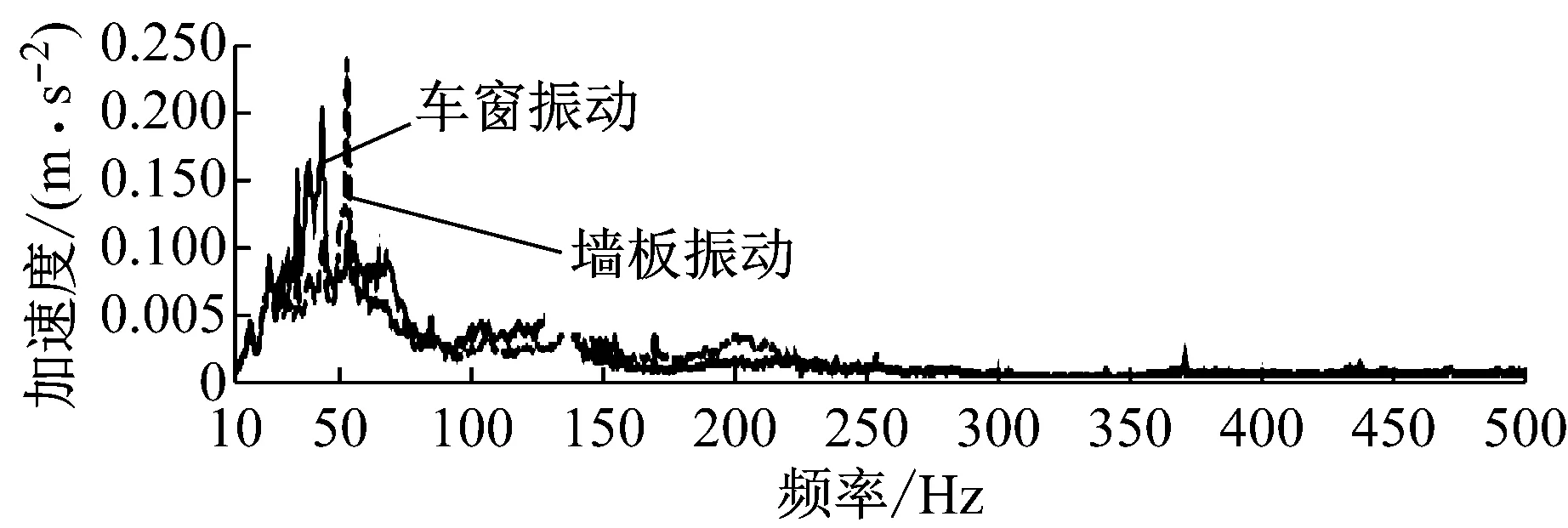
c 车窗和墙板振动

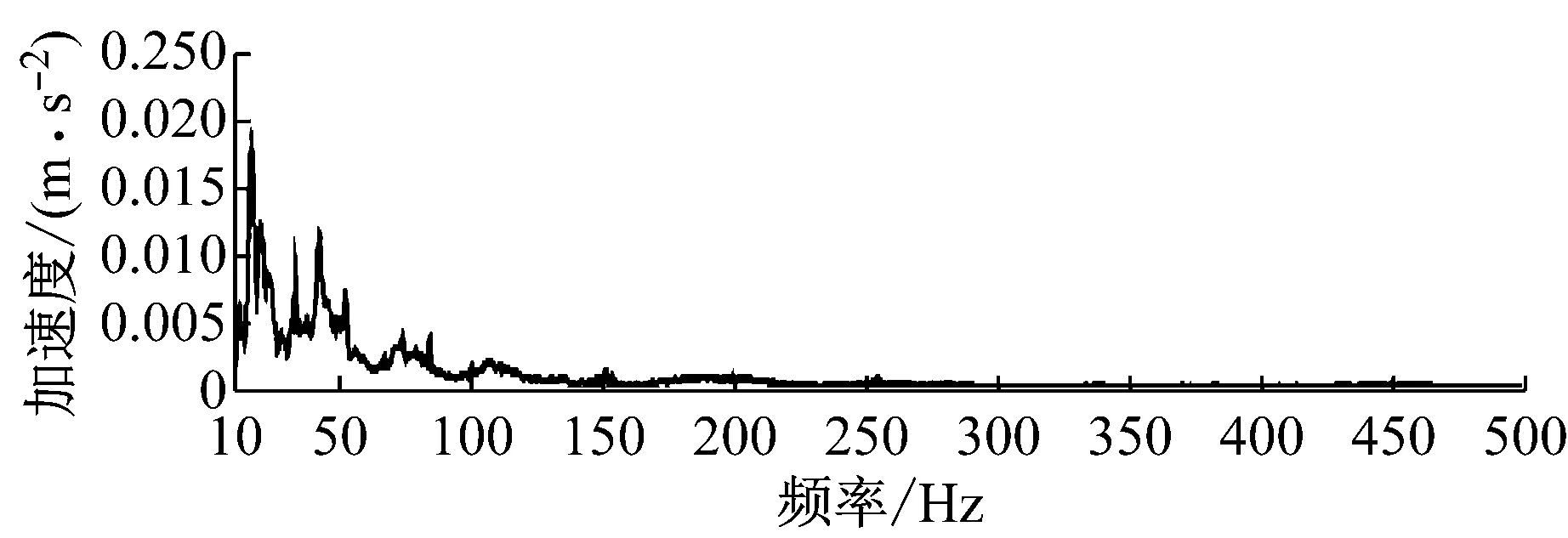
d 顶板振动

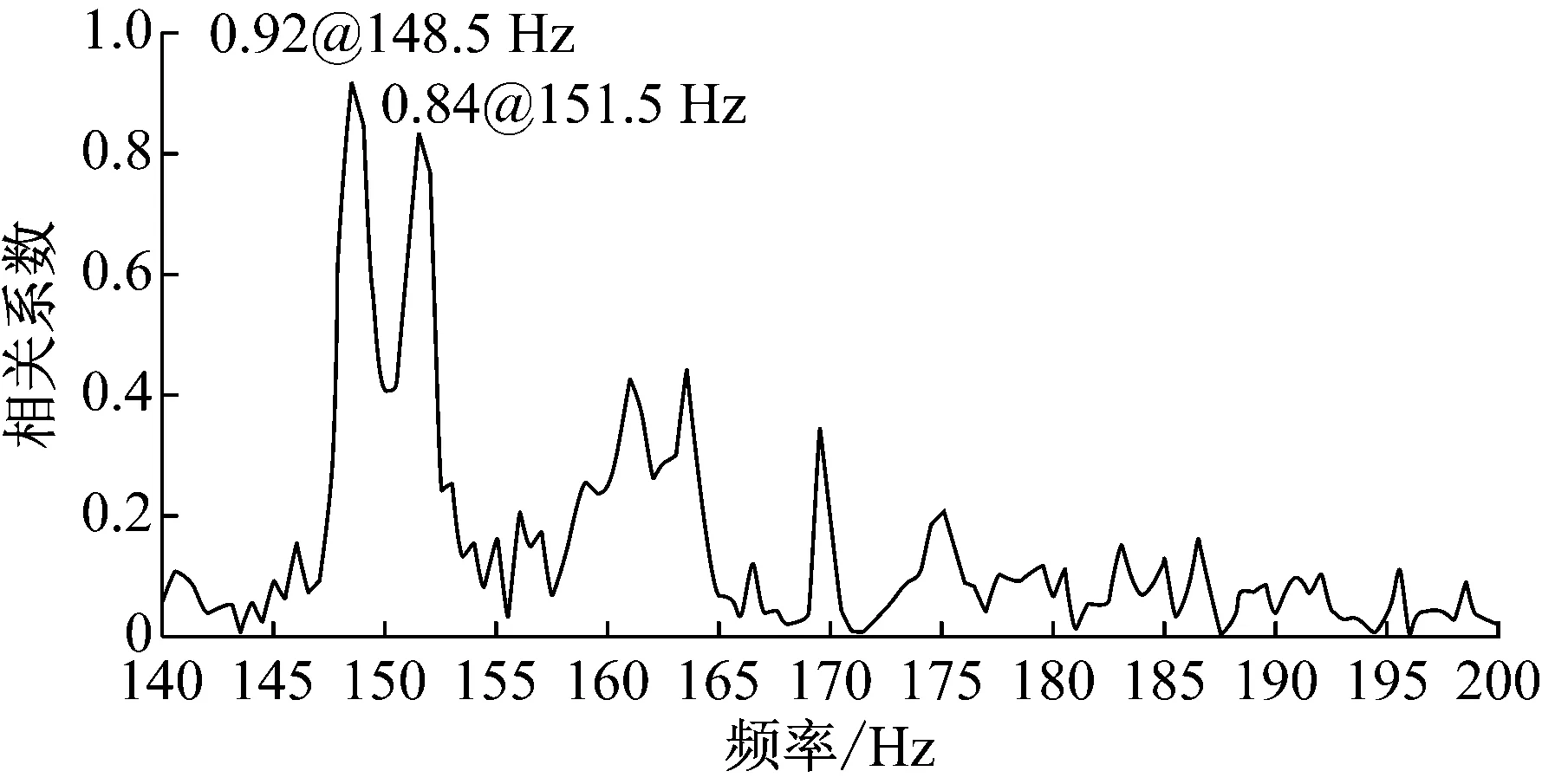
图10 峰值频率噪声与振动的相关性分析

高速列车在隧道环境下车内噪声比明线噪声高8 dB(A)左右，如图11所示，对乘坐舒适性有较大影响.

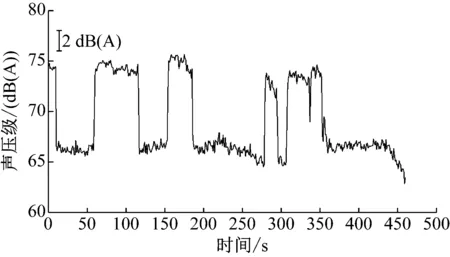
图11 隧道内外噪声差异

采用跟明线工况相同的测点和分析方法对隧道内车内噪声与内饰板振动特性进行分析，结果如图12所示.隧道内外的地板振动幅值和频谱特性基本不变，2个振动幅值依然存在，而墙板和车顶结构的振动大幅增加，增大的频带范围与车内噪声吻合.这说明，隧道环境车内噪声的增加，主要是由于隧道壁面的声反射，更多的噪声能量通过侧墙和车顶结构传进车内导致的.高速列车车下区域原本就是一个相对封闭的狭小空间，而且处于轮轨噪声区域，噪声源较高，因此隧道内的声发射作用对该区域影响较小.由此可见，降低高速列车隧道运行噪声的关键在于加强侧墙和车顶区域的减振降噪措施.

a 车内噪声

b 地板振动

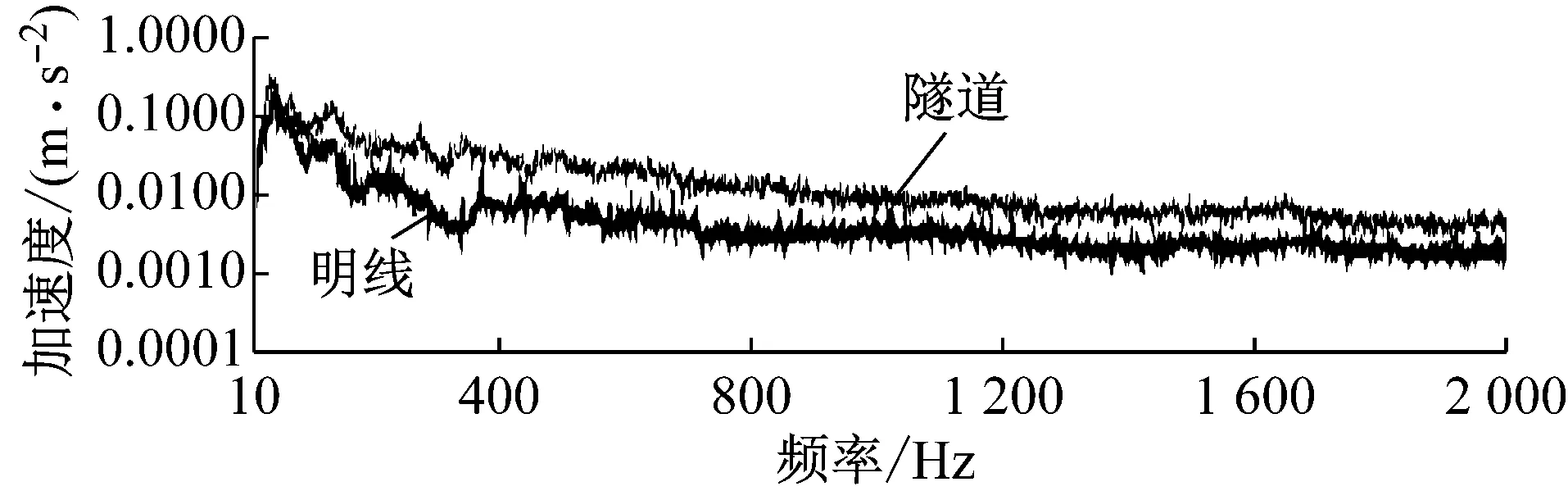
c 车窗振动

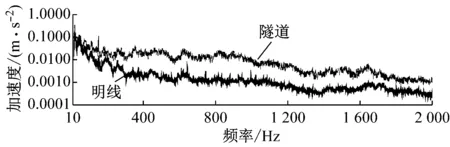
d 顶板振动

Fig.12Narrowbandspectrumofinteriornoiseandvibrationatopenlineandtunnelconditionat350km·h-1

3.5 面板贡献度分析

内饰板分成图3所示的6个区域，在测试获得各区域的振动特性后，可按照式(3)计算获得各面板辐射的声压.由于车内标准点噪声是各面板振动辐射噪声级的总和，按照声能量所占比例，可以计算获得各面板的贡献量，如表1所示.对于明线工况，地板振动辐射的声能量最大，占比达28%，在160 Hz的峰值频率下，达到59%.隧道工况，地板所占比重减小到19%，与此同时，车窗、墙板所占比重大幅增加，贡献最大的是车窗辐射声能量，达26%，而在160 Hz频率下，贡献最大的面板仍然是地板，达39%.

表1 面板辐射噪声贡献量

4 噪声源贡献度分析

前文从车内声场的角度分析了各面板振动对车内空间噪声的贡献量，但内饰面板的振动来源于车外噪声源，采用工况传递路径分析(Operational Transfer Path Analysis，OTPA)方法可以对各噪声源的贡献度进行定量化分析.

4.1 工况传递路径分析理论[12-14]

OTPA是一种利用多工况下实测数据进行传递路径定量化分析的方法.通常在测试过程中选取n(n>1)个激励点，测试m(m≥n)种工况的数据，组成一个m维度的线性方程组，其中第j个工况数据中目标点处产生的响应分别pj(j=1,2,…,m)，第j个测试步中第i个激励处的激励信号为 (i=1,2,…,n)，两者之间的传递函数为hi(i=1,2,…,n)，则有

(8)

其矩阵形式可以简化为

P=XH

(9)

由于选取的测试工况数m大于等于激励源的个数n，可以保证激励源信号矩阵的逆矩阵是唯一的.因此在式(9)两边同时乘以X的逆矩阵，即可得到传递函数矩阵H，如式(10)所示.

H=X-1P

(10)

OTPA方法不需要测试静态下的传递函数矩阵，较传统TPA(Transfer Path Analysis)方法更为方便，并且能很好地对低频噪声贡献量进行预测.因此在轨道车辆噪声传递路径分析中得到广泛应用.

4.2 高速列车噪声源贡献度分析结果

任何一个噪声振动的机械系统都可以用“激励源-传递路径-目标点”的模型来表示.假设高速列车系统为线性时不变系统，则车内目标点的声压等于各个激励源沿着不同的传递路径传播到车内的所有贡献量的叠加.

按照激励方式不同，高速列车转向架区的噪声源可分为声激励和振动激励两大类，如表2所示.

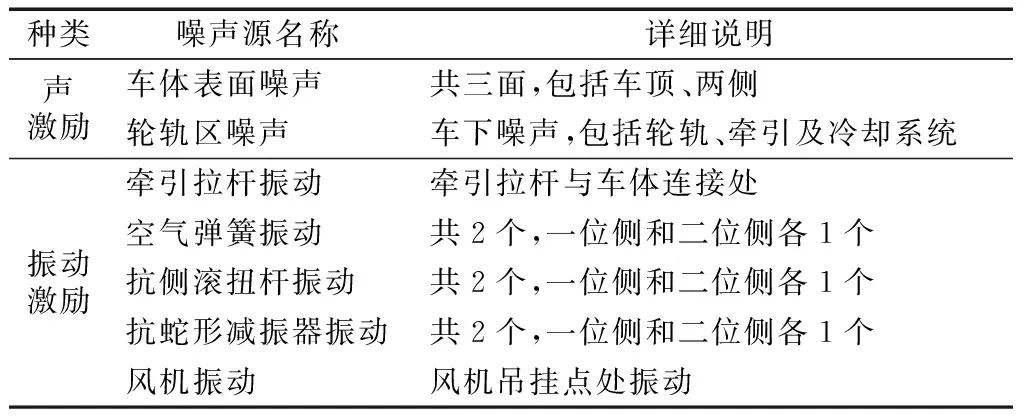
表2 高速列车转向架区噪声源

按照OTPA理论要求，试验时同时测试车内目标点的声压级、车外7个声源处的噪声和振动数据，并测试了多个恒速运行速度级、加减速运行等多个工况的数据，获得了比较理想的传递函数矩阵.对于350 km·h-1速度级工况，采用OTPA方法对各噪声源的贡献度进行分析，结果如图13所示.车体表面噪声对总声压级的贡献最大，达27.0%，而空气弹簧、抗侧滚扭杆等5个振动激励所占比重的总和达到61.0%，对车内噪声的贡献度大于声激励的总和.这是因为高速列车车体结构高频隔声量较大，从而导致车内噪声中低频突出，这是结构声传播的主要频率.在160 Hz峰值频率处，贡献度最大的是风机振动，达27.0%，其次为车体表面气动噪声和牵引拉杆振动激励，因此优化风机安装结构和牵引拉杆节点参数有利于降低该峰值噪声.

图13 噪声源贡献度

5 结论

高速列车明线运行工况的车内噪声以低频噪声为主，在隧道运行环境下，1 000 Hz以下的中频噪声显著增加，分析获得这些噪声成分的主要来源，是开展减振降噪结构设计的前提.利用高速列车高气密性的特点，在不考虑直接透射声的前提下，利用结构振动声辐射理论，计算了某高速列车明线和隧道运行条件下的车内噪声特性及面板贡献度，并用OTPA方法进行了车外噪声源的定量化分析.结果表明，明线工况的低频噪声峰值主要来源于地板结构声辐射，贡献度达28%，而隧道环境下侧墙和车窗等结构的声辐射比重增加.160 Hz的峰值频率则主要来源风机和牵引拉杆振动，并通过地板断面传递到车内.