基于相干分析的复杂船舶系统噪声源识别方法研究
周福昌,吴书有,杜兆伟
(武汉第二船舶设计研究所,武汉430064)
船舶机械系统复杂,系统运行过程中,振动噪声激励源多,试验获得的噪声数据是多激励源综合结果,从测试结果识别和分离各激励源的贡献,对于认识噪声源及其传递特性、制定振动噪声控制措施具有重要意义。在系统噪声源识别技术早期,通常使用分步开启法进行噪声源识别,并被工程界一直沿用至今。该方法简单、直观,是现今船舶机械设备噪声源分离常用的方法,但该方法要求设备能够实现逐一开启,而很多大型设备开启需要很多辅助系统设备开启,分步开启法就不能满足要求。
上世纪70年代,国外基于信号处理技术的噪声源分析得到了蓬勃发展。1971年ROTH P R[1]首先在有背景噪声条件下用常相干函数正确识别了噪声源,但对于相关噪声源识别的问题,相干分析就无法准确识别出噪声源;1975年KOSS L L[2]把多重相干函数和偏相干函数同时应用于冲压机上瞬时噪声源的识别,这是用偏相干函数识别噪声源的成功例子之一;1983年J.S贝达特编制《相干分析和谱分析在工程中的应用》[3]一书,有效推动相干分析在噪声源识别领域研究。国内是自80年代中开始研究偏相干技术的,杨德森利用相干方法识别存在相干性的多激励源[4],宋晶等利用相干函数,进行汽车整车噪声源的识别研究[5],许锐等初步开展相干分析方法在船舶噪声源分离研究[6],但偏相干计算相对繁杂[7],国内运用偏相干方法开展船舶噪声源分析研究工作较少。
本文针对船舶典型系统多台设备开启线谱噪声难以定位的问题,运用相干分析、偏相干分析和重相干分析等分析方法,建立多泵源线谱噪声识别流程和方法,针对船舶系统噪声测试结果,开展其线谱噪声源识别和分离,得到典型系统噪声主要低频线谱来源,为系统主要噪声源控制提供有力支撑。
1 相干分析理论
1.1 相干分析
在单输入单输出系统中,只有一个输入项和一个输出项,相干函数描述输入与输出之间的因果性,相干函数公式如下
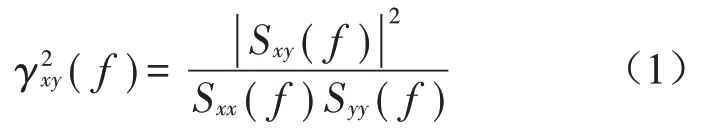
相干函数的谱密度

常相干函数是两个信号的互谱除以2个信号自谱乘积开平方,主要用于单输入单输出系统,它能够有效地识别输入和输出在各频率处的因果关系。
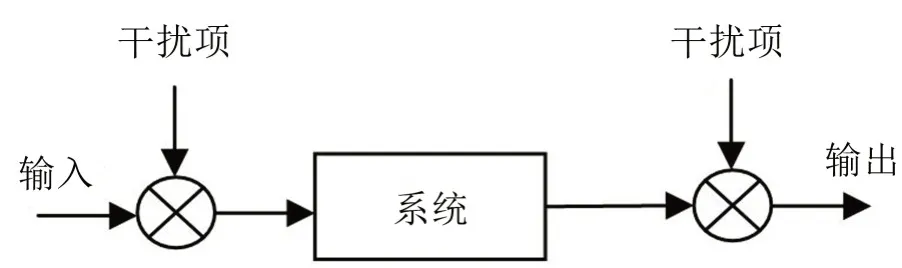
图1 单输入单输出系统模型
当相干函数为1 时,表示输出信号与输入信号完全相干,系统不受干扰而且系统是线性的。当相干函数在0~1之间,则表示有如下3种可能:
1)测试中与外界噪声干扰;
2)输出是多个输入的综合输出;
3)联系输入和输出的系统是非线性的。
对于多输入单输出系统,当各个输入完全不相关时,常相干函数也可用于判断输入与输出之间的因果关系。然而在工程实际中,常见的情况是多个输入信号具备一定相关性,这时常相干函数则不能有效进行因果关系的判断。
1.2 偏相干分析
在多输入单输出系统中,多个噪声源一般都不是各自独立的,而是存在一定的相关性,正是由于这种相关性的存在,常常能减弱甚至掩盖真源与输出之间的关系。偏相干函数就是为了分析多源系统而产生并发展起来的一种谱分析方法。
用一组有序的条件输入记录代替原始的已知输入记录,就可以得到代替图2的另一种模型图3。
按图3所示次序选择的条件输入记录的有限傅里叶变换记为{Xi·(i-1)!} ,i=1,2,…,q。对任何i,项Xi·(i-1)!表示前面X1,X2,…,Xi-1条件下的Xi,也就是用最小二乘法从Xi中去掉X1到Xi-1的线性影响。
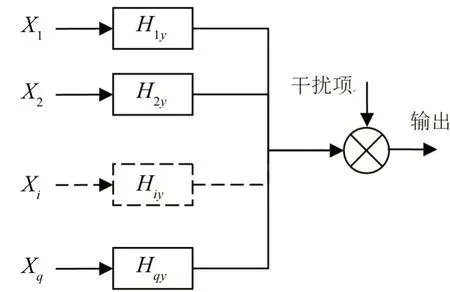
图2 多输入单输出系统模型框图
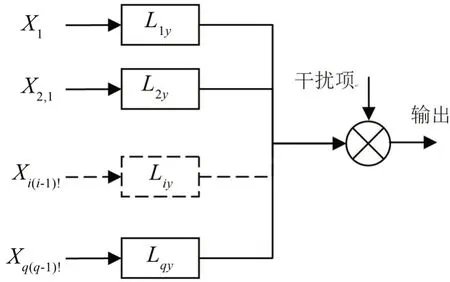
图3 条件输入时的多输入单输出模型
这些有序条件输入记录将是两两不相关的,原始的输入记录一般不满足这个性质。条件功率谱如下
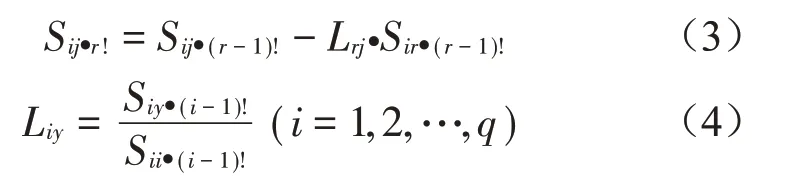
偏相干函数
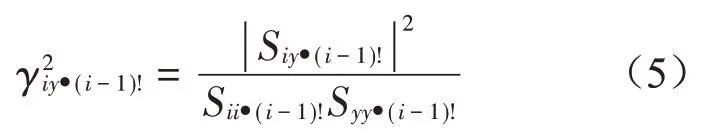
偏相干函数的条件谱密度
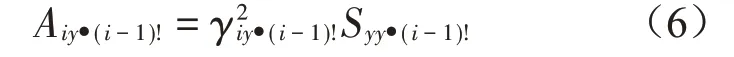
1.3 重相干分析
重相干函数提供了一组q个输入与输出之间的线性关系以及输入之间相关性的测量。重相干函数如下
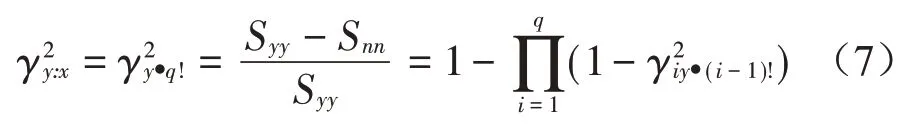
重相干函数的谱密度

在实际应用中,重相干函数可用于通过检查输入与输出之间的关系来确定输入中是否有重要信号源被遗漏。如果重相干函数大于0.8,则表示输出信号基本上是由输入信号决定的,没有信号遗漏;如果重相干函数小于0.8,则表示输出信号还受到其它信号影响,输入信号中有遗漏。这个应用在对各信号源特性不够了解的情况下是非常有用的。
2 船舶系统噪声源识别和分离方法
复杂船舶系统运行时,比如船舶汽机系统运行时,需要开启蒸汽系统提供能源,需要开启海水系统为其冷却,需要开启滑油系统为其润滑等,测试汽机系统振动噪声时,汽机系统不能单独开启,需要同时开启很多辅助系统设备,这时无法通过分步开启实现系统噪声源的辨识和分离等,建立复杂船舶系统噪声源识别和分离的方法,对于认识复杂系统噪声来源并针对有针对性的控制措施,具有重要意义。
2.1 船舶系统噪声源识别方法
一个振动系统具有三要素:系统特性、输入和输出,这三者相互联系,知其二,可求其三。噪声源分离就是在多输入单输出系统中判断哪个输入对输出的影响大。做系统振动噪声分离工作之前,需要确定系统的输入,系统噪声源的确定是一项细致的工作,确保系统输入没有遗漏,没有重复,具体来说作为系统噪声源要满足以下3个条件:
(1)完备性条件
分析模型选取的噪声源是否完备。检验选取的噪声源输入信号和输出信号的重相干函数是否足够大,如果被估计的重相干函数值小于0.8,则认为选取的噪声源时遗漏了作用大的噪声源,因而就应当重新清理潜在的噪声源,并加入到模型中去,再次做重相干分析,直到重相干函数大于0.8。
(2)相关性条件
分析各噪声源和输出的关系。把各噪声源和输出信号做常相干分析,若估计出相干函数非常小,则认为此噪声源对观察点的作用非常小,可判定为这个输入和输出没有关系,并把此噪声源从多输入模型中去掉。
(3)唯一性条件
确定各个噪声源之间的唯一性。估计各个噪声源之间的常相干函数,若其值远小于1,则认为这两个输入信号彼此独立,都是输入噪声源;若其值接近于1,则表示这两个输入相干性很强,可用其中一个噪声源代替另外一个噪声源,并将另外一个从多输入单输出模型中去掉。
上述3 个检验项目中,完备性条件是为了防止忽略贡献大的噪声源,相关性条件是为了去掉没有贡献的噪声源,唯一性条件则是为了去掉重复的噪声源。
2.2 船舶系统噪声源线谱分离方法
船舶机械系统噪声量级大小基本上由特征线谱决定,掌握特征线谱来源,就可以有针对性地采取控制措施,系统噪声源线谱分离流程如下:
首先,针对要分离系统的输出响应,确定系统的输入噪声源,系统输入噪声源按照上节的分析方法确定。
其次,提取输出信号自谱的特征频率。
(1)若输出信号的特征频率来自单个输入信号,则可以判定该特征频率来自这个输入;
(2)若输出特征频率来自多个输入,则输入信号之间要做常相干分析。
①如果相干系数小于0.2,则表明输入信号相互独立,输入分别和输出做常相干分析,输入和输出之间的常相干谱就是输入在该特征频率对输出的贡献;
②如果相干系数大于0.2,则表明输入信号相互有影响,输入分别和输出做偏相干分析:如果偏相干函数有大有小,则偏相干函数大的输入贡献大;如果偏相干函数都很大,则两个信号都有贡献;如果偏相干函数都很小,则说明只有一个信号贡献大,哪个信号贡献大需要根据实际系统因果关系判断。
最后,根据输入和输出信号的相干谱,分离输出噪声线谱的来源和贡献。
3 试验研究
3.1 试验系统描述
典型A 系统运行时,需要同时运行B、C、D 系统,A系统主要噪声源有A泵、A阀,B系统主要噪声源有B 泵,C 系统主要噪声源有C 泵,D 系统主要噪声源有D 泵。测试A 系统运行的噪声(记为系统的单输出信号)时,同时测量系统主要贡献源A 泵、A阀、B 泵、C 泵、D 泵的振动(记为系统的多输入信号)。测得A 系统运行时的噪声,主要有47 Hz、92 Hz、18 Hz、83 Hz 等特征线谱,其中47 Hz 线谱幅值最大,92 Hz线谱次之,18 Hz、83 Hz线谱再次之。下面采用本文提出的方法辨识A系统运行的噪声线谱中来自各台泵和阀的贡献。
3.2 试验系统噪声源确定
(1)噪声源完备性分析
初步选取A 泵、A 阀、B 泵、C 泵、D 泵作为潜在输入噪声源,开展输出噪声和所有潜在噪声源振动之间做重相干分析,重相干谱如图4。
从图4可以看出:在10 Hz~4 000 Hz 频段范围内,选取噪声源的重相干谱与输出信号自谱基本一致,主要频段重相干函数都在0.8 以上,说明选取的噪声源能够反映输出的信号特性,没有遗漏重要的噪声源。
(2)输入和输出相关性分析
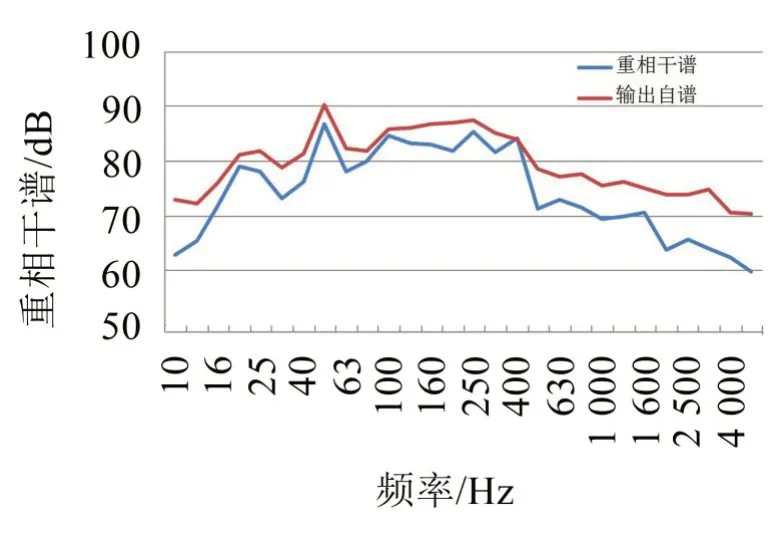
图4 典型系统潜在噪声源重相干谱和输出自谱图
利用潜在噪声源A 泵、A 阀、B 泵、C 泵、D 泵振动和输出噪声信号之间做常相干分析,相干系数都大于0.2,说明选取的噪声源和信号之间是相关的,对输出信号都有贡献。
(3)输入信号之间唯一性分析
利用潜在噪声源A 泵、A 阀、B 泵、C 泵、D 泵振动信号之间做常相干分析。泵与泵之间相干函数都很小,说明各泵之间是相互独立的;A泵和A阀振动加速度相干系数在特征线谱处都大于0.8,说明A阀振动是A泵引起的,A阀不能作为独立噪声源,需要将其从潜在噪声源里去掉。
通过对以上噪声源的完备性、相关性和唯一性分析,确定A系统运行时,主要噪声源有A泵、B泵、C泵、D泵。
3.3 试验系统噪声源分离
根据上节分析可知,A系统运行时,系统主要贡献源有A 泵、B 泵、C 泵、D 泵,噪声的特征线谱有47 Hz、92 Hz、18 Hz、83 Hz等。
(1)输入和输出信号谱分析
针对输入和输出信号开展谱分析,提取输出信号的特征线谱,查看系统主要噪声源中是否存在对应的特征线谱,如下表1所示。
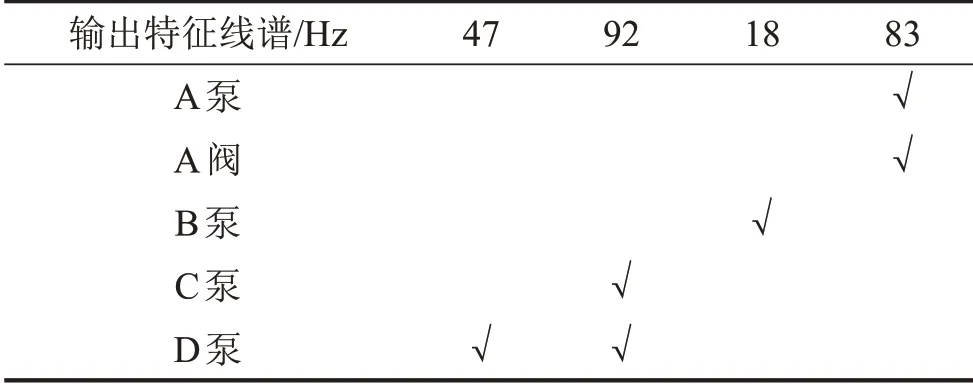
表1 输入和输出线谱比较
由表1可以看出:(a)47 Hz线谱来自于D泵;(b)18 Hz线谱来自于B泵;(c)92 Hz线谱来自于C泵和D泵;(d)83 Hz线谱来自于A泵和A阀。
(2)重复线谱输入的常相干分析
输入噪声源中重复的特征线谱有92 Hz 和83 Hz,其中92 Hz 线谱来自于C 泵和D 泵;83 Hz 线谱来自于A 泵和A 阀。对其做常相干分析,系数如下表2所示。

表2 重复线谱输入的常相干系数
由上表可以看出:
在92 Hz 特征线谱处,C 泵和D 泵相干系数为0.008,说明两者彼此独立,它们分别对输出的92 Hz线谱有贡献;
在83 Hz 特征线谱处,A 泵和A 阀相干系数为0.923,说明两者强相干,需要进一步做偏相干分析才能确定83 Hz特征线谱来自于哪个噪声源。
(3)相干特征频率处,输入和输出分别做偏相干分析
在83 Hz 特征线谱处,A 泵和A 阀强相干,根据系统实际运行状态,A 泵是基础源,A 阀是次生源,按照先后顺序,其分别对输出做偏相干分析,偏相干系数如下表。

表3 相干线谱输入和输出的偏相干系数
由表3可以看出:
在92 Hz特征频率处,C泵和D泵的振动与输出信号的偏相干系数分别为0.496 和0.512,即两泵分别独立对输出噪声92 Hz线谱有贡献;
在83 Hz 特征频率处,A 泵和A 阀强相干,和输出偏相干系数分别为0.748和0.132,说明输出83 Hz线谱主要是由A泵引起的,A阀的贡献较小。
(4)小结
由上述分析可知,典型系统特征线谱来源如下:
①47 Hz特征线谱来自于D泵;
②92 Hz 特征线谱来自于C 泵和D 泵,两者相互独立,都对系统运行时的噪声产生了较大贡献;
③18 Hz特征线谱来自于B泵;
④83 Hz特征线谱来自于A泵。
由于系统运行时47 Hz、92 Hz线谱较大,而根据相干偏相干分析47 Hz 线谱主要来源于D 泵,92 Hz线谱主要来源于C 泵和D 泵,所以D 泵和C 泵是该系统振动噪声控制的重点。利用本文提出的噪声源识别方法,提高了工程中振动噪声问题治理的效率和准确性。
4 结语
本文根据相干分析、偏相干分析和重相干分析理论,建立了船舶典型系统多噪声源工程识别方法和分离流程。
针对典型船舶系统噪声的辨识问题,应用建立的噪声源分离方法和流程,获取了噪声特征线谱的主要贡献源,排除了次生源的干扰,可满足船舶系统振动噪声问题诊断和控制的工程要求。研究表明,对于需同时运行多台泵且不能单独分步开启的复杂机械系统,本文建立的噪声源分离方法和流程,可以有效进行噪声线谱的分离和定位,对于认识噪声源及其传递特性,制定振动噪声控制措施具有重要的工程意义。

