小波阈值降噪技术对OPAX方法的改进研究
潘公宇,朱 瑞
(江苏大学 汽车与交通工程学院,江苏 镇江212013)
传递路径分析(Transfer Path Analysis,TPA)方法在对声振系统进行定量分析不同激励点的激励载荷,各传递路径的贡献量及其比例等方面具有广泛地应用。经过20多年的实践与发展,TPA理论已经趋于成熟,并且衍生出了多种以传统TPA 理论为基础的分析方法,比如快速TPA,多级TPA,工况传递路径分析(Operational Transfer Path Analysis,OPA),扩展工况传递路径分析(Operation Path Analysis with Exogeneous Inputs,OPAX)等[1]。其中,OPAX技术凭借其较高的识别精度,较低的建模成本等优势受到研究人员的广泛关注。该方法是在OPA 技术的基础上,利用参数建模的思想,对工况载荷进行识别,并辅以少量的频响函数,使得分析精度得以进一步提高,同时利用奇异值分解方法来解决OPA技术存在的路径输入信号之间的相互串扰问题。Janssens 等[2]于2011年提出OPAX 方法后,宋海生[3]深入研究了OPAX 方法的一般性理论,提出了模型质量的直接判据和间接判据,总结归纳出建模的经验公式,为该方法的应用奠定了理论基础。康菲等[4]利用OPAX方法,有效诊断出车辆在高速行驶时,驾驶员座椅处4阶噪声较大的问题来源。Rao等[5]利用OPAX 理论中的动刚度识别技术,识别了某全时四驱SUV 的悬置动刚度,用于传动系统的NVH 性能仿真。莫愁等[6]将逆子结构技术引入OPAX 理论中用于悬置动刚度的计算,进一步提高了其分析精度。
在计算OPAX 方法中的参数模型时,需要输入大量的工况数据,该数据是在汽车运行工况下采集的,由于道路的不平整,车辆偶发性抖动,信号波动等因素,采集到的信号难免会掺杂有其他干扰信号,这使得OPAX方法的最终计算结果与实测响应差距较大,会遗漏某些峰值响应,无法很好地表现出各传递路径的特性,与传统TPA 方法在精度上面存在差距。由振动传感器采集到的有用信号是随着时间变化,且有一定规律可循的,而其他干扰信号随机性很强,往往涵盖在有用的信号数据中,难以区分。因此,采用非线性处理方法来对采集到的信号数据进行消噪处理是非常合适的,这有利于进一步提高OPAX方法的计算精度。
在非线性处理方法中,相比于分析整个时域的傅里叶分析方法,小波分析能同时在时域和频域上实现高分辨率的局部分析[7],具有更灵活的多分辨率分析的时频分析特点,依据有用信号与干扰噪声信号在不同分辨率下分布特征之间的不同可以有效滤除噪声信号,保留标准信号特征[8]。本文基于小波阈值降噪方法,将从小波阈值和阈值函数两个方面为汽车工况数据降噪确定合适的算法,并将目标点处测量的响应信号,原OPAX方法的贡献量计算值,以及改进后的OPAX 方法的贡献量计算值进行比较,验证本文改进方法的有效性。
1 OPAX方法基本原理
TPA 理论最基本的分析模型可表示为“源—路径—响应”,在整车系统中,激励能量从动力总成等主动端开始,通过各物理连接件或空气等路径传递到目标点产生响应,其理论表达式如式(1)所示

其中:,Y(ω)表示某一目标点的总贡献量,ω为圆频率,n和m分别代表结构传递路径和空气传递路径的数量,Hi(ω)和Hj(ω)分别表示在某一频率下,结构传递路径和空气传递路径的频响函数,Fi(ω)和Qj(ω)分别表示振动载荷和声学载荷。本次研究主要是分析车辆的动力总成悬置系统,故不考虑空气传递路径部分。在传统TPA 理论中,辨识载荷的主要方法是逆矩阵法,该方法需要大量的振动数据,以此来解决可能出现的伪逆问题。该方法计算工作量大,分析周期长。而OPAX 方法则利用汽车工况数据易于采集的特点,大量采用工况数据进行参数化建模,求解载荷,如式(2)所示,该模型待求解的参数在频率上相互独立,简化为三个参数的函数。

式中:Ki(ω)=-miω2+jciω+ki。其中mi,ci和ki为待求解参数,分别代表弹性元件的动质量,阻尼和静刚度,Ki为动刚度,aai(ω)和api(ω)分别代表主动端和被动端的振动信号。将此模型替换掉传统TPA方法中,求解载荷的逆矩阵模型,则目标点的结构响应如式(3)所示
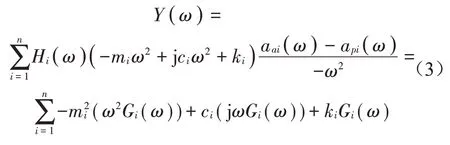
在车辆运行工况下,将采集到的数据做阶次切片,并根据每个阶次切片中转速采样点的个数以及相对应的振动加速度和频率值,求解出参数变量,辨识载荷,最终计算出各路径的贡献量。因此可将式(3)的结构响应变形为如下所示

式中:m为阶次切片的个数,r为每个阶次切片内转速采样点的个数。
2 小波阈值降噪算法的确定
小波阈值去噪方法是在小波分析理论的基础上发展而来的,在对含噪信号进行小波分解后,信号的有用成分和干扰成分的小波分解系数相差较大,通常具有较大的小波分解系数的信号为有用信号[9]。基于此,小波阈值降噪方法的核心思想便是确定适合于待处理信号的最优阈值,对比信号的小波分解系数与阈值,保留大于阈值的小波信号,剔除或者衰减小于该阈值的小波信号,最终利用小波分析理论,重构信号,完成信号降噪的过程。
2.1 小波阈值的构造
在小波阈值降噪方法中,小波阈值的选择决定了在小波分解中,信号是有用信号还是噪声干扰信号。阈值过大,会使信号中的有用信号受到扼杀,使得信号失真。相反,阈值过小,则会保留较多噪声信号,降噪效果不理想。目前较为通用的阈值为固定阈值[10],如式(5)所示
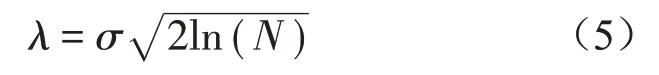
其中:N表示数据长度,σ为噪声的标准差,利用鲁棒中值算法来给出估计值,如式(6)所示

其中:ω为小波分解系数。显然,在使用通用阈值λ时,随着数据长度的增加,该阈值明显加大,并且不会根据各层小波系数的不同而做出相应的调整,自适应较差。为了解决这一弊端,考虑到各层小波分解系数的不同,噪声的频率特性也不同的特点,且噪声经小波分解后,其幅值随着分解层次的增大而减小,本文将分解层次作为调节各层预置阈值的调参数,改进原有的固定阈值,如式(7)所示
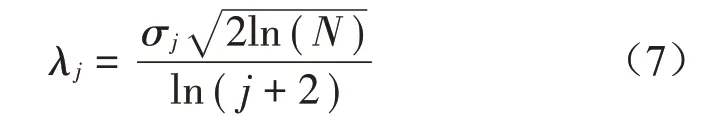
其中:j表示小波分解尺度。新构造的阈值可将原有固定阈值根据其分解尺度的不同,而做出相应调整,灵活性较大。
2.2 小波阈值函数的构造
目前运用较为广泛的阈值函数分别是软阈值函数和硬阈值函数。其中软阈值函数的估计小波系数与实际值偏差较大,使得重构后的信号会丧失信号的某些特征。硬阈值函数去噪效果较好[11],如式(8)所示,但是却会造成重构信号的不连续,影响后续研究。
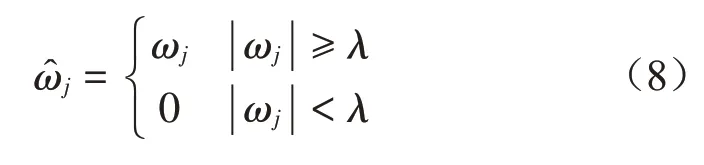
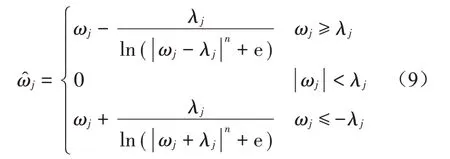
其中:n为调参数,且当n→∞时,该函数即为传统硬阈值函数。调节参数n的数值,可进一步调整重构信号与原始信号的逼近程度。当ωj=λj时,有ln(|ωj-λj|n+e)=1,显然因此该阈值函数在ωj=λj处是连续的,同理,该函数在ωj=-λj处也是连续的。如图1所示

图1 阈值函数曲线
图1展示了小波系数在-20 至20 之间,硬阈值函数以及n=2和n=8时的新构造阈值函数曲线,其中λ值取5,可以看出,新构造的阈值函数在λ=5 处,即临界阈值处,连续性更好,且当n值越大时,其函数值越逼近硬阈值函数,精度更高。
3 OPAX方法改进效果验证
3.1 OPAX模型建立及工况数据采集
试验对象为一款搭载1.5 t 四缸汽油发动机的乘用汽车,动力总成悬置共有3个,其中右侧发动机悬置为液压悬置,其余为橡胶悬置。悬置各主,被动端分别安装一个三向振动加速度传感器,用来测取振动输入信号,在车辆地板,方向盘以及驾驶员座椅导轨3个位置分别安装一个加速度振动传感器测取响应信号,各传感器安装位置如图2所示。

图2 传感器测点布置图
这样就形成了3×3=9输入、3×3=9输出的传递路径模型。试验过程中,选用3 档节气门全开工况,利用LMS 移动主机测取车辆在发动机转速为1 000 r/min 至4 000 r/min 状态下,各传感器获取的数据。
3.2 频响函数测取
在对整车进行频响函数测量时,为了避免各路径的相互耦合,提高测量结果的准确性,需将动力总成,悬置等部件拆除,用尼龙绳将整个车身吊起。保留工况试验时,悬置被动端以及各响应点,参考点处的传感器,利用力锤在悬置传感器附近施加激励,测取各传感器信号以及相应的传递路径频响函数信号。部分测试数据如图3所示。
图3(a)为频响函数幅值,图3(b)为对应的相干系数曲线。由图可知,在各频率段相干系数最小不低于0.85,整体趋近于1,表明本次测试结果可靠。
3.3 小波去噪效果验证
根据上述新构造的阈值,阈值函数,以及原OPAX方法的计算流程,现确定改进后的OPAX方法的主要步骤如下:
步骤1,信号小波分解:根据车辆工况数据的特征,选用匹配性更合适的小波基函数及相对应的分解层次,对待处理数据进行分解;
步骤2,小波分解系数的阈值量化:利用式(7)和式(8)分别计算估计阈值,量化数据分解后的小波系数,从而确定各分解层的新的小波系数;
步骤3,小波重构:对步骤2 中得到的新的小波系数进行小波逆变换,重构出新的去噪信号;
步骤4,计算贡献量:将去噪后的信号代入上述参数化模型,辨识载荷,从而计算各路径贡献量。
在选择小波基函数时,著名学者Ingrid Daubechies构造出一种具有紧支集的近似对称的小波函数[12],即Symlet 小波函数。该函数具有良好的正则性和对称性,在处理工况数据时,重构后的信号光滑性更好,相位失真的程度更低。本文采用sym5小波函数进行5层小波分解来对工况数据进行信号去噪,重构。
图4展示了动力总成左悬置被动端X向的振动幅值。
从图中可以看出,在时域数据中,去噪后的信号走势与原始信号波形基本一致,但是绝大部分的毛刺均已被剔除,曲线光滑连续,初步表明上述所构造的小波阈值去噪方法有效,但还需进一步验证其对最终贡献量的修正效果。
3.4 工况载荷识别

图3 动力总成右悬置被动端Z向—右悬置主动端X向和地板Z向频响函数
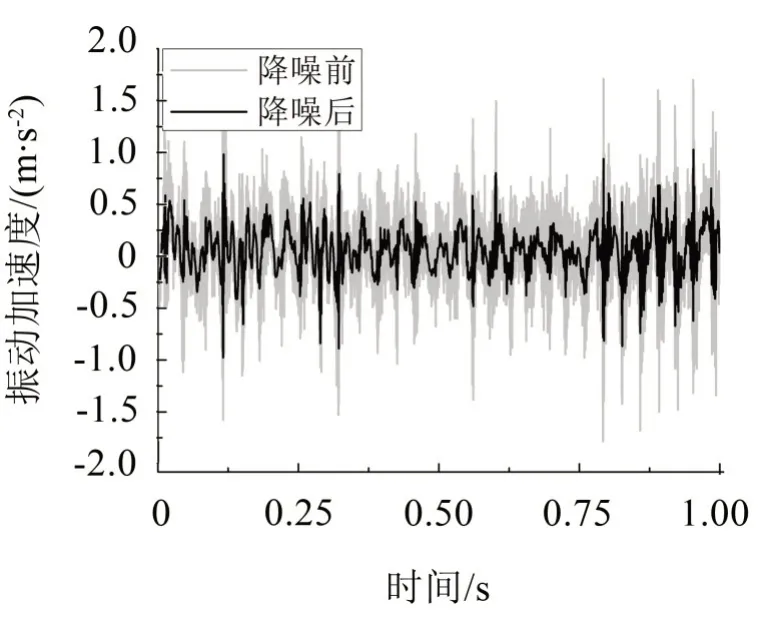
图4 左悬置被动端X方向时域图
车辆在3 档节气门全开的运行工况下,发动机激励能量经各悬置路径传递到整车,引起车内振动。由于数据较多,图5展示了在发动机2阶工况下,3个悬置路径处,振动能量最高的4 个方向的载荷识别结果。在1 700 r/min 至2 700 r/min 之间,右悬置X向和后悬置X向的载荷变化范围较小,在超过2 700 r/min 时,右悬置X向载荷逐渐增大。右悬置Y向和左悬置Z向在整个转速范围内载荷始终处于上升趋势。故在后期悬置匹配优化时,应格外关注右悬置X向,右悬置Y向和左悬置Z向3 个方向的悬置动刚度。
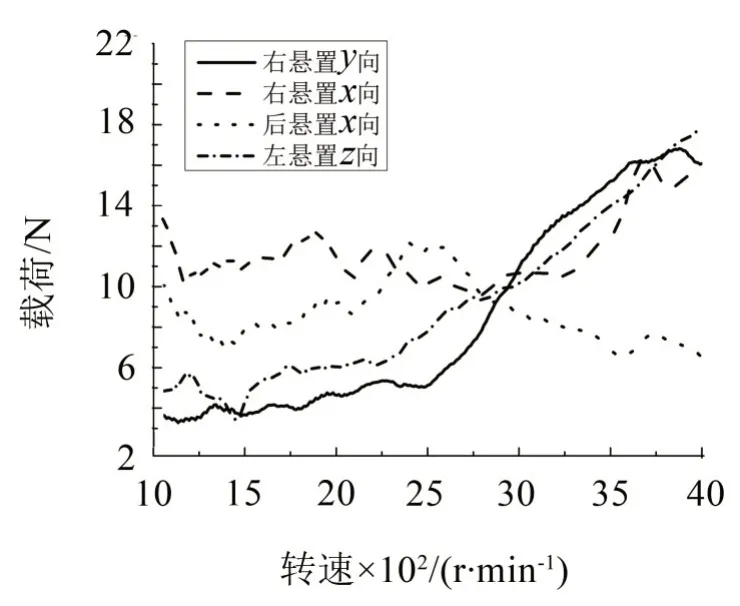
图5 动力总成悬置2阶工况载荷
3.5 OPAX方法的计算贡献量比较
为了评价新的降噪算法的去噪效果,研究人员一般采用信噪比(SNR)和均方根误差(RMSE)来进行评估。这两项指标考察的是去噪后的信号与原信号之间的偏差,其中信噪比越大,均方根误差越小,信号的去噪效果越好。考虑到OPAX方法的最终目的是计算得到目标点处的贡献量,计算值与实测值越接近,模型建立地就越准确,信号的去噪效果越好。因此,本文将目标点处的实测值作为标准信号,分别采用软阈值函数,硬阈值函数,以及本文新构造的阈值函数,对比验证本文方法的优越性及准确性。
图6分别示出了在发动机2阶情况下,地板Z向振动实测值,以及分别采用软阈值函数,硬阈值函数和新阈值函数去噪的贡献量计算值。总体上,4 种方法所得结果走势与实测值基本一致,但是在采用小波阈值降噪方法后所得结果与实测值吻合程度更高,在频率段75 Hz至125 Hz内尤其明显。
表1列出了上述4 种方法相对于实测值的信噪比和均方根误差。从表中可以看出,在采用小波阈值降噪方法以后,计算结果的信噪比增大,均方根误差变小,且相比于软阈值函数和硬阈值函数,新阈值函数所得结果的信噪比最大,达到11.468 5,均方根误差最小,为0.015 8,这说明本文所构造的新阈值函数有利于OPAX方法的精度提高。

表1 不同阈值函数降噪后SNR和RMSE比较
在频段75 Hz至125 Hz内,振动响应较大,且有4个比较明显的响应峰值,这也是工程人员最关心的部位。
表2列出了在4处峰值频率处,计算值和实测值之间的相对误差。由表中可以看出,改进后的OPAX 方法的相对误差均能控制在10%左右,属于可接受范围,改进后所得结果的精确性得以进一步提高。

图6 发动机2阶情况下地板Z向振动贡献总量比较

表2 2种方法的峰值相对误差比较
虽然改进后的OPAX 计算结果更接近测量值,但是仍然存在一定的误差,考虑到采集仪器,传感器,以及其他的非线性因素等难以避免的误差外,遗漏路径可能是最大的问题。由于OPAX方法的主要测试条件是3档节气门全开工况,在此工况下,其对车内的振动传递路径除了3 个悬置方向,还包括排气管吊耳,变速器齿轮,以及路面对轮胎的部分振动传递路径等。本文OPAX实验的主要目的是分析评价悬置系统的隔振性能及其对车内振动的贡献,且改进后的OPAX 方法计算值与实测值趋势基本一致,精度更高,这有利于减少后期对悬置性能进行评价的误差。
4 结语
针对OPAX 方法的预测精度问题,和传统TPA理论相比,由于OPAX方法主要采用的是工况数据,且为了模拟更真实的振动响应,多采用室外运行工况,这就不可避免地会掺杂许多不相关的干扰信号。本文针对OPAX 方法的这一特点,构造新的小波估计阈值和阈值函数,将新构造的小波阈值降噪算法和OPAX方法相结合,得出如下结论。
(1)将小波阈值降噪技术引入扩展工况传递路径分析方法中,并构造了新的小波估计阈值与阈值函数,提出了具体的操作流程。
(2)在采用新构造的小波阈值降噪算法对动力总成悬置处的信号进行降噪处理后,重构信号的走势与原信号基本一致,但是波形更加光滑,降噪效果明显。
(3)在贡献量计算方面,和原有OPAX 方法相比,改进方法的贡献量计算值更接近于实际测量值,且在各峰值处的相对误差更低,预测精度得以进一步提高。

