初中生逻辑推理的测验研究
严 卿,黄友初,罗玉华,陈 昊,喻 平
初中生逻辑推理的测验研究
严 卿1,黄友初1,2,罗玉华3,陈 昊4,喻 平1
(1.南京师范大学 课程与教学研究所,江苏 南京 210097;2.上海师范大学 教育学院,上海 200235;3.江苏第二师范学院 教育科学学院,江苏 南京 210013;4.华东师范大学 数学科学学院,上海 200241)
基于逻辑学对于推理的分类以及心理学关于推理能力的研究成果,对国内外的逻辑推理评价研究进行梳理,结合中学数学知识的特点,提出一个测量初中生逻辑推理能力的框架,据此编制测验题.测验兼顾推理的形式与内容两方面.通过探索性因素分析检验测验的结构效度并进行修订,修订后的维度包括简单推理、选言推理、命题演算、假言推理、合情推理,其中前4个同属演绎推理.测验具有较好的结构效度和信度.
逻辑推理;数学命题;核心素养
《普通高中数学课程标准(2017年版)》(以下简称“2017版标准”)中提出了6个数学核心素养:数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析.按照教育部的要求,要以这些核心素养为主线,贯穿于整个课程、教材和教学之中.于是,如何评价学生的核心素养,如何考察学生核心素养的发展水平,就成了迫切需要研究的课题.
1 问题提出
其实,6个数学核心素养就是6种数学能力或者说关键能力,因而需按照能力研究的思路和方法,对其评价进行探究.这里仅探讨6个关键能力中的逻辑推理.
“2017版标准”中对其的定义为:“逻辑推理是指从一些事实和命题出发,依据规则推出其它命题的素养.主要包括两类:一类是从特殊到一般的推理,推理形式主要有归纳、类比;一类是从一般到特殊的推理,推理形式主要有演绎.”[1]对于逻辑推理的概念,存在着不同看法.在逻辑学中,推理是“由一个或一组命题(前提)推出另一个命题(结论)的思维形式”,其中“逻辑推理是保持真值的推理”[2],即认为逻辑推理特指演绎推理.实际上,“2017版标准”中的“逻辑”一词强调的是在推理过程中“关系”和“性质”的传递[3],而非“正确性”和“有效性”.这样的定义虽然不同于传统的理解,但是深化了对归纳、类比推理中所蕴含规则的认识,抓住了其与演绎推理的共性.此外,虽然逻辑学和数学中都会用到“逻辑推理”一词,但形式逻辑中关心的是“推理形式是否合乎逻辑规则”[4],而在数学背景下讨论逻辑推理,则需要兼顾两方面:内容上的数学命题,形式上的逻辑规则.
推理能力一直是心理学关注的问题,研究集中在三段论、假言推理、选言推理等演绎推理上[5],研究方法主要采用测量,量表的内容是针对一般的推理而很少涉及数学知识.演绎推理的进一步研究涉及心理模型理论和脑机制研究[6–7].
综观数学教育领域中推理的评价研究,简单而言可以分为两类.一类研究将推理能力发展水平作为基本框架,为此设计出不同复杂程度的测试题用于评价,区分复杂程度的标准往往是解决问题时需要用到的推理的次数;另一类研究则首先依据推理类型进行分类,进而设计不同类型的问题.虽然有的研究兼具这两个方面,但往往对其中之一更加侧重.实际上,这反映了评价推理能力的两种倾向——前者侧重于运用推理解决问题的能力,使用的问题更接近于通常意义上的数学题(典型的例如证明题),往往需要运用多次推理,但并不关注推理的具体逻辑形式;后者对推理的考查更直接、具体,关注推理的不同逻辑形式间的差异,或学生对某一具体逻辑形式的理解,类似于心理学的研究模式.这一区分在演绎、归纳、类比推理的评价研究中都有所体现.
在对演绎推理能力的研究中,克鲁捷茨基使用了“证明题”“要求理解和逻辑推理的题目”等题型[8];Senk研究了美国中学生在几何证明中的演绎推理能力[9];Peressini等建立了一个4步骤框架,用来评价学生在解答熟悉的现实背景问题时表现出来的数学推理能力[10].另一方面,Hoyles和Küchemann考察了学生对假言命题的认识、对假言推理的直接运用以及对假言命题的证明(证伪)[11];美国全国教育进展评估项目(NAEP)中,包括了选择给定命题的反例、对于公理和定理的理解、现实背景的逻辑问题等[12];Jansson研究了初中生在假言命题、选言命题、联言命题、否命题等不同逻辑形式的任务上发展的先后层级[13].
对于归纳推理,林崇德将小学运算中归纳推理能力区分为直接归纳和间接归纳推理[14].类似的,田中等将归纳推理划分为一步推理和二步推理[15].显然,这些都并未深入考察归纳推理的具体形式,而更看重在解决不同复杂程度问题时运用归纳推理的能力.另一些研究则对归纳推理的形式进行了细致的划分.例如Christou等把归纳推理区分为2种类型(属性归纳和关系归纳)和3种过程(识别相似性、识别差异性以及综合)[16];Radford指出应当区分尝试错误型的归纳和发现规律的归纳[17].此外,有的研究采取了纵向的划分.Styliandes把归纳推理的过程区分为了两个阶段[18]:识别模式和提出猜想,前者只需符合所给的有限信息,是绝对正确的;后者则超越了给定信息,是一种推测,有待验证.武锡环、李祥兆按照归纳推理的认知过程划分为信息表征、归纳识别、形成猜想、假设检验4个阶段,并以此为框架编制测验[19].
对于类比推理的评价,常用的问题形式有两种:问题解决中的类比、经典类比问题.前者需要被试在原问题和靶问题的结构间建立一种联系,利用对原问题的理解来解决靶问题,后者指形如A︰B︰︰C︰D(例如树︰树枝︰︰身体︰胳膊)的问题[20].显然,这一区分同演绎推理、归纳推理中的区分十分相近.Alexander等使用经典类比问题构造了类比推理测验,并用于研究类比推理和数学推理间的关系[20].
总结已有研究,可以发现几个问题.第一,心理学的研究比较成熟,研究方法规范,但是研究范围主要是一般的推理而不太关注数学中的逻辑推理;第二,数学教育领域对逻辑推理的评价研究中,很少看到测量工具的详细编制过程,而且许多研究的样本数量偏小;第三,许多智力测验量表都是把逻辑推理作为子量表,例如韦克斯勒量表、斯坦福—比纳量表等,缺少专门针对初中生逻辑推理的测验量表.
遵循推理评价研究的两种基本倾向,具体的研究思路如下.第一,编制一套测量初中3个年级逻辑推理的工具,这个工具偏重测量学生的形式逻辑思维,涉及的数学知识不超出初一教材水平,记为测验A.这个测验可用于初中生(数学背景中)逻辑推理的发展研究.第二,编制初中每个年级的数学推理测验B1、B2、B3,这3套测验题分别以本年级的数学知识为基础编制,偏重于考察逻辑推理在数学问题解决中的运用,故使用“数学推理”以示区别,分为知识理解、知识迁移、知识创新3级水平[21],在关键能力层面考察每个年级学生的数学推理水平.第三,考察测验A与测验B1、B2、B3之间的关系,即学生的逻辑推理与数学推理的关系.这里只研究测验A.
2 测题编制
2.1 因素初步拟定
首先,根据“2017版标准”的定义,可以将逻辑推理分为从一般到特殊的演绎推理,以及从特殊到一般的归纳、类比推理,即合情推理.这也符合传统上的分类.
进一步地,演绎推理可以区分为两个层面——命题与推理.推理由命题组成,能够推理的前提是理解命题,命题的不同也决定了推理类型的不同.命题在数学学习中广泛存在,概念、定理是命题,证明题即是解释一个命题何以为真.结合形式逻辑中对命题的分类,这里把命题层面分为简单命题与复合命题,前者主要是性质命题,后者包括合取式(联言命题)、析取式(选言命题)、蕴含式(充分条件假言命题)、等值式(充分必要条件假言命题)、否命题(包括简单命题与复合命题的否定)5种命题演算.
推理层面维度的选取和命题层面保持一定的对应关系.由简单命题构成的推理是三段论,复合命题中的析取式构成选言推理,蕴含式构成假言推理,这3种推理组成了推理层面的基本分类.这几类推理在中学数学中十分常见,同时在心理学关于推理的研究中也占据了重要的位置.进一步分析,对简单命题的考察不可避免涉及性质命题的直接推理,这与三段论同样都是基于性质命题的推理,因此将它们纳入同一个维度也是合理的,称为简单推理.至于合取式构成的联言推理,其推理形式和对应的命题演算形式差别极小,因此不再另作考虑.
对于归纳推理,借鉴Christou等的框架,包括属性归纳和关系归纳两类[16].对于类比推理,采用评价类比推理的两种常用问题模式:经典类比问题和类比问题解决.
基于以上分析,逻辑推理测验由演绎推理和合情推理两个分测验组成,其中演绎推理分为简单推理、命题演算、选言推理、假言推理等4个子测验,合情推理分为归纳推理、类比推理两个子测验.以上分析的过程本身也显示出推理形式间复杂的关系,这一框架是否合适还依赖于因素分析的检验.
2.2 编制题项
设计题项的内容,要考虑问题的知识背景.在心理学关于逻辑推理的研究中,问题背景始终是一个重点变量,这反映在很多研究中,这些背景涉及熟悉与不熟悉[22].具体与抽象,几何与算术,与常识冲突的背景,假想背景等[23].为了使测验能适用于初中3个年级,研究中涉及的数学知识不超出初一年级教材的水平.为了探索学生在解答数学背景推理问题时是否存在某种特殊性,作为对照,也考虑设置现实背景和不具有意义的符号背景问题.
根据初步拟定的初中生逻辑推理能力评价框架,在每个维度编制题项.题项的编制参考国内外文献及其中的量表、相关领域书籍中的典型例题、近年来的中考题等[4,11],全部采用选择题的形式.邀请数学教育专业教授、研究生分别对每个维度的题项进行讨论、筛选,获得27道题的初始测验.初拟的6个维度题项数量分别为:简单推理6道,命题演算6道,选言推理4道,假言推理3道,归纳推理4道,类比推理4道.其中数学背景题15道,现实背景9道,符号背景3道.该测验记为测验1,结构见表1.下面以一道题为例,对所编制的题项进行介绍.
例:如果两个长方形的长与宽分别相等,那么它们的面积相等;现在长方形与长方形的面积相等,则一定有( ).
A.它们的长与宽一定分别相等
B.它们的长与宽可能都不相等
C.它们的长一定相等
D.它们的宽一定相等
该题在形式上属于假言推理,内容上涉及长方形面积.正确的(充分条件)假言推理形式有两种:如果肯定前件就肯定后件,如果否定后件就否定前件,而否定前件或肯定后件都无法做出确定的推理.初中生并没有接受过形式逻辑的训练,不可能自觉运用逻辑规则得到结果,因此做出选择需要依靠数学知识,测验中的大多数数学背景问题都具有这一特点.与此同时,逻辑因素也在发挥着作用.首先,虽然不同于标准的形式逻辑,但初中生拥有一套经验的法则,这套法则会影响到他们的判断,具体到该题中,一些学生可能会倾向于认为“如果肯定后件,就肯定前件”.其次,题干的表述采取的是假言命题的形式,理解假言命题是做出正确选择的必要条件.从而,测验题考查的既非纯粹形式逻辑,也非纯粹数学知识,而是数学知识与逻辑的综合运用,体现了数学中推理的特点,又由于测验中涉及到的数学知识比较简单,更多是反映出学生形式逻辑方面存在的问题.
评分标准为每题有两个答案或者每题有两个括号的,每个答案计1分;每题只有一个答案的计2分.
3 测题修订
3.1 样本
研究先后调查了两组样本.第1次测试:选择样本1为预测样本,在江苏、浙江的两所初中发放测试卷222份,删除空白或有较多题项未作答、回答呈现规律性的试卷后,回收有效试卷211份.其中初一79份,初二95份,初三37份;样本中男生110人,女生101人.第2次测试:选择样本2为再测样本,主要来自江西、江苏两省中有代表性的3所初中,其中一部分为通过网络测试的形式收集的南京地区样本.由于样本2的施测时间正值9月初,考虑到初一学生刚升学不久,因此仅在初二、初三年级发放试卷.回收有效试卷503份,其中初二236份,初三267份;样本中男生246人,女生257人.
3.2 数据处理
使用SPSS19软件进行数据管理及项目分析、探索性因素分析和信度检验.
3.3 预测与修订原始测验
第一,采用测验1对样本1进行测试,对测试数据依次进行项目分析与探索性因素分析,删除10道题后,得到一个5因素的结构.虽然该结果与理论框架较为一致,但存在一些缺陷.首先,部分因素题项较少.探索性因素分析的结果一般要求单个因素的题项数目至少为3,而结果中的假言推理、归纳推理维度都仅有两道题.其次,删除题项数量偏多,剩余的题项作为一个测验数量稍显不足.
由于因素分析的过程主要依靠数据驱动,研究者决定对所删除的题项重新进行审视,判断这些题项究竟是否存在问题.因此,邀请数学教育专业教授、初中数学教师围绕题项内容再次进行讨论,综合考虑内容的全面性、表述的适切性等因素,在所删除的10道题中,对4道题进行了修改,并重新编制了1道题替换原题项,剩余5道仍然保留.以t8为例,原题干为“如果生物体有生命活动,那么生物体必然有呼吸运动;乳酸菌是一种生物,适合在无氧条件下生存.据此可以推断( )”.该题考查假言推理,但涉及的知识点学生比较陌生,语言表述脱离日常习惯,实际上考查的可能并非推理能力,因此将题干简化为“如果生物要生存,就需要进行呼吸运动;乳酸菌是一种生物,可以在无氧条件下生存.根据以上描述,可以推断( )”.又如,原t20为“观察下列算式:21=2,22=4,23=8,24=16,25=32,……根据上述算式的规律,请你猜想210的末位数字”.该题考查学生的归纳推理,但即便不使用归纳推理,直接计算也能得出答案,因此将“210”修改为“22017”.修订后的测验依然有27道题,记作测验2.
第二,采用测验2对样本2进行测试.
3.4 项目分析
对测试2的数据进行项目分析.首先,作鉴别度分析.依据总分高低把样本分为3组,每组各占总人数的三分之一.运用独立样本检验,求出高分组和低分组样本在每道题得分上的均值差异,规定显著性水平为0.01.结果表明:所有题项的差异均达到显著水平.其次,作同质性检验.分别计算每道题与总测验得分、所属分测验得分的积差相关系数,结果表明:所有题项与总测验及所属分测验得分都在0.01的显著水平上相关,从而保留全部题项.
3.5 效度分析
3.5.1 结构效度
结构效度指能够测量出理论的特质的程度.对测验进行探索性因素分析,可以抽取测验的共同因素,通过与理论建构的维度比较,达到检验测验结构效度的目的.由于演绎推理与合情推理的划分在理论上已十分明确,因此分别对这两个分测验进行探索性因素分析.
(1)演绎推理分测验的探索性因素分析.
首先,通过计算发现取样适当性指标为0.926,Bartlett球形度检验统计量为2=2 810.696,=0.000,数据非常适合进行因素分析.其次,采用主成分分析法提取因素,考虑到预设的维度之间具有相关性,选择斜交旋转法对因子进行旋转.若规定基于特征值提取因素,按照特征值大于1的标准,只能提取3个因子,解释变异量46.1%.另一方面,因素数量的选择也要考虑到解释变异量的百分比以及自身的理论建构[24].结合理论建构与预测的结果,固定提取4个因子,再次进行探索性因素分析.删除在两个及以上因素都有较高负荷的题项,删除共同度低于0.3的题项,因此逐个删除t4、t7、t8、t9等4题.最终保留15题,解释变异量达到58.6%,题项的因素负荷全部大于0.5,共同度基本都大于0.4,详细结果见表2.
对因素进行命名.因素1的题项来自选言推理维度,因素2的题项来自命题演算维度,这两个因素直接沿用维度名称.因素3中,t1、t2考查的是简单命题,t3、t5属于三段论推理,故该因素命名还是用简单推理.因素4中,t10、t11都来自假言推理维度,t19虽然来自命题演算维度,但考察的是假言命题的否定,归入假言推理维度中也是合理的.总体而言,探索性因素分析的结果和预先建构的结构基本一致,说明演绎推理分测验具有较好的结构效度.
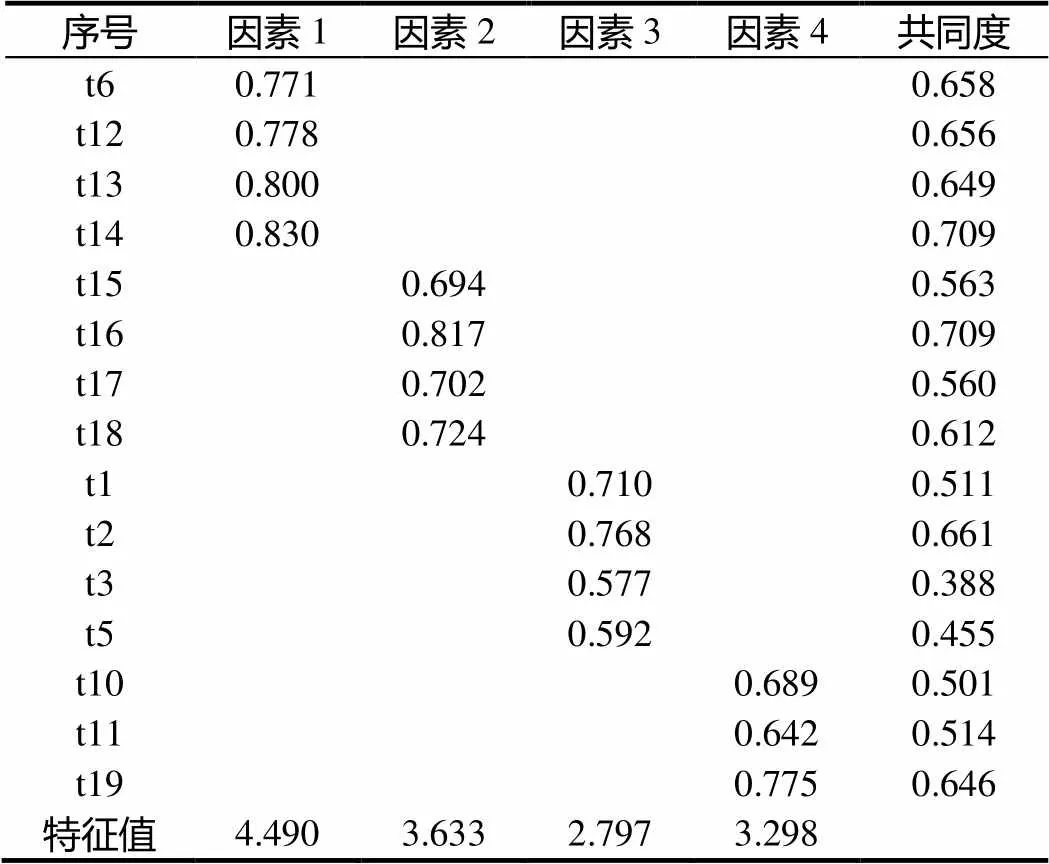
表2 演绎推理分测验的探索性因素分析(N=503)
(2)合情推理分测验的探索性因素分析.
取样适当性指标为0.851,Bartlett球形度检验统计量为2=644.779,=0.000,数据适合进行因素分析.采用主成分分析法提取因素,考虑到预设的维度之间具有相关性,选择斜交旋转法对因子进行旋转.若规定基于特征值提取因素,按照特征值大于1的标准,提取1个因子,解释变异量36.8%.根据理论框架,合情推理应当包括归纳和类比推理两个维度.因此,在固定因子数量为2的情况下再次尝试探索性因素分析.结果显示在两个因素中都混合有归纳和类比推理的题项.从而,不再区分合情推理的两个维度,并删除因子载荷及共同度最低的t22,再次进行探索性因素分析,解释变异量提升为39.7%.保留剩余的7道题作为合情推理维度,7道题的因子载荷都接近或大于0.6,表示抽取出的共同因素可以有效反映7个指标变量.详细结果见表3.
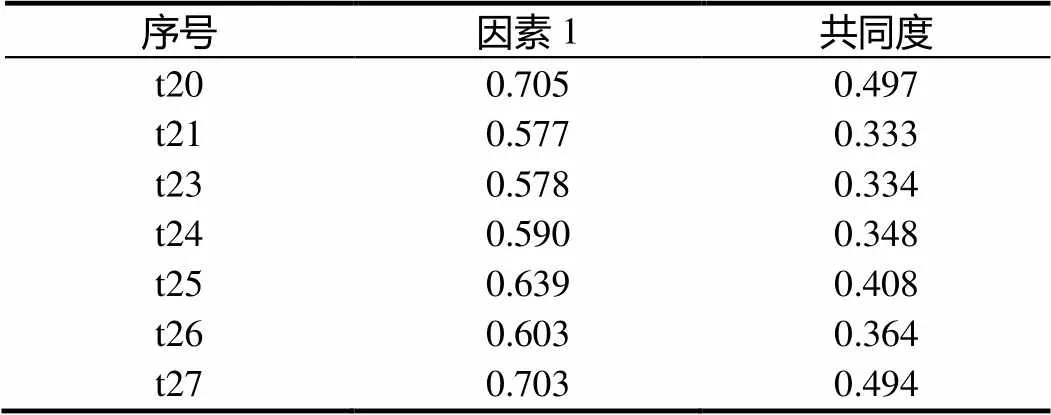
表3 合情推理分测验的探索性因素分析(N=503)
(3)总测验的结构效度分析.
以上分别检验了演绎推理与合情推理这两个分测验的结构效度,接下来运用相关系数法对二者合并而成的总测验的结构效度进行分析.将演绎推理的4个子测验得分相加,得到演绎推理维度分数,并考察各子测验、分测验、总测验之间的相关系数,详细结果见表4.可以看出,演绎推理内部4个维度间的相关系数小于各自与演绎推理间的相关系数;演绎推理内部4个维度与演绎推理间的相关系数,除命题演算略小外,大于各自与总测验的相关系数;演绎推理与合情推理间的相关系数小于各自与总测验的相关系数.从而,总测验具有较好的结构效度.
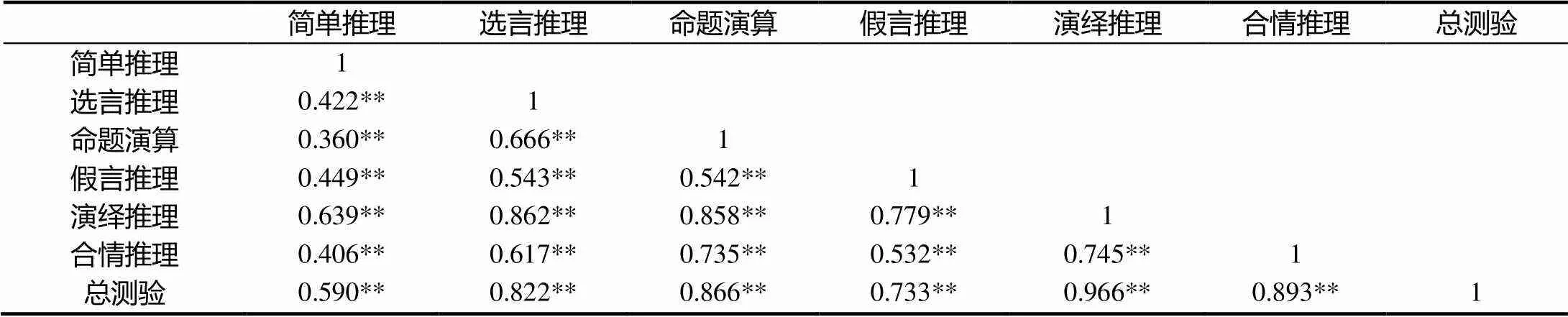
表4 各分测验及总测验的相关系数矩阵
注:表中**表示在0.01水平上具有显著相关性
由于对测验作探索性因素分析得到的结果与事先设计的理论框架高度吻合,因此不再对其作验证性因素分析.
3.5.2 内容效度
内容效度指测验题目的适切性与代表性,即测验内容能否反应所要测量的心里特质,以题目分布的合理性来判断.研究者主要从两个方面来确保测验的内容效度.一方面,测验题具有较好的代表性.研究基于逻辑学、心理学的研究成果提出了一个评价初中生逻辑推理的框架,在此基础上编制题项,不仅全面地考查到了各种推理形式,而且也兼顾了不同类型的问题背景,因此能够全面反映出学生的逻辑推理能力.另一方面,在测验的编制、修订过程中邀请专家参与研讨.参与者包括数学教育专业教授、研究生,以及一线初中教师等,分别从不同角度对题项的取舍提出了意见.例如部分题项背景对学生来说存在理解困难,不一定能考查到所设想的推理要素,表述较繁,等等.测验2正是在测验1预测的基础上,基于专家的意见修订形成.
3.6 信度分析
信度是对测量一致性程度的估计.对各子测验、分测验及总测验分别计算克伦巴赫系数,结果见表5.演绎推理与其各子测验的内部一致性系数在0.549~0.868之间,除了简单推理略低外,其余维度内部题项都有较高的同质性程度;合情推理的内部一致性系数为0.737;总测验的内部一致性系数为0.898.总体而言,编制的逻辑推理测验具有较高的信度.
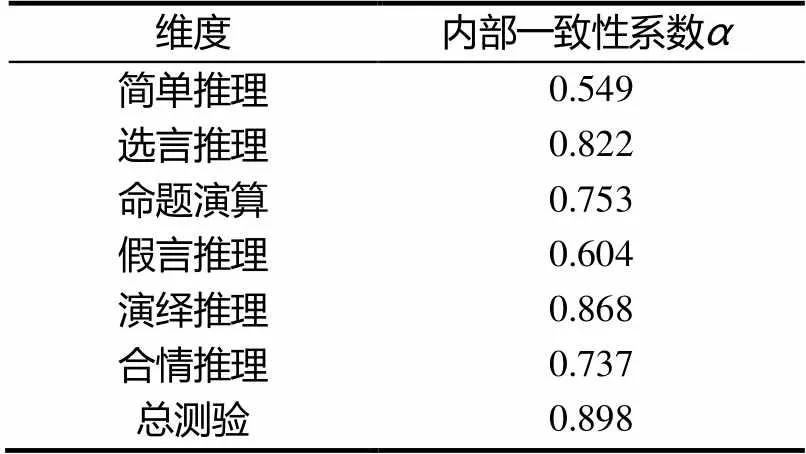
表5 逻辑推理测验各维度信度
最终版的逻辑推理测验题包含5个维度,总计22道题.题项分布见表6.测题见附录(总分44分).

表6 初中生逻辑推理能力测验题结构及题项分布
4 讨论与结论
4.1 测验框架的构建
在6个数学核心素养中,逻辑推理、数学运算、直观想象这3种能力具有一般性.事实上,这是传统意义上的数学3大能力,它们的一般性表现在几乎整个学习活动之中.其中逻辑推理和直观想象更具共性,它们可以脱离数学材料而独立地表现出来,自然科学和人文社会学科都需要这两种思维.因此,研究逻辑推理和直观想象,可以从两个层面切入,先探讨共性再研究特性.研究者所编制的测验偏重对逻辑推理共性层面的考查,亦即关注推理的逻辑形式,在内容上则以较简单的数学知识为主.
当前的许多研究都是就某一种逻辑形式开展的.李丹等人研究了小学生关于三段论推理的发展情况,采用的方法是由主试把三段论的两个前提念给被试听,然后要求被试说出结论,主要是考察被试的反应类型[5].胡竹菁等人对中学生三段论推理的现状作了调查,问卷由20道第一格至第四格的范畴三段论题目组成,主要考察从初一到高三年级学生三段论推理水平的发展以及性别差异[5].李丹等人研究了小学三年级到初中三年级学生的假言推理发展水平;吴荣先对小学三年级到初中三年级学生作了选言推理的研究[5].与这些研究不同,研究者将各种逻辑形式作为一个整体设计,基于数据得到了一个包含简单推理、选言推理、假言推理、命题演算、合情推理的初中生逻辑推理框架.这不仅可以对学生的逻辑推理进行全面考察,同时可以比较学生在逻辑推理不同维度上的发展差异.
4.2 测验的信效度
探索性因素分析的结果与理论框架基本一致,表明测验具有较好的结构效度,证明了基于推理形式的框架这样一种心理特质的存在.对于归纳推理与类比推理,分别都进一步分为两类来编制题项,这种过细的划分或许导致了二者难以形成两个独立的维度,也反映出合情推理的这两个类型间确实存在着紧密的联系.信度方面,简单推理维度的内部一致性系数略低,这反映出简单命题与三段论作为同一个维度虽然是合理的,但依然存在着某些差异.其余维度及总测验都有较高的信度.总体而言,测验结构基本合理,并具有较好的内部一致性,可作为初中生逻辑推理能力评价的工具.
4.3 研究的局限性
研究也存在一些问题.第一,简单推理的两道三段论都属于三段论的第一格,相对于第二格或第三格,在推理方面较为简单.一般说来,三段论的第二格与第三格应当在测验中有体现,这个问题需要在进一步的修订测验中加以解决.第二,表4中演绎推理与命题演算的相关略小于命题演算与总测验的相关,这是一个缺陷,但对整个测验没有产生太大的损害.第三,王光明教授等在数学学习策略问卷编制中,对量表作了验证性因素分析,这是一种更严谨的做法[25-42].研究者没有做这个工作,是由于探索性因素分析得到的数据与事前的理论建构高度一致,故省略了验证性因素分析.
[1] 中华人民共和国教育部.普通高中数学课程标准[M].北京:人民教育出版社,2017:5.
[2] 彭漪涟,马钦荣.逻辑学大辞典[M].上海:上海辞书出版社,2010:317.
[3] 史宁中.试论数学推理过程的逻辑性——兼论什么是有逻辑的推理[J].数学教育学报,2016,25(4):1-16,46.
[4] 华东师范大学哲学系逻辑学教研室.形式逻辑[M].上海:华东师范大学出版社,2016:2-6,89-98.
[5] 胡竹菁.演绎推理的心理学研究[M].北京:人民教育出版社,2000:216-228.
[6] 毕鸿燕,方格,王桂琴,等.演绎推理中的心理模型理论及相关研究[J].心理科学,2001,24(5):595-596.
[7] 杨群,邱江,张庆林.演绎推理的认知和脑机制研究述评[J].心理科学,2009,32(3):646-648.
[8] 克鲁捷茨基.中小学数学能力心理学[M].李伯黍,洪宝林译.上海:上海教育出版社,1983:155-159,181-185.
[9] SENK S L. How well do students write geometry proofs [J]. Mathematics Teacher, 1985, 78 (6): 448-456.
[10] PERESSINI D, WEBB N. Analyzing mathematical reasoning in students’ responses across multiple performance assessment tasks [C] // STIFF L V, CURCIO F R. Developing mathematical reasoning in grade K-12. Reston VA, 1999: 156-174.
[11] HOYLES C, KUCHEMANN D. Students’ understandings of logical implication [J]. Educational Studies in Mathematics, 2002, 51 (3): 193-223.
[12] HARELl G, SOWDER L. Toward comprehensive perspectives on the learning and teaching of proof [C] // LESTER F. Second handbook of research on mathematics teaching and learning. Information Age Publishing, 2013: 24.
[13] JANSSON L C. Logical reasoning hierarchies in mathematics [J]. Journal for Research in Mathematics Education, 1986, 17 (1): 3-20.
[14] 林崇德.学习与发展:中小学生心理能力发展与培养[M].北京:北京师范大学出版社,1999:347.
[15] 田中,徐龙炳,张奠宙.数学基础知识、基本技能教学研究探索[M].上海:华东师范大学出版社,2003:98-99.
[16] CHRISTOU C, PAPAGEORGIOU E. A framework of mathematics inductive reasoning [J]. Learning & Instruction, 2007, 17 (1): 55-66.
[17] RADFORD L. Algebraic thinking and the generalization of patterns: a semiotic perspective [C] // ALATORRE S, CORTINA J L, Sáiz M, et al. Proceedings of the 28th Conference of the International Group for the Psychology of Mathematics Education. North American Chapter, Mérida, 2006: 2–21.
[18] STYLIANIDES G J. An analytic framework of reasoning-and-proving [J]. For the Learning of Mathematics, 2008, 28 (1): 9–16.
[19] 武锡环,李祥兆.中学生数学归纳推理的发展研究[J].数学教育学报,2004,13(3):88-90.
[20] LYN D. English. Mathematical and analogical reasoning of young learners [M]. Lawrence Erlbaum Associates, Mahwah NJ, 2004: 47-74.
[21] 喻平.数学核心素养评价的一个框架[J].数学教育学报,2017,26(2):19-23.
[22] 李丹,张福娟,金瑜.儿童演绎推理特点再探——假言推理[J].心理科学,1985(1):6-12.
[23] GOSWAMI U. The Wiley-Blackwell handbook of childhood cognitive development [M]. 2nd ed. Malden, MA: Wiley-Blackwell, 2011:399-419.
[24] 吴明隆.问卷统计分析实务——SPSS操作与应用[M].重庆:重庆大学出版社,2010:208.
[25] 王光明,廖晶,黄倩,等.高中生数学学习策略调查问卷的编制[J].数学教育学报,2015,24(5):25-36.
[26] 焦彩珍,刘治宏.初中数学学习困难学生的抑制控制能力缺陷[J].数学教育学报,2018,27(1):47-51.
[27] 宋爽,郭衎.家庭背景因素对初中生数学学业成就的影响[J].数学教育学报,2018,27(1):52-57.
[28] 何忆捷,熊斌.中学数学中构造法解题的思维模式及教育价值[J].数学教育学报,2018,27(2):50-53.
[29] 陆明明.数学教科书例题的分类及其教学建议[J].数学教育学报,2018,27(2):54-58.
[30] 罗荔龄,曹广福.中学数学部分概率内容的问题与建议[J].数学教育学报,2018,27(2):65-69.
[31] 唐恒钧,HAZEL TAN,徐元根,等.基于问题链的中学数学有效教学研究——一项课例研究的启示[J].数学教育学报,2018,27(3):30-34.
[32] 刘春艳.理解试题内涵 把好教学方向——从一道北京中考试题说起[J].数学教育学报,2018,27(3):35-38.
[33] 卜文娟,温红博,刘先伟.初中学业水平考试中固定分数法标准设定的信度分析——以中考数学为例[J].数学教育学报,2018,27(3):39-44.
[34] 崔宝蕊,李健,王光明.初中生数学元认知水平调查问卷的设计与编制[J].数学教育学报,2018,27(3):45-51.
[35] 王红兵.针对初中毕业阶段学生范希尔几何思维水平的调查及其分析[J].数学教育学报,2018,27(3):52-56.
[36] 何小亚,李湖南,罗静.学生接受假设的认知困难与课程及教学对策[J].数学教育学报,2018,27(4):25-30.
[37] 张蜀青,曹广福,罗荔龄.从历史发展的视角看中学概率教学[J].数学教育学报,2018,27(4):35-40.
[38] 曹春艳,吕世虎.民国时期中学数学课程内容的发展历程及其启示[J].数学教育学报,2018,27(4):41-45.
[39] 关丹丹,景春丽.新高考改革背景下不分文理的数学成绩差异研究[J].数学教育学报,2018,27(4):31-34.
[40] 谷晓沛,马云鹏,朱立明.高一学生函数概念数学理解水平的实证研究——以T城市为例[J].数学教育学报,2018,27(3):25-29.
[41] 李渺,徐新斌,陆颖,等.高中数学教师听评课的现状及其有效性对策研究[J].数学教育学报,2018,27(1):36-41.
[42] 朱立明,胡洪强,马云鹏.数学核心素养的理解与生成路径——以高中数学课程为例[J].数学教育学报,2018,27(1):42-46.
附录:初中生逻辑推理测验
同学们好!下面是一些有趣的问题,请你完成解答.注意:除了1、2题可以多选外,其余各题都是单项选择.
学校年级性别
1.下列说法正确的是( ).(可多选)
A 所有的等边三角形都是等腰三角形 B 所有的等边三角形都不是等腰三角形
C 有些等边三角形是等腰三角形 D 有些等边三角形不是等腰三角形
2.初一(3)班有50名同学,其中有10名共青团员.下列说法正确的是( ).(可多选)
A 初一(3)班所有的同学都是共青团员 B 初一(3)班有些同学是共青团员
C 初一(3)班所有的同学都不是共青团员 D 初一(3)班有些同学不是共青团员
3.犯罪行为不是合法行为,故意杀人罪是犯罪行为.由此可以推出( ).
A 故意杀人罪不是合法行为 B 不合法行为是犯罪行为
C 不是犯罪行为一定合法 D 有的犯罪行为是合法行为
4.无理数是无限不循环小数,无限不循环小数是无限小数.故此我们可以推出( ).
A 无理数不是无限小数 B 无限小数是无理数
C 无理数是无限小数 D 无限小数不是无理数
5.一件事的情况或者是,或者是,也有可能既是又是.
(1)如果事情的情况是,那么事情的情况也是吗?( )
(2)如果事情的情况不是,那么事情的情况是吗?( )
A 肯定是B 肯定不是C 不确定是不是D 不会做
6.如果=,则2=2.下列选项正确的是( ).
A 如果≠,则2=2B 如果≠,则2≠2
C 如果2≠2,则≠D 如果2≠2,则=
7.如果两个长方形的长与宽分别相等,那么它们的面积相等;现在长方形与长方形的面积相等,则一定有( ).
A 它们的长与宽一定分别相等 B 它们的长与宽可能都不相等
C 它们的长一定相等 D 它们的宽一定相等
8.五一长假期间学校组织去爬山,或者去爬泰山,或者去爬黄山;也可以两座山都爬.
(1)如果五一期间同学们爬了泰山,那么爬黄山了吗?( )
(2)如果五一期间同学们没有爬泰山,那么爬黄山了吗?( )
A 肯定爬了 B 肯定没有爬
C 不能确定有没有爬 D 不会做
9.现有一个四边形,已知它要么是梯形,要么是平行四边形.
(1)若有两组对边相等,这个四边形( ).
(2)若至少有一组对边不相等,这个四边形( ).
A 肯定是梯形,不是平行四边形 B 肯定是平行四边形,不是梯形
C 有可能是梯形,也有可能是平行四边形 D 不会做
10.一件事的情况要么是,要么是,不可能既是又是.
(1)如果事情的情况是,那么事情的情况也是吗?( )
(2)如果事情的情况不是,那么事情的情况是吗?( )
A 肯定是B 肯定不是
C 不确定是不是D 不会做
11.如果两个自然数的乘积是奇数,那么他们的和是偶数.以下情况错误的是( ).
A 两个自然数的乘积是奇数,它们的和是偶数
B 两个自然数的乘积是奇数,它们的和是奇数
C 两个自然数的乘积是偶数,它们的和有可能是偶数
D 两个自然数的乘积是偶数,它们的和有可能是奇数
12.姚明不但参加过亚运会,而且参加过奥运会.这表明( ).
A 姚明参加过亚运会,可能参加了奥运会,也可能没参加
B 姚明参加了奥运会,可能参加了亚运会,也可能没参加
C 姚明参加过亚运会或奥运会
D 姚明两个都参加了
13.已知:一个四边形是矩形当且仅当四个角都是直角,那么以下情况正确的是( ).
A 一个四边形是矩形,它的四个角并非都是直角
B 一个四边形不是矩形,它的四个角都是直角
C 一个四边形不是矩形,它的四个角有可能都是直角
D 一个四边形不是矩形,它的四个角并非都是直角
14.公园里,小明指着湖面上的一群天鹅,说:“那些天鹅全部都是白色的.”小张仔细看了看,反对道:“不对,角落里有一只天鹅是黑色的.”以下说法正确的是( ).
A 只有一只黑天鹅,是个别情况,小明说的没错
B 有一只黑天鹅,说明小明的说法是错误的
C 黑天鹅只有一只,不能断定小明错了,除非能发现2、3只
D 黑天鹅只有一只,不能断定小明错了,除非一眼望去黑天鹅不比白天鹅少
15.小明说:“一个四边形,如果至少有两个角为90°,则它至少有一组对边平行.”为了证明小明的说法是错误的,需要找到一个四边形,满足( ).
A 只有一个角为90°,且有一组对边平行 B 没有90°的角,且有一组对边平行
C 有两个角为90°,两组对边都不平行 D 只有一个角为90°,两组对边都不平行
16.观察下列算式:21=2,22=4,23=8,24=16,25=32,……根据上述算式的规律,请你猜想22017的末位数字是( ).
A 2 B 4 C 6 D 8
17.我们知道,三角形是平面图形中边数最少的多边形.而在空间中,四面体(如图所示)是面数最少的多面体.这两者的性质之间有一些共通之处.根据三角形中任意两边之和大于第三边这一性质,可以推断在四面体中( ).

A 任意两个面的面积之和大于第三个面的面积
B 任意三个面的面积之和大于第四个面的面积
C 三个面的面积之和有可能等于第四个面的面积
D 三个面的面积之和有可能小于第四个面的面积
18.如果“杀人”对应“犯罪”,那么以下哪一组词的对应关系与此类似( ).
A 书法∶艺术 B 美丽∶漂亮 C 鲁迅∶周树人 D 历史∶通史
19.如图所示,按一定规律用火柴棍摆放图案:一层的图案用火柴棍2支,二层的图案用火柴棍7支,三层的图案用火柴棍15支,……,二十层的图案用火柴棍( )支.
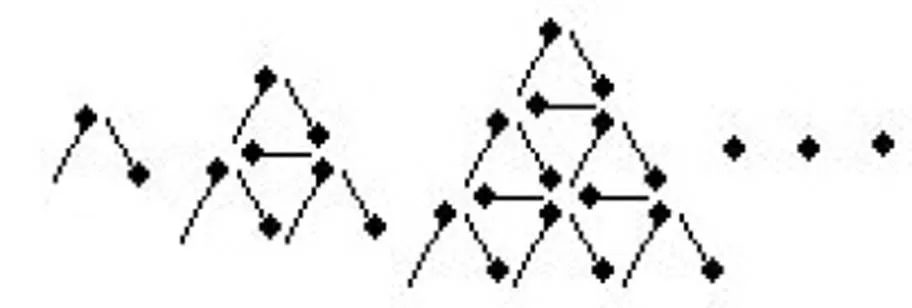
A 590 B 600
C 610 D 620
20.根据以下图中的凸多面体的面数、顶点数和棱数,以下结论中哪个是正确的( ).
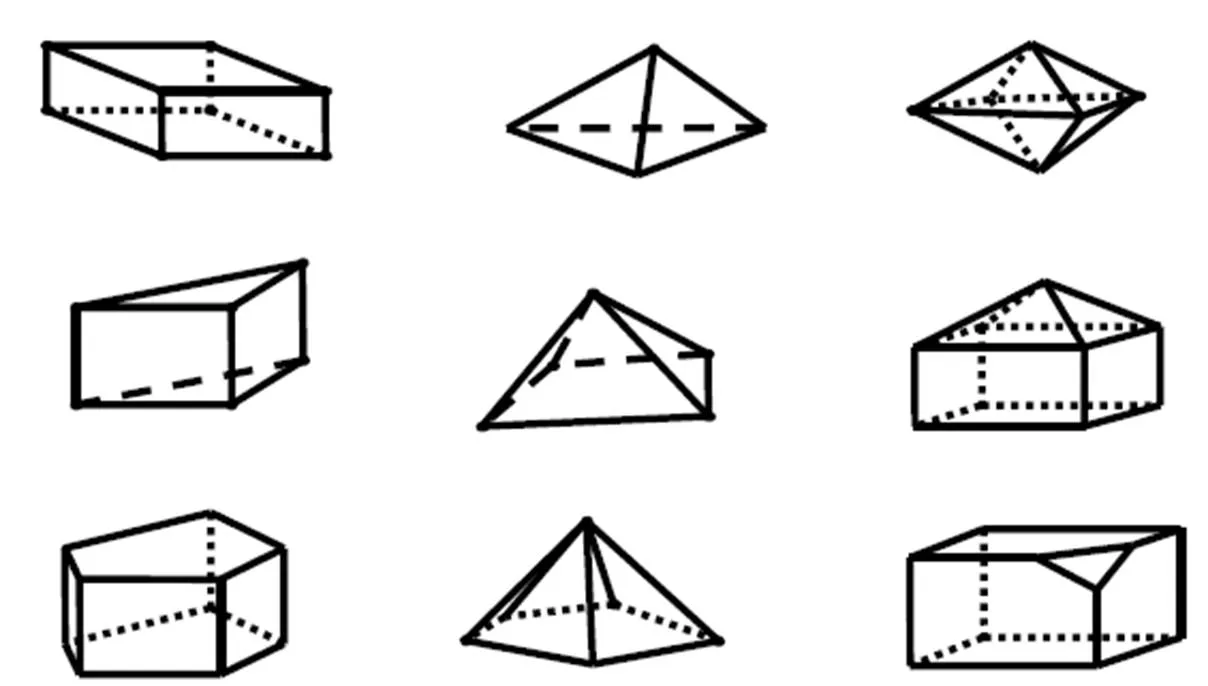
A 可以猜测+-=10 B 可以猜测+-=2
C 可以猜测+-=6 D 无法判断
21.如果有一组词是“寺庙—佛像—游客”,那么以下最为贴切的对应是( ).
A 商场—商品—营业员 B 画廊—展品—参观者
C 公园—城市—市民 D 学校—教室—考生
22.把1,3,6,10,15,21,……这些数叫做三角形数,这是因为这些数目的点子可以排成一个正三角形,那么第七个三角形数是( ).
A 25 B 26 C 27 D 28
Research on Test of Mathematical Reasoning of Junior High School Students
YAN Qing1, HUANG You-chu1,2, LUO Yu-hua3, CHEN Hao4, YU Ping1
(1. Institute of Curriculum and Teaching, Nanjing Normal University, Jiangsu Nanjing 210097, China;2. College of Education, Shanghai Normal University, Shanghai 200235, China;3. School of Education Science, Jiangsu Second Normal University, Jiangsu Nanjing 210013, China;4. School of Mathematical Sciences, East China Normal University, Shanghai 200241, China)
After a comprehensive analysis of existing literatures about mathematical reasoning, basing on classification of logic inference and research findings of reasoning ability in psychology, and also giving consideration to mathematical knowledge of junior high school, we proposed a framework which can be used to evaluate mathematical reasoning ability of junior high students, and designed a test. This test took into account both form and content of mathematical reasoning. With the result of exploratory factor analysis, we examined construct validity of the test and revised the test. The final dimensions were “plausible reasoning” and “deductive reasoning” which includes “simple proposition and inference”, “disjunctive inference”, “propositional calculus”, “hypothetical inference”. The test was good in construct validity and reliability.
mathematical reasoning; mathematical proposition; key competencies
G632.0
A
1004–9894(2018)05–0025–08
严卿,黄友初,罗玉华,等.初中生逻辑推理的测验研究[J].数学教育学报,2018,27(5):25-32.
2018–09–20
国家社会科学基金教育学一般项目——中学生学科核心素养的评价研究(BHA170150)
严卿(1987—),男,湖北武汉人,博士研究生,主要从事数学课程与教学论研究.
[责任编校:陈汉君、陈隽]

