JUMP Math项目的教学特色探讨及启示——基于化解数学教学难点的视角

何 岳，童 莉



JUMP Math项目的教学特色探讨及启示——基于化解数学教学难点的视角

何 岳，童 莉

（重庆师范大学 数学科学学院，重庆 401331）

有效化解数学教学难点，是数学课堂教学取得成功的关键．数学教育项目JUMP Math将复杂抽象的数学问题分解为若干步骤，并以“引导发现式”的教学模式激发学生的学习潜能和兴趣，成效卓越，获得2016年WISE教育项目奖．该项目在化解数学教学难点上的成功经验，对中国数学基础教育有着重要的启示作用．

数学教学难点；JUMP Math；教学设计

数学知识相对于其它学科具有一定的抽象性[1]，所以不管是在小学还是中学阶段，学生学习数学知识时容易产生恐惧心理[2]．因此，教师如何有效地化解数学教学中的难点，对于学生数学学习的好坏，激发和保持学生学习数学的热情，就显得至关重要．加拿大数学教师约翰·米顿（John Mighton）博士从学生切身情况出发，基于最新认知学领域的研究成果，并借鉴循证的教育理论（基于证据的教育理论）[3–4]，组建数学教育项目JUMP Math．该项目将数学难点适当分解，并采用“引导发现式”的教学模式[5]，激发了学生数学学习的热情，保证了教学效果．JUMP Math因其对数学基础教育的贡献和创新性获得2016年世界教育创新峰会（World Innovation Summit for Education，简称WISE）教育项目奖[6]．

这里深入探究JUMP Math的课程设置和教学案例，发现其在化解数学教学难点上的成功经验对中国数学基础教育有着重要的启示作用．如图1所示，该项目恰当运用循证方法[3–4]，创造性地将体艺类教学常用的分解教学思想运用于数学教学[3]，并采用框架化理论[7]，寻求既贴近学生生活又能揭示数学本质的情境，以“引导发现式”的教学模式[5]，帮助学生逐步突破学习障碍，建立学习信心．同时配合持续性评估和反馈，及时调整教学方案，缩小不同学生间的学习成果差距[8]．

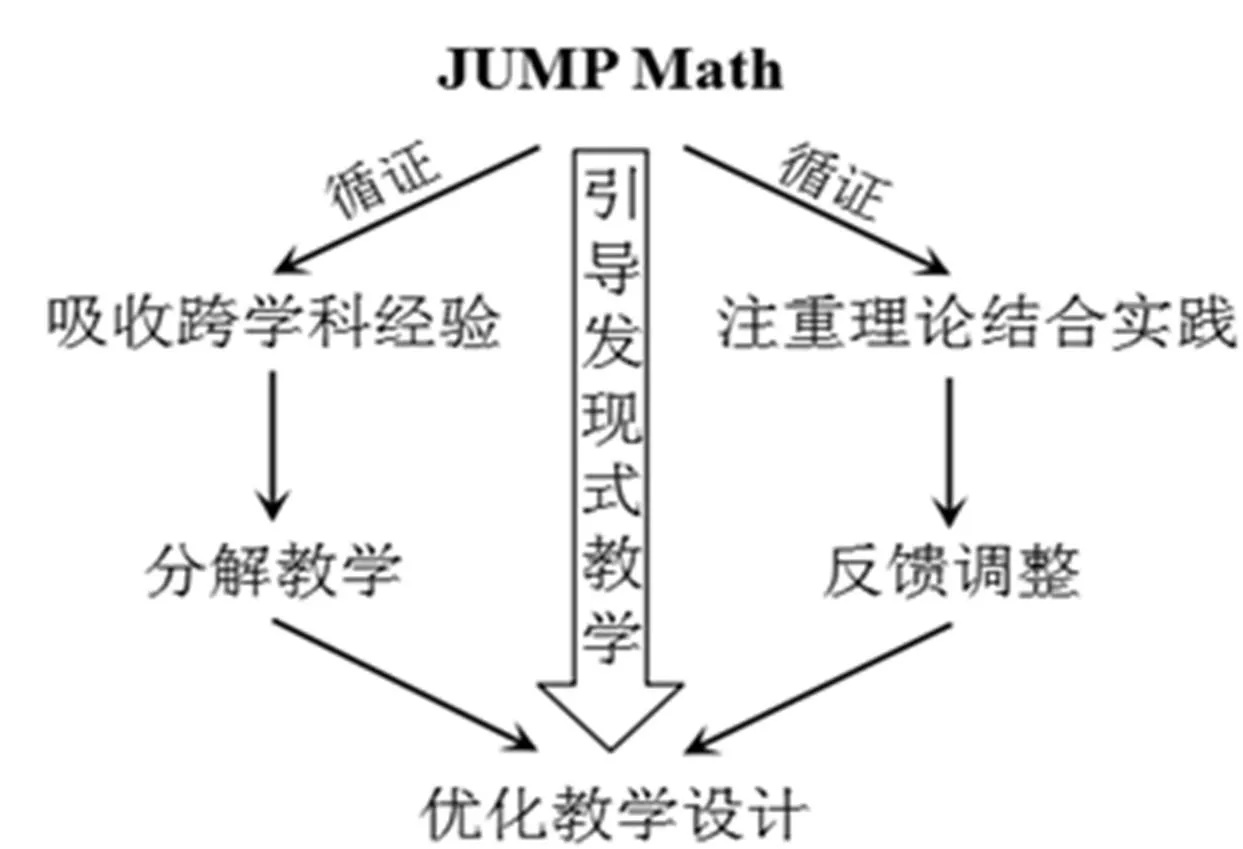
图1 JUMP Math化解数学教学难点的思路

1 JUMP Math项目简介

1.1 JUMP Math项目的起源和核心观点

为了让学生改变对于数学学习的恐惧和厌烦态度，增强学生的获得感和学习的愉悦感，1998年约翰·米顿从多年教学经验和实际案例出发，运用最新的循证教育理论，开发、设计了一套数学学习方法和课程，命名为“JUMP Math”．在字面上有“飞跃”的意思，但其实质为“Junior Undiscovered Math Prodigies”（未被挖掘的青少年数学天才），所以JUMP Math是一个起源于加拿大安大略省，旨在开发学生数学潜能的非盈利教育项目[9]．

该项目的核心观点是：绝大多数学生的智力水平基本相当，不会出现较大的差异．通过适当的教学方式，可以使每个学生学好数学，既收获数学知识亦得到思维的良好训练，并在将来的学习和生活中更好地发挥自身潜力，拥有更多的人生机会[10]．

1.2 JUMP Math项目的理论基础

JUMP Math项目的理论是建立在“循证教育”基础上的[3]．1996年，剑桥大学教授戴维·哈格里夫斯（David Hargreaves）在给一个教师培训机构做演讲时，首次提出了“基于证据的教育”这一说法．随后，“循证教育”逐渐应用到了教育领域，并为教育实践和教育理论之间关系的争议提供了一些解决方式．“循证教育”就是在教育教学的具体实践过程中，实现专业智慧和最佳可用经验证据的融合，其中跨学科性和理论与实践的互动是循证教育方法论的最主要体现[11]．

JUMP Math数学教育项目借鉴循证方法[3–4]，基于数学教学的专业智慧，从两个方面进行经验证据的整合．其一，跨学科、跨领域吸收有价值的经验和理论．分解教学通常用于体艺类教学，但该项目主动吸收其教学方式中的优点用以化解数学教学难点[3]．其二，注重理论与实践互动．该项目采用框架化理论（即人们倾向于按照自己的认知框架去体验现实，并根据这种框架采取行动，从而建构现实）[7]，寻求最佳数学素材，并在实际教学过程中，通过最佳可知可感且与数学知识高度匹配的情境实施“引导发现式”教学[5]，并注重根据教学反馈来调整教学方式．

1.3 JUMP Math项目在实际教学中的效果

JUMP Math起源于加拿大，随后在美国、西班牙和保加利亚也得到较好的发展．同时，美国教育部也特意拨款给一些大学及科研院校在40个班级里进行教学实验，希望真的能出现“飞跃”的结果[12–14]．截至2015—2016学年，约十七万名学生使用JUMP Math方案学习数学[15]，且在实际教学中取得了较好的教学效果．如在加拿大的一项随机对照测验中，使用JUMP Math的学生比使用普遍学习法的学生进度快了两倍．JUMP Math也在经济欠发达地区免费实施，在2012—2015年中每年的WRAT-4测试（Wide Range Achievement Test 4，包含识字、句子理解、拼写、数学运算）显示，这些地区随机选取的学生考试成绩都提高了1.8~2.9倍[16]．

2 JUMP Math化解教学难点的特色分析

JUMP Math致力优化数学课程方案和教学方法，以期能让学生克服数学学习困难，帮助教师更好地完成教学任务．因此，如何有效地化解数学教学难点，在该项目中具有重要的地位和作用．下面以JUMP Math中整数除法的教学为例[9]，介绍该项目在教学设计上的三大特色．

2.1 从学生切实的学习困难出发适当分解数学教学难点

JUMP Math从学生角度出发，依托大量认知心理学的研究成果[17–19]，实证调研影响学生数学学习的阻碍因素[8]，发现数学知识的抽象性是影响学生数学学习兴趣和热情的主要因素．因此，该项目在保持数学知识结构完整性和连贯性的基础上，适当将数学难点分解为若干教学环节，在每个环节的教学过程中，累积学生学习的成就感，增强了学生学习数学的信心和热情[20]．

比如在小学整数除法的教学中[9]，学生对于这一节的学习和掌握有3个难点．第一个难点就是“分”，要将本来作为一个整体的数分成高一级单位和低一级单位．第二个难点就是“换”，需要理解“换”的原因和方法，即当高级单位无法除尽时，将其“破坏掉”，转换成低一级单位的数便可以继续进行运算，并且在十进制计数法中，高一级的单位是低一级单位的十倍．第三个难点就是“通”，在对上述例题的学习和探究之后，需要学生在脑海中，形成一个完整的整式除法计算过程，掌握竖式计算的方法，做到触类旁“通”．针对以上学生学习的困难，将JUMP Math对整数除法教学的分解归纳为以下3个主要步骤（见图2）：

图2 JUMP Math对整数除法教学的分解

2.2 从学生思维训练角度出发增进学生对数学难点的理解能力

数学教学难点的外因是数学本身，内因则是学生主体的理解和认知能力．JUMP Math借鉴框架化理论，精选数学情境，组织数学活动[7，20]．该项目从学生身边最贴近、最可感知的现实情境入手，采取引导发现的教学模式，启发学生去思考问题、解决问题，提炼和掌握数学知识，实现知识学习和能力培养并重．下面介绍JUMP Math在整数除法教学中的具体过程[9]．

2.2.1 “分”的教学过程

JUMP Math在整数除法内容分解后，根据其特点，将72除以3的运算以如下情境引出：3个好朋友如何最公平地均分7角2分钱[9]．接着提出这样的问题：“同学们可以画图展示一下如何分配吗？”进而引导学生用X代替一角钱（鼓励学生有自己的表示方式），画出如图3所示的图形．在这一过程中，让学生体会到：要将7角2分钱均分3份，首先需要将7角均分．即将72这个数拆分成两部分：7角和2分．

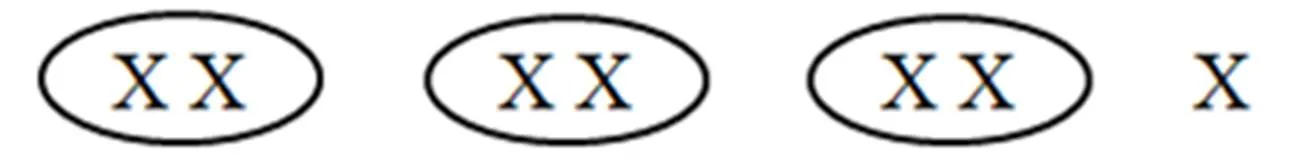
图3 整角均分的教学示例

2.2.2 “换”的教学过程

然后适当放手，给孩子们充足的思考与讨论时间，让他们自己探索如何将剩下的1角2分钱分成3份[9]．教师应该成为教学的积极组织者，让学生以小组为单位，提出解决问题的方法，并在这一过程中让学生感受为什么要将高一级单位换成低一级单位，还要对应理解各个数字在竖式中的涵义，如图4所示．

图4 整数除法的竖式计算过程和情节意义

2.2.3 “通”的教学过程

在新知识学习之后，教师引导学生回顾整理整数除法的过程，提炼整数除法的方法．再辅以变式训练（如教师给出“3个朋友分5角4分钱”），让学生进一步熟悉刚刚所学的知识，实现知识学习和实践运用的结合，形成贯“通”的知识体系，内化整数除法的通用方法和流程，如图5所示．

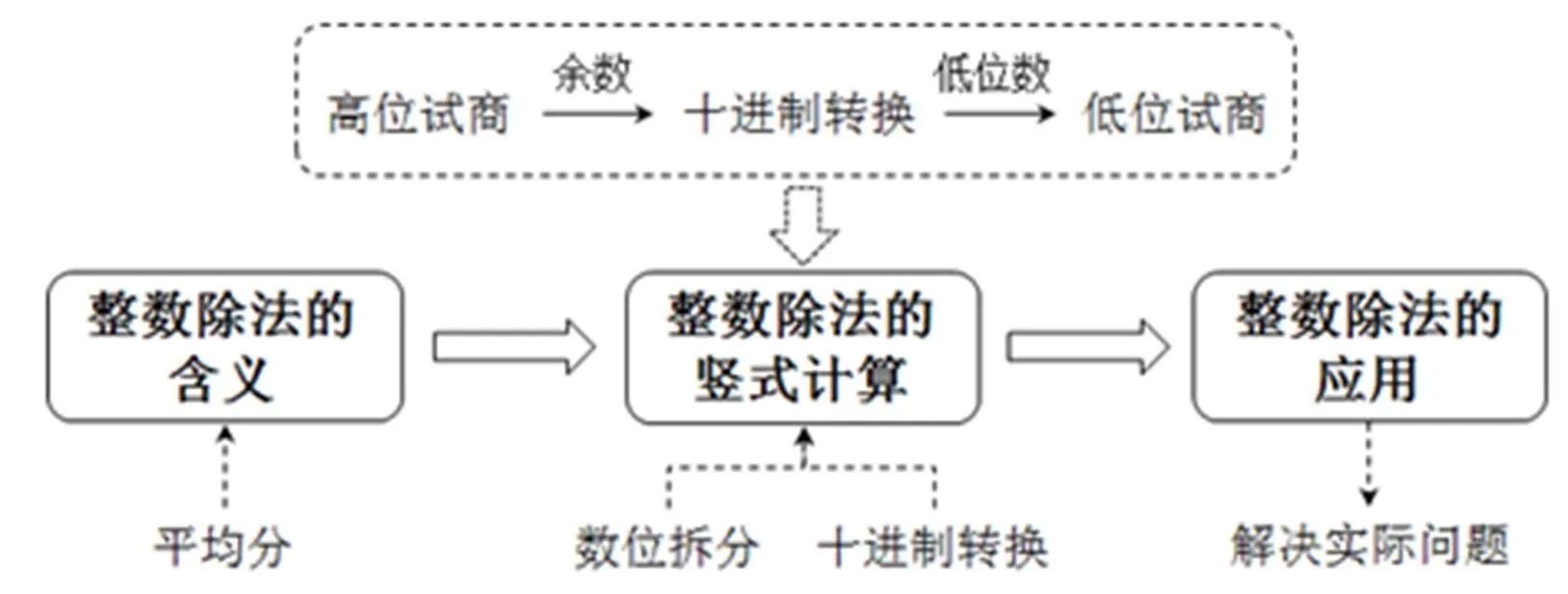
图5 整数除法的通用方法和流程

2.3 从学生反馈出发重视数学难点的实际教学效果

在具体教学的过程中，课堂教学不仅具有一定的预设性，也存在一定的生成性．所以在实际的教学过程中，教师需要时刻观察学生的状态，并在分解教学的基础上，持续进行评估和练习，从情境问题、变式练习、小组互动等多角度考察学生理解和掌握的情况[21]．例如在上述整数除法的教学案例中，JUMP Math设置的问题情境为“3个朋友分7角2分钱”，那么教师可以通过“如何均分整角”的问题了解学生对于整数拆分和高位向低位转换的理解程度，并积极从学生角度出发，解决学生的学习困难．这样，情境引入的作用就不仅仅是引起学生兴趣，同时也在情境互动问答中，让教师可以及时了解学生的学习情况，灵活调整教学进度和方法．

3 JUMP Math项目对化解数学教学难点的启示

从JUMP Math在化解数学教学难点上的成功经验，并与人民教育出版社官网上提供的教学参考（以下简称“人教参”）作对比[22]，可以得到化解数学教学难点的新思路．如图6所示，首先在已有教学经验的基础上，对数学教学难点适当分解，然后以“引导发现式”的教学模式开展教学，并在教学过程中注重对教学效果的检测反馈，再利用反馈信息及时调整教学设计和教学方式．

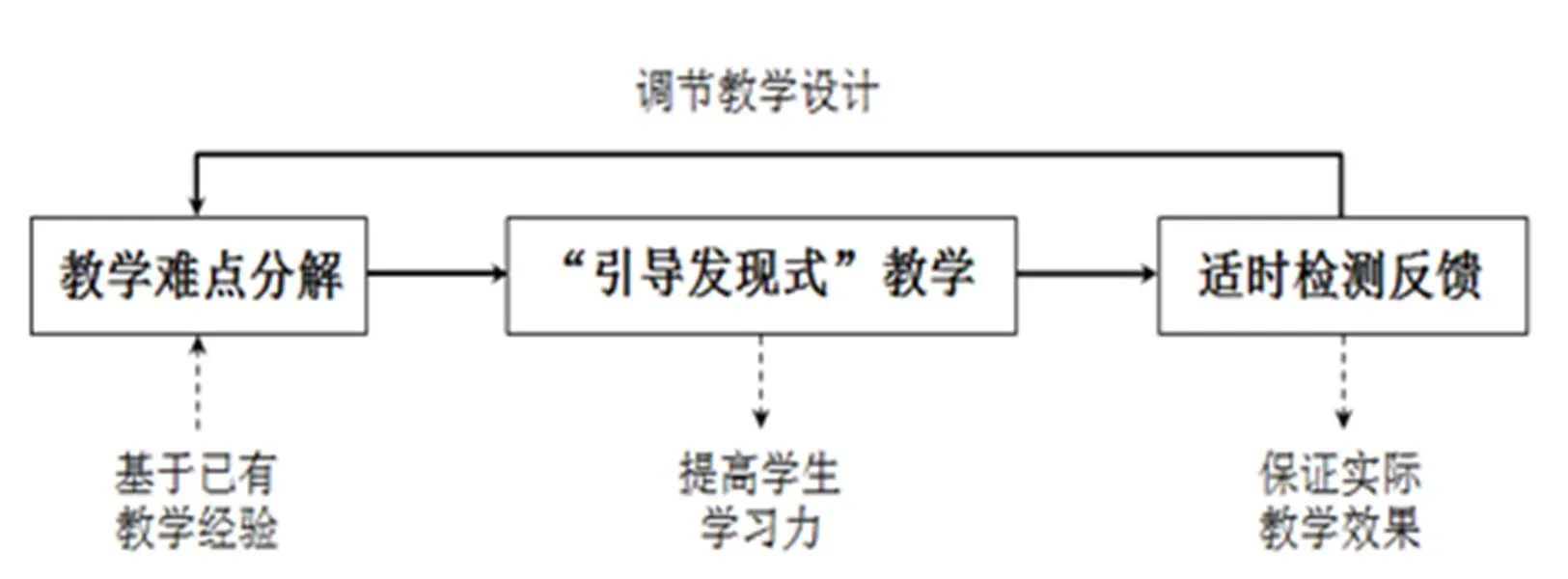
图6 化解数学教学难点新思路

3.1 教学难点分解 维护学生数学学习的热情

兴趣和信心是学生学习的内在动力，但是数学知识高度的抽象性和过大的思维跨度，一直以来在消磨学生的学习热情[2]．以整数除法为例，“人教参”中利用的是除法和乘法的互逆性，从简单除法的口算开始教学，侧重数学知识的内在逻辑[22]．而JUMP Math从学生学习的实际困难出发，在保持整数除法知识结构完整性和连贯性的基础上，将整数除法分解为“分—换—通”3个教学环节，并组织学生自我探索发现每一步的解决办法，提炼整数除法的方法，增强学生在每一环节的获得感．从这种教学设计思路得到启示：应该将教学内容始终放在学生知识的最近发展区，“爬楼梯”式地提高学生的数学知识和思维能力，避免某一环节的台阶过高给学生学习造成困难，进而产生对数学的厌学情绪．在2018年全国数学教育教学改革与发展研讨会暨数学教育博（硕）士生论坛上，美国德克萨斯A&M大学李业平教授做题为的汇报，也重点提到对于数学难点要划分结构，逐步分解，帮助学生有效掌握数学知识和技巧[23]．

3.2 “引导发现式”教学 提高学生对数学难点的学习力

随着教育的发展，当代教育更加重视培养学生的认知能力，重视在学习过程中，带领学生主动探索发现[24]，这已经成为大家认可的一种教育价值主张．“人教参”的教学设计虽然注重启发教学，却在“发现”教学上表现乏力．其在整数除法中使用的情境“52棵树，两班各需植树多少棵？”能启发学生理解整数除法竖式计算的涵义[22]，但JUMP Math项目中“3个朋友分7角2分钱”的例子更能帮助学生理解整数除法竖式计算中的难点．比如“角”和“分”很自然地帮助学生理解72是由7和2两部分组成；角与分的换算关系，也能辅助学生理解十位余数“1”如何转换到个位．JUMP Math从约翰·米顿自身学习经历和框架理论得到启发[7]，精选出既贴近学生生活又能揭示数学知识的情境，并以该情境辅助整个教学过程．学生在情境中完成对现实问题的逐步解答，提炼发现抽象的数学知识．这样适度“放手”的教学模式[25]，可以有效激发学生的学习动力，锻炼学习毅力，提高学生自身的学习能力．也只有学生自身的学习力（学习动力、学习毅力和学习能力）得到提高，才能更好地理解和掌握数学难点[26]．

3.3 适时检测反馈 保障化解教学难点的实际效果

理论需要实践的检验，在教学过程中也是这样．在具体教学中，及时检测教学的效果，发现存在的问题，尤其是难点教学问题．教师要主动适应学生学习的速度，调整教学的进度和方式，保证学生能在掌握前一阶段知识的基础上，开始下一阶段的学习[27]．在“人教参”中对于习题的设计和要求比较重视[22]，但仅仅依赖习题反馈的模式，不能使学生学习的困难得到充分解决，这也造成课外培训班和补习机构的盛行．根据多个实证研究表明，学生课外补习以提高成绩为主要目的[28–30]，这也间接说明学生在学校学习过程中的数学问题没有得到足够的重视和解决．JUMP Math利用及时反馈和有效实例，保持持续性评估和练习，促进更多学生跟上教学进度．这也启发教师要积极转变角色，不能以自我为中心，而是要主动适应学生群体，灵活调整教学设计和安排[31–35]，要把“以学生为主体”的教育思想落实到具体的课堂教学中，最大限度保证每个学生不掉队．

4 结语

JUMP Math数学教育项目中教学设计的最大特色就是充分尊重了学生的主体需要，体现了以人为本的教育观．该项目积极分解教学难点，重视启发学生思维，及时客观地检测学生的学习效果，帮助学生克服数学学习困难，维持和提高了学生的学习兴趣．同时，这也启示中国数学教育工作者，应该转变思维，充分尊重和服务学生的学习需求，在实践的基础上多角度地探索和创新化解教学难点的方式方法，让每个学生都能感受数学的魅力，爱上数学．

[1] 巩子坤．数学知识的特征与学习方式的有效选择[J]．中国教育学刊，2005（11）：55–58．

[2] 张景中．从数学难学谈起[J]．世界科技研究与发展，1996（2）：20–29．

[3] MIGHTON J. The end of ignorance: multiplying our human potential [M]. Canada: Vintage Canada, 2008: 1–13.

[4] JUMP Math Canada. Every child can learn math and love it [EB/OL]. (2017–01–01) [2018–05–21]. https://jumpmath. org/jump/en.

[5] KUDLA S. A little about JUMP [J]. Canadian Mathematical Society (CMS), 2012 (8): 4–5.

[6] 李刚．世界教育创新峰会（WISE）教育项目奖（2009—2016）的多元分析及启示[J]．外国中小学教育，2017（9）：1–4．

[7] KIRSHNER D. Review: and all the children are above average: a review of “the end of ignorance: multiplying our human potential” [J]. Journal for Research in Mathematics Education, 2010, 41 (1): 81–87.

[8] JUMP Math Canada. Supporting research [EB/OL]. (2011–01–01) [2018–06–20]. https://jumpmath.org/jump/en/supporting_ research.

[9] MIGHTON J. JUMP Math: mutiplying potential [J]. Notices of the AMS, 2014, 61 (2): 144–145.

[10]  JUMP Math Canada. Philosophy [EB/OL]. (2016–01–01) [2018–06–20]. https://jumpmath.org/jump/en/philosophy.

[11] 徐文彬．循证教育的方法论考察[J]．教育研究与实验，2014（4）：3–5．

[12]  BORNSTEIN D. A better way to teach math [J]. The New York Times, 2011, 4 (18): 1–3.

[13]  BORNSTEIN D. When math makes sense (to everyone) [J]. The New York Times, 2011, 4 (24): 1–2.

[14] JUMP Math Canada. JUMP Math global [EB/OL]. (2016–01–01) [2018–06–20]. https://jumpmath.org/jump/jump_ global/.

[15] LAMMERS-HELPS H. Build your kids’ math skills [EB/OL]. (2016–03–01) [2018–06–20]. https://www.country- guide.ca/2016/11/03/tips-to-build-your-kids-math-skills-country-guide/49776/.

[16]JUMP Math Canada. JUMP Math research [EB/OL]. (2016–06–01) [2018–07–20]. https://jumpmath.org/jump/us/ research.

[17]  POSNER M R. Influencing brain networks: implications for education [J]. TRENDS in Cognitive Science, 2005, 9 (3): 99.

[18]  GATHERCOLE S E, ALLOWAY T P, KIRKWOOD H J, et al. Attentional and executive function behaviours in children with poor working memory [J]. Learning and Individual Differences, 2008, 18 (2): 214–223.

[19]  SCHWARTZ J, BREGLEY S. The mind and the brain [M]. NY: Regan Books, 2002: 1–20.

[20]  MIGHTON J. The myth of ability [M]. Canada: St Martins Pr, 2004: 1–50.

[21]  ASHMAN G. Discovering Jump Math [EB/OL]. (2016–10–06) [2018–06–20]. https://gregashman.wordpress.com/2016/ 10/09/discovering-jump-math/.

[22] 人民教育出版社课程教材研究所．一位数除两位数[EB/OL]．（2010–01–01）[2018–06–20]．http://old.pep.com.cn/ xxsx/jszx/tbjxzy/jsys/xs3bjc/201008/t20100828_819784.htm．

[23] 胡睿．全国数学教育教学改革与发展的热点及趋势——2018年全国数学教育教学改革与发展研讨会暨数学教育博（硕）士生论坛综述[J]．数学教育学报，2018，27（4）：100–102．

[24] 杨恩彬．数学学习潜能的开发研究[D]．福州：福建师范大学，2008：13–15．

[25] 俞宏毓，朱向阳，顾泠沅．探究教学的设计与改进——以“面积与周长的关系”教学为例[J]．数学教育学报，2018，27（1）：68-71．

[26] 王欣瑜．基于学习心理结构的儿童数学学力测评观探析[J]．数学教育学报，2018，27（1）：62–67．

[27] 文晓宇．数学教学系统中的反馈和控制方法初探[J]．数学教育学报，2007，16（4）：63–66．

[28] 乔景香．小学生课外补习现状调查研究——以哈尔滨市A小学为例[D]．哈尔滨：哈尔滨师范大学，2017：20–22．

[29] 刘永秋．城市小学生课外补习的现状及对策——以北京市为例[D]．成都：四川师范大学，2014：27–29．

[30] 姚馨．小学生课外补习现状调查研究——以贵阳市某小学为例[D]．贵阳：贵州师范大学，2015：36–38．

[31] 郑毓信．数学教学的有效性与开放性[J]．课程·教材·教法，2007，27（7）：29–31．

[32] 庞雅丽．职前与在职小学数学教师HCK的比较研究[J]．数学教育学报，2018，27（1）：58-61．

[33] 何声清．六年级学生对高阶概率内容的认知：潜能与局限[J]．数学教育学报，2018，27（3）：57-61．

[34] 王宏，张守臣．小学生数学学业情绪问卷的修订[J]．数学教育学报，2018，27（3）：62-65．

[35] 裴昌根，宋乃庆，刘乔卉，等．数学学习兴趣测评指标体系的构建与验证[J]．数学教育学报，2018，27（2）：70–73．

Exploration and Enlightenment of the Teaching Characteristics in JUMP Math ——From the View of Solving Difficulties in Mathematics Teaching

HE Yue, TONG Li

(School of Mathematical Sciences, Chongqing Normal University, Chongqing 401331, China)

Solving the difficulties in mathematics teaching effectively was crucial to successful teaching. In the mathematical education project JUMP Math, the complex difficulties and abstract mathematical problems had been decomposed into several parts, and especially, the “Guided Discovery” teaching mode within it could stimulate students’ potential and interests in study. Thus, the educational fruit had been harvested remarkably, making JUMP Math win the prize of WISE Education Project Award in 2016. The successful experience in resolving the difficulties of mathematics teaching from the project had shed light on the basic mathematics education.

difficulties in mathematics teaching; JUMP Math; mathematics teaching design

2018–09–09

国家哲学社会科学基金2017年度教育学重点项目——教师核心素养和能力建设研究（AFA170008）

何岳（1989—），男，湖北孝感人，研究生，主要从事学科教学（数学）研究．童莉为本文通讯作者．

G421

A

1004–9894（2018）05–0048–04

何岳，童莉．JUMP Math项目的教学特色探讨及启示——基于化解数学教学难点的视角[J]．数学教育学报，2018，27（5）：48-51．

[责任编校：周学智、陈汉君]