解释的呈现方式对小学生数学样例学习的影响
杜雪娇,林洪新
解释的呈现方式对小学生数学样例学习的影响
杜雪娇1,林洪新2
(1.辽宁师范大学 心理学学院,辽宁 大连 116029;2.鲁东大学 教育科学学院,山东 烟台 264025)
在样例学习中提供多少解释,以及如何提供这些解释一直是广大研究者关注的问题.以六年级小学生为被试,设计了解释全部呈现,按照学生的需求呈现,按照学生对空缺处补写的正误呈现3种方式.比较了这3种方式在学习效率和效果上的差异.结果表明:与解释全部呈现相比,按需呈现方式缩短了样例学习时间,提高了规则应用效果,但没有提高规则迁移效果;而按正误呈现方式缩短了样例学习时间,同时提高了规则应用和迁移效果.故按照学生对空缺处补写的正误,提供符合学生水平的解释是一种较为有效且高效的方式.
样例;解释;呈现方式;小学生;计算机学习环境
1 问题提出
样例(worked example)通常包括待解决的问题,相应的步骤及最终结果[1].数学样例既可以是概念的例证,也可以是问题解决的例题以及规则、原理或公式的实例等[2].样例学习是人类习得认知技能和知识的重要途径[3].已有研究表明,样例学习能将学生有限的认知资源集中到与图式习得相关的认知活动上,相比于传统的问题解决练习,效果较好且效率较高[4].研究者已开发出了大量样例设计方法(如,多重变异样例[5],诱发自我解释样例[6]等)和呈现方式(如,渐减提示呈现方式[7],概念属性分步呈现方式[8]等),并验证了它们在不同学习内容和不同被试上的有效性.
而在样例学习过程中应何时给学生提供指导或解释,何时让学生独立地进行思考,以及应以何种方式提供这些解释一直是研究者所普遍关注的问题[9-10].一些研究者提出应在样例中添加指导性解释,所谓的指导性解释(instructional explanation)是指对样例中蕴含的原理所作出的解释[11].大量研究比较了有、无指导性解释样例的学习效果,但其研究结果不尽一致[12].一些研究表明指导性解释能帮助学生更好地理解样例,填补知识空缺,减少理解错误,提高学习效果[11].另一些研究则发现它对学习的促进作用并不理想[13].提供过多的解释会降低学生自主探究活动,且在学习过程中,随着学生知识水平不断地增长,一直提供详细的解释,可能会额外地消耗学生有限的认知资源来整合这些解释.此外,不同知识水平,领悟能力的学生往往需要不同详略程度的指导,对于初学者有效的解释,对于有一定背景知识或领悟能力的学生来说可能是无效的,甚至是冗余的[14].值得注意的是,在有的研究中指导性解释是一直呈现的,它直接添加在样例中.比如,在Richey和Nokes-Malach的研究中[9],无解释的样例仅呈现了相关解题步骤,而有解释的样例在其步骤旁边均给出了相关原理的详细解释.结果表明,在概念问题测验上无解释组被试的成绩显著高于有解释组被试的成绩.没有解释时学生可能更积极、主动地进行相关认知建构活动,故效果较好.而在有的研究中,指导性解释仅在学生需要时才呈现.比如在Renkl的研究中[11],有解释的样例只有当被试点击“解释”或“更多帮助”按钮后,才会呈现相应的解释或公式;而无解释的样例没有这些按钮及相应解释.结果表明,有解释组被试的学习效果显著优于无解释组被试.这里的解释是在学生进行主动思考并寻求帮助后才提供的.总之,已有研究仅比较了有、无指导性解释的样例学习效果,且在这些研究中解释的呈现方式存在差异,有的解释是一直全部呈现的,有的解释是按照学生的需求呈现的.让学生按照自己的需要,自主控制解释的呈现,可能会有效地避免信息冗余,激励学生在寻求解释之前,先主动地思考样例.故解释的呈现方式可能是影响其有效性的一个重要因素.目前尚没有研究直接比较解释全部呈现和按需呈现这两种呈现方式的学习效果,两者之间的差异有待进一步地实验验证.
此外,在样例呈现方式上,Renkl等人提出了渐减呈现方式[15].渐减样例(fading examples)即首先呈现完整样例,然后逐渐省略解题步骤,直至只剩下问题[16].它可以帮助学生从依靠学习样例逐渐过渡到独立解决问题[7].Kalyuga和Sweller开发了一个快速动态评估程序(rapid dynamic assessment of expertise)可用来实时追踪和评价学生的知识水平及其在学习过程中的变化情况[17].Salden等人以此程序作为呈现或省略相应解题步骤的依据[16],开发出了适应性渐减样例(adaptive fading examples).具体而言,这里的适应性渐减样例是根据快速动态评估系统的结果,也就是学生在相关问题上作答的正确率来决定呈现或省略解题步骤.如果该学生达到一定的正确率,则这一步骤被省略,以问题的形式呈现;如果没有达到这一正确率,则这一步骤仍直接给出,供其学习.结果表明,与以既定的顺序省略解题步骤的方式(固定渐减样例)相比,适应性渐减方式提供了与每个学生水平相匹配的个性化样例,提高了样例学习效果.同理可设想,在帮助学生理解领悟样例中所蕴含的规则时,可根据学生在相关问题上回答的正确率来决定是否呈现解释,这应该也会提高其学习效果.由前文可知,按需呈现解释时,学生需根据对自己学习情况的判断来决定是否寻求解释,这可能会受到学生对自身学习判断的准确性的影响.进一步,可按作答正误来提供解释,即由程序根据学生在相关问题上作答的正确率来判断其理解程度,并据此决定是否呈现相关解释.这种方式可能更能在恰当的时机提供适合每个学生水平的解释,故应设计按正误呈现解释的样例并验证其有效性.
在学习内容上,杜雪娇、张奇在研究中采用了“解释法”和“解释—标记法”设计“完全平方和”运算规则样例[18].所谓的“解释法”就是将新的运算规则或新算符用学生已知的运算规则或算符来加以数学解释,而“解释—标记法”在解释法的基础上用箭头标出运算步骤之间的对应关系.结果显示,学习“解释—标记法”样例的学生的远、近迁移测验成绩与学习解释法样例的学生的迁移成绩并无显著差异.即“解释—标记法”进一步促进效果不理想.无论是数学语言的解释,还是指明步骤间转化对应关系的标记解释,其本质均是一种指导性解释,用以帮助学生理解样例所蕴含的规则.如前文所述,不同领悟能力的被试学习可能需要不同程度的解释,且随着学习的深入,此前有效的解释也可能变得冗余.据此可推测,呈现过多的数学解释和标记解释可能会造成冗余,额外地消耗学生的认知资源,随着学习的深入反而会起到妨碍作用.因此,根据学生知识水平及其变化情况,提供适应性解释可能优于依次呈现所有解释的方式.故同样以完全平方和运算样例为实验材料,设计了按需呈现解释和按正误呈现解释两种适应性解释呈现方式,并与解释全部呈现方式进行对比,考察它们在样例学习效果和效率上的差异.
2 方法
2.1 被试
从潍坊市胜利东小学的六年级学生中随机选取100人,通过“前测”筛选出91名正式实验被试.其中女生45人,男生46人,平均年龄为11.96岁.将其随机分为3组,全部呈现组30人;按需呈现组30人;按正误呈现组31人.
2.2 实验设计
采用单因素被试间实验设计.自变量是解释的呈现方式,分为“全部呈现”“按需呈现”“按正误呈现”3种.因变量为样例学习时间,远、近迁移测验成绩及规则应用测验成绩.
2.3 实验材料
2.3.1 前测材料
前测材料包括6道题,前两道题是平方运算题,第三道题为乘法交换律测题,第四道题为分配律测题,它们包含了理解领悟完全平方和规则样例的基本知识.后两道题为完全平方和测题,即待学习内容.只有掌握了基本知识(正确计算出前4道题),且没有掌握待学习内容(不能正确计算出后两道题)的被试才能成为正式实验的被试.
2.3.2 样例学习程序
利用Sublime Text 3进行编写前端网页代码和Javascript代码,再借助浏览器呈现.分为3种程序,每种均包含两道样例,学生依次学习这两道样例.程序可自动记录每个学生所用的学习时间.其中,第一种样例学习程序中所有解释是依次呈现的(全部呈现样例);第二种学习程序中解释是学生按照自身需要选择呈现的(按需呈现样例);第三种学习程序中的解释是按照学生对空缺处补写的正误呈现的(按正误呈现样例).这3种样例学习程序除解释的呈现方式不同外,其余均相同.其中,完全平方和运算规则及所涉及的解释均与此前研究相同[18].
全部呈现样例即所有的算式解释和标记解释全部依次呈现,学生学完当前内容,点击“继续”按钮,继续学习,直至学完所有样例.在这种呈现方式下,所有解释均依次呈现,学生仅能通过点击“继续”按钮,控制学习进程.
按需呈现样例即样例的算式解释和标记解释是根据学生需要提供的,它们仅在学生寻求帮助时呈现.具体而言,程序首先呈现第一步,如果学生能直接看懂可点击“下一步”按钮,继续学习;如果学生没有看懂,则点击“?”按钮,查看这一步的算式解释,如果学生依旧没有看懂,可继续点击“?”按钮,查看这一步的标记解释.以此类推,直至学习完所有样例(见图1).
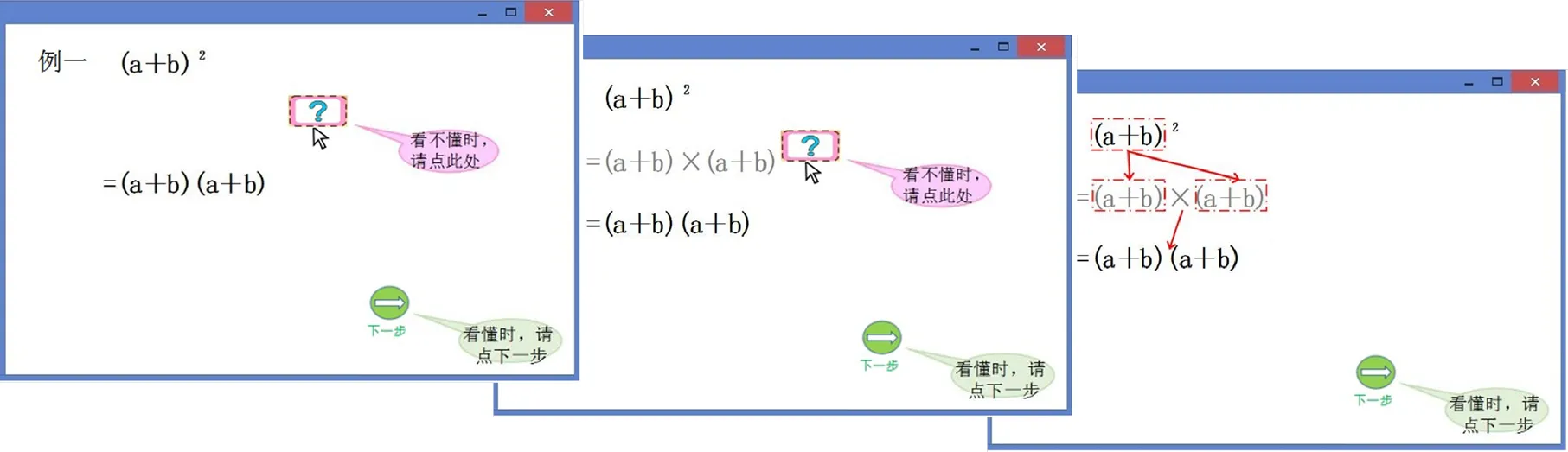
图1 按需呈现组样例截屏(第一步及学生点击“?”按钮后所呈现的解释)
按正误呈现样例即解释的呈现与否是由学生对空缺处填写的正误决定的,不是由学生自己选择的.具体而言,程序首先呈现第一步,该步骤有一个位置是空缺的,要求学生按照自己的理解补充完整.如果填写正确,则给出“对号”并继续呈现下一步;如果填写错误,呈现这一步的算式解释,要求学生在其帮助下填写,若学生再次填写错误,则呈现这一步的标记解释,同样要求学生在其帮助下填写,若学生依旧填写错误,则呈现正确答案.填写正确,会出现“对号”并自动呈现下一步,继续学习.以此类推,直至学习完所有样例(见图2).
2.3.3 测验材料
测验材料包括远、近迁移测验和规则应用测验,均由3道测题组成.近迁移测验与样例的表面特征不同,结构特征相同;远迁移测验与样例的表明和结构特征均不同.规则应用测验要求学生应用所学到的完全平方和知识,简便计算多位数相乘问题.被试做对1题记1分,远、近迁移测验及规则应用测验满分均为3分.

图2 按正误呈现组样例截屏(第一步及学生不能正确填写时所呈现的解释)
前测材料和测验材料分别在A4纸上呈现.样例学习材料在学生的计算机上呈现,计算机屏幕为17英寸,分辨率为1 024×768像素.
2.4 实验过程
2.4.1 前测阶段
向各组待选被试发放前测材料.前测时间为8分钟.选择能够正确做出前4道题,且不能正确计算出后两道题的被试进入下面的实验.
2.4.2 样例学习阶段
3组被试分别在不同的机房内同时进行学习.首先,给各组被试呈现相应学习程序的指导语.要求被试看明白后,输入姓名,点击“开始”按钮,开始学习.被试完成学习后,即可点击“结束学习”按钮,退出程序.学习时间最长为15分钟,若被试在15分钟内没有完成学习,也结束学习,时间计为15分钟.
2.4.3 测验阶段
给各组被试发放测验材料,测验时间为30分钟,到时间后,收回测试材料.
3 结果
利用SPSS19.0进行统计分析.各组被试所需学习时间及其在远、近迁移测验和规则应用测验中的成绩的平均数和标准差见表1.

表1 各组被试所需学习时间(秒)及其测验成绩(分)的平均数和标准差
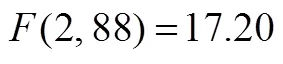
上述研究结果表明,按需呈现组被试在远、近迁移测验成绩上与全部呈现组被试的测验成绩无显著差异.仅在规则应用测验成绩上显著优于全部呈现组被试,且按需呈现组被试所需的样例学习时间明显少于全部呈现组被试所需时间.这表明与全部呈现解释相比,按需呈现解释对小学生学习完全平方和样例的迁移效果并没有明显的促进作用,但明显提高了其规则应用效果,节约了样例学习时间.按正误呈现组被试在远、近迁移测验和规则应用测验上的成绩均显著优于全部呈现组被试,且按正误呈现组被试所需的样例学习时间也明显少于全部呈现组被试所需时间.这说明与全部呈现解释相比,按正误呈现解释能提高完全平方和样例的迁移,规则应用效果且节约样例学习时间.
4 讨论
4.1 按需呈现解释对样例学习的影响
按需呈现解释时学生可根据自己的理解程度,选择查看相应的解释,这一方面可以促进学生积极地思考样例,另一方面可以避免因为提供过多的解释而造成信息冗余.按需呈现解释提高了该规则的应用效果,可能正是由于按需呈现解释的样例较为简洁,学生可以从整体上把握该规则,并应用其解决具体问题.与假设不尽一致,按需呈现组并没有提高该规则的迁移效果.究其原因可能是,按需呈现解释时,学生要正确地监控自己的学习过程,进行准确地学习判断,并在恰当时机主动寻求帮助.这时,学生对自己学习过程的监控和元认知水平就成为制约其学习效果的关键.当学生不能精确地监控其学习时,他们就不能有效地控制学习行为(比如,不能恰当地分配学习时间),进而影响学习效果[19].以往研究结果表明随着年级的增长,学生对自身学习监控的准确性逐步提高[20].而该研究采用的被试是小学生.他们可能尚不能精确地判断自己的理解情况,不能在恰当的时机寻求帮助.并且他们倾向于认为自己已经理解样例,不主动寻求解释帮助.故他们对样例的理解可能还不够深入,进而在需要进行灵活变式的迁移测验上没有显著优势.最后,按需呈现组被试所用样例学习时间较短.一方面按需呈现解释节省了整合冗余信息所需的心理努力和时间;另一方面如前文所述,六年级小学生往往高估自己的学习程度,没有深入理解样例就结束了学习,进而样例学习时间较短.未来研究可添加学习判断准确性[21]这一指标,并考察学生在学习判断上的准确性对按需呈现解释方式学习效果的影响.此外,按需呈现解释在高年级学生上的有效性也有待进一步探究.未来研究还需考察按需呈现解释方式在不同认知监控水平和元认知能力的学生上的有效性.
4.2 按正误呈现解释对样例学习的影响
按正误呈现解释克服了按需呈现解释方式中学生学习判断不准确的情况,显著提高了规则的迁移和应用效果,节约了样例学习时间.该结果与以往研究中适应性渐减样例好于固定渐减样例这一结果相一致[17],并将其扩展到解释的适应性呈现上.一方面按正误呈现解释避免了呈现过多解释所造成的信息冗余,降低了学生学习过程中所消耗的无效认知负荷.另一方面,该方式要求学生先主动思考样例,进行自我解释并补充空缺处.然后据此判断学生的理解情况,提供适应其知识水平的解释.即首先要求学生对空缺处进行自我解释,仅在学生不能进行正确的自我解释时,提供指导性解释.其中,补充空缺处也可以看作是一种自我解释提示,所谓的自我解释(Self-explanation)是指由自我产生并指向自我知识建构的认知活动[22].自我解释活动有助于知识的学习和迁移[6].按正误呈现解释有效地实现了学生的自我解释优先,指导性解释仅在学生需要时提供这一原则[11].该研究将Salden等人的适应性渐减样例的思想纳入到解释的适应性呈现上来[16],实现由依赖详细解释到独立理解样例的过渡.故未来的样例程序设计可以按照学生对相关问题作答的正误,决定是否呈现详细解释.而如何准确地设置这些问题并精确地判断学生知识水平的动态变化是设计按正误呈现解释样例的关键,也是未来研究的重点.
4.3 研究意义与教学建议
该研究设计、开发了按需呈现解释和按正误呈现解释两种解释呈现方式,验证了它们在样例学习中的有效性.其本质均为根据学生个体知识水平及其发展变化情况,提供与学生知识水平及其变化相适应的解释.总体而言,这两种解释的呈现方式均能帮助学生理解并领悟样例中所蕴含的规则,同时避免因提供过多解释而造成信息冗余.按正误呈现解释进一步避免了学生对自身学习判断不准确的现象,是一种有效且高效的方式.
期望这些结论可以应用于实际教学过程中,为例题学习程序的编制提供可借鉴的方法.首先,教师在设计样例或教学时,应该了解学生的背景知识水平,按照每个学生的水平提供个性化的指导.指导过多或者过少均不利于学生在有限的时间内有效地掌握学习内容.其次,解释、标记等指导性解释不能代替学生自己的知识构建活动.在样例设计和教学中,应先要求学生对学习内容进行自我解释,指导性解释仅在学生不能进行正确的自我解释时提供.做到不愤不启,不悱不发.最后,对于小学生来说,要求其对自己的理解情况进行准确判断并据此主动寻求解释帮助可能存在困难.由此,在样例学习程序的设计过程中,可要求学生补充样例的某一部分,据此判断其掌握情况,并提供相应指导.这种方式更有利于激发学生的学习兴趣与动机,培养学生的探究能力,同时避免冗余效应,降低无效的认知负荷.随着教学技术的发展,各种教学软件、学习程序、计算机辅助教学(CAI)设计被广泛地应用于教学中[23–27].在此背景下学习程序应能测评学生在学习过程中的理解和掌握情况,据此提供个性化指导.在调动学生的学习主动性的同时,发挥计算机辅助教学的优势.期望该研究的结果可以为样例程序设计者提供新思路.
5 结论
(1)与全部呈现相比,按需呈现解释仅提高了规则应用效果,节约了样例学习时间.
(2)与全部呈现相比,按正误呈现解释提高了样例学习远、近迁移效果及规则应用效果,节约了样例学习时间.对于六年级小学生来说,是一种最为有效的解释呈现方式.
[1] MEVARECH Z R, KRAMARSKI B. The effects of metacognitive training versus worked-out examples on students’ mathematical reasoning [J]. British Journal of Educational Psychology, 2003, 73 (4): 449–471.
[2] 马俊青.数学样例学习与学生数学知识形成关系的研究[J].数学教育学报,2009,18(4):68–70.
[3] RENKL A. Toward an instructionally oriented theory of example-based learning [J]. Cognitive Science, 2014, 38 (1): 1–37.
[4] ATKINSON R K, DERRY S J, RENKL A, et al. Learning from examples: instructional principles from the worked examples research [J]. Review of Educational Research, 2000, 70 (2): 181–214.
[5] 宁宁,喻平.多重变异性数学样例对迁移影响的初步研究[J].数学教育学报,2010,19(6):50–52.
[6] 连四清,曾辉.自我解释对等差数列概念和通项公式远近迁移的影响[J].数学教育学报,2011,20(2):23–25.
[7] 史月杰.样例的呈现方式对学生学习排列知识的影响的实验研究[J].数学教育学报,2014,23(2):69–72.
[8] 甘卫群,刘万伦.样例的概念属性呈现方式对初一学生分式概念学习的影响[J].数学教育学报,2015,24(6):68–72.
[9] RICHEY J E, NOKES-MALACH T J. How much is too much? Learning and motivation effects of adding instructional explanations to worked examples [J]. Learning and Instruction, 2013, 25 (3): 104–124.
[10] WITTWER J, RENKL A. How effective are instructional explanations in example-based learning? A meta-analytic review [J]. Educational Psychology Review, 2010, 22 (4): 393–409.
[11] RENKL A. Worked-out examples: instructional explanations support learning by self-explanations [J]. Learning and Instruction, 2002, 12 (5): 529–556.
[12] KOEDINGER K R, ALEVEN V. Exploring the assistance dilemma in experiments with cognitive tutors [J]. Educational Psychology Review, 2007, 19 (3): 239–264.
[13] GERJETS P, SCHEITER K, CATRAMBONE R. Can learning from molar and modular worked examples be enhanced by providing instructional explanations and prompting self-explanations [J]. Learning and Instruction, 2006, 16 (2): 104–121.
[14] KALYUGA S, AYRES P, CHANDLER P, et al. The expertise reversal effect [J]. Educational Psychologist, 2003, 38 (1): 23–31.
[15] RENKL A, ATKINSON R K, MAIER U H, et al. From example study to problem solving: smooth transitions help learning [J]. Journal of Experimental Education, 2002, 70 (4): 293–315.
[16] SALDEN R J C M, ALEVEN V, SCHWONKE R, et al. The expertise reversal effect and worked examples in tutored problem solving [J]. Instructional Science, 2010, 38 (3): 289–307.
[17] KALYUGA S, SWELLER J. Rapid dynamic assessment of expertise to improve the efficiency of adaptive e-learning [J]. Educational Technology Research & Development, 2005, 53 (3): 83–93.
[18] 杜雪娇,张奇.样例设计及呈现方式对学习代数运算规则的促进[J].心理学报,2016,48(11):1 445–1 454.
[19] MIHALCA L, MENGELKAMP C, SCHNOTZ W, et al. Completion problems can reduce the illusions of understanding in a computer-based learning environment on genetics [J]. Contemporary Educational Psychology, 2015 (41): 157–171.
[20] BRYCE D, WHITEBREAD D. The development of metacognitive skills: evidence from observational analysis of young children’s behavior during problem-solving [J]. Metacognition and Learning, 2012, 7 (3): 197–217.
[21] HOOGERHEIDE V, LOYENS S M M, VAN GOG T. Comparing the effects of worked examples and modeling examples on learning [J]. Computers in Human Behavior, 2014 (41): 80–91.
[22] CHO Y H, SANG E L. The role of co-explanation and self-explanation in learning from design examples of PowerPoint presentation slides [J]. Computers and Education, 2013, 69 (4): 400–407.
[23] 濮安山,赵延廷.中学数学课堂教学应用CAI的调查研究[J].数学教育学报,2010,19(3):39–41.
[24] 庞雅丽.职前与在职小学数学教师HCK的比较研究[J].数学教育学报,2018,27(1):58-61.
[25] 俞宏毓,朱向阳,顾泠沅.探究教学的设计与改进——以“面积与周长的关系”教学为例[J].数学教育学报,2018,27(1):68-71.
[26] 王欣瑜.基于学习心理结构的儿童数学学力测评观探析[J].数学教育学报,2018,27(1):62-67.
[27] 宋爽,郭衎.家庭背景因素对初中生数学学业成就的影响[J].数学教育学报,2018,27(1):52-57.
The Impact of Presentation Modes for Explanations on Pupils’ Mathematical Example-Based Learning
DU Xue-jiao1, LIN Hong-xin2
(1. College of Psychology, Liaoning Normal University, Liaoning Dalian 116029, China; 2. School of Educational Science, Ludong University, Shangdong Yantai, 264025, China)
With regard to example-based learning, the much-debated questions were how many explanations should be provided, and what the optimal mode should be used to present them in order to support the robust learning. Thus, 6th-grade pupils were chosen as participants, the worked examples were designed by three presentation modes: 1) all explanation was presented; 2) the explanation was presented as learners’ required 3) the explanation was presented only when pupils gave a wrong answer to certain gap. An experiment was carried out to compare the learning effects and efficiency of three presentation modes. The results revealed that: when compared with all presenting mode, presenting as required mode improved the applied effects with less leaning time, however no enhanced transfer effects were observed. When compared with all presenting mode, presenting on wrong mode also improved transfer with less learning time, meanwhile it the applied effects. Since it was the most effective and efficient mode, it was recommended to present explanations based on whether answers filled by pupils in the gaps were right or wrong.
worked example; explanation;presentation mode; pupil; computer-based learning environment
2018–04–28
教育部人文社会科学青年基金项目——解释法对小学生数学运算样例学习成绩与认知负荷的影响(15YJC190011)
杜雪娇(1990—),女,山东潍坊人,博士生,主要从事样例学习研究.
G442
A
1004–9894(2018)05–0052–05
杜雪娇,林洪新.解释的呈现方式对小学生数学样例学习的影响[J].数学教育学报,2018,27(5):52-56.
[责任编校:周学智、陈隽]

